无轴承永磁同步电机转子径向位移估算策略

张汉年，张涛

（1.南京信息职业技术学院电子信息学院，江苏 南京 210023；2.淮阴工学院自动化学院，江苏 淮安 223003）

无轴承永磁同步电机是无轴承（磁悬浮）技术在永磁型同步电机的突破性应用[1]，尤其是在高速应用领域，它提供了一种比传统机械轴承（或磁轴承）支承的永磁同步电机更具吸引力的解决方案。无轴承永磁同步电机将主动磁轴承和普通永磁同步电机各自功能集成于同一个定子单元[2]，实现了电机转子悬浮和转动的集成化协同运行，因此减小了电机体积，降低了系统复杂性和使用成本。无轴承永磁同步电机与普通永磁同步电机的关键区别在于其定子铁心中按照设计要求放置极对数差为1的两套绕组：悬浮绕组和转矩绕组。无轴承永磁同步电机依据永磁体转子结构的不同，可分为内置式、表贴式、交替极式、组合磁极式等类型[3-4]，但其控制策略基本相同。相比其他无轴承交流电机，如同步磁阻型、开关磁阻型、感应型等，无轴承永磁同步电机具备较高的效率和功率因数，在工业机器人、高洁净生物医学工程、高精度数控机床等高品质电力传动领域有着显著的优势。

无轴承永磁同步电机悬浮和转动同步运行得以有效控制的关键是引入转子径向位移负反馈，位移反馈系统构建的前提是转子径向振动位移量的准确测量。检测转子位移通常做法是在无轴承永磁同步电机端盖上加装4个高性能电涡流位移传感器，但由此带来一些问题：1）打破了电机原本紧凑坚固的本体结构；2）位移传感器检测系统复杂且价格昂贵；3）高温高湿等恶劣环境下位移传感器检测精度下降；4）位移传感器初期安装和后期维护难度较大等。无位移传感器系统去除了昂贵且复杂的位移传感器，只检测定子绕组侧电压、电流就能在线辨识位移信号进行转子位置闭环控制，将会给无轴承永磁同步电机悬浮系统设计、电机制造及推广应用带来诸多便捷。

当前无轴承永磁同步电机转子位移估算方法较多，主要有模型直接计算、参数状态估计、参数在线辨识等。在无轴承永磁同步电机的无位移传感器控制环节，不少文献提出了有效的转子位移估算方法。文献[5]通过辨识绕组磁链，利用绕组磁链方程直接计算转子位移，该方法完全依赖电机绕组电感、电阻等固有参数，位移估计的准确度不高。文献[6]建立了转子径向位移和悬浮绕组自感的线性方程，面向悬浮绕组施加高频信号并对产生的差分电压进行信号处理，获取位移信息，但高频差分电压信号的准确提取难度很大。文献[7]分析了电机悬浮和转矩两套绕组的互感特征，提出了加注电压信号于转矩绕组的转子位移观测法，但额外注入的高频信号增加了悬浮和转动控制之间的耦合性，悬浮系统控制的稳定性下降。文献[8]提出了一种MRAS（模型参考自适应）转子位移无传感器控制方法，但电机参考模型自身的准确性对位移辨识精度影响很大，负载大幅波动下的系统抗扰性变差。文献[9]将BP神经网络左逆位移检测法应用于无轴承永磁同步电机，但BP神经网络存在学习算法复杂、位移预测精度低、误差大等问题。

最小二乘法已成功应用于普通交流电机，用以解决定子电阻、电感以及转速等参数的在线辨识问题[10]，但其在无轴承电机中的应用却很少见到。文献[11]采用遗忘因子最小二乘法仅对内插式永磁型无轴承同步电机电感参数进行在线辨识，并未对无位移传感器控制进行研究。

本文针对一台表贴式无轴承永磁同步电机，综合普通最小二乘法和遗忘因子最小二乘法各自算法优点，引入混合加权最小二乘法对该电机转子径向位移进行辨识，所提算法的可行性在仿真及实验中得到了验证，实现了电机转子径向位移的有效估算。

1 最小二乘法转子位移估算原理

1.1 转子位移估算模型

本文研究的无轴承永磁同步电机定子中装配两套完全对称的三相绕组：2极悬浮绕组和4极转矩绕组。为便于建立电机的数学模型，需对无轴承永磁同步电机作理想化处理，如忽略非线性磁饱和因素影响等。电机悬浮运行过程中转子会偏离定子中心，电机两套绕组之间会产生同转子偏心位移成正比的互感。两相旋转坐标系下（d-q坐标）电机定子两套绕组的磁链方程为

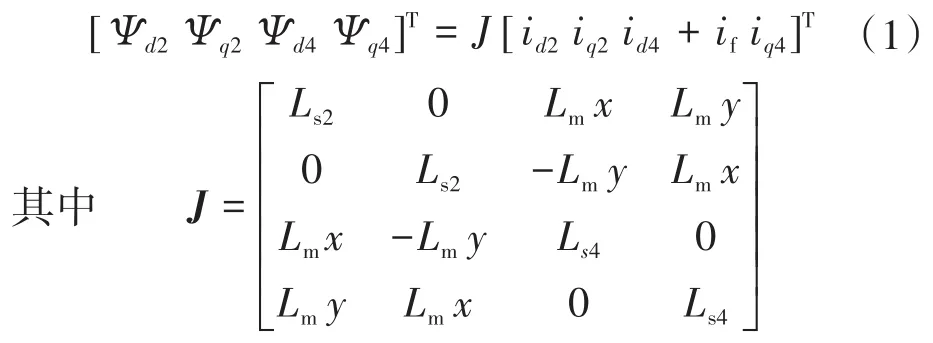
式中：Ψd2，Ψq2，Ψd4，Ψq4分别为悬浮绕组、转矩绕组定子磁链；id2，iq2，id4，iq4分别为悬浮绕组、转矩绕组定子电流；if为永磁体励磁电流；Ls2，Ls4分别为悬浮绕组和转矩绕组自感；Lm为悬浮绕组和转矩绕组之间互感系数，Lm与无轴承永磁同步电机两套绕组极对数、绕组串联匝数、悬浮绕组互感、定子铁心尺寸等参数有关[12]，由样机参数得到Lm估算值为0.722 Wb/m；x，y分别为d，q轴方向转子径向位移。

无轴承永磁同步电机的数学模型用微分方程（d-q坐标）可表示为

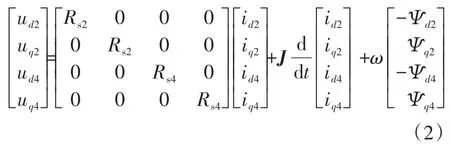
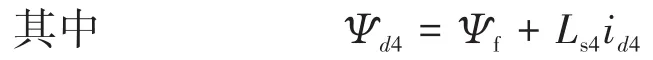
式中：Ψf为永磁体在转矩绕组中产生的磁链；ud2，uq2，ud4，uq4分别为悬浮绕组、转矩绕组定子电压；Rs2，Rs4分别为悬浮绕组、转矩绕组定子电阻；ω为转子角速度。

对式（2）进行变换，电机的状态方程可写为

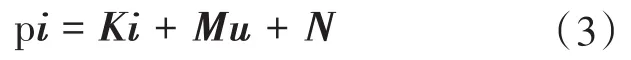
其中

式中：p为微分算子；K，M，N为系数矩阵。

对上述被控电机的微分方程式（3）进行离散化，可得下式：

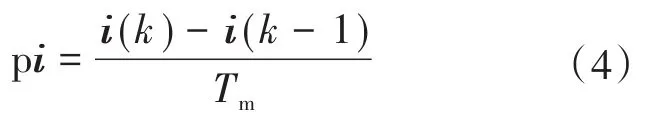
式中：i(k)，i(k-1)分别为i在k和（k-1）时刻采样值；Tm为采样周期。

令R=(Ι +TmK)，S=TmM，T=TmN，其中I为单位矩阵。进一步令矩阵Y(k)，θ(k)和φ(k)分别为

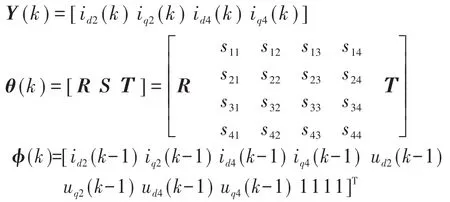
依据式（3）、式（4），系统的状态方程可进一步表示为

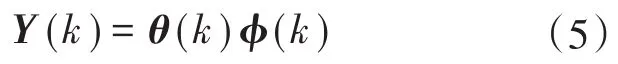
式中：Y(k)为输出量矩阵，表示将来时刻悬浮绕组和转矩绕组的电流值，无法经传感器直接测量获取；φ(k)为输入量矩阵，可以通过传感器检测电机悬浮绕组和转矩绕组电流、电压再经坐标变换获得；θ(k)为参数矩阵，由Y(k)和已测量出的φ(k)辨识得到。

综上可以发现，电机转子位移x，y及绕组自感参数Ls2，Ls4等包含在上述θ(k)的矩阵S中，选取合适的最小二乘算法便可辨识出S中的向量元素，进而间接计算得到转子位移及绕组自感等参数。无轴承永磁同步电机高速悬浮和旋转运行时，电机两套绕组自感和互感在受到外界温度、负载扰动和磁场饱和影响下会发生变化，电感参数的剧烈波动会影响转子位移的检测精度，降低了系统的悬浮性能。为提高无位移传感器下转子位移的估算精度，有必要同步辨识电机自感参数。

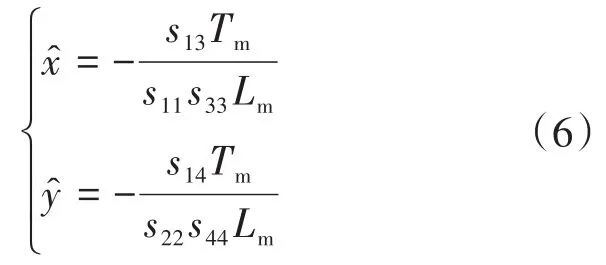
1.2 混合加权最小二乘转子位移辨识方法

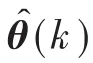
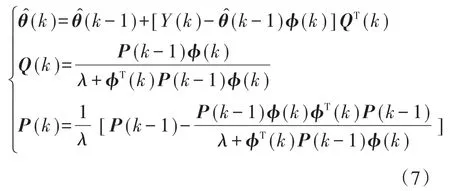
式中：λ为遗忘因子，用来表示参数观测过程中旧有辨识结果对当前辨识结果的影响。若λ=1，称为普通最小二乘法；若λ≠1（0＜ λ＜ 1），被称为遗忘因子最小二乘法[13]。普通最小二乘法对参数的观测能力较好，辨识结果较为稳定，但历史数据累积饱和后对参数的实时跟踪不够敏感，系统的收敛速度变得迟滞。带遗忘因子最小二乘法提高了参数观测的实时跟踪性能，但λ过小时数据观测值波动增大，参数辨识的精度下降。因此合理选择遗忘因子是决定最小二乘法参数估算性能和系统收敛速度的关键步骤，目前做法主要是依据经验，一般选取多个遗忘因子，分别经过对比实验，参考稳定性、收敛速度和辨识精度等各项指标，最终选择1个适中的遗忘因子。无轴承永磁同步电机转子位移等参数估算过程中，式（7）中矩阵Q(k)，P(k)快速衰减会降低其对参数辨识的修正能力，经反复调试，此处选取遗忘因子最小二乘法中的λ=0.665。

综合上述分析，为了使电机实际参数变化时悬浮系统观测结果波动小，且能及时跟随参数变化，本文对两种最小二乘法获取的转子位移误差信号进行加权处理，加权系数满足以下方程：

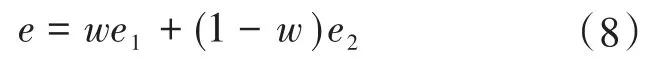
其中

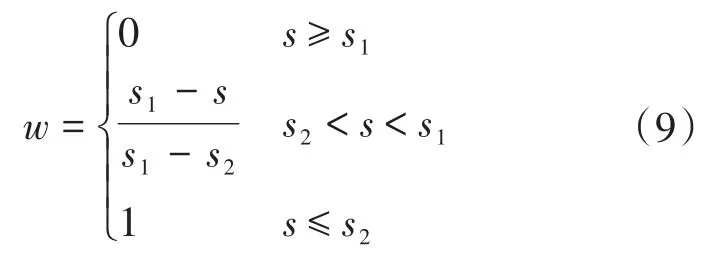
式中：e为加权转子位移误差信号；e1为普通最小二乘法得到的位移误差信号；e2为遗忘因子最小二乘法获取的位移误差信号；w为加权系数；s为转子实际径向位移；s1，s2为转子位移的上限值和下限值。

由式（9）可知，当电机转子初始启动或者受到负荷变动时，如实际径向位移大于s1，则w=0，此时转子位移误差信号仅取决于遗忘因子最小二乘法，由遗忘因子最小二乘法快速实现转子位移辨识。当电机转子位移波动趋于稳定后，其径向位移小于s2，则w=1，此时选用普通最小二乘法对转子位移误差信号进行控制，以进一步稳定位移辨识结果。当转子位移大小处于s1，s2之间时，转子位移误差信号由两种最小二乘法组合构成的加权方程决定。两种最小二乘法之间的切换是实现的难点，根据样机定、转子气隙大小，经多次调试，本文设定转子位移偏移量的上、下限值分别为s1=0.07 mm，s2=0.03 mm。

由式（4）～式（6）可看出，应用最小二乘法进行转子径向位移及电感参数辨识时，需要采集电机绕组电压、电流信号，此外还要获取不同时刻电流序列值，以便进行电流信号的一阶微分近似计算。由于电流、电压信号检测值含有谐波，因此有必要对位移及各电感参数的辨识值进行同步数字滤波处理。高阶巴特沃斯滤波器运算复杂，为使计算简单，此处选用低通滤波器（low pass filter，LPF），其结构形式为

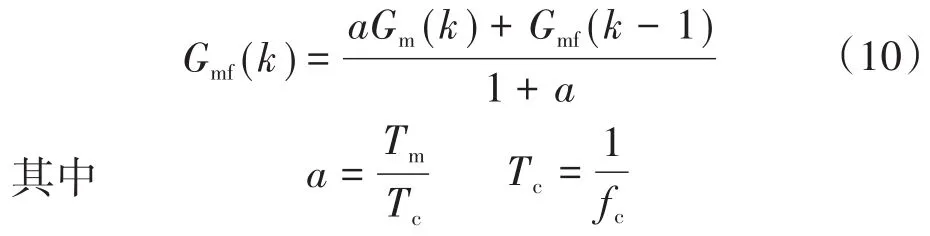
式中：Gmf(k)，Gmf(k-1)分别为k，k-1采样时刻转子位移及电感经滤波后的估算值；Gm(k)为k采样时刻转子位移及电感的估算值；fc为截止频率。文中向电机供电的SPWM逆变器载波频率设定为10 kHz，故采样周期可选用Tm=0.1 ms，此处低通滤波器截止频率设置为fc=100 Hz。

本文设计的混合加权最小二乘法位移估算器具体结构如图1所示。

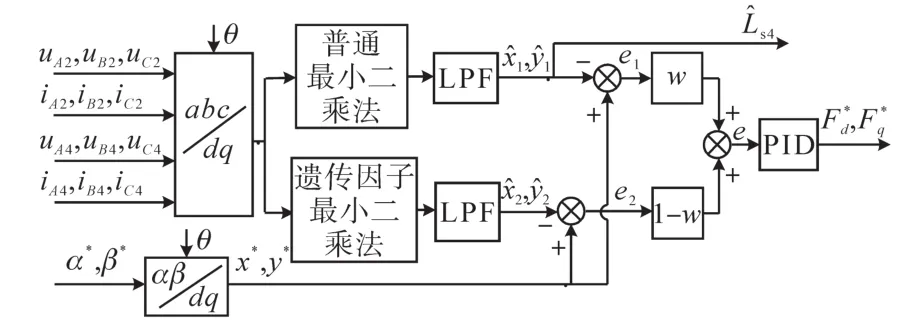
图1 混合加权最小二乘法位移估算结构图Fig.1 Structure diagram of displacement estimation with hybrid weighted least square method

2 电机转动与悬浮控制系统

无轴承永磁同步电机的转动控制主要包括转速调节和转矩控制，面向普通永磁同步电机的各种电力传动控制策略皆可适用于无轴承永磁同步电机。此处无轴承永磁同步电机转动控制采用基本的转矩绕组励磁电流id4=0控制（转子磁场定向），此时电机电磁转矩和转速方程为

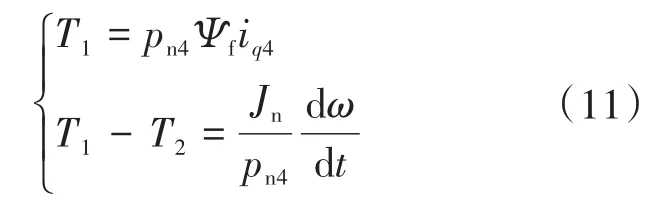
式中：pn4为电机转矩绕组极对数；T1为电磁转矩；T2为负载转矩；Jn为转动惯量。

两相旋转坐标下（d-q坐标），不考虑转子在径向所受扰动，仅计及转子偏离定子中心时在d，q轴所受的单边磁拉力Fd0，Fq0，电机稳定悬浮与转动下转子的牛顿力学模型为

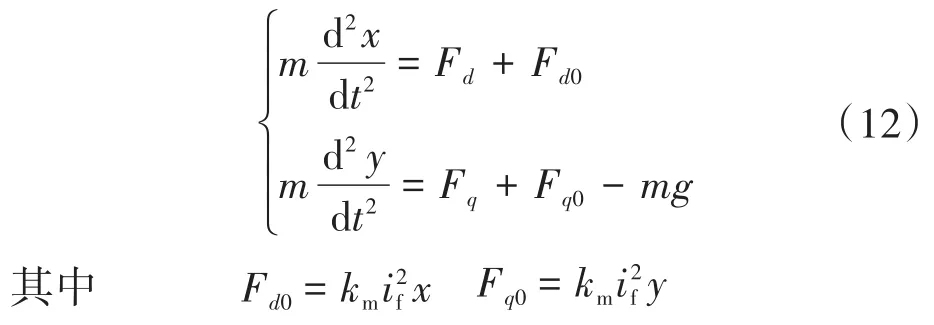
式中：m为转子质量；mg为转子重量；Fd，Fq分别为支承转子的可控悬浮力d，q轴分量；km为磁拉力常数，它与无轴承永磁同步电机的本体结构、绕组每相串联匝数、绕组定转子互感、气隙长度、定子内径和铁心长度等参数有关[14]，此处经折算得km=275.2 N/（A2·mm）。

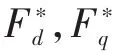
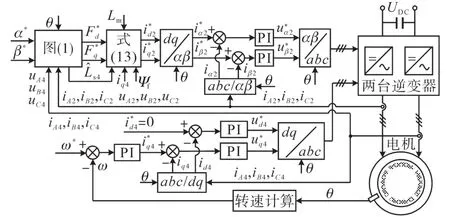
图2 无轴承永磁同步电机位移估算控制框图Fig.2 The block diagram of displacement estimation control for the bearingless PMSM

3 仿真及实验验证

3.1 仿真分析

为了验证上述混合加权最小二乘法位移检测策略的可行性，对1台无轴承永磁同步电机悬浮和转动系统进行了仿真研究。

依据图2构建系统仿真模型，实验样机主要参数如下：额定功率PN=1 kW，额定转速nN=1 500 r/min，转矩绕组极对数pn4=2，转矩绕组自感Ls4=2.6 mH，转矩绕组电阻Rs4=2.3 Ω，悬浮绕组极对数pn2=1，悬浮绕组自感Ls2=1.9 mH，悬浮绕组电阻Rs2=1.9 Ω，转动惯量 Jn=0.000 422 kg·m2，等效励磁磁链Ψf=0.31 Wb，等效励磁电流if=48 A，安全防护轴承间隙δ=0.25 mm。

图3为转矩波动下α轴转子位移响应波形。

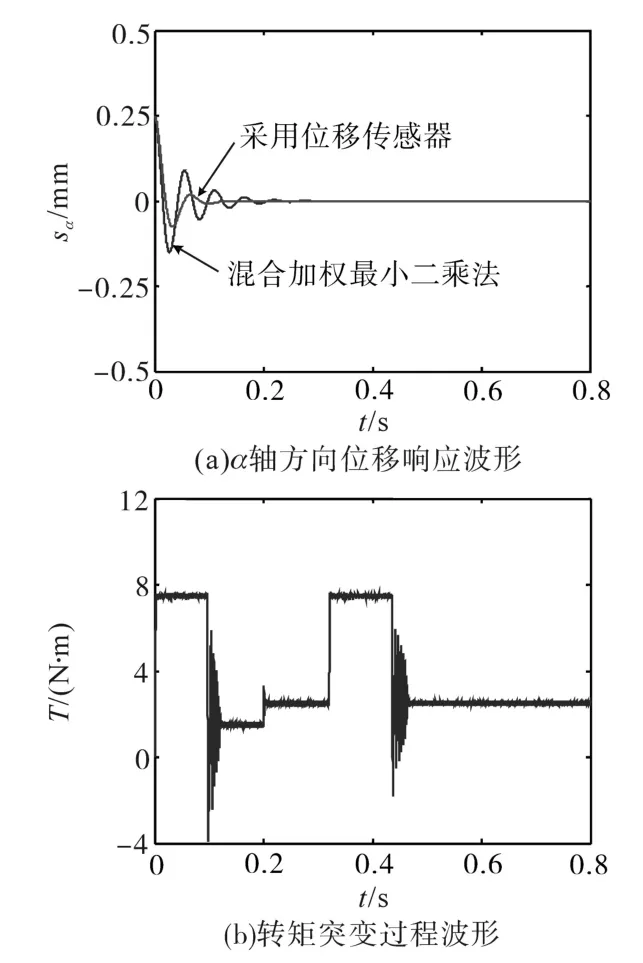
图3 转矩突变下α轴的转子位移响应波形Fig.3 Response waveforms of α-axis rotor displacement under torque sudden changed

图3a同时给出了转子α轴实际位移波形和估算位移响应波形，转子实际位移由位移传感器检测系统获取，转子估算位移经混合加权最小二乘法模型得到。图3a中转子位移的变动过程为：初始偏心位移给定sα=0.25 mm，控制方向为sα=0 mm。由图看出转子在0～0.2 s快速启动阶段，混合加权最小二乘法估算位移比传感器实际检测位移的辨识误差和调节时间稍大，位移估算法能使转子在0.3 s后达到稳定状态，采用估算法的悬浮系统收敛速度较好，此外α轴位移归零后受转矩干扰的影响几乎没有。图3b为转矩突变过程波形，转子带1.5 N·m负载转矩起浮，在0.2 s时给定负载跃变为2.5 N·m，图中转矩系统能跟随参考指令动态调节，转矩控制系统运行正常。转子β轴方向位移控制规律及特性同α轴相似，此处不重复论述。

图4为转速突变情况下β轴转子位移响应特性波形。

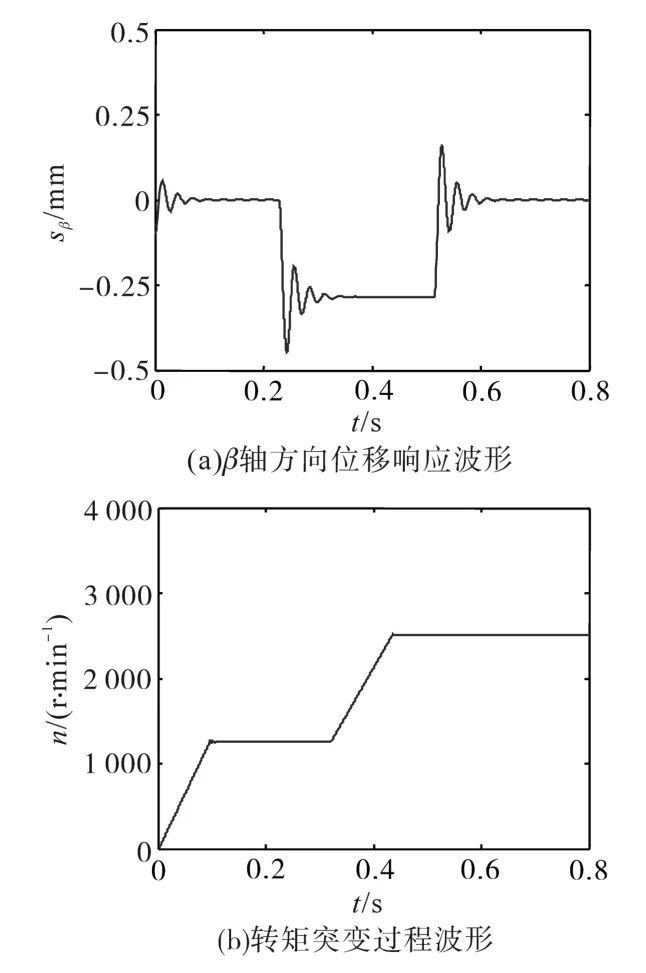
图4 转速突变下β轴转子位移响应波形Fig.4 Response waveforms of β-axis rotor displacement under speed sudden changed

图4a中，转子β轴初始偏心坐标为sβ=-0.1 mm，初始启动目标值为sβ=0 mm，在0.23 s时目标值下降为sβ=-0.3 mm，在0.52 s时目标值返回sβ=0 mm位置。图中β轴转子运动轨迹有多处突变，转子径向位移仅在每一次启动调节阶段有一定的偏移量调整，动态跟随性能较好，并且转子位移波形几乎不受转速调节的影响。此处转子α轴位移调节特性与β轴相似，不再重复论述。图4b转速变化波形中，转速初始给定为1 250 r/min，在0.32 s时转速指令为2 500 r/min，转速突变全过程中，能很好地跟随目标设定值，调速性能较为理想。

图5为混合加权最小二乘法与普通最小二乘法和遗忘因子最小二乘法下转子径向位移对比波形（此时电机转矩和转速按照图3、图4中条件设定），图5中仅给出β轴位移波形（α轴同β轴位移波动规律相同），上述不同方法下转子起浮位置相同，设定为sβ=-0.18 mm，终点悬浮位置为sβ=0 mm。

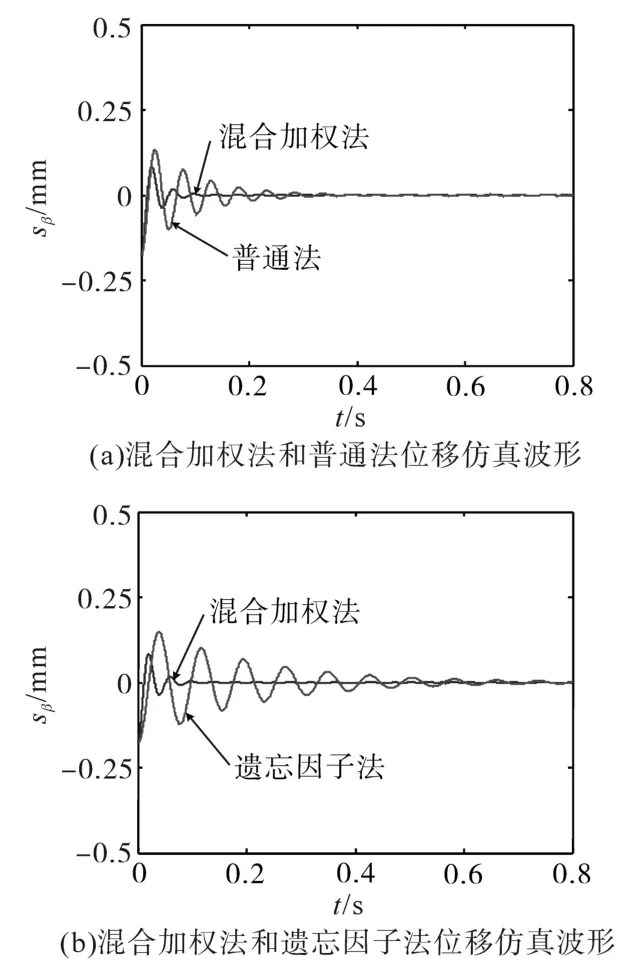
图5 β轴转子位移仿真波形对比Fig.5 Simulation waveforms comparison of β-axis rotor displacement

图5a中混合加权最小二乘法约0.1 s后达到指定位置，而普通最小二乘法至少需要0.3 s，可见加权最小二乘法的收敛速度更快。图5b中遗忘因子最小二乘法转子位移振动幅度和稳态误差较大，到达指定位置振荡时间较长，混合加权最小二乘法具有更快的响应特性和稳态精度。

3.2 实验结果

无轴承永磁同步电机的研制尚无规范的工艺流程和制造方法，样机的研制可在一台普通永磁型同步电机基础上，只需对定子绕组进行工艺上的改装即可。要实现无轴承永磁同步电机转子的整体悬浮，需要对电机转轴两端的径向位置和转轴横向位置（共5个自由度）进行多变量全局控制，控制难度很大。为简化实验，样机设计中转轴一端用球轴承固定，用于轴向和径向承载，在转轴另一端开展悬浮实验，转轴悬浮端必须安装防护轴承，防止转子跌落破坏定子绕组，防护轴承与转子之间的气隙值为0.25 mm，样机简化的特征结构如图6所示。

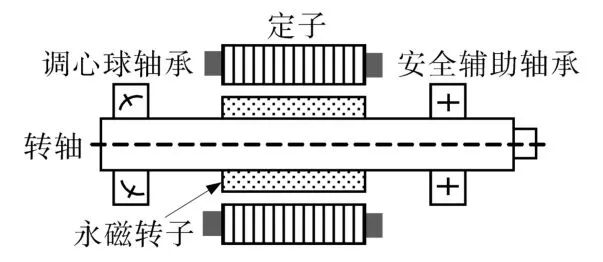
图6 样机特征结构简图Fig.6 Characteristic structure of the prototype motor

样机实验平台和硬件系统组成框图分别如图7和图8所示。

图7 样机实验平台Fig.7 Experimental platform of the prototype motor

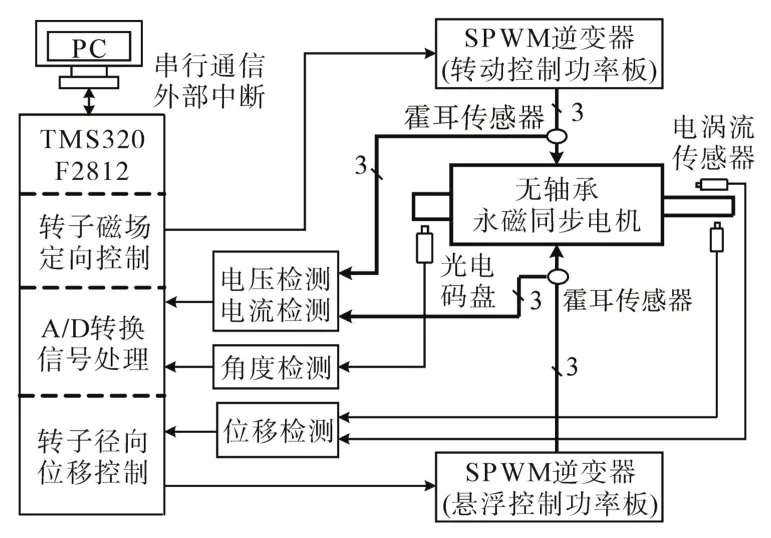
图8 实验硬件系统组成框图Fig.8 Block diagram of experimental hardware system

样机实验平台系统硬件主要包含实验样机、DSP控制芯片（TMS320F2812）、两块SPWM逆变器、电压电流采样电路、位移传感器检测及信号调理电路、光电码盘转子位置采集及接口电路等，光电码盘、电涡流位移传感器（有位移传感器算法采用）和电压电流传感器采集的转子位置、位移和电压电流信号分别送入DSP，电机转动系统和转子位移估算策略的控制算法在DSP中由软件实现。

本实验中，电机空载运行，实验目的是验证文中所提转子位移估算策略的有效性，同时检验样机设计和软、硬件设计的正确性，重点分析电机悬浮运行下的稳态特性。

图9为空载下电机转速调节特性波形，图9a中电机初始启动，转速首次阶跃为1 250 r/min，整个过程较为稳定。图9b为转速从稳定值1 250 r/min阶跃为2 500 r/min的变化过程波形，转速突变过程稳定，调速特性较好。

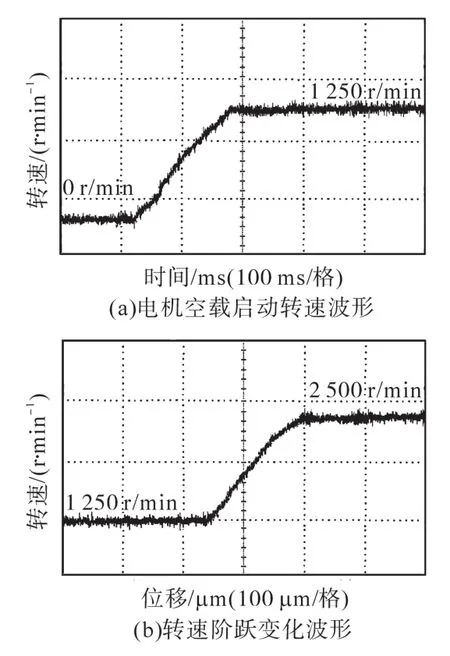
图9 空载下电机转速调节特性波形Fig.9 Motor speed regulation characteristic waveforms with no load

图10为无轴承永磁同步电机在转速1500r/min时转子径向振动轨迹。由图10可以发现，α，β轴方向转子径向位移波动规律基本相同，转子围绕定子中心基本按椭圆形振动，两轴方向转子位移波动最大幅度基本在100 μm左右，未超过安全防护轴承和转子之间的气隙限值，能看出电机转子脱离了安全防护轴承的机械支承，验证了电机转子已处于平稳悬浮状态，实现了较好地悬浮和转动运行。

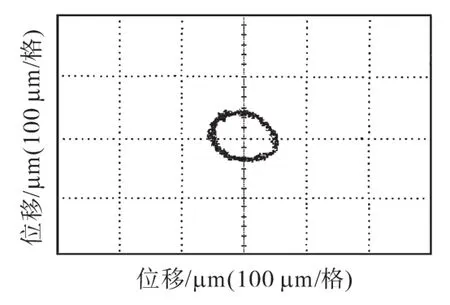
图10 转子径向振动轨迹Fig.10 Radial vibration orbit of the rotor

图11为电机稳态悬浮下（此时电机空载运行，转速为1 500 r/min），分别采用混合加权最小二乘法、普通最小二乘法及遗忘因子最小二乘法的转子位移实验波形。图11a中给出了α轴方向混合加权最小二乘法和普通最小二乘法转子位移比较波形（此时β轴位移变化规律与α轴相同），稳态运行下普通最小二乘法的转子位移偏移量要大，混合加权法的位移收敛性能更好。图11b将β轴方向混合加权最小二乘法和遗忘因子最小二乘法位移波形进行了对比（此时α轴位移变化规律与β轴相同），可以看出混合加权法的转子位移振荡范围更小，混合加权法对转子位移的闭环控制特性更好。

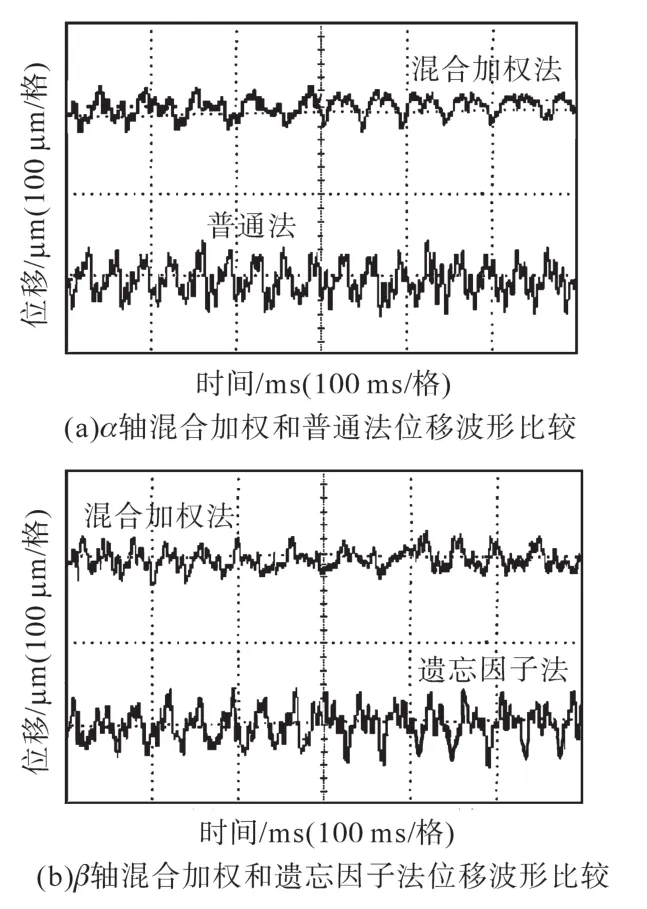
图11 不同方法下转子位移实验波形Fig.11 Rotor displacement experimental waveforms by different methods

4 结论

实现无轴承永磁同步电机悬浮运行实时可控的关键是对转子位移的准确检测，以表贴式无轴承永磁同步电机为研究对象，提出了一种配备低通滤波器的混合加权最小二乘法转子位移估算模型，用以取代价格昂贵的机械位移传感器。该估算方法结合了普通最小二乘法和遗忘因子最小二乘法两种辨识方法优点，电机转子径向位移的观测精度能够满足电机悬浮实际需求，仿真和实验表明了电机转动和悬浮整体控制特性较好。