低输入直流电压的单级双向并网变换器设计

王开林，胡昊 ，陈靖，袁辉，史雪梅，王水英

（1.国网蚌埠供电公司，安徽 蚌埠 233000；2.国网安徽省电力公司检修公司，安徽 蚌埠 233000）

基于电池组的储能系统（energy storage sys⁃tem，ESS）由于对能量管理灵活，目前在诸如新能源接入、电力传动等领域得到了广泛应用[1-3]。ESS需要及时响应能量需求的变化，即有必要在ESS的电池和电网之间设计双向变换器，以保证在峰值负载期间和中断期间平稳运行。通常，双向变换器必须满足几个要求[4-5]，包括双向能量变换能力、高效率、高电能质量、高功率因数（power factor，PF）以及并网后的低总谐波失真（total har⁃monic distortion，THD）。

图1为双向变换器框图。图1a为传统两级双向变换器示意图[6-8]，其中双向DC/DC和DC/AC变换器都进行高频功率变换，前者在低电池电压和高直流链路电压之间执行能量转换，后者需将高直流链路电压接入电网。该设计的主要缺点是两级高频变换电路需配置庞大的直流链路电容器，同时由于两级高开关损耗导致了整体效率较低。此外，每级变换都需独立控制，同时电路复杂度高，成本也较高[9-11]。

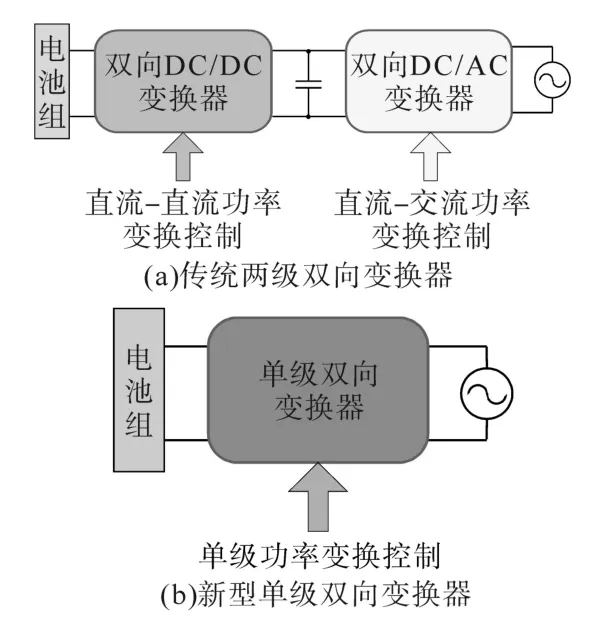
图1 双向变换器框图Fig.1 Block diagram of the bidirectional converter

考虑到双级双向变换器存在诸多缺点，故研究热点往单级双向变换器发展[12-18]，其框图如图1b所示。单级双向变换器在功率变换控制中只需要单控制器，效率高、功率密度高，成本更具竞争力。同时，单级双向变换器不需要庞大的直流链路电容器，且功率器件更少，系统可靠性更高。文献[12-14]设计的单级变换器仅具备降压功能，需要输入直流电压达到或超过电网电压峰值，导致开关应力较高以及大量电池组串、并联以实现输入高压，系统可靠性和功率密度降低。文献[15-18]各自设计了可接入低电池电压的单级双向变换器，但存在大量高频电流纹波，缩短了电池组的寿命[19]，为了抑制高频电流纹波，电池组可能还需要配合使用电解电容器，进一步增加了系统成本。

本文设计了一种新型单级双向并网变换器。新型变换器仅需要单个控制器进行单级功率变换控制，可显著降低功率变换期间的功率损耗。同时，新型变换器电路结构简单，具备升压和降压功能，不需要输入电压覆盖电网电压峰值。同时设计了前馈标称电压补偿器和重复控制算法，实现了较优的功率变换控制效果。最后，进行了实验研究以验证新型变换器的性能。Ss，4个辅助功率开关S1～S4，滤波电容Co和滤波电感Lf，磁电感为Lm的变压器T。Sp和Ss以高频互补的方式工作，S1～S4则以一个较低的频率工作。全桥电路不用于功率变换，即S1和S2在电网电压vg的正半周期期间导通，而S3和S4在vg的负半周期期间导通。全桥电路通过以电网频率fg的低频工作方式将整流后的正弦波展开成电网电压的形式并入电网。Co和Lf构成了低通滤波器以降低并网电流中的谐波含量。

1 新型单级双向变换器的工作原理

图2为新型单级双向变换器的电路图，其包括初级电感Lp，初级电容Cp，2个主功率开关Sp和

图2 新型单级双向变换器电路图Fig.2 Circuit diagram of the novel single-stage bidirectional converter

本文提出的新型单级双向变换器可以基于能量流方向进行工作模式的分类，即可分为放电模式和充电模式。在放电模式下，变换器将电能从电池组侧传输到电网侧，而充电模式中能量流是相反的。

图3为不同工作模式下的等效电路。下面将详述放电模式，因为充电模式是与放电模式完全相反的方式运行的。图4为放电模式下变换器的主要工作波形。图3a中Sp导通，电池组能量传递到Lp，励磁电感Lm接收来自Cp的能量。当Sp断开时，Cp接收在前一时期存储在Lp中的能量。最后，存储在Lp和Lm中的能量被传递到电网。

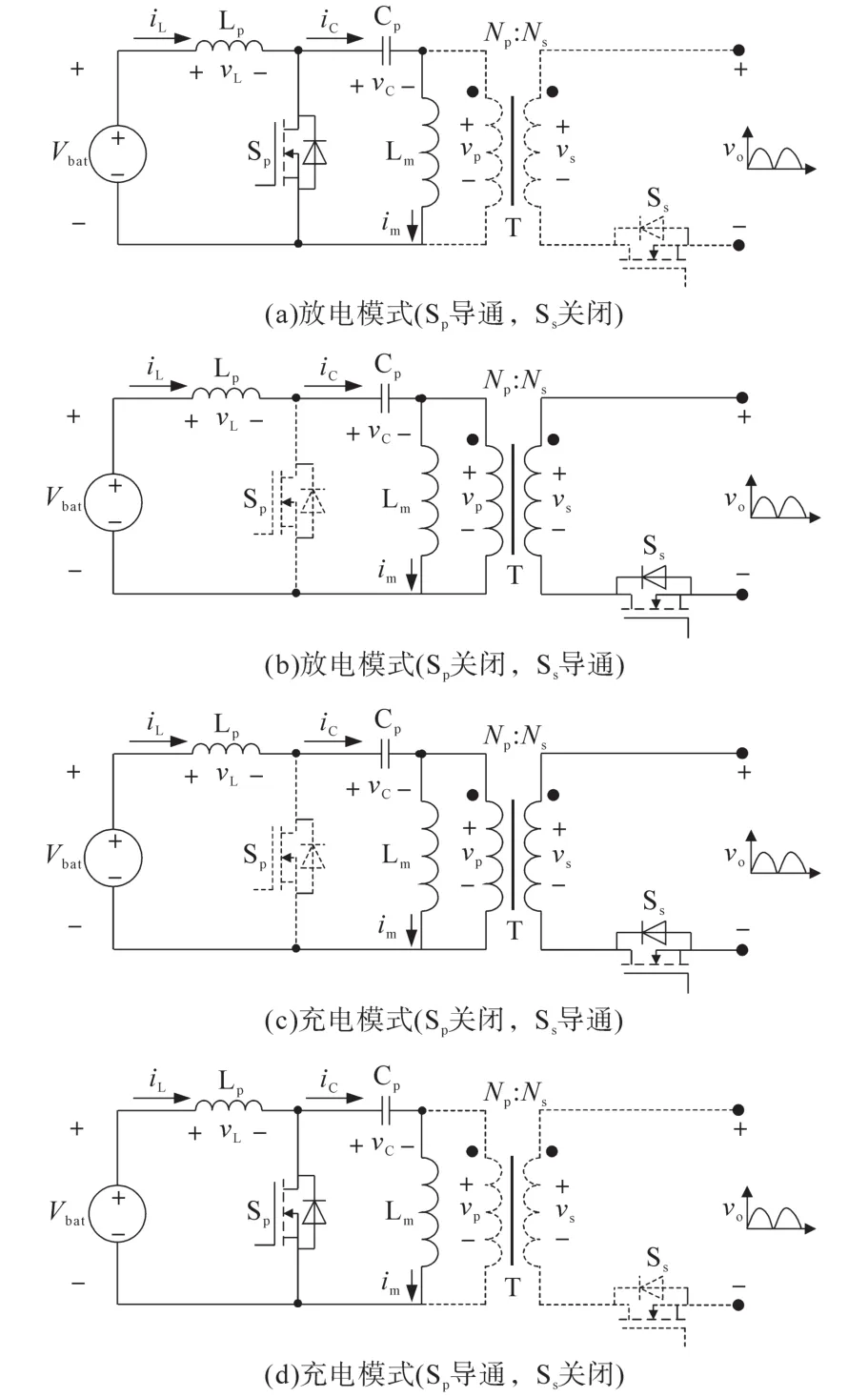
图3 不同工作模式下的等效电路Fig.3 The equivalent circuits under different operating modes

图4 新型单级双向变换器的工作波形Fig.4 The operating waves of the new single-stage bidirectional converter

新型单级双向变换器的工作原理分析基于以下假设：1）功率开关 Sp，Ss以及 S1～S4是理想开关；2）变换器以单位功率因数运行；3）主功率开关Sp，Ss以远高于电网频率的工作频率运行，Co上的电压vo在一个开关周期Ts内可以看做为恒定值；4）初级电容Cp的容值足够大可忽略其相对幅值较小的纹波电压，初级电容上的电压vC可以看做为恒定值。

在Sp的导通和关断期间，电感电压vL为

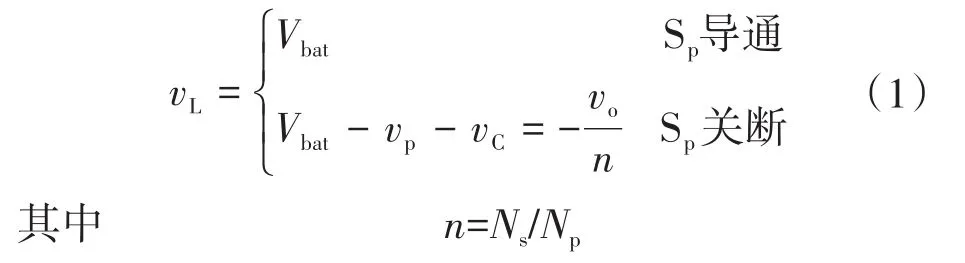
式中：n为匝数比。

根据伏秒平衡原理，初级电感器Lp的平均电压为零，因此放电模式下的电压变换比可计算如下：

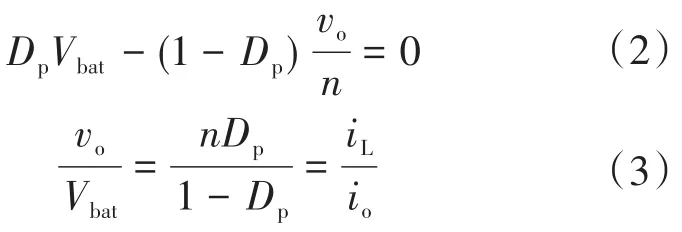
式中：Dp为稳态占空比，即主功率开关Sp的占空比。

在图3c、图3d的充电模式中，次级主功率开关Ss的导通/断开状态下的电感电压vL如下所示：

从式（4）可以看出，充电模式下电压变换比可用伏秒平衡原理来计算。将Sp的占空比定义为稳态占空比Dp时，Ss的占空比为1-Dp，故充电模式下的电压变换比和式（3）一致。将式（3）重写为稳态占空比的表达式如下：

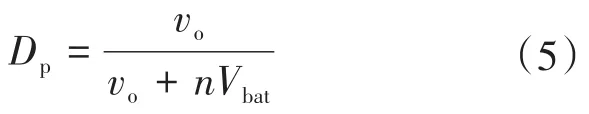
从式（3）可计算出电感电流iL如下所示：

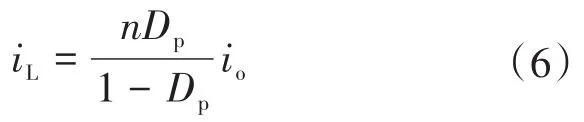
全桥电路输入电流io可用磁化电流im表示为

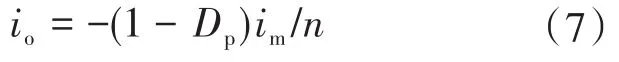
2 控制器设计

新型单级双向变换器只有单级功率控制，但需满足双向能量流控制，以及并网相关要求。全桥电路输入电流io表征了功率流方向、功率大小以及并网电能质量。因此需对io进行控制。

变换器中Sp和Ss以比fg高得多的频率在工作。故一个开关周期Ts内可认为vg是恒定的，并假设vo与vg的绝对值相同。如图3所示，变换器的两个工作状态为：一是Sp导通和Ss断开状态；二是Sp断开和Ss导通状态。假设主功率开关Sp的占空比定义为主占空比D，则根据图3，可推导开关周期平均方程如下：

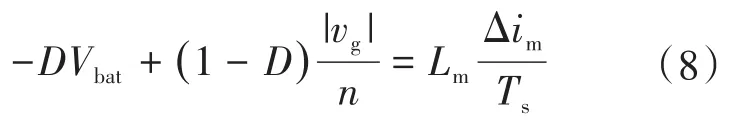
式中：Δim为磁化电流的变化量。

由式（8）可推导出主占空比D的表达式如下：

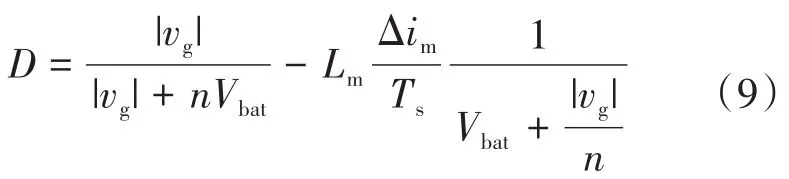
此外，主占空比D可表示为两个占空比之和：

式中：ΔD为控制输出占空比。

联立式（5）、式（9）和式（10），得到ΔD为

为了控制io，可使用Δio表示ΔD，而不是使用式（7）中的Δim，具体如下所示：

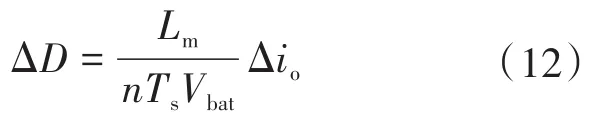
重复控制器为特定频率范围内的周期性参考信号提供精确跟踪。图5为重复控制器的工作原理图。

图5a为重复控制器框图，图5b为重复控制器工作示例。重复控制器基于存储数据重复进行相同的任务以改善控制性能，最终可实现零稳态误差跟踪。此外，重复控制器使用相位超前补偿算法来补偿系统延迟中的相移。

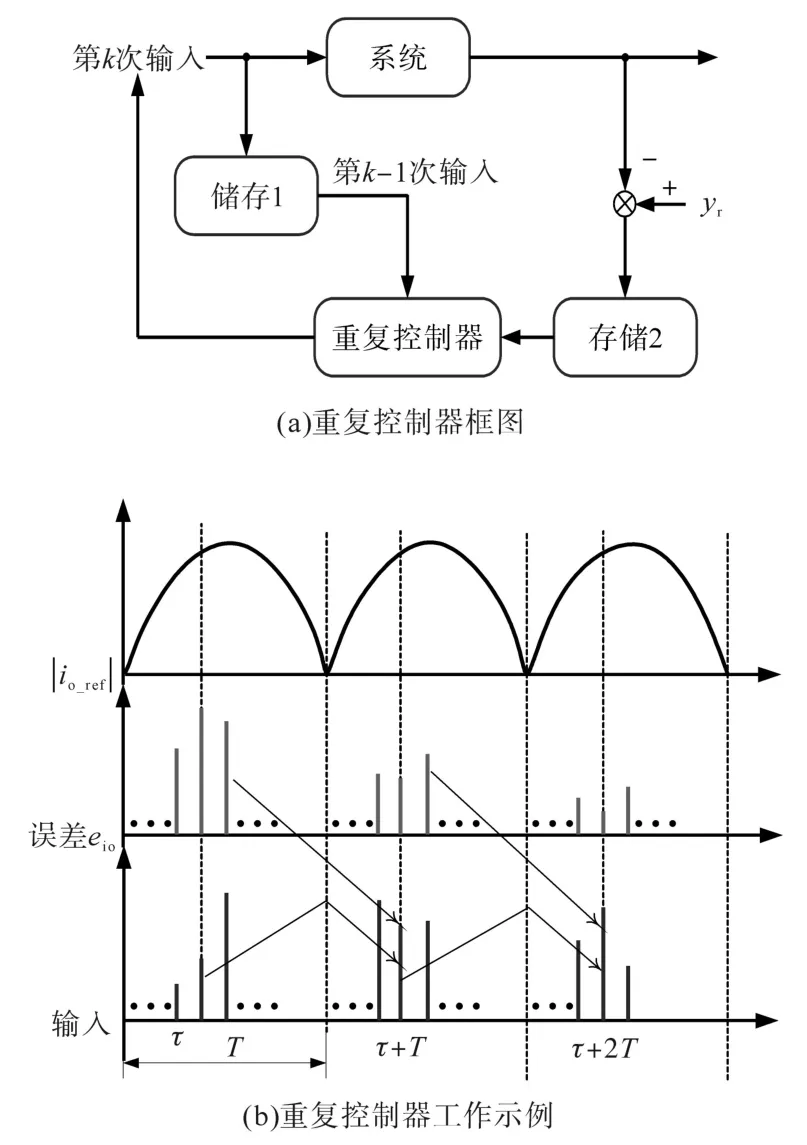
图5 重复控制器的工作原理Fig.5 The operating principle of the repetitive controller

所开发的重复控制器Grc（z）如下所示：

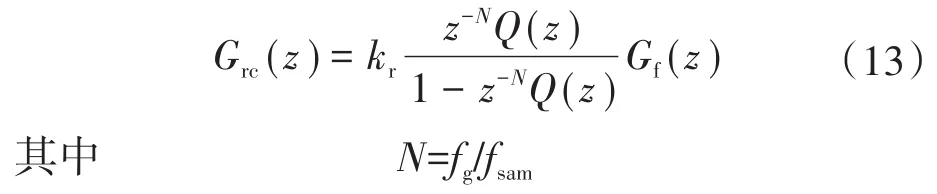
式中：kr为重复控制器增益；fg为电网频率；fsam为采样频率；Gf（z）为数字延迟环节传递函数。

由于系统不确定性，系统延迟和未知扰动很难精确地对Gf（z）进行建模，故本文将Gf（z）表示如下：

式中：m为预测指数。

此外，增加低通滤波器Q（z）以跟踪或拒绝特定频率范围内的周期信号，并保护高频区域的控制。Q（z）通常设置为具有零相移的滑动平均滤波器，如下所示：

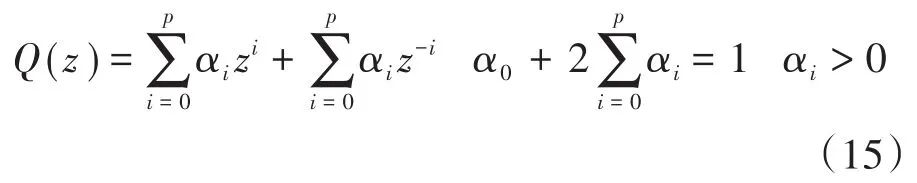
式中：α0～αi为滤波系数；p为滤波采样数，滤波器设置为一阶滤波器。

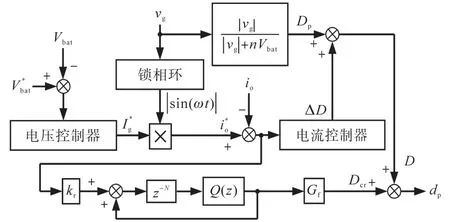
图6 新型单级双向变换器的控制框图Fig.6 Control block diagram of the new single-stage bidirectional converter

在图6所示控制器作用下，新型单级双向变换器可执行工作模式无缝切换和精确的参考电流跟踪控制，并同时抑制由低次谐波引起的干扰。

3 主电路设计

为了推导出电感电流iL（t）和全桥电路输入电流io（t）的平均值，可忽略变换器损耗并基于单位功率因数进行瞬时功率p（t）的计算，即p（t）为

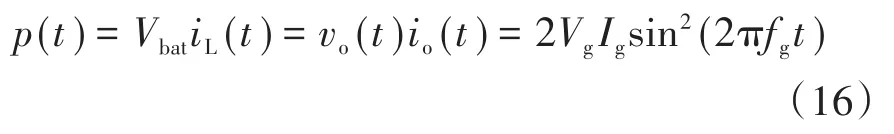
式中：Vg，Ig分别为对应于vo（t），io（t）的有效值；Vbat为标称电池电压；fg为电网频率。

iL（t）和io（t）的平均值可用于导出主功率开关Sp和Ss的峰值电流Ispp和Issp。在所提出的变换器中，设计初级电感Lp、变压器T的磁化电感Lm和匝数比n时需考虑减小主功率开关上的峰值电流和电压，进而降低开关损耗。

此外，由于单级双向并网变换器电路拓扑中变压器的励磁电感电流方向始终是固定的，故在同等功率下，变压器磁芯相对全桥型双级电路需要更大的体积，但考虑到其电路较为简单，所用元件较少，故综合比较，体积还是稍优于全桥型两级变换电路。

表1为主功率开关Sp和Ss的峰值电流和电压应力分析表。如表1所示，峰值电流与n，Lp和Lm相关，峰值电压与n相关。

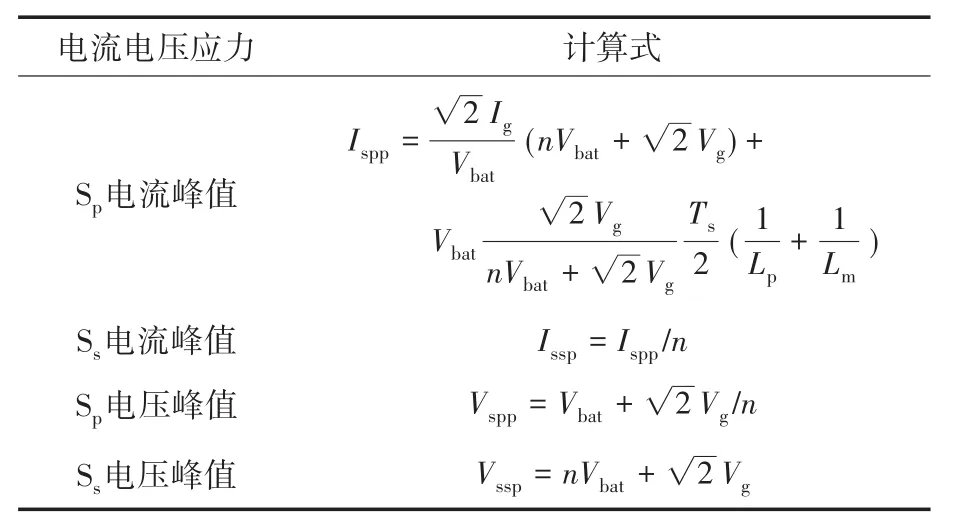
表1 主功率开关电流和电压应力分析Tab.1 Current and voltage stresses analysis of the main power switches

图7为以匝数比n和总电感L=LpLm/（Lp+Lm）为变量的主功率开关Sp和Ss的开关损耗之和变化趋势图。由图7所示，当匝数比n小于4并逐渐减小时，开关损耗迅速增加；同时当匝数比n大于6并逐渐增大时，开关损耗也呈增加趋势，故匝数比n的合理区间是4～6。而总电感L在超过50 μH后不会对开关损耗有较大影响，考虑到L较大将导致变压器和初级电感器较大的体积重量，故Lp和Lm的设计必须综合考虑开关损耗和体积重量，选择L接近50 μH较为合理。此外，Lp在选取时还要满足将最大纹波电流限制在电池电流峰峰值的20%以下。初级电容器Cp的容值需设计得足够大，使纹波电压限制在电池电压10%以下。

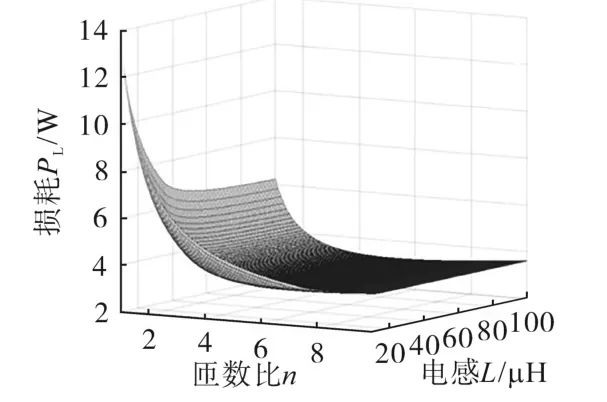
图7 开关损耗随L和n变化图Fig.7 Diagram of the switching losses with L and n changes

由于所设计的单级双向并网变换器电路省去了高压直流母线环节，故存在Sp电流应力较大和Ss电压应力较大。但文献[12-13]中所设计的单级变换器由于要求其输入直流电压达到或超过电网电压峰值，故使用了大量电池组串联以实现输入高压，这导致了直流侧开关管的电压应力高于本文中Ss的电压应力，同时尽管电流应力较小，但所用开关管数量大于本文中的两个，故功率密度明显低于本文中设计的方案。同时，文献[15]和文献[16]中所设计的可接入低电压的单级双向变换器直流侧所用开关管电压应力小于本文中方案，但由于存在大量高频电流纹波，实际上电流应力会大于本文中的方案。

4 实验验证

为了验证所设计的可接入低直流电压的单级双向并网变换器的有效性，开发了功率为250 W的变换器样机并开展了相关实验，其中主功率开关采用MOSFET材质，控制器基于数字芯片dsPIC33EP512GM604实现。实验系统其他参数为：电网电压有效值Vg=220 V，额定频率fg=50 Hz，电池组额定电压Vbat=48 V，变压器初级匝数Np=14，变压器次级匝数Ns=63，励磁电感Lm=56 μH，开关频率fs=50 kHz，初级电容Cp=17.6 μF，初级电感Lp=380 μH，滤波电感Lf=400 μH，初级电容Co=800 nF。

图8为放电模式下主功率开关Sp，Ss的电压、电流实验波形。图9为满载工况下的电网电压vg、并网电流ig实验波形。图9a中vg和ig是同相的，ig的THD=3.69%；图9b中vg和ig是反相的，ig的THD=4.12%。图9中的并网电流过零点有畸变，对电流控制有一定的影响，这是因为所设计电路拓扑中的全桥电路不进行高频功率变换，而只是进行电流改向使用，故这是提高变换效率难以避免的，但并网电能质量总体是符合电网相关标准要求的。

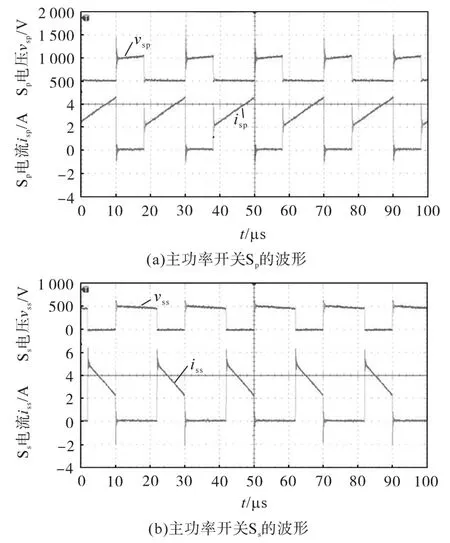
图8 放电模式下主功率开关的电压和电流波形Fig.8 Voltage and current waves of the main power switch in discharge mode

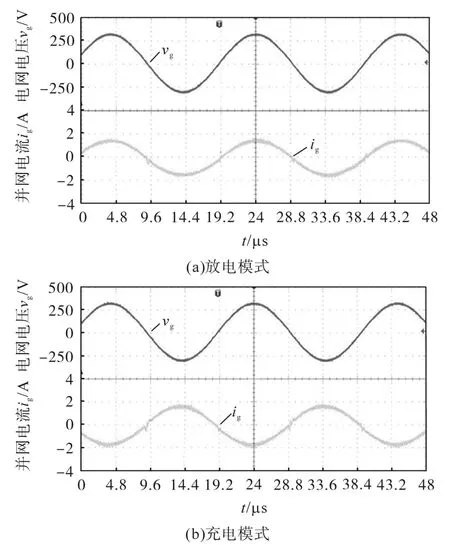
图9 满载工况下的电网电压和并网电流波形Fig.9 Grid voltage and grid-connected current waves under full load condition

图10为放电模式和充电模式下电网电压和电池电流实验波形。由图10可知，电池组电流存在两倍频的电流纹波，根据文献[1-3]的研究，此低频纹波电流会影响电池组寿命，故进一步的研究方向是考虑对此低频电流纹波进行抑制。

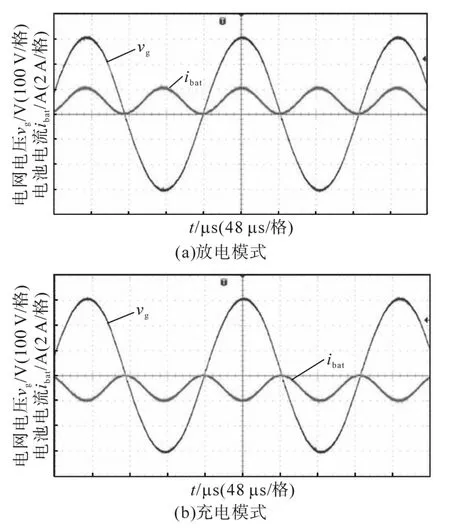
图10 电网电压和电池电流实验波形Fig.10 Experimental waves of the grid voltage and battery current

图11为在放电模式下出现输入电压、电网电压扰动时的实验结果。

图11 放电模式下电压扰动时的实验结果Fig.11 Experimental results of voltage perturbations in discharge mode

图11a中输入电压从40 V上升至56 V，而图11b中电网电压有效值从200 V增加至240 V，两种情况下，所设计的控制器均能快速响应，稳定住并网电流。图12为变换器从放电模式切换至充电模式时的实验波形，从电网电压vg和并网电流ig的波形可看出，所设计的变换器不同模式之间是可以无缝切换的。

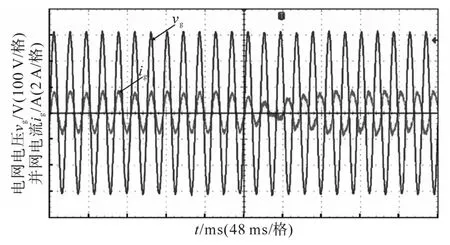
图12 变换器模式切换实验结果Fig.12 Experiment results of the converter with mode switching

图13为不同工况下测得的功率转换效率结果，效率由数字功率计（Yokogawa WT130）测量。

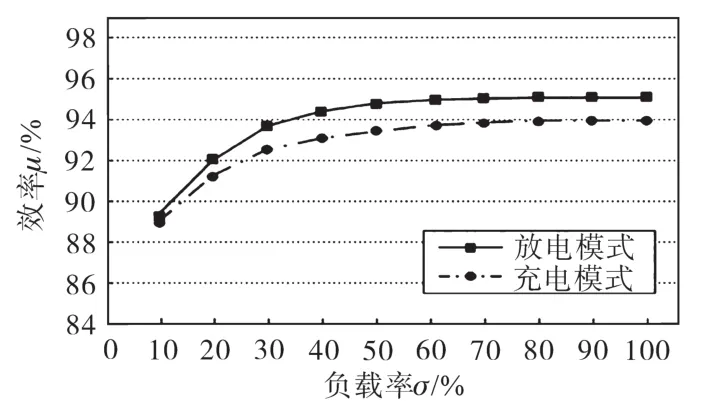
图13 变换器效率测试结果Fig.13 Efficiency test results of the converter

表2为不同方案下变换器效率对比结果。与传统双级变换器[20-21]的效率对比，数据显示由于传统双级变换器具有两级功率变换，并具有更多的功率开关器件，故难以实现整体提高效率。

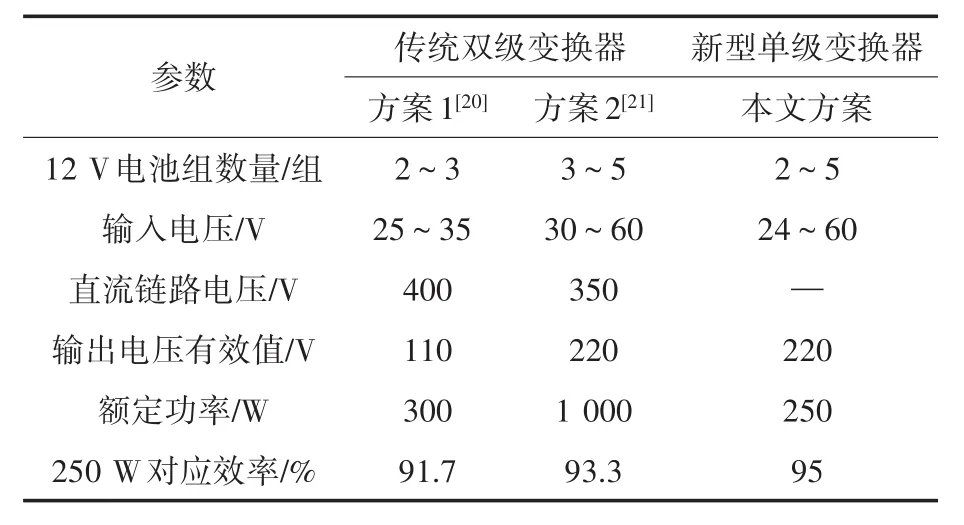
表2 效率对比结果Tab.2 Efficiency comparison results

5 结论

为了实现储能系统高效并网，提出了一种可接入低直流电压的高效率单级双向并网变换器，同时开展了变换器的主电路和控制器设计，完成了相关实验，现总结主要结论如下：

1）所设计的双向并网变换器包含直流变换电路和全桥电路，但只有前者进行高频功率变换实现升压和降压，整个变换器系统电路结构简单，可覆盖峰值电网电压，无需较高的直流电压，提高了电池组寿命和功率密度。

2）控制器基于前馈标称电压补偿器和重复控制算法实现，前者减轻了电网电流控制负担，后者确保了精确的电流参考值跟踪控制。

3）实验结果表明，新型单级双向并网变换器相对于传统双级变换器具有更高的效率，且控制性能优良。

4）需要进一步研究的内容为对变换器中存在的低频电流纹波进行抑制，以及进行更高功率等级的实验验证。