单极性电流控制半桥电压平衡电路研究

张先进，吴迪

（1.江苏工程职业技术学院江苏省风光互补发电工程技术研发中心，江苏 南通 226007；2.江苏海洋大学电子工程学院，江苏 连云港 222005）

微型直流电网是一种非常有效的直流输电系统，它能够将新能源和储能单元等有机组网，向用户提供高质量的电能[1-9]。微型直流电网常采用两线制输电方式，电网中只有一个母线电压。因此，为了满足用户端不同用电设备对输入电压的需求，通常要在用户端构造一根中线将此母线电压转变成两个等级相同或不同的直流电压[5-9]。

能够实现该功能的变换器常有半桥电压平衡电路[5-8]和双降压半桥电压平衡电路[9]等。半桥电压平衡电路除了应用在微型直流电网[5-7]或单相整流供电系统[8]之中，还可以平衡串联电容或电池组电压[10]。半桥电压平衡电路如图1所示。

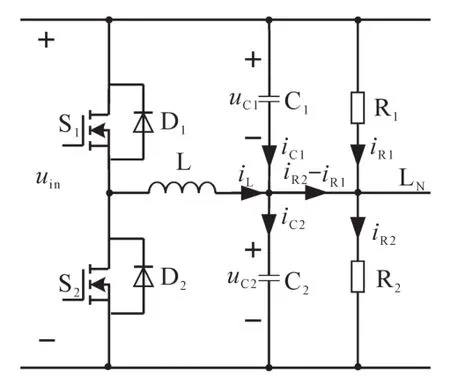
图1 半桥电压平衡电路Fig.1 The balancing circuit with half-bridge voltage

图1中电感电流iL平均值等于两个不平衡负载（R1，R2）电流之差。为了简化控制，半桥电压平衡电路常采用互补驱动[6-8，10]。图2为互补驱动双极性电感电流 iL和 S1，S2驱动 Ugs1，Ugs2波形。由图2可知不平衡负载电流差值小时，电感电流运行在双极性条件下，半桥电压平衡电路输入和输出端之间存在无功电流交换。

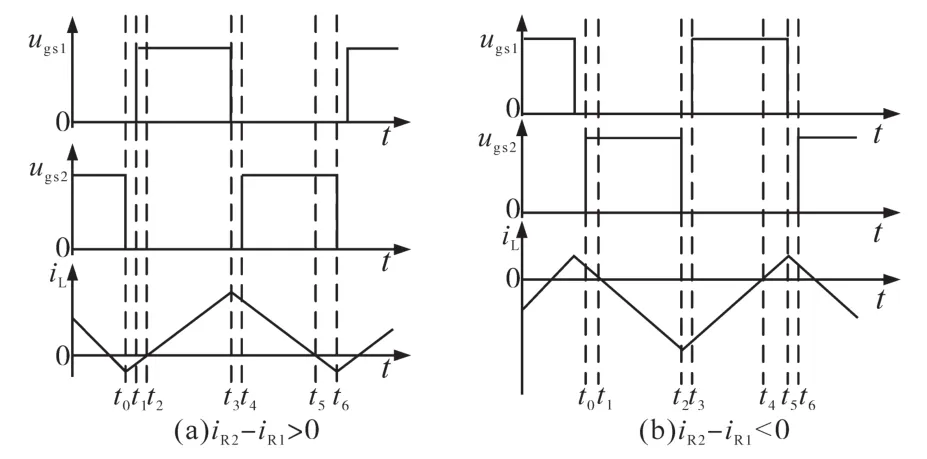
图2 互补驱动时双极性电感电流和驱动波形Fig.2 Bipolar inductor current and driving signals under complementary driving method

文献[9]从半桥电压平衡电路存在的潜在直通和无功电流等角度出发，研究了双降压半桥电压平衡电路，并通过适当的控制使每只电感中电流分别单极性运行。但是，与半桥电压平衡电路相比，该电路结构复杂、所需器件较多、成本较高。

为了充分利用半桥电压平衡电路结构特点，并消除无功电流，本文研究了一种半桥电压平衡电路的单极性电流控制方法，并详细分析在此方法下的工作原理。最后，进行了仿真和实验验证。

1 半桥电压平衡电路和单极性控制方法

1.1 电路结构

半桥电压平衡电路如图1[5-8]所示，它由半桥拓扑、串联输出电容C1和C2等组成，结构十分简单。图1中，R1，R2为两个不平衡负载所对应的等效电阻；LN为中线。因此，在办公等场合与大地相连的中线能够大大地提高可靠性[5-9]。在实际应用中，根据需要图1中uC1可以等于uC2也可以不等于uC2[5]。在互补驱动时，当不平衡负载电流之差较小时电感电流双极性运行，波形如图2所示。

1.2 单极性电流控制方法

电流单极性控制等数电路如图3所示。以uC1=uC2为控制目标的电感电流iL单极性工作基本思路：电感电流iL平均值IL大于零时，S1工作、S2不工作（见图3a）；电感电流平均值IL小于零时，S2工作、S1不工作（见图3b所示）。这样，图1就可以工作在类似于两个Buck电路情况下，避免了电感电流在开关周期内可能出现图3双极性情况。其控制原理框图如图4所示。

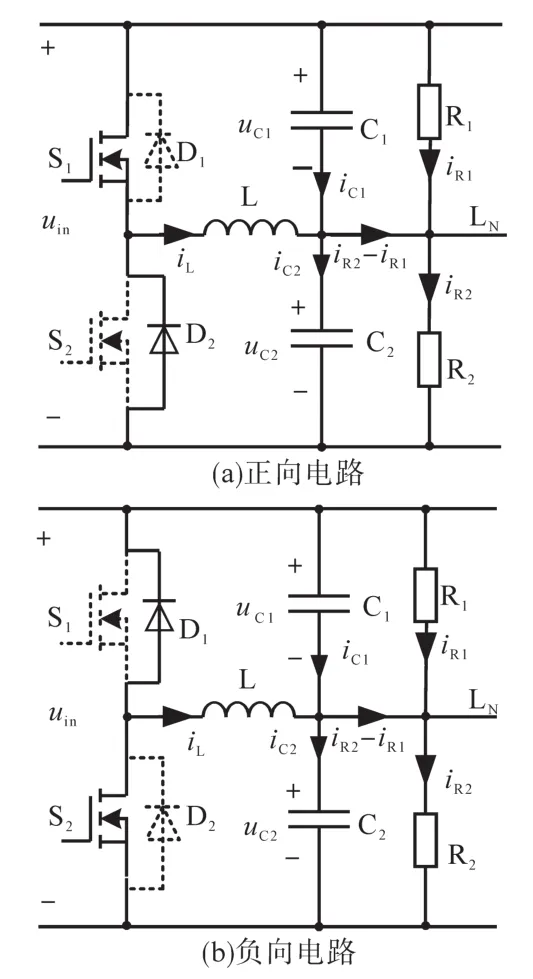
图3 电流单极性控制等效电路Fig.3 Equivalent circuit under a unipolar current control method

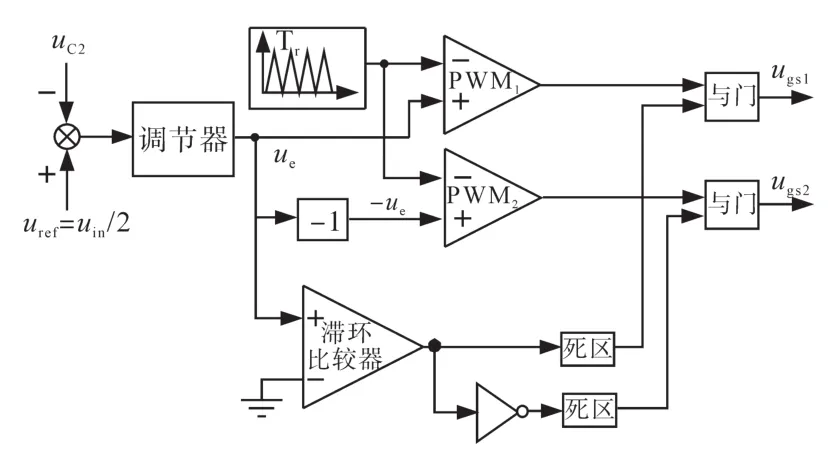
图4 单极性电流控制原理框图Fig.4 Diagram of the proposed unipolar current control

图4中输入电压uin一半作为输出电压uC2图4参考值，ugs1和ugs2分别是开关管S1和S2的驱动信号。为了避免S1和S2频繁地切换，采用滞环比较器，死区是为了避免S1和S2切换时出现的直通危险。

结合图3和图4，稳态时基本原理描述如下：

1）当不平衡负载R1＞ R2（负载电流iR1＜ iR2）时，负载处在不平衡状态，电压调节器输出为正值，S1工作、S2不工作；输入电压uin通过电感L向负载R2提供不平衡负载电流差值（iR2-iR1），即电感电流iL的平均值IL大于零。

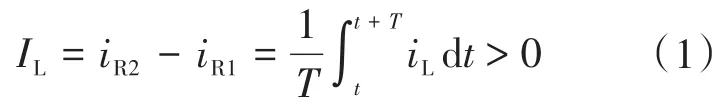
式中：T为开关周期。

2）当不平衡负载R1＜ R2（负载电流iR1＞ iR2）时，负载处在不平衡状态，电压调节器输出为负值，S2工作、S1不工作；输入电压uin通过电感L向负载R1提供不平衡负载电流差值（iR2-iR1），电感电流iL的平均值IL小于零。

3）当不平衡负载R1=R2时，负载处在平衡状态，电感电流iL的平均值IL近似为零。这与Buck变换器工作在空载时情况类似。

根据前文所述，电感电流平均值IL大于零时，电流单极性控制的波形如图5所示（电感电流平均值IL小于零的波形图在此忽略）。根据单极性电感电流iL情况，电感电流平均值IL大于零又分为：电感电流iL连续模式（CCM，不平衡负载电流差值大，图5a所示）和断续模式（DCM，不平衡负载电流差值小，图5b所示）。

图5 电感电流平均值IL大于零时单极性电感电流和驱动波形图Fig.5 Unipolar inductor current and driving signals under the inductor current average value IL＞0

对比图2和图5b，可以看出：

1）不平衡负载电流差值小时，单极性电流控制下电感电流是单极性的，输入和输出端之间不存在无功电流；

2）互补驱动时电感电流是双极性的，输入和输出端之间存在无功电流。

2 工作原理分析

根据前面的基本原理描述，依据电感电流平均值的情况，电路工作过程具体分为IL大于零、IL小于零和IL等于零三种状态。下面仅对IL大于零状态进行分析，其他情况不再赘述。

为了简化分析，假设所有器件均为理想器件，电容C1，C2相等且为无穷大；电路工作在稳态，即电容电压uC1=uC2。

下面仅分别对电感电流平均值IL大于零时，CCM和DCM下半桥电压平衡电路的工作原理进行分析。

2.1 电感电流iL连续模式

电感电流iL在连续模式下的主要驱动信号和电感电流波形如图5a所示，其等效电路如图6所示。

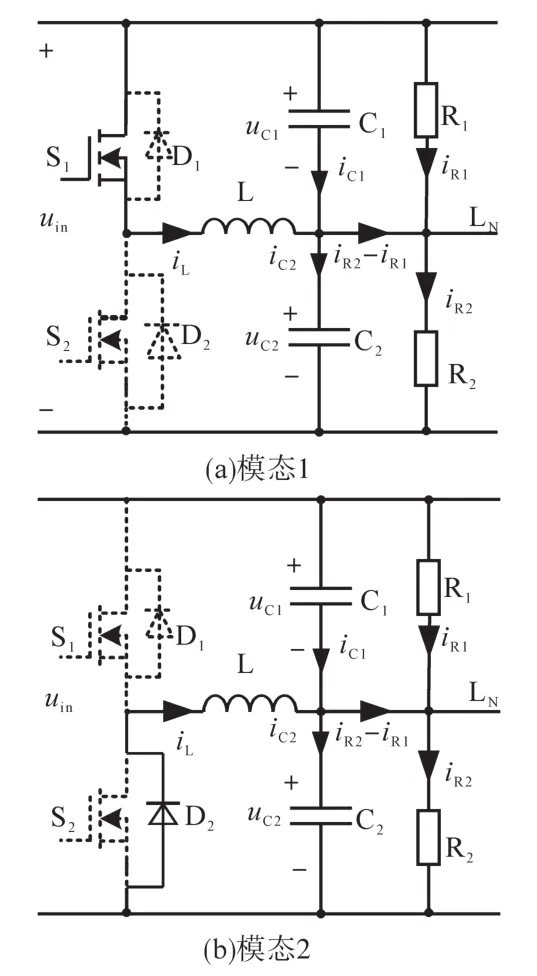
图6 电感电流连续时等效电路Fig.6 Equivalent circuits under CCM

1）模态1[t1—t2]：此时，S1导通、S2关断（见图5a和图6a）。在t1时刻之前S1关断，电流iL通过S2的体二极管D2续流。在t1时刻开通S1，电流iL将从D2切换到S1。在电感L上电压uL=uin-uC2=uC1的作用下，电感电流iL开始线性上升。该过程持续到t2时刻关断S1为止。

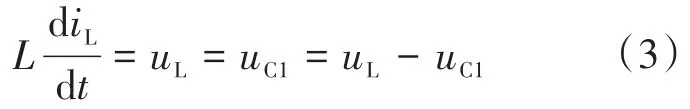
2）模态2[t2—t3]：此时，S1，S2关断，D2导通（见图5a和图6b）。在t2时刻关断S1，电流iL将再次从S1切换到D2续流。在这一模态中，电感上电压uL=-uC2，电感电流iL从最大值开始线性下降，直到t3时刻再次开通S1为止。

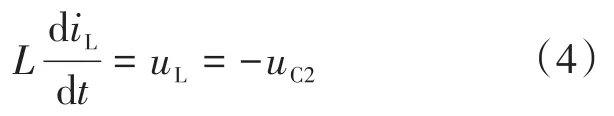
从t3时刻起，进入下一个工作周期。

由于稳态时uC1=uC2，所以根据伏秒积平衡原理，由式（3）和式（4）可以得到下式：

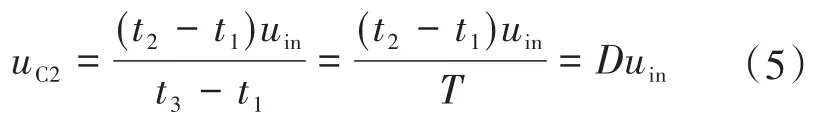
式中：D为S1的占空比。

显然，这与Buck变换器工作在CCM模式时输入输出关系一致。

2.2 电感电流iL断续模式

电感电流iL断续模式状态下主要驱动信号和电感电流波形如图5b所示，其等效电路如图6和图7所示。

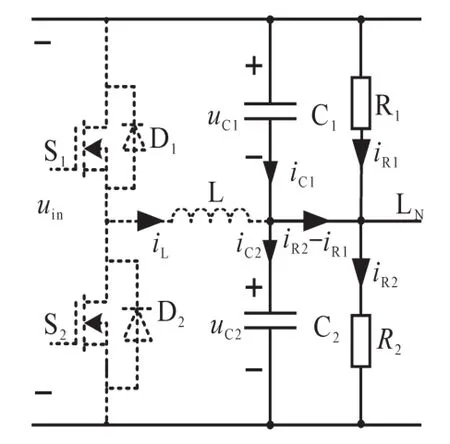
图7 电感电流断续时模态3等效电路Fig.7 Equivalent circuits of mode 3 under DCM

1）模态1[t1—t2]：此时，S1导通、S2关断（见图5b和图6a）。在t1时刻之前由于电流iL为零，所以在t1时刻开通S1是零电流开通。在电感L电压uL=uin-uC2=uC1作用下，电流iL从零开始线性上升。该过程一直持续到t2时刻关断S1为止。

2）模态2[t2—t3]：此时，S1，S2关断，D2导通（见图5b和图6b）。在t2时刻关断S1，电流iL将从S1切换到D2续流。在电感L电压uL=-uC2作用下，电流iL开始线性下降，直到t3时刻电流iL下降至零为止。

3）模态 3[t3—t4]：此时，S1，S2关断（见图5b和图7）。从t3时刻起，所有功率器件都没有电流流过。直到t4时刻再次开通S1，进入下一个开关周期。

由于稳态时uC1=uC2，所以根据伏秒积平衡原理，可以得到下式：

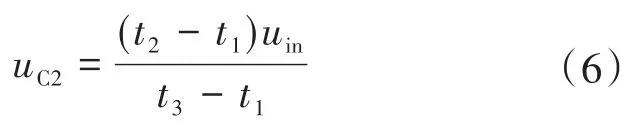
显然，这与Buck变换器工作在DCM模式时输入输出关系一致。

3 仿真与实验

3.1 仿真分析

仿真条件：开关频率约25 kHz，L=230 μH，C1=C2=470 μF，死区近似为 2 μs，输入电压360 V。

图8为电感电流平均值IL大于零时仿真图，图9为电感电流平均值IL小于零时仿真图。其中，图8a、图8b中负载电流分别为iR1=2.8 A，iR2=6.2 A和iR1=1 A，iR2=13.4 A；图9a和图9b中负载电流分别为iR1=5.0 A，iR2=2.4 A和iR1=12.8 A，iR2=2.2A。

由图8、图9可见，在不同负载条件下，仿真结果与前面的分析是一致的。

图8 电感电流平均值IL大于零仿真结果Fig.8 Simulation results under IL＞0

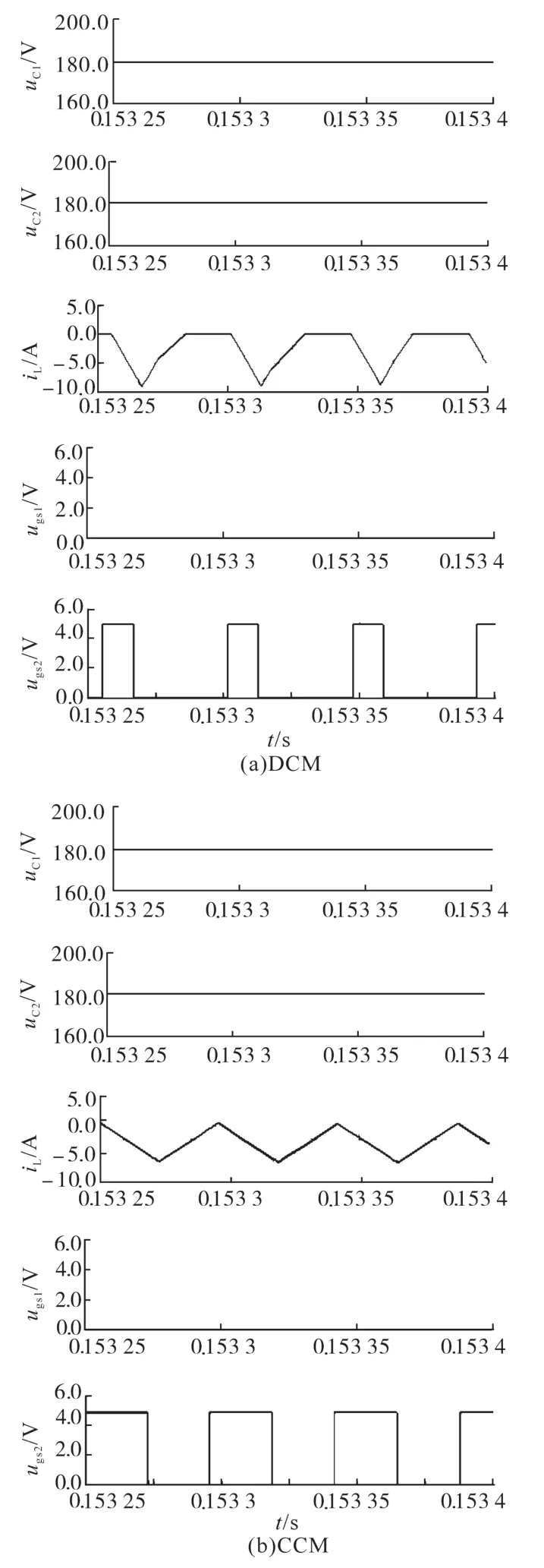
图9 电感电流平均值IL小于零仿真结果Fig.9 Simulation results under IL＜0

3.2 实验分析

为了验证前面的分析，进行实验验证，主要参数与仿真参数一致。其中，S1和S2分别采用SPW47N60C3半导体，电感采用EE55铁氧体，C1和C2为470 μF的电解电容。

图10为电感电流平均值IL大于零时主要实验波形图。其中，图10a为uC1=180.3V，uC2=180.1V，iR1=2.8 A和iR2=6.2 A时，电感电流iL断续实验波形；图10b为uC1=180.3 V、uC2=180.0 V，iR1=1.0 A和iR2=13.4 A时，电感电流iL连续实验波形。图11为电感电流平均值IL小于零时实验波形图。其中，图11a为uC1=180.1 V，uC2=179.9 V，iR1=5.0 A，iR2=2.4 A时，电感电流iL断续实验波形；图11b为uC1=179.8 V，uC2=180.0 V，iR1=12.8 A，iR2=2.2 A时，电感电流iL连续实验波形。

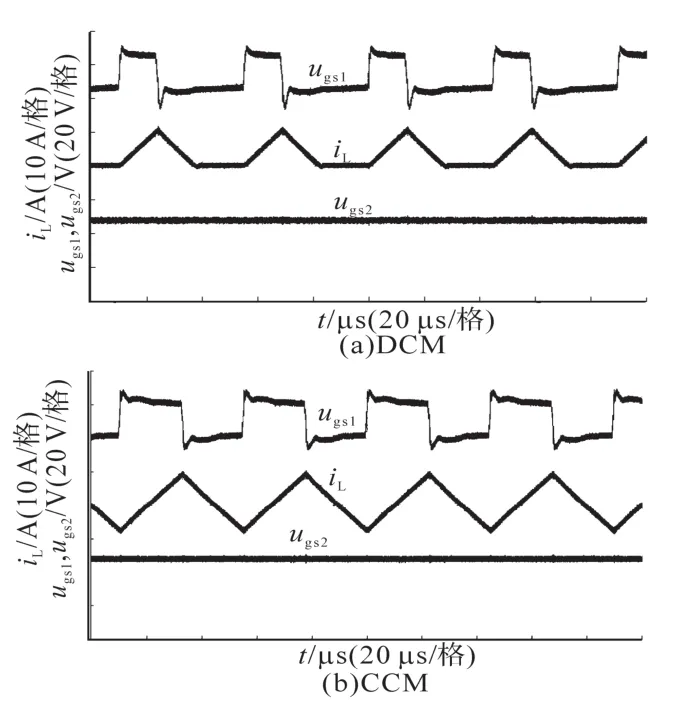
图10 电感电流平均值大于零实验波形Fig.10 Experiment results under ILabove zero

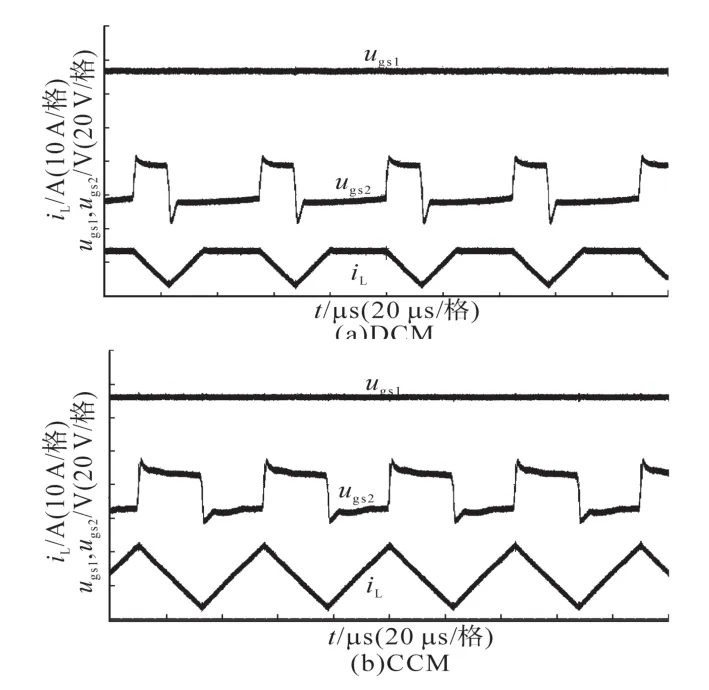
图11 电感电流平均值小于零实验波形Fig.11 Experiment results under ILbelow zero

由图10、图11可见，不论不平衡负载电流|iR2-iR1|偏差如何，电感电流都是单极性的。因此，输入和输出端不存在无功电流交换问题。

图12和图13分别为负载R1和R2电流突变时实验波形。图12中负载电阻R2电流iR2=1.20 A不变，负载电阻R1电流iR1在1.0～7.5 A之间变化时实验波形。同时测出iR1=1.0 A时输出电压uC1=179.7 V，uC2=179.9 V，iR1=7.5 A时输出电压uC1=179.5 V，uC2=179.6 V。图13为负载R1电流iR1=1.2 A不变，负载电阻R2电流iR2在0.0～5.0 A之间变化时实验波形。同时测出iR2=0.0 A时输出电压uC1=179.7 V，uC2=180.1 V，iR2=5.0 A时输出电压uC1=179.4 V，uC2=179.7 V。

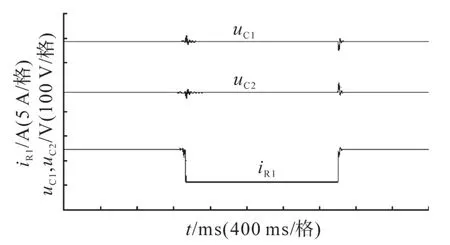
图12 负载R1电流iR1突变实验波形图Fig.12 Experimental waveforms under transiently changing iR1

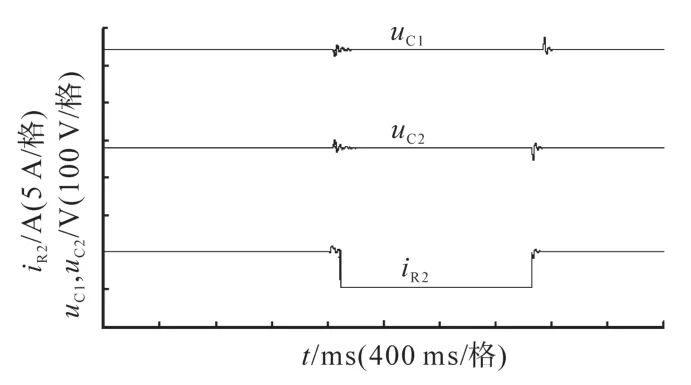
图13 负载R2电流iR2突变实验波形图Fig.13 Experimental waveforms under transiently changing iR2

由图12，图13可以看出在负载突变时，输出电压仍然能够很好地平衡输入电压，但是输出电压有明显的尖峰。这可以通过优化参数来减少尖峰。

下面给出不同负载和输入电压下实验数据。电感电流平均值IL大于零和小于零的实验数据如表1，表2所示。

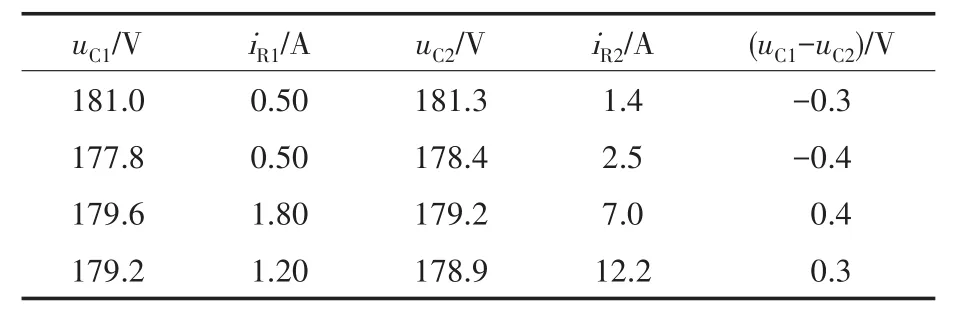
表1 电感电流平均值IL大于零实验数据Tab.1 Experimental data under ILabove zero

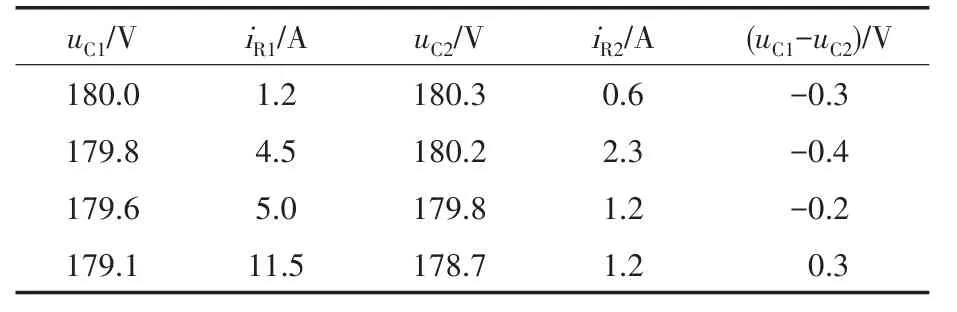
表2 电感电流平均值IL小于零实验数据Tab.2 Experimental data under ILabove zero

从表1和表2可以看出：在不同输入电压和负载情况下，单极性电流控制半桥电压平衡电路能够很好地实现输出电压均衡。

从仿真和实验结果也可以看出：在单极性电流控制方法下，当电感电流平均值大于零时，S1工作、S2不工作；反之，S2工作、S1不工作；由于电感电流是单极性的，所以在任何情况下输入和输出端之间都不存在无功电流流动问题；在负载突变时，也能够很好地实现输出电压均衡。

4 结论

半桥电压平衡电路结构简单、成本低，但是在互补驱动时，输入和输出端之间可能存在无功电流问题。因此，本文研究了一种半桥电压平衡电路单极性电流控制方法，从而实现半桥电压平衡电路中电感电流在任何情况下都能单极性运行，输入和输出端之间不存在无功电流。文中对其原理进行详细的分析。仿真和实验结果表明半桥电压平衡电路在电感电流单极性运行控制方法下能够很好地实现输出电压均衡功能。