双三相永磁同步电机模型预测电流控制研究

2021-03-23 03:49

电气传动 2021年6期

（上海大学机电工程与自动化学院，上海 200444）

随着电力电子技术、微控制器技术和电机控制理论的发展，以及工业应用场合的需求，多相电机及驱动系统以其低压大功率输出、高可靠性、低转矩脉动的特点吸引了越来越多的学者研究[1-3]。其中，双三相永磁同步电机驱动系统是当前研究热点之一。同时，模型预测电流控制技术具有结构简单、响应速度快、灵活度高的特点而受到人们广泛关注[4-7]。

模型预测电流控制（model predictive current control，MPCC）是一种通过衡量不同的电压矢量对电机状态产生的影响，筛选出下一时刻最优的工作电压矢量的控制策略。相比于矢量控制，MPCC取代了传统的比例积分（PI）控制器和脉宽调制器，避免了控制器参数整定和复杂计算的问题，并且具有更快的转矩响应能力[8]。MPCC的研究广泛应用于三相电机。对于三相电机而言，MPCC只需针对静止坐标系或者旋转坐标系下的电机离散数学模型，通过预测模型计算下一时刻的电流值，利用价值函数在线寻优得出最优电压矢量[9-11]。而对于六相电机，根据矢量空间解耦理论[12]，解耦变换后有三个不同的子平面，需要同时考虑两个子平面，即基波子平面和谐波子平面（零序子平面为0）。然而，只有基波子平面负责产生转矩，谐波子平面不参与机电能量转换，但该平面很小的电阻和漏感能够造成很大的谐波电流[13]。同时，六相电压源型逆变器产生的电压矢量在不同的子平面有不同的幅值和方向，这就大大地增加了设计预测控制系统的难度。

目前，对多相电机模型预测控制的研究并不多见。文献[14-15]对六相感应电机MPCC进行了研究，考虑了电压矢量个数和不同的价值函数对模型预测的影响，并讨论了实现该控制算法所需要的时间，证明MPCC策略在多相电机应用方面的有效性。文献[16]针对五相永磁同步电机提出一种虚拟电压矢量MPCC控制，充分利用电压矢量的特点，将虚拟矢量作为预测矢量，从而达到降低谐波电流的目的。文献[14-16]虽都实现了多相电机模型预测控制，且降低了谐波电流，但价值函数过于复杂，需要对权重系数整定，整定过程根据仿真实验结果反复调整，无疑会增加实验的复杂性。文献[17]运用多目标方式取代权重系数，通过建立两个价值函数，利用一个平均评价准则来选取使磁链、转矩误差都较小的电压矢量。文献[18]建立了一种自适应机制，运用两个价值函数，使转矩和磁链误差限制在初始界限内，从而消除了权重系数。文献[17-18]都是以三相电机为研究对象，六相电机比三相电机更为复杂，解耦后多一个谐波子平面，因此关于六相电机权重系数的问题需进一步研究。

文献[19]针对双三相永磁同步电机提出一种模型预测转矩控制策略，通过分析电压矢量在基波子平面和谐波子平面的方向和幅值，建立抑制谐波电流的开关表，新的开关表有效地抑制了谐波电流并降低了系统的计算量。文献[20]针对T型三电平双三相永磁同步电机驱动系统的共模电压，利用系统空间零共模电压矢量，显著抑制了系统共模电压，并很好地控制了电机电流。

为了抑制双三相永磁同步电机（dual three phase PMSM，DTP-PMSM）的谐波电流，并降低系统计算量。提出了一种改进的DTP-PMSM模型预测电流控制方法。通过在一个控制周期内选择作用两个电压矢量，即一个外围大矢量和一个次外围矢量，调整两个矢量的作用时间使z1z2子平面的平均电压幅值为零，从而实现谐波电流的抑制。对定子磁链进行观测，确定磁链所在扇区，将预测电压矢量个数由12个减少为8个，降低了系统的计算量。以αβ子平面的电流跟踪误差作为价值函数，消除了权重系数，选择出最优电压矢量。最后通过实验研究验证了该方案的有效性。

1 双三相永磁同步电机数学模型

图1为双三相永磁同步电机结构示意图。

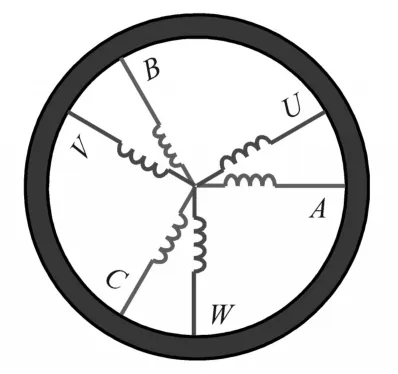
图1 双三相永磁同步电机结构Fig.1 Structure of double three phase permanent magnet synchronous motor

不同于六相对称永磁同步电机，DTP-PMSM的两套三相绕组采用互差30°的方式放置，并且两套绕组的中性点相互隔离，所以又称六相不对称电机。根据矢量空间解耦变换（vector space decompation，VSD），将双三相电机的所有分量映射到相互正交的αβ，z1z2及o1o23个子平面[12]，其中，αβ子平面为基波子平面，只有该平面分量参与机电能量转换，z1z2子平面为谐波子平面，该平面分量不对气隙磁通和转矩做贡献，o1o2子平面为零序子平面，由于中性点相互隔离，零序谐波分量不能流动，该平面分量为零。VSD变换矩阵为

然后利用旋转变换式，将静止坐标系转换到同步旋转坐标系。由于只有αβ子平面参与机电能量转换，所以无需考虑z1z2子平面、o1o2子平面。旋转变换式如下：

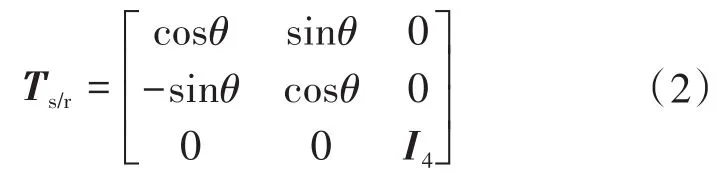
式中：θ为转子位置角度：I4为4维单位矩阵。

同步旋转坐标系下αβ子平面的数学方程为

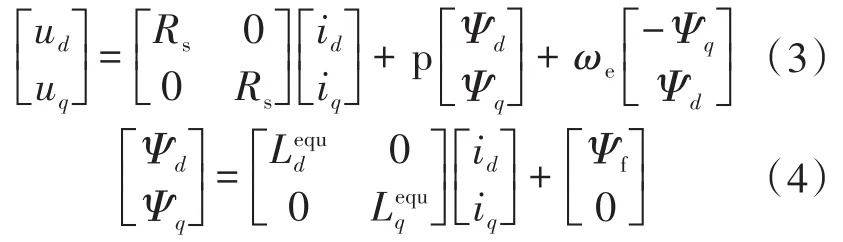
其中

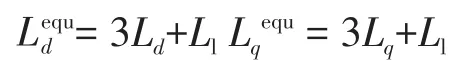
式中：ud，uq，id，iq，Ψd，Ψq为αβ子平面的定子电压、电流、磁链；p为微分算子；Rs为定子电阻；ωe为电角频率；Ψf为永磁体磁链；Lequd，Lequq分别为d，q轴电感；Ld，Lq分别为d，q轴主自感；Ll为定子绕组漏自感。

z1z2子平面的数学方程为

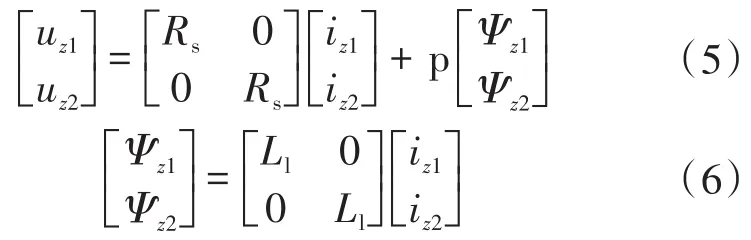
式中：uz1，uz2，iz1，iz2，Ψz1，Ψz2分别为 z1z2子平面的定子电压、电流、磁链。

电磁转矩方程为

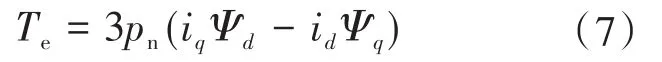
式中：Te为电磁转矩；pn为极对数。

2 模型预测电流控制

2.1 预测模型

首先，基于αβ子平面的双三相永磁同步电机数学模型，将磁链方程（4）代入电压方程（3），通过离散化处理得预测电流模型：

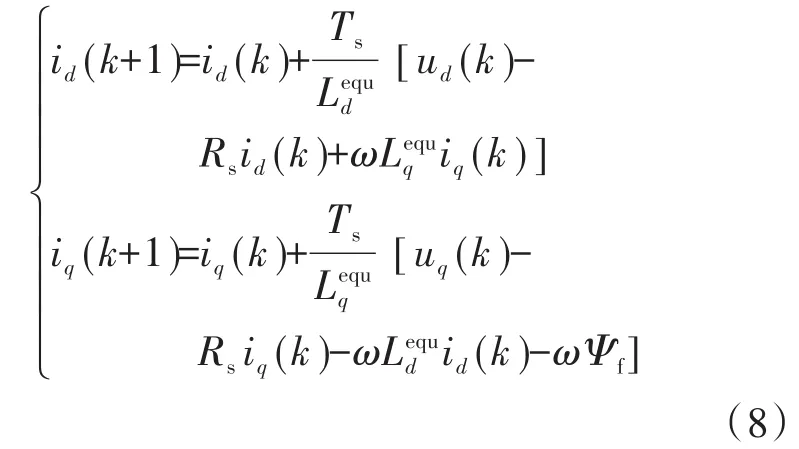
式中：id(k)，iq(k)，ud(k)，uq(k)为 k时刻的 d，q轴电流、电压值；id(k+1)，iq(k+1)为k+1时刻的d，q轴电流值。

同理可得z1z2子平面的预测电流模型，如下式所示：

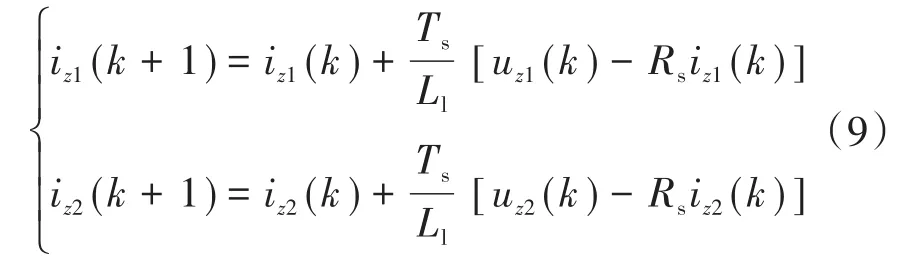
式中：iz1(k)，iz2(k)，uz1(k)，uz2(k)分别为 k时刻的z1z2子平面电流、电压值；iz1(k+1)，iz2(k+1)为 k+1时刻的z1z2子平面电流值。

2.2 选取电压矢量

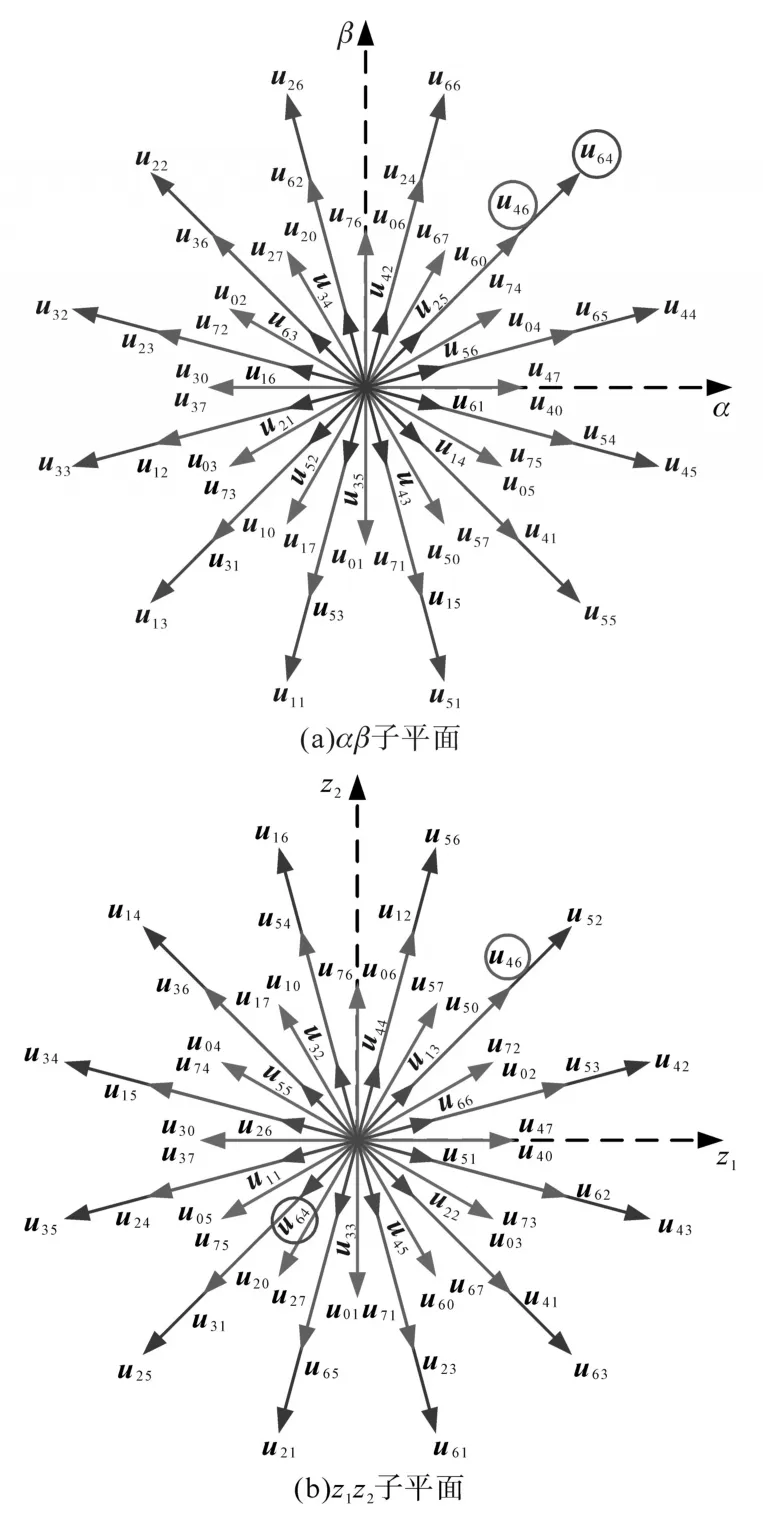
图2 六相逆变器电压矢量Fig.2 Voltage vectors of six-phase inverter

MPCC通过计算电压矢量作用于电机产生的电流值，选取最接近给定电流值的电压矢量作为最优电压矢量。将49个矢量全部代入预测方程进行计算，这种方式存在计算量大、效率低、谐波电流大等缺点。为了减小计算量、降低谐波电流，一般采用最外围12个大矢量作为预测电压矢量。然而最外围大矢量在谐波子平面具有一定的电压，会引起较大的谐波电流。本文将最外围大矢量和次外围中矢量相结合作为预测矢量，以实现最优电压矢量的选取和抑制谐波电流的目的。

如图2所示，最外围大矢量与次外围中矢量在αβ子平面方向相同，而在z1z2子平面则方向相反，如u64，u46。根据这个特性，可选择在一个控制周期内作用两个矢量，即一个大矢量和一个中矢量，通过调整它们的作用时间，使谐波子平面的平均电压幅值为零，如下式所示：

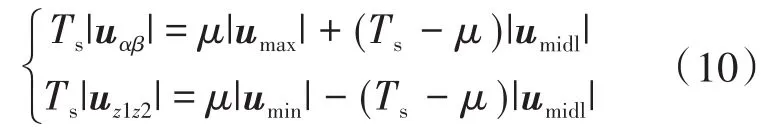
由两个子平面建立两个等式，第一个等式为αβ子平面的等式。依据伏秒积平衡原理，在一个控制周期Ts内，大矢量作用时间为μ，中矢量作用时间为（Ts-μ），等效的电压矢量幅值为|uαβ|。同理，第二个等式为z1z2子平面的等式，等效的电压幅值为|uz1z2|。

令|uz1z2|=0，解式（10）可得：

图3为预测电压矢量，一个大矢量和一个中矢量组成一组作为预测电压矢量，共12组。

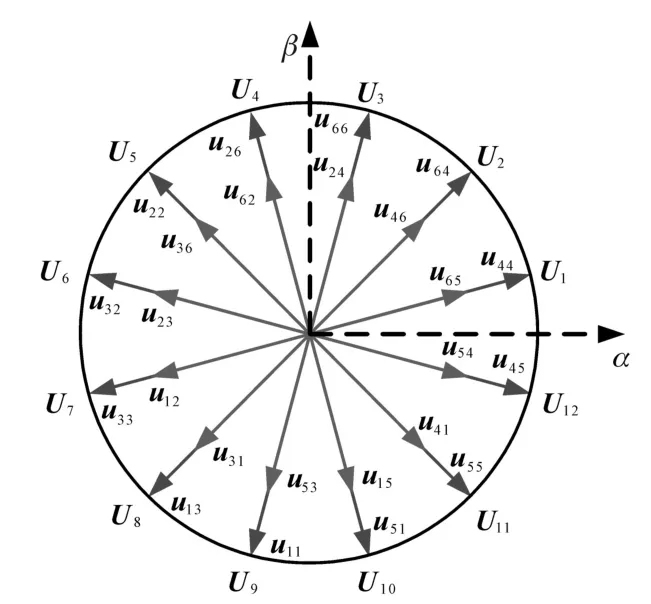
图3 预测电压矢量Fig.3 Predicted voltage vector

由式（11）可知，当选择一组电压矢量作用时，如 U2（u64，u46），让 u64作用 0.73Ts，u46作用0.27Ts，即可得到一个等效在αβ子平面幅值为0.596Udc、在z1z2子平面幅值为0的电压矢量。

2.3 减少预测电压矢量个数

由前文分析，MPCC选取12个预测电压矢量代入预测模型进行迭代计算，相比49个电压矢量，预测矢量已减少许多，但对于系统总的运算量依然较大，需要较久的计算时间。

为降低运算量，本文通过观测定子磁链位置，将预测电压矢量由12个减少到8个，实现减少计算时间的目的。

图4为预测电压矢量优化选择图。

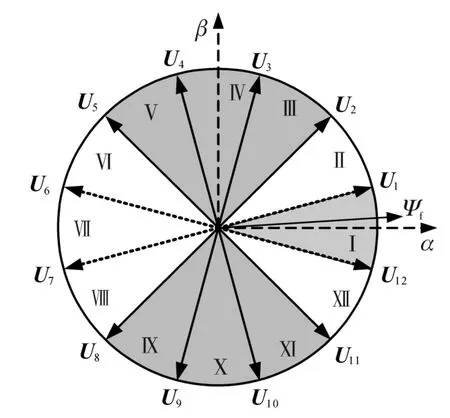
图4 预测电压矢量优化选择Fig.4 Optimal selection of predictived voltage vector

根据定子磁链所在扇区选择预测电压矢量，若定子磁链位于扇区Ⅰ，为避免电压矢量选取变化过大，降低电流波动，U6，U7与定子磁链方向相反，不作为预测电压矢量。同时希望电流具有快速的动态响应，预测矢量不考虑最接近扇区Ⅰ的两个矢量U1，U12，因此，仅需选择8个电压矢量，即 U2，U3，U4，U5，U8，U9，U10，U11作为预测电压矢量，从而减少预测电压矢量个数。

其它扇区的预测电压矢量可依次推理得出，在此不再赘述。

定子磁链利用VSD变换的定子电流iα，iβ以及转子的位置进行观测，将其带入下两式即可得到定子磁链所在位置θΨ。

2.4 价值函数

对于双三相永磁同步电机，MPCC一般以d，q轴电流跟踪差值与谐波电流值之和作为价值函数，如下式所示：

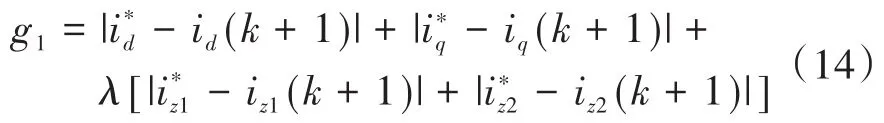
由于文章采用两个电压矢量抑制谐波电流，对于价值函数而言，无需添加谐波电流作为评价指标，只需通过d，q轴电流误差跟踪来选取最优的一组电压矢量作为价值函数，如下式所示：

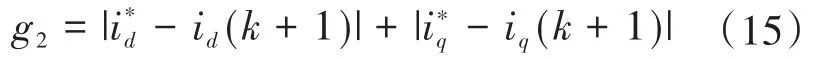
双三相永磁同步电机模型预测电流控制系统框图如图5所示。

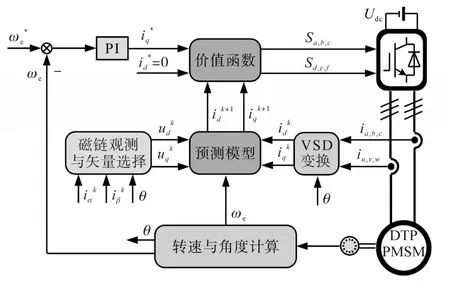
图5 双三相永磁电机模型预测电流控制系统框图Fig.5 Block diagram of model predictive current control system for DTP-PMSM

控制方法如下：

3）利用价值函数式（15）在线寻优，筛选出使d，q轴电流跟踪误差最小的电压矢量，将其作为最优电压矢量。

4）将最优的电压矢量作用于电机。

3 实验研究

实验研究所用的双三相永磁同步电机控制系统平台配置，如图6所示。

图6 实验系统配置Fig.6 Experimental system configuration

其中，控制系统采用的微控制器为TMS320F2812，双三相永磁同步电机功率为5.5 kW，对拖一台直流发电机作为负载，电机参数如下：额定功率5.5 kW，额定电压380 V，额定电流4.6 A，定子电阻1.52 Ω，d轴电感12.0 mH，q轴电感42.0 mH，永磁体磁链0.585 Wb，极对数为3，额定转速1 500 r/min，系统采样频率5 kHz，直流母线电压Udc为540 V。

实验研究中首先对只使用最外围大矢量的模型预测电流控制算法进行了验证，此处简称为MPCC1。然后进一步地采用最外围大矢量和次外围中矢量相结合的模型预测电流控制算法对电机进行控制，简称MPCC2。为了使MPCC1与MPCC2在同一个采样控制的周期下进行比较，MPCC1也使用8个预测电压矢量进行控制。

图7为转速100 r/min下MPCC1控制的电流波形。图7a为整体电流波形，负载为20 N·m，加减载前后相电流波形未有明显变化。分别观察空载与加载时电流运行放大波形，如图7b所示，电机空载运行时，A，U相电流并不为零，并且有效值较大为9 A，同时谐波子平面的电流iz1，iz2有效值也在9 A左右，其原因在于双三相电机的谐波子平面阻抗很小，即便较小的电压也将会引起很大的谐波电流，iz1，iz2幅值高，导致通过双三相电机的相电流过大。从图7c带载运行结果看出，相电流幅值较空载时未有明显增加，且电流波形严重畸变，原因在于谐波电流的幅值很大，增加的基波电流不足以使相电流产生明显变化。

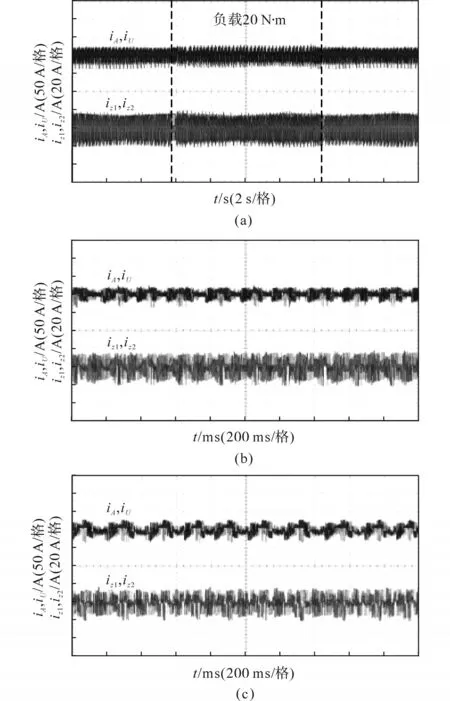
图7 转速100 r/min的相电流与谐波电流波形（MPCC1）Fig.7 Waveforms of phase current and harmonic current at 100 r/min（MPCC1）

图8给出了转速300 r/min下MPCC1加减载运行结果。观察发现，在突加60%额定负载，负载转矩为20 N·m，转速略有波动，能够保持给定转速运行，但存在较大的转矩波动，同时相电流在加减载前后未有明显变化，电流有效值约10 A。从图8b稳态结果看到，相电流波形严重畸变，主要原因如前所述，谐波电流含量过大，使得相电流不能反映基波电流的变化，转矩波动10 N·m左右，电机运行效果较差。

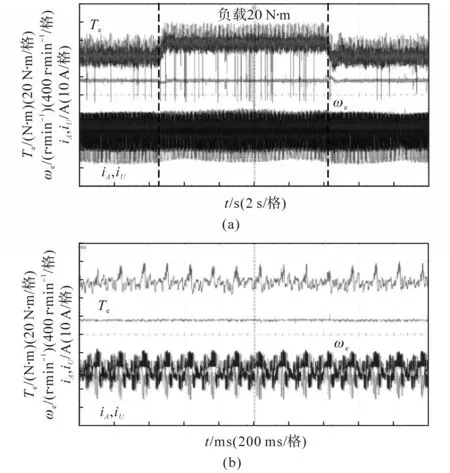
图8 转速300 r/min的负载转矩突增与突减运行结果（MPCC1）Fig.8 Operation results of sudden load increase and reduction at 300 r/min（MPCC1）

图9为MPCC2运行的加减载工作波形。

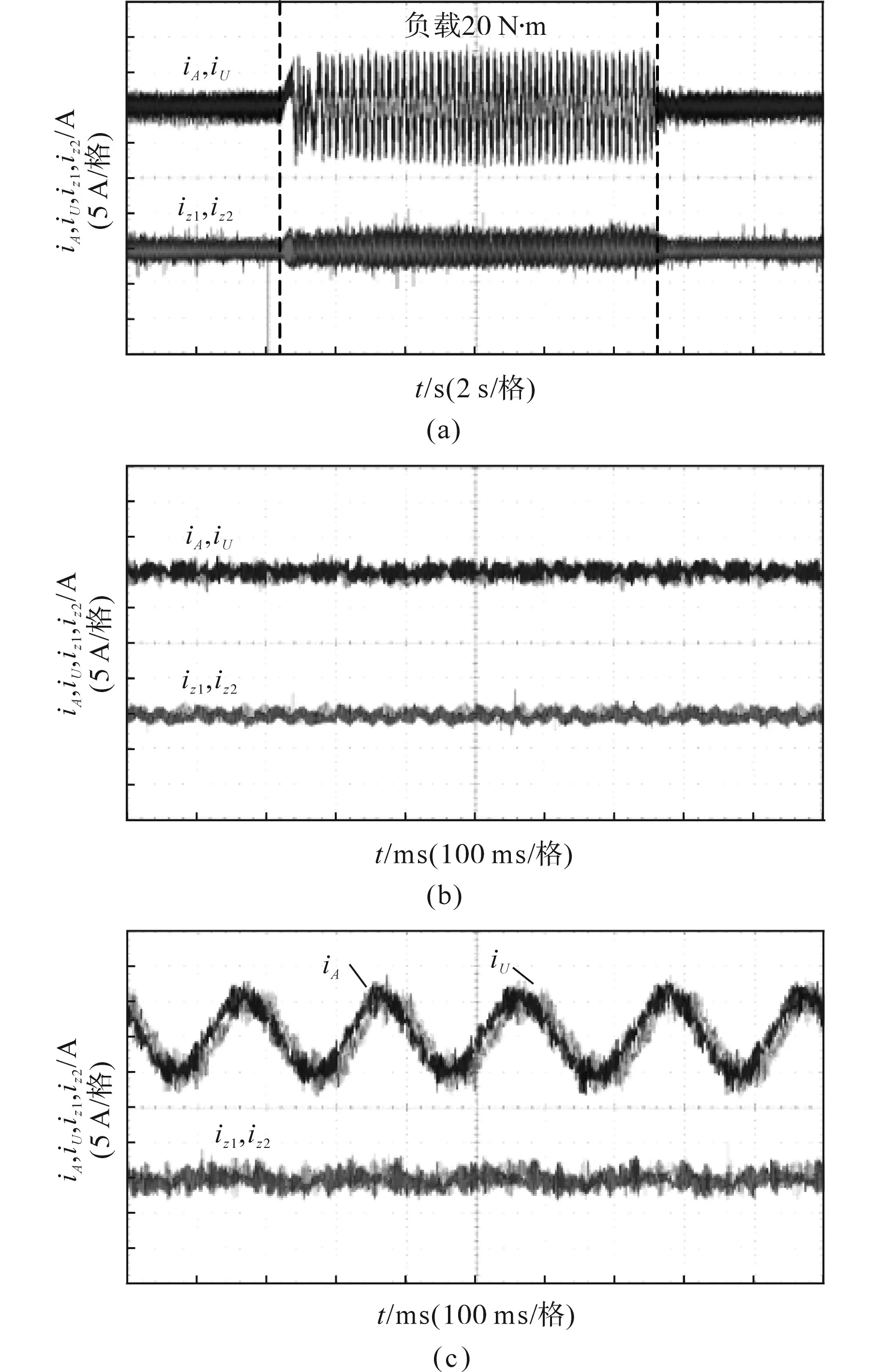
图9 转速100 r/min的相电流与谐波电流波形（MPCC2）Fig.9 Waveform of phase current and harmonic current at 100 r/min （MPCC2）

图9a为整体电流波形，负载为20 N·m，可以看出，电流的幅值在加减载前后有明显变化。图9b为电机空载情况下的相电流与谐波电流，谐波电流有效值约1 A，与未加谐波抑制算法的谐波电流相比，有显著的抑制效果。图9c为电机带60%额定负载运行结果，相电流有效值达到4.0 A，电流波形正常，体现了MPCC2在基波子平面的良好控制效果。

图10为不同转速情况下双三相电机MPCC2的稳态运行实验结果，负载转矩20 N·m。由图10可以看出，不同转速情况下，转矩波动在上下2 N·m，同时转速保持平稳，在不同转速情况下稳定带载运行。

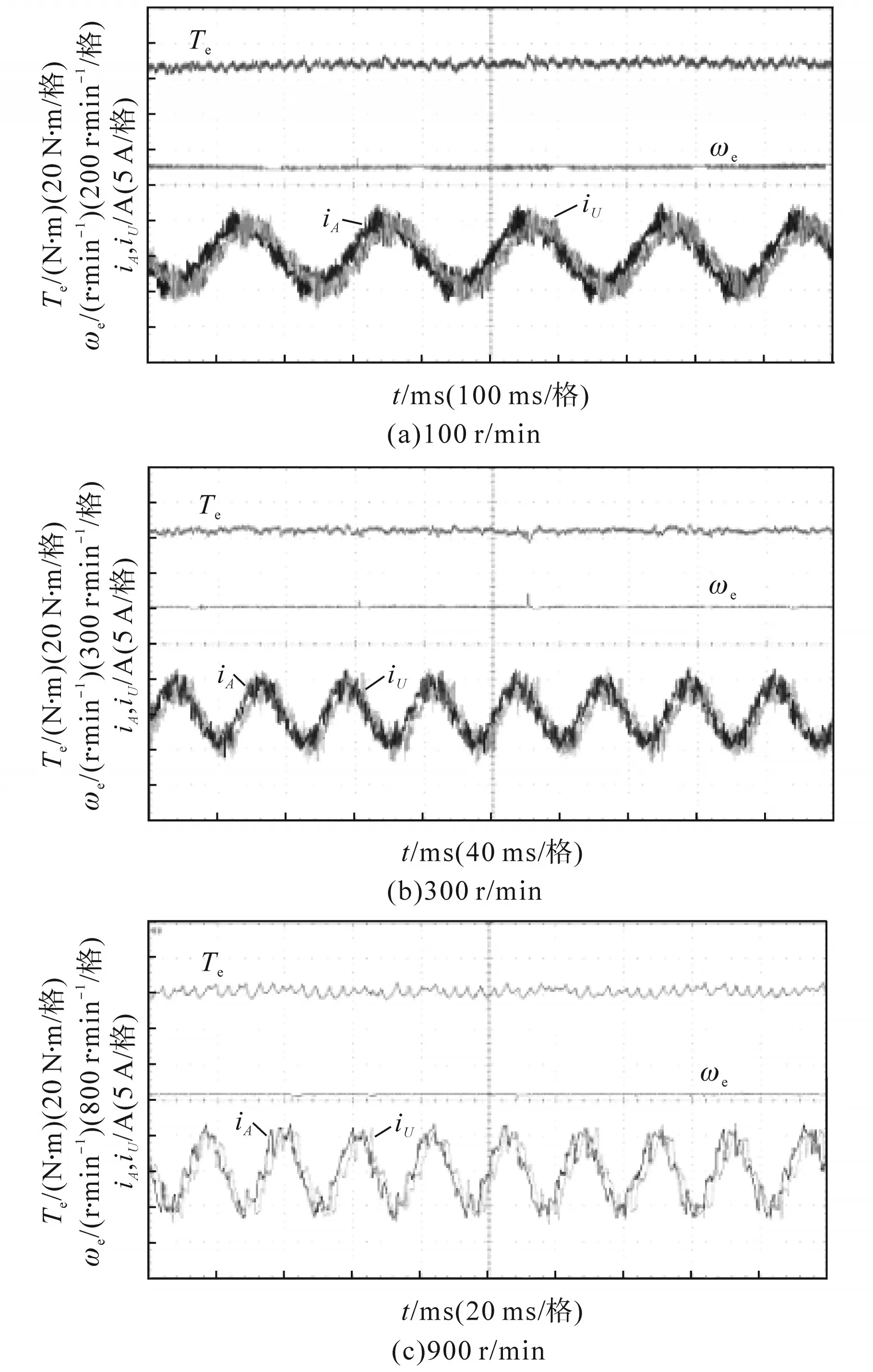
图10 双三相电机稳态运行结果（MPPC2）Fig.10 Steady state operation results of dual three phase motor（MPPC2）

图11给出了转速900 r/min时，电机突加与突减负载动态性能实验结果。由图11可以看出，电机转矩在负载突变时能够快速响应，对动态中的转速变化响应迅速，电机运行状态良好。

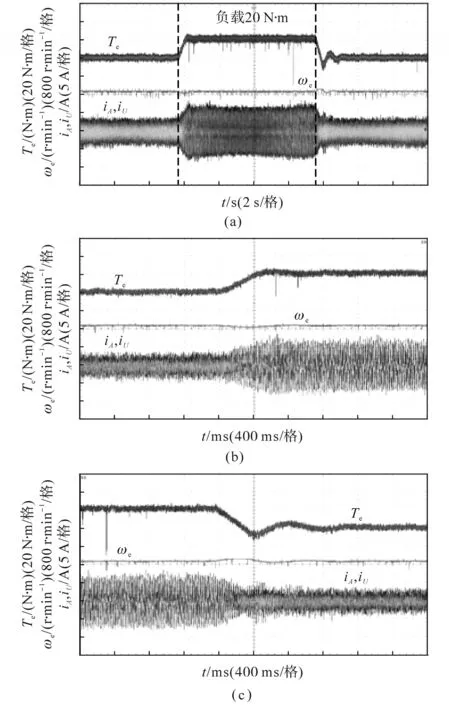
图11 电机负载突变的动态性能波形Fig.11 Dynamic performance waveforms of motor with sudden load change

4 结论

本文研究了DTP-PMSM驱动系统的模型预测电流控制策略，采用两个电压矢量相结合的方法，根据定子磁链位置选取预测电压矢量，无需将每个电压矢量代入预测模型计算，最终通过实验研究对模型预测电流控制算法进行了验证，得到如下结论：

1）传统的模型预测电流控制仅采用最外围电压大矢量作用于电机，虽然谐波子平面的平均电压值小，但该平面具有很小的阻抗，能够引起较大的谐波电流，使得相电流幅值过大，不能正常运行。

2）利用最外围大矢量与次外围中矢量在谐波子平面方向相反的特性，每个采样周期选择两个电压矢量作用于电机，使得谐波子平面的平均电压幅值为零，可以有效抑制双三相电机的谐波电流。

3）根据定子磁链所在扇区选择预测电压矢量，可将12个预测电压矢量减少至8个，预测矢量减少后的控制算法运行稳定，具有良好的稳态和动态性能。

实验结果验证了所研究控制方案的有效性和可行性。