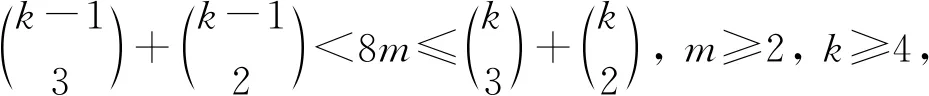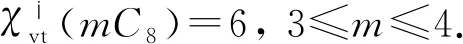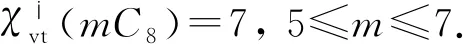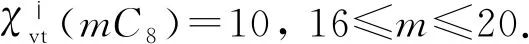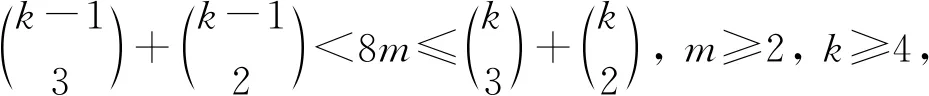图mC8的点可区别Ⅰ-全染色和Ⅵ-全染色

杨 晗,陈祥恩

(西北师范大学 数学与统计学院,兰州 730070)

1 引言与预备知识

本文所考虑的图均为有限无向简单图. 目前,关于图的点可区别正常边染色与图的点可区别一般边染色研究已有很多结果[1-9].

设f:V∪E→{1,2,…,k}为图G的一个全染色(正常或未必正常). 对图G的每个顶点x,用Cf(x)表示在f下点x的颜色及全体与x关联的边的颜色构成的集合(非多重集),称其为x的色集合或调色板. 设f为图G的一个正常全染色. 若对∀u,v∈V,u≠v,总有C(u)≠C(v),则称f为G的点可区别全染色(VDTC)[10-11]. 本文考虑图的点可区别的一类未必正常的全染色.

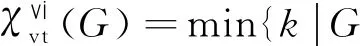
用ni(G)表示图G的度为i的顶点个数,δ≤i≤Δ,这里δ和Δ分别表示图G的最小度和最大度. 记

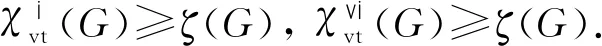
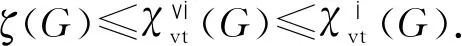
由于图的点可区别Ⅰ-全染色必为图的点可区别Ⅵ-全染色,故本文只讨论图的点可区别Ⅰ-全染色,相应的图的点可区别Ⅵ-全染色由此可得.

文献[12]提出了图的点可区别Ⅰ-全染色及图的点可区别Ⅵ-全染色,并确定了完全图、完全二部图、轮、扇、正规双星、路、圈、两条同阶圈的联图、一类近完全图等图类的点可区别Ⅰ-全色数以及点可区别Ⅵ-全色数,并提出了下列猜想.

文献[14-16]研究了两条路的联图、圈与路的联图、圈与圈、圈与轮、圈与扇的联图的点可区别Ⅰ-全染色和Ⅵ-全染色. 文献[17]研究了m个长为4的圈不交并mC4的点可区别全染色. 本文构造m个长为8的圈不交并mC8的最优点可区别Ⅰ-全染色,并确定mC8的点可区别Ⅰ-全色数,当m≥2时,即为ζ(G). 利用命题1确定当m≥2时,mC8的点可区别Ⅵ-全色数. 结果表明,VDITC 猜想和VDVITC猜想对图mC8成立.

首先,对任意的k≥6,构造(k-1)×(k-1)阶矩阵Ak,使矩阵Ak的元素是集合{1,2,…,k}的含k的2-子集、3-子集(是即将构造出的某个VDITC下点的色集合,这里的集合不是多重集)或空集,其中第i行含有(i-1)个Ø:

(1)

定义1[17]设1≤i1

图1 C8的全染色Fig.1 Total colorings of C8

定义2[17]如果矩阵Ak的8个元素(非空)恰是在C8的某个点可区别Ⅰ-全染色下C8的全体顶点色集合,则称由这8个元素构成的组是好组.

定义3[17]如果矩阵Ak的4×2阶子矩阵B中的诸元素恰是在C8的某个点可区别Ⅰ-全染色下C8的8个顶点的色集合,则称子矩阵B是好的.

将如图1所示的8阶圈全染色记为a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,a. 在该染色下,边的色下方均有波浪线,而点的色下方没有波浪线.

引理1当i≡1(mod 4),j≡1(mod 2),且Ak(i,i+1,i+2,i+3|j,j+1)中元素都不是空集时,则Ak(i,i+1,i+2,i+3|j,j+1)为一个好的4×2阶子矩阵.

证明: 当i=1时,有

(2)

显然{k,j},{k,j+1},{k,j,j+1},{k,j,j+2},{k,j,j+3},{k,j+1,j+2},{k,j+1,j+3},{k,j+1,j+4}是C8的点可区别Ⅰ-全染色顶点的色集合,其染色为k,j+1,j,k,k,j,k,j+2,j+1,k,j,j+3,k,j+1,j+4,k,k. 于是当i=1时,Ak(i,i+1,i+2,i+3|j,j+1)是一个好的子矩阵.

当i≥5时,有

(3)

显然{k,j,j+i-1},{k,j+1,j+i},{k,j,j+i},{k,j,j+i+1},{k,j,j+i+2},{k,j+1,j+i+1},{k,j+1,j+i+2},{k,j+1,j+i+3}是C8的点可区别Ⅰ-全染色顶点的色集合,其染色为k,j+i,j+1,k,j+i+3,j+1,k,j+i+2,j,k,j+1,j+i+1,j,k,j+i-1,j,k. 于是当i≥5时,Ak(i,i+1,i+2,i+3|j,j+1)是一个好的子矩阵. 证毕.

由上述证明可知,一个好的子矩阵的所有元素可构成1个好组,它是C8在一种点可区别Ⅰ-全染色下顶点的色集合.

定义4[17]如果矩阵Ak的元素既不是引理1中好的4×2阶子矩阵中的元素,也不是空集,则称该元素是Ak的剩余元素.

定义5[17]对mC8的一个k-VDITCf,如果{1,2,…,k}的所有2-子集(分别的,3-子集)均为在f下mC8的顶点色集合,则称2-子集(分别的,3-子集)在f下用完了.

下面给出C8点可区别Ⅰ-全染色的几种类型:

1) 类型1的染色为k-2,k-2,k-1,k,k-5,k-1,k-6,k,k-3,k-1,k,k,k-2,k-3,k,k,k-2. 在该染色下,C8顶点的色集合分别为{k,k-3},{k,k-2},{k,k-1},{k,k-3,k-2},{k,k-3,k-1},{k,k-2,k-1},{k,k-5,k-1},{k,k-6,k-1}.

2) 类型2的染色为k-3,k-3,k,k-2,k-2,k,k-3,k-1,k,k-4,k-2,k,k-3,k-4,k,k,k-3. 在该染色下,C8顶点的色集合分别为{k,k-4},{k,k-3},{k,k-2},{k,k-4,k-3},{k,k-4,k-2},{k,k-4,k-1},{k,k-3,k-2},{k,k-3,k-1}.

3) 类型3的染色为j+2,k-2,j,k,k-2,j+1,k,k-1,j,k,j+1,k-3,k,j,k-4,k,j+2. 在该染色下,C8顶点的色集合分别为{k,j,k-4},{k,j,k-3},{k,j,k-2},{k,j,k-1},{k,j+1,k-3},{k,j+1,k-2},{k,j+1,k-1},{k,j+2,k-2}.

4) 类型4的染色为a,k-1,b,k,c,k-1,d,k,e,k-1,f,k,g,k-1,k,k,a. 在该染色下,C8顶点的色集合分别为{k,k-1},{k,a,k-1},{k,b,k-1},{k,c,k-1},{k,d,k-1},{k,e,k-1},{k,f,k-1},{k,g,k-1}.

5) 类型5的染色为a,k-1,b,k,c,k-1,d,k,e,k-1,f,k,g,k-1,h,k,a. 在该染色下,C8顶点的色集合分别为{k,a,k-1},{k,b,k-1},{k,c,k-1},{k,d,k-1},{k,e,k-1},{k,f,k-1},{k,g,k-1},{k,h,k-1}.

6) 类型6的染色为k-2,j+1,k,k-1,j+2,k,k-1,j+4,k,k-2,j+5,k,j+4,k-3,j,k,k-2. 在该染色下,C8顶点的色集合分别为{k,j,k-3},{k,j+1,k-2},{k,j+1,k-1},{k,j+2,k-1},{k,j+4,k-3},{k,j+4,k-2},{k,j+4,k-1},{k,j+5,k-2}.

7) 类型7的染色为k-2,j+4,k,k-1,j+2,k,k-2,j+1,k,k-1,j,k,k-2,j,k-3,k,k-2. 在该染色下,C8顶点的色集合分别为{k,j,k-3},{k,j,k-2},{k,j,k-1},{k,j+1,k-2},{k,j+1,k-1},{k,j+2,k-1},{k,j+4,k-2},{k,j+4,k-1}.

8) 类型8的染色为j+1,k-1,j+5,k,k-2,j+4,k-1,k,k-2,j+3,k-3,k,j+3,k-1,j,k,j+1. 在该染色下,C8顶点的色集合分别为{k,j,k-1},{k,j+1,k-1},{k,j+3,k-3},{k,j+3,k-2},{k,j+3,k-1},{k,j+4,k-1},{k,j+4,k-2},{k,j+5,k-1}.

9) 类型9的染色为j,k-2,k,j+3,k-3,k,j+3,k-1,k,j+4,k-2,k,j+5,k-1,j+1,k,j. 在该染色下,C8顶点的色集合分别为{k,j,k-2},{k,j+1,k-1},{k,j+3,k-3},{k,j+3,k-2},{k,j+3,k-1},{k,j+4,k-1},{k,j+4,k-2},{k,j+5,k-1}.

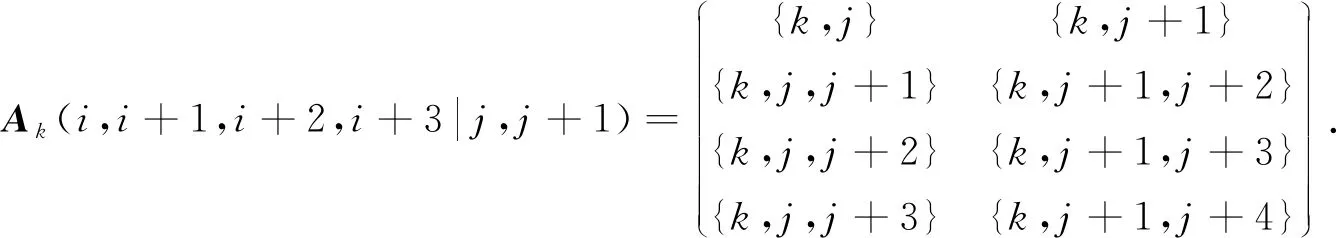
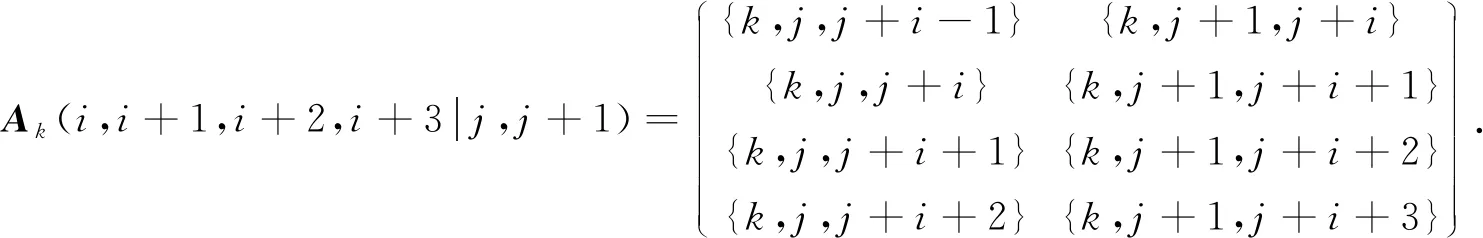
2 主要结果

由命题1可得: