基于非负最小二乘法的全色与高光谱图像融合

郝红勋 何红艳 张炳先

基于非负最小二乘法的全色与高光谱图像融合

郝红勋1何红艳2,3张炳先2,3

（1 中国民航大学飞行技术学院，天津 300300）（2 北京空间机电研究所，北京 100094）（3 先进光学遥感技术北京市重点实验室，北京 100094）

现有光学遥感图像融合方法主要针对全色与多光谱图像，直接将其用于全色与高光谱图像融合存在以下问题：高光谱图像波段数量远多于多光谱图像，通过高光谱波段加权合成低分辨率全色图像，容易出现灰度失真；高光谱图像与全色图像的空间分辨率相差很大，采用现有的加性变换融合方法，会导致融合图像中部分地物出现光谱或细节失真。为此，文章提出了基于非负最小二乘法的全色与高光谱图像融合方法。首先对高光谱图像进行波段压缩，得到波段压缩的高光谱图像；然后对波段压缩的高光谱图像及全色图像进行非负最小二乘拟合，得到低分辨率全色图像；最后，采用比值变换模型生成融合图像。试验表明该方法的光谱与细节保真效果好，优于对比方法。

图像融合 高光谱图像 非负最小二乘 遥感图像 航天遥感

0 引言

目前，越来越多的航天平台采用全色与高光谱传感器同时相对地成像，如美国的Earth Observing-1（EO-1）卫星，以及我国的“天宫一号”（TG-1）目标飞行器等。对于同时相成像方式，其全色图像的空间分辨率远优于高光谱图像，原因在于：全色传感器探元接收入射光的光谱范围远比高光谱传感器探元宽，若要接收相同能量的入射光，高光谱传感器探元的物理尺寸远大于全色传感器探元[1]；此外，高空间分辨率的高光谱传感器数据形成率极大，会给星地数据传输带来极大的压力。但是，实际应用往往需要高空间分辨率的高光谱图像，因此，遥感图像融合技术一直以来是遥感图像预处理的关键技术，至今依然是数据融合领域的研究热点[2]。

光学遥感图像融合主要针对全色与多光谱图像，可分为加性变换和比值变换两大类型[3]。比值变换（Ratio Transformation，RT）融合方法[4-6]，首先计算全色图像及其对应低分辨率全色图像的比值图像，该比值图像主要表征融合图像的空间细节；然后按像素点计算比值图像与多光谱上采样图像的乘积生成融合图像。加性变换进一步分为分量替换（Component Substitution，CS）、频率域变换（Frequency Transformation，FT）两类。分量替换法[7-11]首先对多光谱图像进行矩阵变换，得到保留分量和替换分量；然后对全色图像与保留分量进行矩阵逆变换生成融合图像。频率域变换融合方法[12-13]首先分别对全色与多光谱图像进行频率分解；然后通过全色图像的高频分量及多光谱图像的低频分量的逆变换生成融合图像。总体而言，加性变换融合方法难以克服多光谱图像过饱和引起的光谱和细节失真[3, 5]，且计算复杂度高于比值变换融合方法，因此这类方法研究较多但实用性较差。

迄今为止，针对高光谱图像的融合方法研究相对较少，其中，文献[14-15]主要采用加性变换实现多光谱与高光谱图像融合，该类方法不适用于全色与高光谱图像融合。文献[16]采用比值变换实现全色与高光谱图像融合，其高光谱波段合并与低分辨率全色图像合成实际应用需要人工调节参数，否则融合图像容易出现光谱失真。文献[17-18]采用加性变换实现全色与高光谱图像融合，计算复杂度高，且存在光谱与细节失真问题。全色与高光谱图像融合与全色与多光谱图像融合存在较大差异，主要表现在：1）高光谱图像波段数量多，而多光谱图像波段数量相对较少，二者甚至相差几十倍，导致利用高光谱波段合成低分辨率全色图像更容易出现灰度失真；2）一般而言，全色与高光谱图像的空间分辨率差异远大于全色与多光谱图像的空间分辨率差异，导致融合图像容易出现细节失真。因此，将全色与多光谱图像的融合方法直接应用于全色与高光谱图像，容易产生光谱与细节失真问题。针对上述问题，本文提出了波段合并策略和基于非负最小二乘法的低分辨率全色图像合成策略，从而实现全色与高光谱图像的高保真融合。

1 全色与高光谱图像的高保真融合

高光谱图像波段数量多，直接利用高光谱波段合成低分辨率全色图像容易产生灰度失真，因此利用自适应均值加权技术将相邻的多个高光谱波段加权合成为一个波段，得到合并波段图像，可有效减少低分辨率全色图像合成所使用的高光谱波段数量；另外，不同地物反射光谱差异较大，且无约束最小二乘拟合未考虑高光谱波段对合成低分辨率全色图像权值的非负性，也导致合成的低分辨率全色图像出现灰度失真，需要对全色与合并波段图像的像元进行自适应聚类，并对不同类别像元采用非负最小二乘拟合低分辨率全色图像；最后，采用比值变换法，生成光谱与细节高保真的全色与高光谱融合图像。总体技术路线见图1。

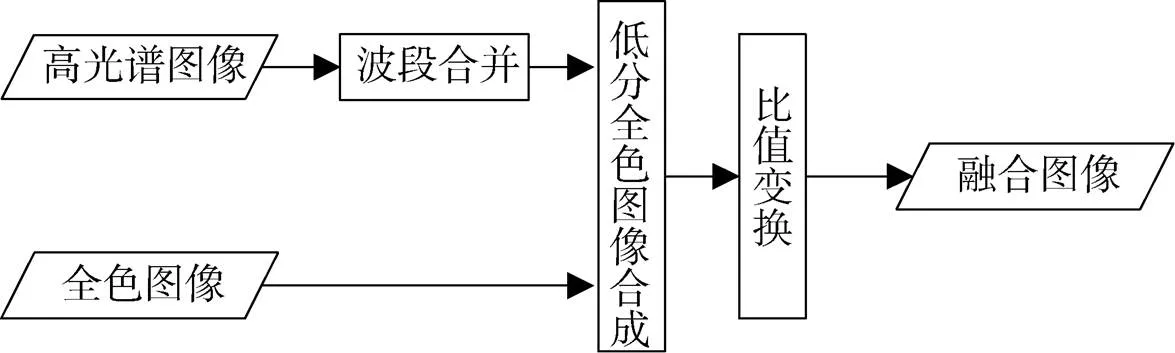
图1 总体技术路线

1.1 高光谱图像波段合并

高光谱图像波段合并的主要原因在于：1）利用最小二乘拟合低分辨率全色图像时，使用的高光谱图像波段越多，生成的低分辨率全色图像越容易产生光谱失真；2）高光谱图像波段数量多，直接利用高光谱图像的所有波段拟合生成低分辨率全色图像计算耗时多。因此，本文设计了自适应均值加权策略，将全色波段所涵盖的高光谱波段归并为少量的合并波段，可有效避免文献[16]中的人为指定波段合并步长对不同类型高光谱图像适应性差的问题。

令全色波段所涵盖的高光谱波段为b，表示波段；，分别表示像元的行与列，则高光谱波段合并算法步骤如下：

1）波段合并初始步长=3；

2）将b中每相邻的个波段采用均值加权合并为一个波段，即

3）计算合并波段与高光谱图像波段的偏差

式中，分别为高光谱图像的每个波段总行数与列数；为高光谱图像总的波段数。

在步骤1）中，由于高光谱相邻波段中各像元的取值差异较小，为减小计算耗时，因此将初始步长设置为3。

1.2 低分辨率全色图像合成

低分辨率全色图像合成是全色与高光谱图像融合的关键环节，其生成的低分辨率全色图像直接影响融合图像的光谱和细节保真度。由于不同地物反射光谱差异较大，直接将所有地物视为一个整体拟合低分辨率全色图像时，部分地物容易出现灰度失真，进而导致其在融合图像中出现光谱失真，因此本文根据全色图像与合并波段的像元值相关性差异，将所有像元自适应聚类为不同类别；同时，无约束最小二乘拟合未考虑高光谱波段对合成低分辨率全色图像权值的非负性，可导致合成的低分辨率全色图像出现灰度失真，需要对不同类别像元进行非负最小二乘拟合，生成灰度高保真的低分辨率全色图像。

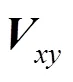
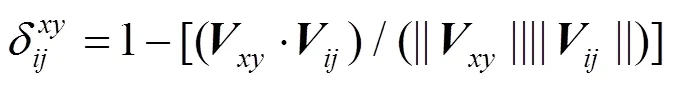
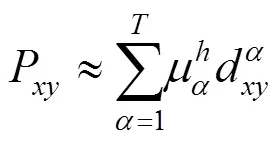
1.3 比值变换融合模型

加性变换法通过将全色图像的空间细节信息叠加至高光谱图像来生成融合图像，因此，当高光谱地物过饱和时，叠加空间细节信息产生饱和溢出，导致过饱和地物产生细节失真。为了避免该问题，采用比值变换融合模型生成全色与高光谱融合图像。

2 融合试验与分析

2.1 试验数据与评价指标

2.2 试验结果分析

文献[16-18]分别采用比值变换、频率变换、分量替换三种方法实现全色与高光谱图像融合，是当前最新发表的图像融合方法。将这三种方法与本文方法进行对比分析，试验结果如图2和图3所示。

（a）高光谱图像（a）Hyperspectral image（b）全色图像（b）Panchromatic image（c）分量替换法（c）CS method （d）频率变换法（d）FT method（e）比值变换法（e）RT method（f）本文方法（f）Our Method

（a）高光谱图像（a）Hyperspectral image（b）全色图像（b）Panchromatic image（c）分量替换法（c）CS method （d）频率变换法（d）FT method（e）比值变换法（e）RT method（f）本文方法（f）Our Method

通过对比高光谱图像与融合图像的色彩可发现，分量替换法、频率变换法、比值变换法生成的融合图像存在一定程度的光谱失真，而本文方法融合图像的光谱与细节保真效果均较好。表1给出了融合图像的客观评价值，可知本文方法在光谱保真、细节保真，以及综合保真三个方法均优于对比方法。

>

表1 图像融合质量定量评价

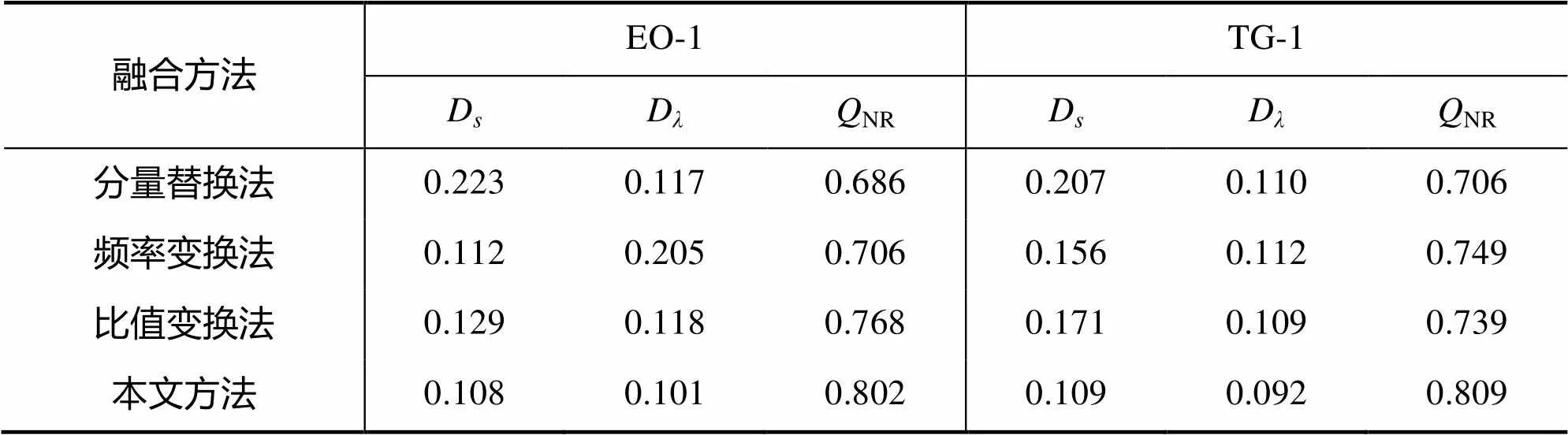
Tab.1 Quantitative evaluation of image fusion quality

3 结束语

本文提出了基于非负最小二乘法的全色与高光谱图像融合方法，其采用波段自适应合并、像元自适应分类以及非负最小二乘法准确合成低分辨率全色图像，提高了融合方法对不同类型地物、不同类型高光谱图像的适应性。美国EO-1卫星和我国TG-1目标飞行器的全色与高光谱图像融合试验表明，本方法的光谱与细节保真效果好，优于其他对比方法。需要指出的是，本文在合成低分辨率全色图像时，仅加入了非负约束，后续将进一步引入权值之和等于1的更强约束，以进一步提高融合图像的光谱与细节保真度。

)

[1] POHL C, GENDEREN V J L. Multisensor Image Fusion in Remote Sensing: Concepts, Methods, and Applications[J]. Remote Sensing, 1998, 19(5): 823-854.

[2] ZHANG J. Multi-source Remote Sensing Data Fusion: Status and Trends[J]. Image and Data Fusion, 2010, 1(1): 5-24.

[3] XU Q, ZHANG Y, LI B. Recent Advances in Pansharpening and Key Problems in Applications[J]. Image Data Fusion, 2014, 5(3): 175-195.

[4] ZHANG Y. System and Method for Image Fusion[P]: US7340099B2. 2008.

[5] XU Q, ZHANG Y, LI B, et al. Pansharpening Using Regression of Classified MS and Pan Images to Reduce Color Distortion[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 28-32.

[6] 徐其志, 高峰. 基于比值变换的全色与多光谱图像高保真融合方法[J]. 计算机科学, 2014, 41(10): 19-22. XU Qizhi, GAO Feng. Panchromatic and Hyperspectral Image High-fidelity Fusion Method Based on Ratio Transformation[J]. Computer Science, 2014, 41(10): 19-22. (in Chinese)

[7] XU Q, LI B, ZHANG Y, et al. High-fidelity Component Substitution Pansharpening by the Fitting of Substitution Data[J]. IEEE Transaction on Geoscience and Remote Sensing, 2014, 52(11): 7380-7392.

[8] 潘瑜, 徐丽燕, 王静, 等. 基于多重集典型相关分析的图像融合方法[J]. 航天返回与遥感, 2011, 32(3): 69-76. PAN Yu, XU Liyan, WANG Jing, et al. A Image Fusion Method Based on Multi-set Canonical Correlation Analysis[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(3): 69-76. (in Chinese)

[9] SHAHDOOSTI HR, GHASSEMIAN H. Combining the Spectral PCA and Spatial PCA Fusion Methods by an Optimal Filter[J]. Information Fusion, 2016, 27(1): 150-160.

[10] YANG Y, WU L, HUANG S, et al. Compensation Details-based Injection Model for Remote Sensing Image Fusion[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(5): 734-738.

[11] KHADEMI G, GHASSEMIAN H. Incorporating an Adaptive Image Prior Model into Bayesian Fusion of Multispectral and Panchromatic Images[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(6): 917-921.

[12] YANG Y, WAN W, HUANG S, et al. Remote Sensing Image Fusion Based on Adaptive IHS and Multiscale Guided Filter[J]. IEEE Access, 2016, 4: 4573-4582.

[13] JIN B, KIM G, CHO N. Wavelet-domain Satellite Image Fusion Based on A Generalized Fusion Equation[J]. Applied Remote Sensing. 2014, 8(1): 080599.

[14] NEZHAD Z D, KARAMI A, HEYLEN R, et al. Fusion of Hyperspectral and Multispectral Images Using Spectral Unmixing and Sparse Coding[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2377-2389.

[15] ZHOU Y, FENG L, HOU C, et al. Hyperspectral and Multispectral Image Fusion Based on Local Low Rank and Coupled Spectral Unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5997-6009.

[16] XU Q, QIU W, LI B, et al. Hyperspectral and Panchromatic Image Fusion Through an Improved Ratio Enhancement[J]. Journal of Applied Remote Sensing, 2017, 11(1): 1-14.

[17] AN Z, SHI Z. Hyperspectral Image Fusion by Multiplication of Spectral Constraint and NMF[J]. Optik-international Journal for Light and Electron Optics, 2014, 125(13): 3150-3158.

[18] LICCIARDI G A. Fusion of Hyperspectral and Panchromatic Images Using Multiresolution Analysis and Nonlinear PCA band reduction[J]. EURASIP Journal of Advance Signal Process, 2012(1): 1-17.

[19] ALEX R, ALESSANDRO L. Clustering by Fast Search and Find of Density Peaks[J]. Science, 2014, 344(6191): 1492-1496.

[20] 常璐, 廖安平. 基于罚函数的非负最小二乘问题的数值方法[EB/OL]. 北京: 中国科技论文在线[2018-05-21]. http://www.paper.edu.cn/releasepaper/content/201805-178. CHANG Lu, LIAO Anping. An Algorithm for Non-negative Least Squares Problem Based on Penalty Function [EB/OL]. Beijing: China Science Paper Online [2018-05-21]. http://www.paper.edu.cn/releasepaper/content/201805-178. (in Chinese)

[21] ALPARONE L. Multispectral and Panchromatic Data Fusion Assessment without Reference[J]. Photogrammetric Engineering & Remote Sensing, 2008, 74(2): 193-200.

Panchromatic and Hyperspectral Images Fusion Based on Non-negative Least Squares Algorithm

HAO Hongxun1HE Hongyan2,3ZHANG Bingxian2,3

（1 The Flight Technology College, Civil Aviation University of China, Tianjin 300300, China）（2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（3 Key Laboratory for Advanced Optical Remote Sensing Technology of Beijing, Beijing 100094, China）

The existing optical remote sensing image fusion methods focus on panchromatic and multispectral images. There will be the following problems while directly using these methods to deal with panchromatic and hyperspectral images. Due to the fact that hyperspectral bands are far more than multispectral bands, the existing methods are prone to grayscale distortion while synthesizing low-resolution panchromatic images by the weighted summation of hyperspectral bands. On the other hand, the existing optical remote sensing image fusion methods mainly use additive transformation, which can cause spectral or detail distortion in some ground objects because there are great spatial resolution difference between hyperspectral and panchromatic images. To solve the problems, this paper proposes the non-negative least squares algorithm based panchromatic and hyperspectral images fusion method. Firstly, this method reduces the bands of hyperspectral images by band compression. Then the low-resolution panchromatic images are generated by orthogonal least squares algorithm from the reduced bands and the panchromatic images. Finally, the fusion images are obtained by a ratio transformation model. The experiments demonstrated that the proposed method had a good performance on fusion quality, and was superior to the existed methods.

image fusion; hyperspectral image; non-negative least squares; remote sensing image; space remote sensing

TP79

A

1009-8518(2019)04-0105-07

10.3969/j.issn.1009-8518.2019.04.012

郝红勋，男，1977年生，2017年获中国矿业大学（北京）安全技术及工程专业工学博士学位，讲师。研究领域为航空航天新技术、飞行技术与航空安全、人机与环境工程。E-mail：hxhao8946 @aliyun.com。

2019-05-16

（编辑：王丽霞）