基于NPC的三相双有源桥式直流变换器的瞬时电流控制方法

王 宁,刘世林，鲁志远，赵传婷，周玉生

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

基于NPC的三相双有源桥式电路具有结构对称、控制简单、传输功率高、易于实现软开关等优点而被广泛应用于储能电池、直流输电、微网等领域。针对基于NPC的三相双有源桥式电路，传统的控制策略为单移相控制，该控制策略具有控制简单、易于实现等优点。但是，当单移相控制策略中输入/输出电压不匹配时，三相双有源桥式电路会出现部分开关管不能实现零电压开通，电流应力大等问题，因此,部分学者提出了三移相控制策略，即将两侧桥式电路中的占空比也作为控制变量。该控制策略可以增加控制维度，同一功率点对应的控制变量的组合有无数种，该控制策略往往使用一个或多个优化目标函数，对无数种控制变量组合进行寻优。事实上，当三相双有源桥式电路切换负载或引入其他扰动时，无论是三移相控制策略还是单移相控制策略，三相桥式电路中的电感电流均会发生三相不平衡以及直流偏置问题，影响变换器的暂态特性，严重情况下，可能会导致三相变压器磁饱和。

国内外学者针对双有源变换器出现的电感电流直流偏置问题做了大量研究，大体可以分为以下几种，第一种是使用非线性控制方法去解决此类问题，文献针对电感电流直流偏置问题，提出一种基于模型预测的最优轨迹控制，该控制方法需要通过高速电流传感器对电感电流进行检测，采集的电感电流作为最优轨迹控制的输入。这种控制方法可以有效抑制电感电流直流偏置问题，但是需要高速电流传感器增加了硬件成本。第二种是通过改变拓扑来减缓电感电流的直流偏置，文献在桥式电路交流输出环节添加了电容，利用电容“通交阻直”的特点减小变压器电流中的直流分量，这种控制方法需要在原有拓扑上添加新的硬件部分，增加了成本的同时又降低了原变换器的功率密度。第三种是通过对变换器的稳态及暂态进行建模分析，引入中间过渡状态的方式，比较典型的如文献通过引入中间变量的方法解决了单相双有源桥直流变换器中电感电流偏置问题，该控制策略不需要添加额外的传感器及其他硬件，降低了硬件成本，可以在一个开关周期之内有效地减小电感电流偏置。

以上的文献所研究的拓扑均是针对单相或三相两电平桥式拓扑，理论上来说对于两电平桥式拓扑所采用的电感电流优化策略均可以在基于NPC的三相双有源直流变换器上使用。但是基于NPC的三相双有源直流变换器在受到扰动时的暂态电流控制策略优化问题鲜有文章提及。基于此，研究针对基于NPC的三相双有源直流变换器提出一种可以优化三相暂态电流的控制策略，该控制策略同样不需要依赖传感器，且能在4/3个开关周期之内使系统达到稳定。

1 基于NPC的三相双有源桥式直流变换器拓扑及其控制策略

1.1 基于NPC的三相双有源桥式直流变换器拓扑

基于NPC的三相双有源桥式直流变换器拓扑如图1所示。两侧均由NPC三电平桥式电路组成，输入侧的电容为

C

；输出侧的电容为

C

；

R

代表负载。两个桥式电路由三相中频或高频变压器

T

连接，

L

，

L

，

L

表示变压器

T

的漏感及其线路的等效电感之和；同理

R

，

R

，

R

表示变压器

T

及其线路的等效电阻之和。和其他双有源直流拓扑一样，该拓扑具有结构对称，便于控制等优点。由于两侧桥式电路均采用全控开关管组成，因此能量可以双向流动，为便于分析，研究考虑的是能量从左侧向右侧流动。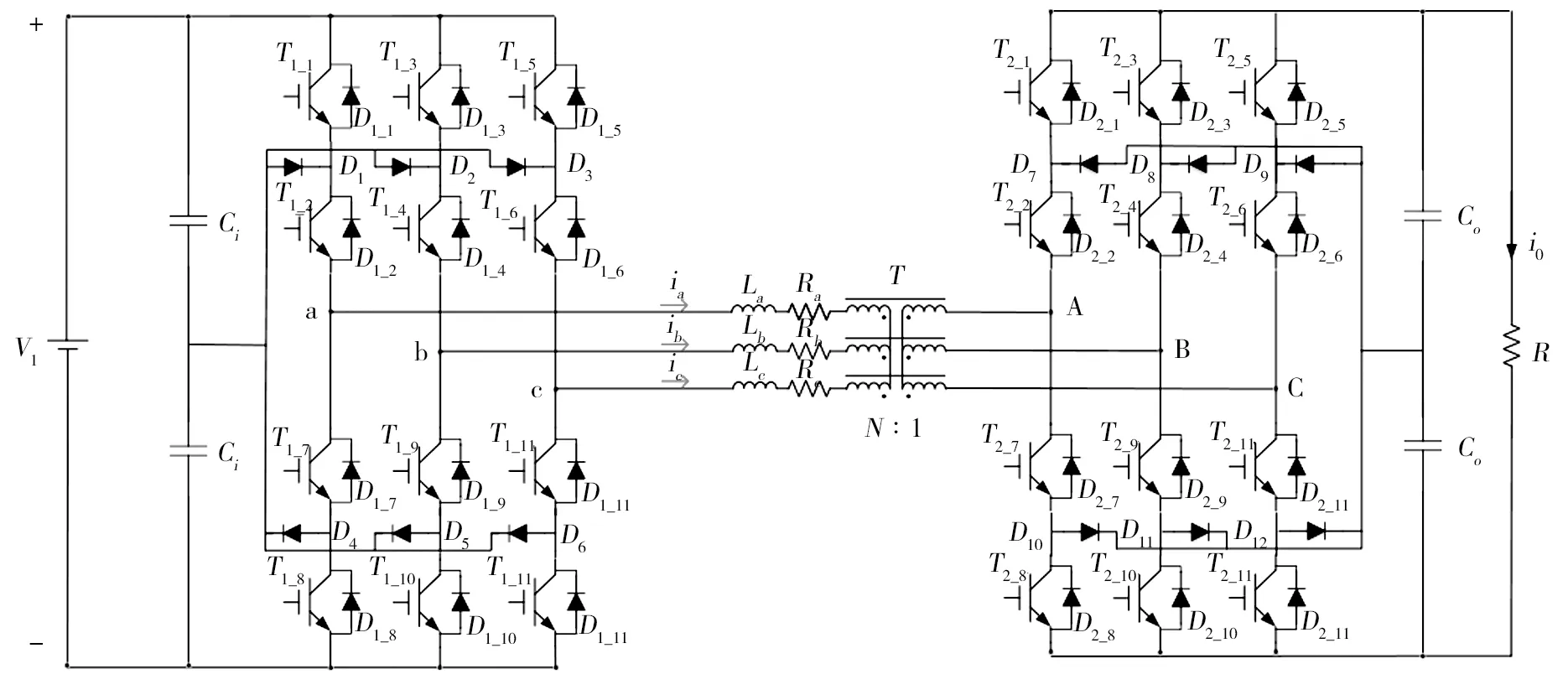

图1 基于NPC的三相双有源桥式直流变换器拓扑图

1.2 控制策略

基于NPC的三相双有源桥式电路具有结构对称、控制简单、易于实现软开关等优点，基于NPC的三相双有源桥式直流变换器如图2所示。由图2可知，

u

1，

u

1，

u

1分别表示左侧桥式电路中

a

，

b

，

c

三相桥臂中点电压波形；同理

u

2，

u

2，

u

2分别表示右侧桥式电路中

a

，

b

，

c

三相桥臂中点电压波形；

D

表示相电压波形中正电压或负电压占半个开关周期的占空比；同理，

D

表示相电压波形中正电压或负电压占半个开关周期的占空比；

D

表示左侧相电压波形中正电压中点到右侧相电压波形正电压中点的占空比。

图2 基于NPC的三相双有源桥式直流变换器

在传统移相控制策略中

D

与

D

均为1，即两侧桥式电路均输出相电压波形为100%占空比的方波，通过控制占空比

D

的大小和方向来控制桥式电路传输功率的大小和方向。由前文可知该控制策略不能实现所有开关管的零电压导通，因此，有学者提出三移相的优化控制策略，此时两侧桥臂电压的占空比不再是定值，而是一个可以变化的控制量，文中所研究的瞬时电流控制策略就是在三移相控制策略基础上提出来的。

2 瞬时电流控制策略

2.1 稳态分析

三相桥式电路正常工作下三相电流是完全对称的，以三相中的

a

相为例，左侧

a

相与右侧

a

相经变压器连接的等效电路如图3所示，

N

表示变比，是由等效串联电阻

R

及电感

L

和两个交流电压源组成的一阶微分电路。由叠加定理可知，图3可以分成两个新的支路如图4、图5所示。此时，两个支路分别仅包含一个独立电压源，独立电压源的大小仅取决于占空比的大小。以

a

相电路中左侧占空比

D

和支路1为例进行理论推导，得到的结论同样适用于右侧占空比

D

和支路2。由电感的特性方程可以得到：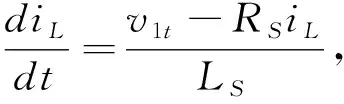

(1)

式中，

i

表示电感电流；

v

1表示等效电路中左侧激励源的瞬时值；

L

表示

a

相电感。由图2可知，假设系统已经达到稳态1，以中点电压波形

u

1的左侧边界为0时刻，稳态1的占空比为

D

。在稳态过程中，电感电流是以2

π

为周期的奇对称波形。由式(1)可以推导：

(2)

i

(

π

)=

I

+(

i

(0)-

I

)

λ

(

D

),

(3)

由于电感电流波形的奇对称特性，存在以下关系：

i

(0)=-

i

(

π

),

(4)

联立式(2)、式(3)，可以得到稳态时的电感电流在零时刻的值：

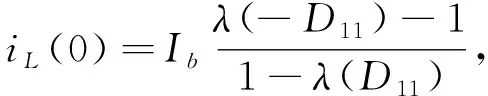
(5)

图3 等效电路图4 支路1

图5 支路2

2.2 暂态分析

传统控制策略如图6所示。由图6可见，假设直流变换器在零时刻发生扰动，一般情况下，对于传统的控制策略，占空比的指令会在零时刻立刻从

D

变为

D

。然而这种方法会导致电感电流产生直流偏置。在改进的暂态电流控制中，通过引入暂态占空比

D

11和

D

12，使电感电流的暂态过程限制在一个周期内，此后电感电流达到新的稳态，且占空比为

D

。经过前面的稳态分析，第二个稳态的零时刻电流为：

i

(

π

)=

I

+(

i

(0)-

I

)

λ

(

D

),

(6)

暂态过程中，电流满足以下的关系：

(7)

为了简化求解过程，取近似

λ

(

D

)=

e

/2≈1+

D

/2

f

π

。并将式(5)、式(6)、式(7)合并得到：

(8)

D

12=

D

-

D

-

D

11。

(9)

根据上述分析，对于

V

侧支路2同样可以得到：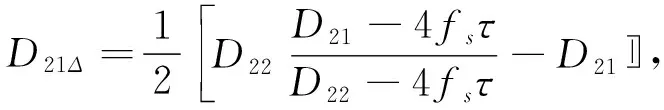

(10)

D

22=

D

-

D

-

D

21。

(11)

瞬时电流控制策略如图7所示。由图7可见，在分析暂态过程时，暂态电流控制策略通过引入暂态的占空比

D

11和

D

12使电感电流在发生变化时有一个过渡值，使电感电流在过渡区间后能够迅速达到稳态。考虑到基于NPC的双有源桥式直流变换器是三相对称系统，

b

，

c

相的理论分析与

a

相类似，因此在暂态中

b

，

c

相只需要添加和

a

相相对应的暂态变量，最终可以得到如图7所示的瞬时电流控制策略。

图6 传统控制策略 图7 瞬时电流控制策略

3 仿真验证

为验证研究所提的瞬时电流控制策略，在MATLAB/Simulink上建立仿真模型，具体仿真参数如表1所示，

V

侧直流电压值为100 V，输入电容

C

为5 000 uF；

V

侧直流电压值为60 V，输出电容

C

为500 uF。变换器的开关频率

f

为20 k，三相变压器的等效串联电阻

R

为0.2 ohm，三相变压器的漏感及等效串联电感之和

L

为35 uH。当三相双有源桥式直流变换器稳态运行时，研究使用的调制策略下有3个控制变量：

V

侧和

V

侧两个三相桥式电路的占空比分别为

D

和

D

，以及两侧三相桥式电路相应的开关函数基波之间的移相比

D

。变换器处于稳态1时的3个控制变量分别为：占空比

D

为0.259 8；

D

为0.388 5；移相角

D

为0.200 6。变换器处于稳态2时的3个控制变量分别为：占空比

D

为0.415 9；

D

为0.464 3；移相角

D

为0.200 6。在0.01 s，基于NPC的三相双有源桥式变换器由稳态1切换至稳态2，仿真结果如图8、图9所示。

表1 仿真参数

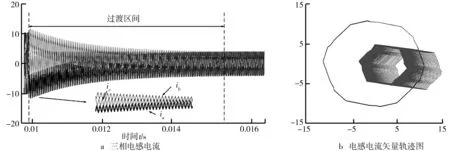
图8 传统控制策略下基于NPC的三相桥式变换器在受到扰动后的电感电流图以及电感电流矢量轨迹图

瞬时电流控制策略下基于NPC的三相桥式变换器在受到扰动后电感电流如图9a所示。由图9a可知，在0.01 s时功率指令发生变化，3个控制变量发生变化后，

a

，

b

，

c

三相电感电流无明显的偏置现象，降低了变压器造成磁饱和的风险；此外，在暂态过程中三相电流不对称度较小，且经4/3个开关周期的暂态就能达到新的稳态。此外，从图9b中的电感电流矢量轨迹图可以看到，经过4/3个开关周期，瞬时电流控制下的桥式变换器即可恢复至稳态。说明采用瞬时电流控制策略能够大大提高变换器的动态性能，仿真证明了所提策略的有效性。

图9 瞬时电流控制策略下基于NPC的三相桥式变换器在受到扰动后的电感电流图以及电感电流矢量轨迹图

4 结论

针对基于NPC的三相双有源桥式直流变换器提出了一种瞬时电流控制方法，当直流变换器的负载切换或受到其他扰动时，该控制方法在桥式直流变换器的两个稳态之间引入一个过渡区间，调节开关管的开关顺序以调节过渡区间内占空比大小，使得三相变压器三相电感电流仅经过4/3个开关周期的过渡区间就可达到平衡。通过分析三相双有源直流变换器的稳态特性和暂态特性，建立了三相双有源直流变换器在稳态和暂态过程的等效电路，最终得到三相桥式变换器在过渡区间内占空比的表达式。最后通过仿真验证该控制策略的有效性，该控制策略可以有效降低三相电感电流不平衡度以及电感电流直流偏置问题，防止变压器磁饱和，此外还能改善变换器的动态性能。