在概念的自主建构中深层理解意义

潘珍珍

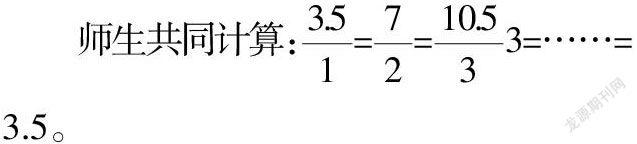
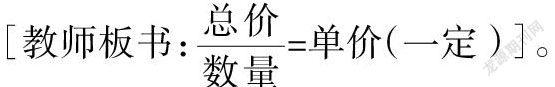
[摘  要] 数学教学是通过建构概念来引领学生跨进数学王国的大门的，但是由于概念比较抽象，小学生又以形象思维见长，因此，概念的建构与小学生的学习思维有所冲突。基于此，在教学中，教师可以通过初步探究，认识概念外延;探寻变化规律，揭示概念内涵;建构数学模型，凸显概念要素;借助数形结合，促进深层理解等环节来促进学生的学习，让学生自主建构概念，更加深入地理解概念的意义，学好数学知识。

[关键词] 正比例;概念;理解意义

数学教学是通过建构概念来引领学生跨进数学王国的大门的，但是由于概念比较抽象，小学生又以形象思维见长，概念的建构与小学生的学习思维有所冲突，因此数学概念的建构有赖于学生的感性认识，如何才能让小学生自主建构概念呢？笔者经过多年实践，发现只有引导学生聚焦概念特征，呈现出知识发生、发展的过程，才能使学生更好地自主建构概念，主动探究概念的深层意义，运用概念灵活解决实际问题。下面笔者以人教版六年级下册的“正比例意义”教学为例进行分析和探讨。

一、初步探究，认识概念外延

自主建构概念，就是要让学生自主地理解概念的外延和内涵。概念的外延是指此概念所适用的范围，概念的内涵是指此概念所反映事物的特有属性。建构“正比例关系”的概念时，凭借教材提供的有效材料，教师引领学生通过判断、思考，首先认识概念的外延。

[教学片段] （出示《卖彩带》场景图以及表格）

师：请同学们认真观察表格，说说表格中有哪两种量。

生：表格中有销售的数量和总价。

师：这两种量之间存在什么关系呢？

生：销售的数量发生变化时，总价就随之发生变化。

师：是的，总价随着销售数量的变化而变化，我们把这样的两种量叫作两种相关联的量。（板书：两种相关联的量）。

师：那总价是怎样随着数量的变化而变化的呢？

生：从左往右看，销售的数量增加，总价就随着增加;从右往左看，销售的数量减少，总价也就随着减少。

师：通过观察可以知道这两个相关联的量中，其中一种量变化，另一种量也会随着变化。在现实生活中，我们经常遇到两种相关联的量的变化情况，你还能举出一些这样的例子吗？

生1：正方形的边长越长，周长越大;正方形的边长越小，周长就越小。

生2：我们在排队的时候，排的排数越多，每排人数就越少;排的排数越少，每排人数就越多。

生3：我家离奶奶家近，我走到奶奶家所花的时间就短;我家离外婆家远，我走到外婆家所花的时间就长。

生4：我长大一岁，身高就会增长，体重也会增加。

这一教学环节中，教师通过实例让学生理清正比例关系的外延——“总价”与“数量”是两个相关联的量，并了解到两个相关联的量之间会存在着一些变化情况。“变化的量之间的关系”就是正比例关系概念的外延，学生厘清这个知识点以后就为建构正比例关系的概念扫清了障碍。

二、探寻变化规律，揭示概念内涵

在学生对“两个相关联的量”的特征有了正确的认识以后，教师要进一步引导学生探寻“总价为什么会随着销售數量的增加而增加”的变化规律，将学生的思维继续延伸下去，通过计算总价与数量的比值来观察算式，提炼出这两种量的共同变化规律，逐步揭示出正比例关系概念的内涵。

[教学片段]

师：请同学们再仔细观察表格，说说你还有什么新发现。

生：我发现彩带的单价没有变化。

师：真是个善于观察的孩子。彩带单价是怎么求到的？

生：总价除以数量等于单价。

师：“除以”我们可以用比的形式表示吗？

生：可以。

师：观察这条比例等式，你们发现了什么？

生：我发现这两种量的比值都是3.5，也就是相对应的两个量的比值不变。

师：这里的比值是3.5，实际上就是彩带的单价，这个单价一直保持不变。我们能不能把“不变”换成另外一个词来表示？

生1：可以换成“一定”。

师：（手指板书）总价和数量是两种相关联的量，总价变化，数量也随着变化，当总价和数量相对应的比的比值总是一定，也就是单价一定时，那我们就说总价和数量是成正比例的量，他们的关系叫正比例关系。

这一教学环节中，教师让学生分析具体事例，帮助学生建立一一对应的观念，让学生在交流中发现规律，计算比值后探寻出两个变量后面隐含着的不变量，从而明确了正比例关系的内涵特征——比值一定。从概念的外延推进到内涵的理解，帮助学生较快地掌握了正比例关系的含义。

三、建构数学模型，凸显概念要素

建构正比例关系的概念只凭一个例子，效果显然不会很明显。这时，教师还可以根据学生的学习情况，结合其他实例让学生辨别两个相关的量之间是否符合正比例关系，从而进一步明确正比例关系的判断要素，然后引导学生脱离情境，抽象概括出正比例的意义，建构数学模型，实现由具体数量关系到抽象模型的转化，这时就会有很明显的效果。

[教学片段]

师：刚才在学习两种相关联的量的时候，大家列举了一些生活中的事例，我们一起去看看这些关联的量是不是正比例关系。

生2：我们排队的时候，排数和每排人数不成正比例关系，因为每排人数×排数=总人数，这两个量之间不是除法的关系。

生4：我长大一岁与身高和体重不成正比例关系，因为我每年生长的高度都不同，体重增长也不同。

师：从你们所举的事例来看，判断两种相关联的量是不是成正比例，必须符合哪些条件？

生5：判断要素主要有三个——两个量是相关联的量，必须是变化方向一致，比值一定。

师：其中最主要的特征是哪一个？

生6：比值一定。

师：你能说说为什么吗？

生7：只要比值一定，其他两个条件也就符合要求。

师：如果用x和y表示两种相关联的量，用k表示它们的比值，正比例关系可以用怎样的式子表示？

这一教学环节中，教师让学生掌握了正比例关系中的“相关联的两个量”“变化”“比值”“一定”等要素的含义，并从中抽象出正比例数量的关系模型。这一教学过程，通过分析生活中常见的学习素材，把相关的知识纵向联系起来，对比思考其表征关系，从“变化”中发现了“不变”，让学生经历建构正比例关系概念的整个过程，概念的核心要素也就深深地留在学生的脑海中。

四、借助数形结合，促进深层理解

把抽象的数量关系与直观的几何图形相结合，这对于形象思维占优势的小学生来说无疑是一个最好的学习手段了。“数”与“形”合一，可以有效促进学生的学习思维从表层向深层跃进。

[教学片段] （多媒体出示彩带销售数量与总价的表格）

师：销售数量与总价这两个量，除了可以用表格表示以外，還可以用图象来表示。从图象中你读懂了什么？

生1：横轴表示数量，纵轴表示总价。

师：将表格中每两个相对应的量看作一个数对，如（1，3.5）对应的位置在哪里？你能将表格中的其他数对一一表示出来吗？

（请学生动手在书上画一画，再把这些点连起来，然后上台展示。）

师：这些点连起来成为什么？

生2：线段。

师：那要是把表格中省略号里表示的数对标出来，这条线段会向哪一端延伸？

生3：（0，0）是起点，只能向右上方无限延伸，这条线应该是射线。

师：正比例图象就是一条从（0，0）出发的无限延伸的射线。

师：纵轴上表示的总价和横轴上表示的数量是两种相关的量，那么总价是如何随着数量的变化而变化的呢？

生4：数量在增加，总价也在增加。

生5：这两个量变化的方向也是一致的。

师：再观察这条线上所有的点所对应的两个量，你有什么发现吗？

生6：我发现纵轴和横轴的两个量的比值都相等。

这一教学环节中，教师紧紧抓住正比例关系的本质特征，将表格转化为函数图像，把正比例中一一对应的函数思想直观建构在学生的脑海中，使原本抽象的数学知识变得直观形象、浅显易懂;学生“感性”地掌握了正比例关系的特征，对正比例关系概念的理解也变得更加丰满和深刻。

数学概念是学生学习数学知识的重要依托，让学生经历思辨过程，自主建构概念，有利于学生提高数学学习能力。教师在设计教学环节时，不仅要在揭示概念本质的特征上下功夫，还要高屋建瓴，从数学思想方面引领学生自主建构概念，促使学生更加深入地理解概念的意义，学好数学知识。

3387501908284