走向说理课堂

蔡美娜

[摘  要] 基于问题驱动的小学数学说理课堂力求在解决问题的过程中，既能促使学生对数学本质的理解，引领数学化和再创造，又能真正改变“教为中心”的课堂教学模式，让问题成为学生主动学习、深度说理的“驱动”。

[关键词] 问题驱动;说理;教学策略

当教育界的风向标聚焦“以学生为中心”时，课堂的生态发生了变化，从“基于教”到“基于学”，从“有意义”到“有意思”，从“不讲理”到“讲道理”，从“浅尝即止”到“深度说理”，从“关注知识”到“聚焦素养”，说理课堂的教学追求越来越明晰。构建“讲道理”的数学课堂，就要还数学以本来的面目，强调对数学本质的认识，让数学课堂成为师生共同成长的地方。在跟随罗鸣亮老师团队的实践中，笔者对基于问题驱动的小学数学说理课堂教学基本策略的脉络逐渐清晰，探索出了若干教学基本策略。

一、敢退能等，少教多学

在构建说理课堂的过程中，教师要注重学生的学习体验，要学会“退”，教师若没有“退”的意识，一切都无从谈起。在教学中教师只有适当“让位”，从课堂讲授转向组织学习，做到“少教”，才能释放时空，让学生真正成为课堂的主人。另外，教师要愿意等、能等、善等。“等”是一门学问，是尊重学生的表现，是让学习真正发生的需要。教师要充分认识学生的思维特点，不要一提问就马上想得到学生的回答，要善于“等待”。在一些思维的关键处，教师不仅要等待，还要引导优生也等一等，让其他同学有更充分的时间思考。另外，要放大“學”的过程。教师要以学生的学习为中心组织教学，给学生更多学的机会，通过设计丰富的学习活动，解决课堂上产生的问题，引导他们充分经历观察、操作、想象、描述、思考、交流、分析、推理等活动过程，实现每个学生的真正参与。

例1  “分饼——真分数与假分数” （北师大版五年级上册）教学片段

学生完成了自主学习，填写完了学习单后，交流汇报如下：

李婉秋：（展示自己的学习单并汇报）1. 真分数小于1;2. 假分数大于1，假分数可以变成带分数;3. 有一部分分数可以化成无限循环小数。

王磊：婉秋，你第二点有漏洞。如4/4是真分数还是假分数？

（婉秋回答不上来）

赖煜祺：我知道，4/4等于1，是假分数。

（婉秋在学习单上修正：假分数大于或等于1）

王希妍：我觉得第二点说“假分数可以变成带分数”不全面。像等于1，1就不是带分数。

（婉秋在学习单上第二次修正：假分数可以变成带分数或整数）

廖佳欣：（展示自己的学习单并补充）真分数<1，假分数≥1。

师：佳欣这样表述比文字更简洁。

马世成：（展示自己的学习单并补充）我认为，分子比分母小的分数叫真分数，例如：1/4，3/7……分子比分母大的或分子与分母相等的分数叫假分数，例如：4/4，6/5……

师：廖佳欣和马世成介绍了什么叫真分数，什么叫假分数，请大家再轻声读一读。

教师的“退”，促成了学生的“进”;教师的“隐”，凸显了学生的“显”。在这样的课堂上，师生之间、生生之间相互倾听、质疑与交流，真正实现了“少教多学”的说理课堂。

二、问题驱动，启发数学思考

1. “原生问题”驱动，开启思维之旅

“看到课题，你有什么想问的？”这可以成为说理课堂“概念课”的一种范式，如“什么是周长”“分数的认识”等数学概念课上，都可以引导学生看课题提问题。这样可以有效收集学生的问题，把握学习起点。

“认真阅读学习目标，思考我们今天要解决哪些问题？”在“复习课”上，可以让学生看学习目标提问题，把以陈述句表示的学习目标变成疑问句，以此激发学生的好奇心和探究欲，有利于梳理复习内容。

“你可以根据图中的信息提什么问题？”有趣好玩的情境总能引发学生的兴趣，“问题解决类（包括计算）”的课型可以让学生根据情境来提问题。

2. “核心问题”驱动，思考数学本质

教学内容的核心问题是由学科知识本身决定的，大多需要教师事先精心设计，教师适时地“进”非常必要，可以以一种善于预见的高度进行判断，开展有针对性的助学，把学生的思维引向深入。

例2  “确定位置”（北师大版四年级下册）教学片段

探究主题：利用列和行相结合的办法确定位置。

核心问题：如何确定你的好朋友的位置？

预设探究经过：

（1）经历“不能确定”。你更愿意选哪一个来猜？（我的好朋友在①北边;②旁边;③第二排;④第6排第2个）

（2）经历“能准确确定”。包括如何准确确定，如何用规范统一的办法来确定。

（3）经历“懂规范表达”。

（4）经历“会应用数对”。

3. “生成性问题”驱动，锤炼思维品质

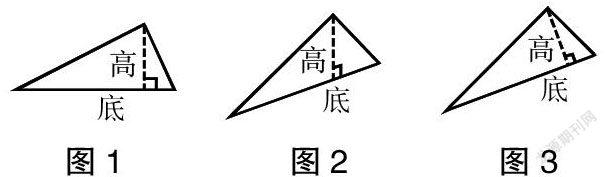
课堂是动态的，教师应关注教学的磕绊处，关注学生思维的困惑处，捕捉来自学生的生成性问题。如笔者在教学“三角形的认识”时，当一个三角形正着放（如图1）的时候，学生很容易画出它的高，但当三角形斜着放（图2）的时候，学生在画高时就很容易出错。当笔者把图2的正解（如图3）画在黑板上时，有学生轻声问道：“高怎么是斜着的？”经过追问，原来，该生认为生活中的高都是“竖着的”，比如量身高时，量房子的高时……这个问题的生成是受到生活经验的负迁移，是对概念本质理解的偏差，随后，“捕捉—放大—说理”，学生打乒乓球似的一来一回辨析“生活中的高与数学上的高”，从而认识了数学上的“高”，锤炼了数学思维品质。

三、关注探究，卷入式学习

问题是启学引思、导学引教的有效载体。课堂教学可以以一个个问题为学习支点，通过探究活动，驱动学生卷入式学习，在做中学，在学中思，经历数学创造过程的再现。苏霍姆林斯基说：“教育和教学的技巧和艺术在于，要使每一个儿童的力量和可能性发挥出来，使他享受到脑力劳动的乐趣。”笔者在多次公开课的课后调查中也发现，学生最喜欢的课堂活动都是自由探索，在做中学的环节。

探究活动可以设计成“学习任务”，通过小组合作，在解决学习任务的过程中令每一个学生都自然卷入。为了使探究学习不存在“无关人员”“游离人员”，教师可以根据探究任务灵活提出要求，如“独立思考后小組分享”“小组内确定发言代表随机抽”“小组分工式合作完成任务”等。这些必要的探究要求可以有效保证“不落下一个”，促使每个学生都主动思考、积极说理，使学习真正发生。

四、主动说理，建构深究型对话

“教育是能够导致学习的交流活动。”课堂上的互动不仅仅是教师与学生的互动，生生之间的互动应占据更大的份额，这样有利于建立反思性、循环性、相互依赖的互动方式。当然，教师也不能袖手旁观，该出手时要出手。

例3  “百分数的认识”（北师大版六年级上册）教学片段

生1：课本上说为了便于统计和比较，通常把18/20、8/10、21/25这些分数改写成分母是100的分数来表示，我还有一种方法，就是把不好比较的这几个分数改写成小数。小数和通分后的分数都挺容易比较的。

生2：既然小数和百分数比较起来都方便，为什么不改写为小数，而改写成百分数？

师：好问题！想要真正弄清楚一个问题，我们首先得弄清楚问题本身。大家可以商量一下什么是小数，再看一下课本，了解什么是百分数，弄清楚以后，再来思考这个问题。

（充分的交流和自学完成后）

生3：小数就是表示十分之几，百分之几，千分之几的数，百分数表示一个数是另一个数的百分之几，有点类似。

生4：小数表示一个数，而百分数表示一个数是另一个数的百分之几，也就是两个数之间的关系。

生5：看来小数和百分数都可以表示成分数，但是小数表示具体数量，百分数表示关系。

生6：这样好像就能说通了，分数不容易比较，小数虽然容易比较，但是不能表示两者之间的关系，所以产生了百分数。

至此，笔者再向学生展示5个分数、10个分数通分的过程，充分体会通分的麻烦，而且不仅仅是过程麻烦，即便是通分完毕，比较起来也很麻烦，进而明白百分数正是因为比较的需要才产生的。

在上述案例中，学生在得出不同解法时，自然产生了“既然小数和百分数比较起来都方便，为什么不改写为小数，而改写成百分数”的问题。教师不急于发表自己的意见，而是引导学生讨论，回到问题本身来思考什么是小数，什么是百分数，随后，“深究型对话”随即展开，生生互动，思维碰撞，回到概念的意义来思考问题，学生获得了深刻的理解。

综上，基于问题驱动的小学数学说理课堂力求在解决问题的过程中，既能促使学生对数学本质的理解，引领数学化和再创造，又能真正改变“教为中心”的课堂教学模式，让问题成为学生主动学习、深度说理的“驱动”。

3387501908216