Fischer-Tropsch合成油正构烷烃尿素络合物非等温热分解动力学

于婉秋，韩冬云，石薇薇，乔海燕，曹祖宾，朱衣点

（1. 辽宁石油化工大学 石油化工学院，辽宁 抚顺 113001；2. 江苏斯尔邦石化有限公司，江苏 连云港 222000）

Fischer-Tropsch合成是煤制油工艺的核心技术，主要过程是将合成气经催化反应转化为液态烃，经深加工实现油品的增值利用，所得的低温Fischer-Tropsch合成轻质馏分油（F-TLD）产品具有正构烷烃含量高，烯烃组分多为α-烯烃，硫含量低、几乎不含芳烃等特点，可继续加工生产高附加值的化工产品，如液体石蜡等［1-4］。液体石蜡是重要的有机化工原料，可以生产如α-烯烃、氯化石蜡和高级脂肪醇等一系列化工产品。因此，从Fischer-Tropsch合成油品中分离正构烷烃具有重大意义。正构烷烃的分离方法主要有尿素脱蜡（络合）法和分子筛脱蜡法。与分子筛脱蜡法相比，尿素络合法无论在投资、产品品种、质量、价格还是装置灵活性均占有一定优势［5-6］。在尿素络合正构烷烃的过程中，随着反应体系温度的降低，尿素与溶液中的正构烷烃络合后由正方晶体转变成内含正构烷烃的六棱柱络合物结晶。而尿素络合物（UIC）不够稳定，温度对它影响较大，若能适当调节络合温度，则可大大提高正构烷烃的分离效果。因此，对UIC的热分解机理进行深入研究具有重大意义［7-12］。在UIC的非等温热分解动力学研究中大多数集中于以纯物质为客体的UIC，对混合油品尤其是Fischer-Tropsch合成油的热分解机理研究甚少。为提高Fischer-Tropsch合成油品中正构烷烃的分离效果，需找到混合油品中正构烷烃UIC的非等温热分解机理。

本工作以F-TLD为原料，正壬烷（C9）和正十二烷（C12）为参照，采用尿素络合法分离油品中的正构烷烃，对中间产物UIC的热分解行为、动力学规律及热分解机理进行研究。通过考察UIC的TG-DTG曲线而研究其热分解过程，根据Coats-Redfern法和Doyle法求出热分解反应的动力学参数和热力学参数，推导出可能的分解反应机理及反应动力学方程和动力学补偿表达式。

1 实验部分

1.1 试剂与原料

尿素、异丙醇、石油醚、C9、C12：分析纯，上海阿拉丁生化科技股份有限公司。原料油为内蒙古伊泰煤制油公司生产的Fischer-Tropsch合成油精馏切割130～220 ℃馏分，组分主要为正构烷烃和异构烷烃，碳数主要分布在9～12之间，其中正构烷烃含量48.8%（w），异构烷烃含量51.0%（w），其他组分含量较少（0.2%（w））。在络合过程中，尿素主要与正构烷烃进行络合反应，从而实现正构烷烃的分离。因此，油品中其他组分对于UIC非等温热分解动力学的研究不产生影响。

1.2 UIC的制备

将尿素、异丙醇和水按照一定比例配制成络合溶液，与原料油一并加入到络合反应器中进行络合反应。在不断搅拌的条件下，络合物逐渐聚集，形成固体颗粒后悬浮在体系中。待反应结束后停止搅拌，进行固液分离，得到固相络合物和滤液。以石油醚为溶剂对固相络合物进行洗涤，除去附着在络合物上未反应的油。将UIC加热分解，释放被络合的正构烷烃，经水洗、蒸馏等处理获得富正构烷烃的粗蜡液产品。将滤液相同样经水洗、蒸馏等处理获得富异构烷烃的脱蜡油。

将上述石油醚洗涤后的固相络合物进行干燥，取样作为进一步研究的原料。

1.3 尿素络合物的表征

采用安捷伦科技有限公司FTIR-660+610型红外显微光谱仪对UIC结构进行FTIR表征，KBr压片，光谱分辨率优于2 cm-1，波数精度0.05 cm-1，波数重现性0.005 cm-1，测量范围400～4 000 cm-1；采用美国TA公司Q600型热重-差热分析仪对UIC进行TG-DTG表征，氮气氛围下，以空坩埚为参比物，装载量为2～5 mg，以5 ℃/min的速率由室温升至260 ℃，通过电脑软件获得TG-DTG曲线。

2 结果与讨论

2.1 UIC结构的FTIR表征结果

图 1为 三 种 UIC（C9-UIC，F-TLD-UIC，C12-UIC）与尿素晶体进行对比的FTIR谱图。由图1可知，三条曲线形状相近，这是由于络合在尿素孔道中的客体相同，主要为正构烷烃。尿素在3 445，3 348 cm-1处有N—H键的对称伸缩振动和反对称伸缩振动的吸收峰，在1 679，1 626 cm-1处有C=O键的伸缩振动吸收峰，两个肩峰的形成是由羰基的振动耦合所致，在1 457 cm-1处有C—N键的伸缩振动吸收峰，在1 160 cm-1处有—NH2的面内摇摆振动吸收峰，而587 cm-1处有尿素骨架N—C=O的伸缩振动吸收峰；C9-UIC，F-TLD-UIC，C12-UIC的N—H键的对称伸缩振动吸收峰分别移至3 447，3 415，3 421 cm-1处，反伸缩振动吸收峰分别移至3 261，3 224，3 226 cm-1处，并且在N—H键的对称伸缩振动及反对称伸缩振动处的吸收峰变宽，说明络合后尿素分子间形成氢键，形成了尿素六角形三维通道。三种UIC在2 960，2 870 cm-1处的—CH3反对称及对称伸缩振动特征吸收峰向低波数段移动，这可能是因为客体在UIC中有一些振动是受限制的而在纯客体时是较为自由的［13］，证明三种体系中尿素均成功络合正构烷烃。1 679 cm-1左右的C=O伸缩振动特征吸收峰减弱，尿素骨架的N—C=O伸缩振动吸收峰移至608 cm-1左右，这正是六方UIC中空管道的N—C=O伸缩振动特征吸收峰，再次印证三种体系中均形成了UIC。

2.2 UIC的TG-DTG表征结果

图2为UIC的TG-DTG曲线。由图2可知，络合物的热分解过程分3阶段：1）体系在50～125 ℃之间失重，C9-UIC，F-TLD-UIC，C12-UIC的失重率分别为1.24%，8.88%，17.55%，为六方UIC的热分解，释放客体分子并形成四方尿素分子，体系逐渐由固相变为液相；2）体系在125～220 ℃之间失重，根据尿素的熔融温度可知，该处失重为尿素熔融并热分解导致；3）体系在220～250 ℃之间失重，根据被络合油品的馏分可知，正构烷烃分子汽化逸出，体系达到恒重，热分解完成。由图2还可知，UIC固相热分解过程为1）阶段，因此选取此阶段进行热分解动力学研究。

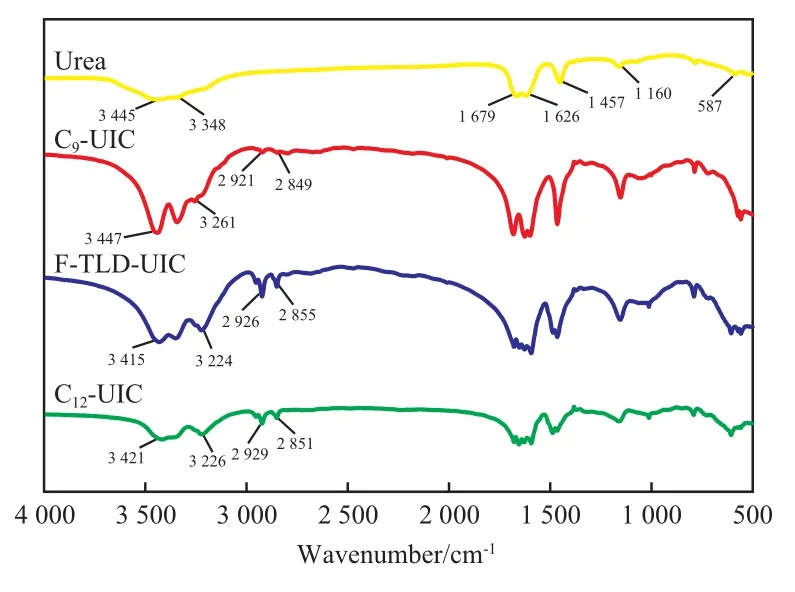
图1 三种UIC（C9-UIC，F-TLD-UIC，C12-UIC）与尿素晶体进行对比的FTIR谱图Fig.1 FTIR spectra of three urea inclusion compounds(UIC)

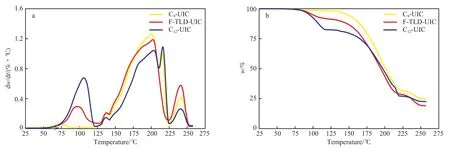
图2 UIC的TG-DTG曲线Fig.2 TG-DTG curves of UIC.

2.3 UIC固相热分解动力学研究

F-TLD-UIC固相热分解过程的微分和积分形式动力学方程分别见式（1）和式（2）。

式中，α为t时刻物质A已反应的分数；t为时间，min；k为反应速率常数；f（α）为微分形式的动力学机理函数；G（α）为积分形式的动力学机理函数。f（α）与G（α）之间的关系见式（3）。

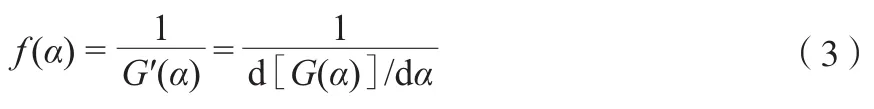
k与反应温度之间的关系可用Arrhenius方程式（4）求得。

式中，A为表观指前因子，s-1；E为表观活化能，kJ/mol；R为摩尔气体常量，J/（mol·K）；T为反应温度，K。

F-TLD-UIC固相热分解过程为非等温过程，则有式（5）存在。

式中，T0为TG曲线偏离基线的始点温度，K；β为恒定加热速率，K/min。

由方程式（1），（4），（5）可得微分式（6）和积分式（7）。

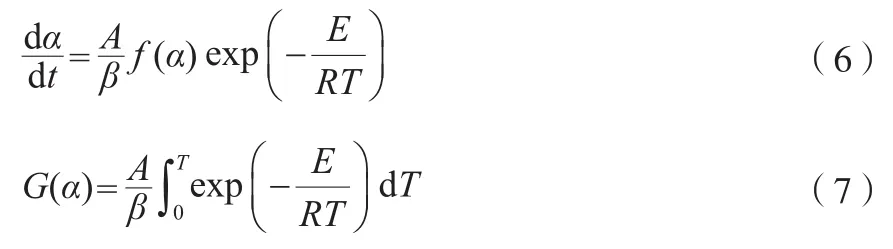
2.3.1 Coats-Redfern法

采用Coats-Redfern法［14］求取动力学参数。图3为C9-UIC，F-TLD-UIC，C12-UIC的lnln［1/（1-α）］与1/T的拟合曲线。

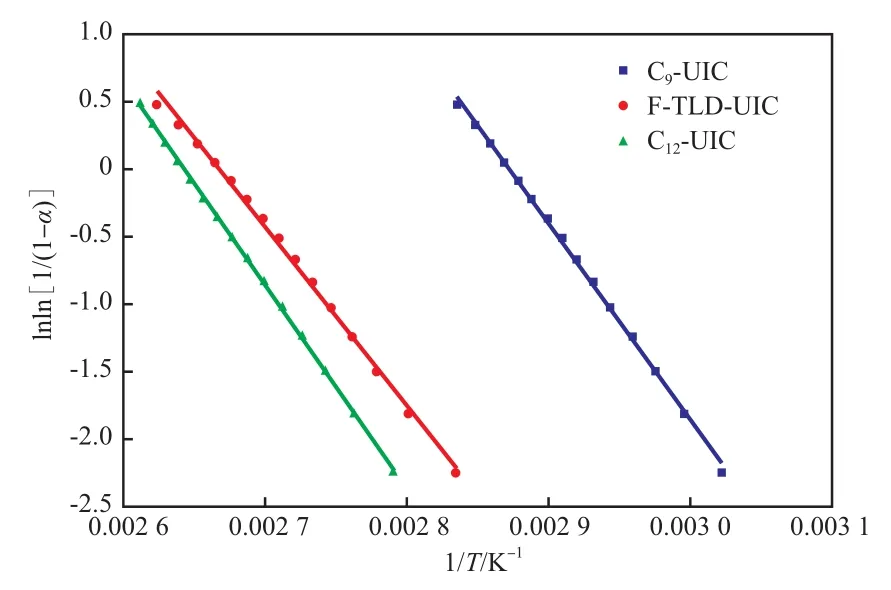
图3 C9-UIC，F-TLD-UIC，C12-UIC的lnln［1/（1-α）］与1/T的关系Fig.3 The relationship between lnln［1/(1-α)］and 1/T of C9-UIC，F-TLD-UIC，C12-UIC in thermal decomposition process.

经计算，三种UIC拟合曲线的方差分别为0.998 6，0.996 6，0.999 7，均符合良好的线性关系，表明UIC的热分解为一级反应（n=1），即f（α）=1-α，G（α）=-ln（1-α）。则 Coats-Redfern方程可选用式（8）。

式（8）中2RT/E项若随温度变化很小，在程序升温过程中可视为常数，故ln［G（α）/T2］对1/T做图应是一条直线，从斜率可求得E，取反应过程的平均温度，从截距中求得A。取16种常见固体热分解反应机理分别代入式（8），用最小二乘法求得线性相关系数（R2）。

2.3.2 Doyle法

采用Doyle法［14］求取动力学参数，见式（9）。

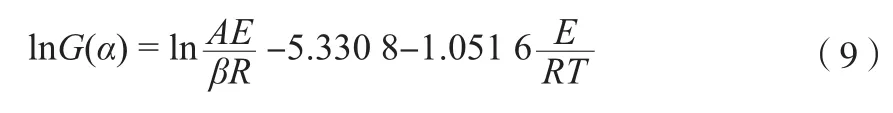
由式（9）可知，lnG（α）与1/T为线性关系。同理，取16种常见固体热分解反应机理分别代入式（9），用最小二乘法求得R2。同时，从直线的斜率中求得E；从截距中求得A。

2.3.3 热分解动力学的确定

采用Coats-Redfern法和Doyle法对三种络合物的热分解动力学过程进行分析，将α-T的实验数据分别代入式（8）和式（9）中进行参数计算，结果见表1和表2。两种计算方法的结果比较接近，但由于应用Doyle方程的条件比Coats-Redfern方法更严格，Doyle法拟合的相关性较Coats-Redfern法普遍有所提高。判断固相分解反应机理时，一般是以相关性作为主要判据，如相关性均较为合适时，可选取残差平方和（SSE）作为辅助判断以确定最佳的分解反应机理。由表1和表2可知，扩散机理、相界面反应机理及成核和核成长控制（A1）机理的R2均大于0.99，特别是Avrami-Erofeev的随机成核和随后生长机理的相关性最好，其中尤以A1机理的相关性最好。因此，从考虑R2和SSE这二方面出发，络合物热分解反应取A1机理比较合理。

按相关性较好的Doyle方程来求取动力学参数，计算C9-UIC，F-TLD-UIC，C12-UIC在氮气中的热分解活化能分别为115.28，104.56，118.97 kJ/mol，表观指前因子分别为1.91×1015，2.86×1012，2.23×1014s-1。求得的热分解活化能在热分解温度范围内均满足Doyle方程的20≤E/RT≤60这一假设，说明采用Doyle方程是合理的，故F-TLD-UIC相应的动力学方程式为：

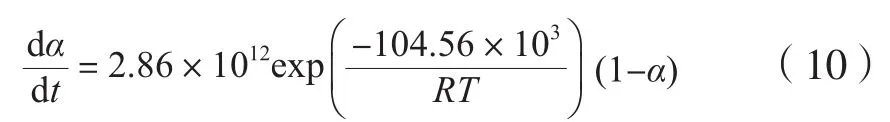
为了进一步确定A1反应机理的合理性，对由TG实验确定的反应速率dα/dt（等面积图解微分法求得）与按式（10）模型计算的结果进行了对比，结果见图4。由图4可知，实验点和模型点吻合情况较好，从而证明了此反应机理模型的合理性。

根据动力学补偿效应表达式：lnA=aE+b，式中，a，b为补偿参数，利用表2中的数据，对lnA～E进行线性拟合，求得三种络合物的补偿参数及动力学补偿表达式见表3。由表3可知，F-TLD-UIC动力学补偿表达式为lnA= 0.31E-4.45。

求得E和A后，热力学参数热分解过程的焓变ΔH、熵变ΔS及摩尔自由能变ΔG即可计算得到。三种UIC的主要热力学参数汇总见表4。

表1 采用Coats-Redfern法对UIC热分解反应的各种固相反应机理的拟合结果Table 1 Fitting results of various solid-phase reaction mechanisms of thermal decomposition reaction of UIC by Coats-Redfern method

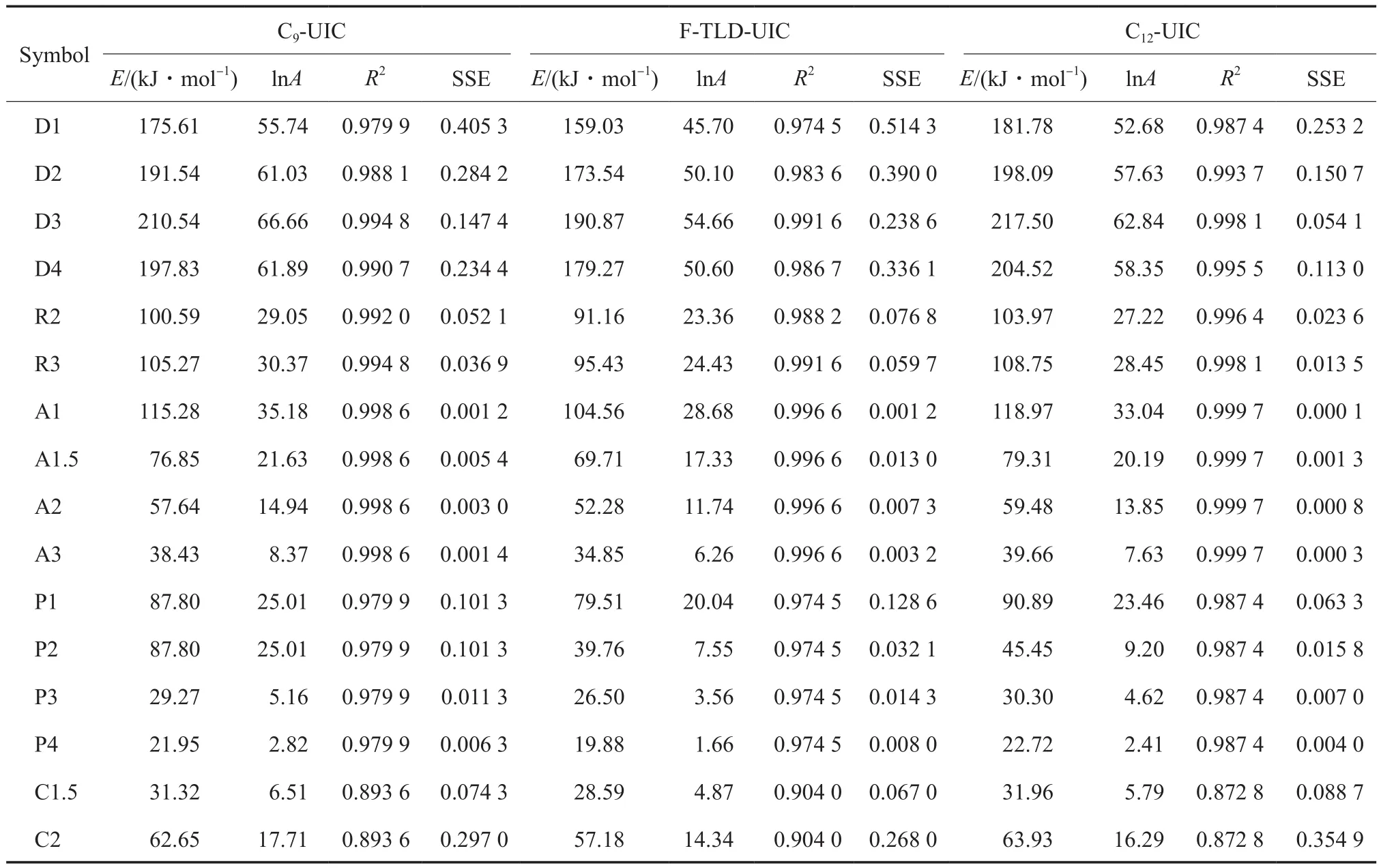
表2 采用Doyle法对UIC热分解反应的各种固相反应机理的拟合结果Table 2 Fitting results of various solid-phase reaction mechanisms of thermal decomposition reaction of UIC by Doyle method

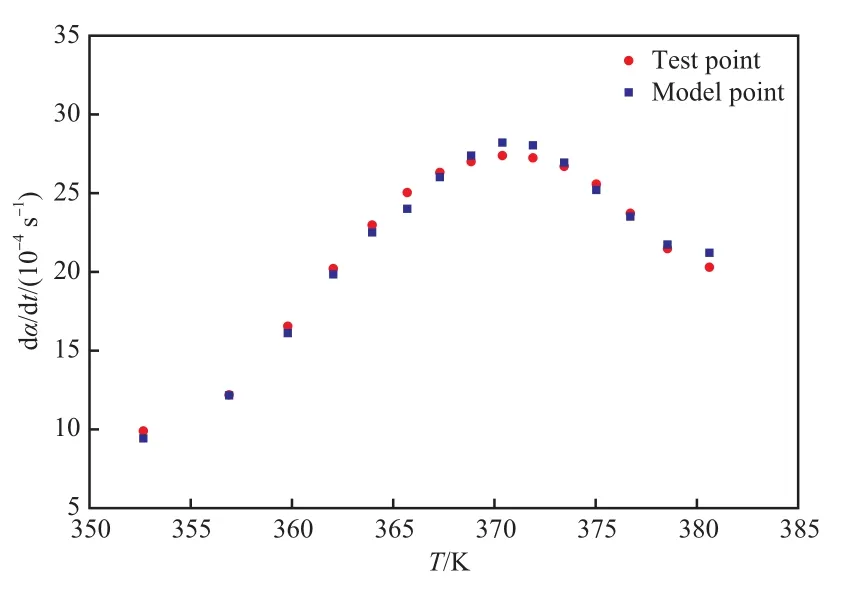
图4 dα/dt的实验点与式（10）计算点对比Fig.4 Comparison between the test value of dα/dt and the model value of equation (10).

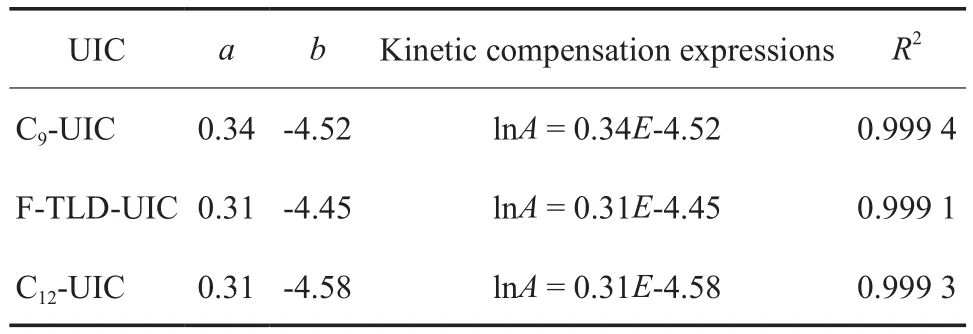
表3 UIC热分解动力学补偿参数及表达式Table 3 Kinetic compensation parameters and expressions for thermal decomposition of UIC

由表4可知，F-TLD-UIC热分解过程的ΔH=101.50 kJ/mol，ΔS= -73.95 J/（mol·K），ΔG=128.75 kJ/mol。

表4 UIC的热力学参数Table 4 Thermodynamic parameters of UIC

3 结论

1）F-TLD-UIC，C9-UIC，C12-UIC的热分解动力学研究结果具有一致性；UIC在氮气氛围中的热分解反应为一级反应，属于Avrami-Erofeev的随机成核和随后生长机理为控制步骤的A1机理。

2）采用Coats-Redfern法和Doyle法对UIC热分解动力学过程进行分析发现，Doyle方程的条件比Coats-Redfern法的更严格，拟合的相关性较Coats-Redfern法普遍有所提高。

3）按Doyle方程求解三种UIC热分解动力学参数得：F-TLD-UIC，C9-UIC，C12-UIC热分解活化能分别为104.56，115.28，118.97 kJ/mol，表观指前因子分别为2.86×1012，1.91×1015，2.23×1014s-1；F-TLD-UIC的非等温热分解动力学方程为dα/dt=2.86×1012exp（-104.56/RT）（1-α）；动力学补偿表达式为lnA= 0.31E-4.45；热分解过程的ΔH=101.50 kJ/mol，ΔS= -73.95 J/（mol·K），ΔG=128.75 kJ/mol。