基于声发射监测的不同加卸荷路径下砂岩破坏前兆信息研究

徐 婕，徐 宁，蒋景东

(1.河海大学 岩土力学与堤坝工程教育部重点实验室， 江苏 南京 210098；2.青岛市莱西水利局， 山东 青岛 266600； 3.南京水利科学研究院， 江苏 南京 210024)

岩石材料性质、应力路径和围岩条件复杂多样，制约了岩体破坏先兆信息研究。岩石的变形和破坏是一个内部微观裂隙萌生、扩展和交汇的过程。在这个过程中，岩石内部的弹性应变能以弹性波的形式不断地释放，这就是所谓的声发射(AE)[1-5]。通过研究岩石破裂演化过程中声发射信号的变化规律，来揭示其破裂演机制，并探讨其破裂前兆[6-9]。Chmel等[10]开展了一系列花岗岩压缩条件下动态破裂过程的声发射特性的试验研究，这有助于评估非平衡条件下声发射事件间的相互关系。基于双轴压缩试验，Baddari等[11]采用电磁辐射和声发射对大型岩石试样的破坏过程进行研究，相关成果为岩石动态失稳破坏提供了一个分析平台。Thompson等[12]开展了花岗岩三轴压缩试验，根据声发射监测结果，发现了裂隙破裂演化成核的新规律。此外，研究结果表明，完整岩石的破裂成核和黏着滑动测试的动态失稳破裂成核具有相似性。张晖辉等[13]开展三轴循环荷载试验对片麻岩的破坏前兆进行声发射研究，结果表明声发射信号参量在时间域和空间域的分布上都具有分形特征。马胜利等[14]在对不同断层类型破坏的声发射特征进行了研究，结果发现对于非连续断层临界滑动失稳前，声发射活动出现了明显的平静现象。现有的研究多集中在探讨单一应力路径下岩石应力、应变和声发射参数的关系，比如受拉、受压和剪切。相比之下，对于复杂应力路径下声发射活动的理论和试验研究比较少。本文针对砂岩进行了一系列不同应力路径下的加卸荷试验研究，并采用极点对称模态分解方法对声发射信号中的噪音信号进行处理，在此基础上对不同应力路径下的声发射数据进行了分析。基于分形理论，定量分析了卸荷路径对声发射特性的影响，以此来探测岩石的破坏前兆，相关研究为评价和预防岩石的应力诱发失稳问题提供了理论依据。

1 试验方案

1.1 试样制备

本文试验中采用的砂岩取自安徽淮南煤矿，X射线衍射(XRD)结果表明，该砂岩的矿物成分为石英石12.1%、钾长石10.9%，斜长石38.7%，方解石13.4%，白云石12.7%，赤铁矿2.8%，黏土矿物9.4%。砂岩的孔隙率和密度分别是7.02%和2 613 kg/m3，所有的砂岩均从同一块材料取芯，然后被制作成直径和高度分别是50 mm和100 mm的标准圆柱样品，如图1所示。

图1 砂岩标准圆柱试样

1.2 试验设备

所有的试验都是通过MTS815伺服控制岩石力学试验机开展的，整个试验过程是由计算机控制的，实现了数据的自动采集和处理。试验过程中的声发射是采用16通道的PCI-II系统进行监测，增益和门槛值设为55 dB以提高信噪比。为了保证三维定位的准确性，6个声发射探头设置在三轴压力舱外作为一个传感器矩阵，其中探头的类型是Nano30,相应的工作频率是100 kHz～400 kHz。为了确保声发射探头与试样的耦合效果，在试验开始前要进行断铅试验。

1.3 试验方法

不同应力路径下的试验方案设置如下：

(1) 常规三轴加载试验(方案Ⅰ)。常规三轴加载试验分别在10 MPa、20 MPa、40 MPa、50 MPa不同的围压条件下进行。首先，围压以0.1 MPa/s的速率加载到设计值，使试样处于静水压力状态。之后保持围压不变，以恒定的轴向位移率0.001 mm/s进行轴向加载直到试样破坏，以保证获得完整的应力应变曲线。通过常规三轴加载试验获得的峰值强度可以为卸围压试验的卸荷点的确定提供依据。

(2) 增轴压卸围压试验(方案Ⅱ)。首先，将围压加载到设计值(10 MPa、20 MPa、40 MPa和50 MPa)。随后围压保持不变，轴压加载到常规三轴试验峰值强度的80%，然后以0.3 MPa/s的恒定速率加载轴向应力，同时以0.5 MPa/s的恒定速率卸载围压，直至试样破坏。

(3) 恒轴压卸围压试验(方案Ⅲ)。首先将围压加载到设计值(10 MPa、20 MPa、40 MPa、50 MPa)。其次，围压不变，轴向应力加载到常规三轴试验峰值强度的80%。保持轴向应力不变的同时，围压以0.5 MPa/s的恒定速率卸载，直至试样破坏。

2 极点对称模态分解方法

声发射信号在采集的过程中不可避免会混入外在噪音，噪音信号的处理效果直接影响数据分析的准确性。本文采用“极点对称模态分解方法”对声发射信号中的噪音信号进行处理。

极点对称模态分解方法是利用“最小二乘法”优化“剩余模态”，以此来定义“自适应全局均线”，由此分析“最佳筛选次数”。这种方法确定的“剩余模态”可自动搜索最佳极值点个数，且能保证“自适应均线”是最优性，以此来避免人为定义的误差。其模态分解方程为[15]：

(1)

式中：s(t)为原始数据信息；ci(t)为原始数据分解后的频率模态；n为分解的不同频率模态个数;R(t)为最优分解后的剩余模态。

3 试验结果

3.1 加载条件下砂岩的声发射特征

图2给出了方案Ⅰ在不同围压条件下砂岩破坏过程中轴向应力差和振铃计数率随时间的变化曲线。在加载早期，声发射活动较为活跃，这主要来源于初始裂隙和孔洞的闭合。进入塑性阶段后，振铃计数率逐渐增加，说明试样中开始出现新的裂纹。当试样到达膨胀应力后因为膨胀效应出现了体积膨胀，此时声发射信号明显增强。当试样内部出现较大裂纹时，裂纹尖端产生应力重分布，并伴随着能量耗散。在这个过程中，能量释放率逐渐降低，声发射参数比如振铃计数率降低，这就是声发射平静期[16-17]。如图2所示，随着围压的增加声发射平静期逐渐变得明显，主要是因为高围压限制下新生裂纹的数量相对较少。当围压从10 MPa增加到50 MPa时，声发射平静期从20 s持续到57 s，裂隙扩展过程由裂隙萌生向裂隙聚集交汇过渡。

不同围压作用下砂岩试样变形过程中的应力和声发射特征表现为:

(1) 常规三轴压缩试样主要以剪切破坏为主，其残余强度较高。

图2 方案I不同围压条件下砂岩破坏过程的轴向应力差和计数率随时间的变化曲线

(2) 当围压较高时，峰值后应力无显著跌落，残余强度随围压不断增大，原因在于较高围压会对试样产生更大的限制作用。

(3) 整个过程都会持续释放声发射信号，且信号整体较强。

(4) 峰值点的振铃计数率随着围压不断增大，监测数据显示振铃计数率从59 次/s增加到145 次/s，说明较高围压会导致试样在加载的过程中积聚更多的能量，破坏时也相应地释放更多能量。

(5) 最大的振铃计数率出现在峰值之后，而不是峰值位置，并随着围压的增大而增大。原因在于试样在围压的束缚下仍然具有一定的承载力，破裂的试样块体一般只有当应力跌落至残余应力才会发生较大的滑移。

在常规三轴压缩条件下，平静期可以作为试样破坏的前兆信息。围压改变了试样的应力状态，延长了裂纹扩展过程，延迟了断裂的发生，增加了声发射振铃计数率。

3.2 卸荷条件下砂岩的声发射特征

图3为方案Ⅱ不同围压条件下砂岩破坏过程的轴向应力差和计数率随时间的变化曲线。方案Ⅱ中，在卸载点之前，振铃计数率逐渐增大，如图3(a)所示。结果表明，应力-应变曲线在卸载点处存在明显的拐点，计数率突然增大。卸荷点10 s后砂岩试样突然破坏，计数率在74.9 s时达到最大值131次/s。可以看出，围压从10 MPa增加到50 MPa时，峰值的计数率从131 次/s增加到296 次/s，说明随着围压的增加，试样的破坏更加剧烈。如图3(b)所示，计数率-时间曲线在卸载前出现了30 s的平静期，以此作为样品失效的前兆信息是不合适的，因为此时样品内部没有产生新的裂纹。当试样开始卸载时，计数率突然增加，说明试样中出现了新的裂纹。随着卸载的进行，计数率不断增加，直至峰值轴向应力差达到148.03 MPa。方案III的计数率与方案Ⅱ有相同的变化规律。与方案Ⅰ不同，方案Ⅱ和方案Ⅲ在失败前没有明显的前兆特征，在试样破坏时计数率最大。

图3 方案Ⅱ不同围压条件下砂岩破坏过程的轴向应力差和计数率随时间的变化曲线

3.3 不同加卸荷条件下砂岩破坏的声发射前兆

为了进一步研究不同应力路径下砂岩试样的破裂演化特征，需要抓住声发射信号的分析特征对其进行量化分析。在延迟坐标状态空间重构法中，假定延迟坐标的维数m与序列维数d的关系是m≥2d+1，计算过程基于G-P算法：将试验过程中单个岩样的声发射强度作为容量为n的序列集：

X={x1，x2,…，xn}

(2)

取序列中并列的m个数作为m维空间的第一个向量，

Y1={x1，x2,…，xm}

(3)

依次再取m个数构成第二个向量，

Y2={x2，x3,…，xm+1}

(4)

构成N=n-m+1个向量，根据Takens原理，空间中两点间距离小于r的概率的累积分布函数W(r)：

(5)

式中，u为Heaviside函数，

(6)

而|Yi-Yj|为空间相点Yi与Yj间的距离,r为量测尺度，通过对数据点(lgW(r),lgr)直线拟合，得到斜率D(m)即为声发射的分形特征：

D(m)=lgW(r)/lgr

(7)

3.4 分形维数随应力比的变化

图4给出了不同应力比下砂岩试样的声发射分形值，应力比为轴向应力差与峰值应力差之比，分形值曲线如图4(a)和图4(b)所示，当应力比为0.2～0.4时，砂岩试样处于由初始压缩向弹性变形的过渡阶段。在围压的影响下，分形值的增长速度较慢，甚至出现下降。当应力比为0.4～0.8时，常规三轴加载试验分形值先增后减，原因在于围压的约束使得裂纹扩展缓慢。卸载条件下的试样裂纹扩展很快，分形值先减后增。当应力比为0.8～1.0时，试样的应力接近峰值，试样中的裂纹扩展汇合成剪切破裂带[18-19]。剪切带的形成导致了试样的脆性破坏，不同应力路径下的分形值迅速减小。这一阶段的声发射可以用来研究试样在不同应力路径下的破坏前兆。方案II分形值下降速率最高，方案III分形值下降速率次之。方案I的递减率最低。

随着围压的增大，如图4(c)和图4(d)所示，砂岩试样分形值呈现不同的变化趋势。当应力比在0.4～0.8范围内时，高围压使得砂岩试样中裂纹的萌生、扩展和合并速度减慢。卸载条件下试样分形值的变化趋势与常规三轴加载条件相似，即先上升后下降。当应力比为0.8～1.0时，不同应力比下声发射特征的差异减小，试样破坏前分形值的减小规律也发生改变，原因在于增大的围压产生了更大的约束作用。

图4 砂岩试样在不同应力路径下声发射的分形值 (应力比)

3.5 分形维数随时间比的变化

将时间比定义为加载时间和破坏时间之比，则时间比的最大值为1。图5给出了不同时间比下砂岩试样声发射的分形值曲线。由图5(a)和图5(b)可知，当时间比为0.4～0.8时，不同应力路径下试样的分形值先减小后增大。当时间比大于0.8时，声发射特征变化趋势不明显。如图5(c)和图5(d)所示，方案Ⅰ砂岩试样在不同时间比下的分形值变化不大。当时间比大于0.8时，卸荷路径下砂岩试样的分形值迅速减小，这可以作为高围压下岩石破坏的先兆预测[20-21]。

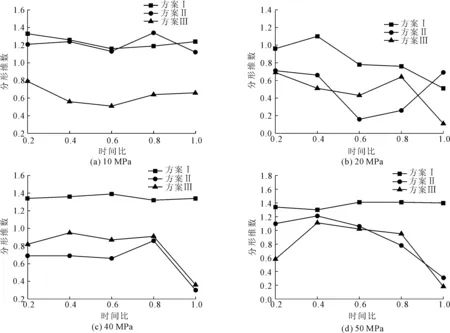
图5 不同时间比下砂岩试样声发射的分形值

岩体的破坏是一个能量耗散过程，室内试样的分形规律与工程岩体的分形规律是统一的。从理论上讲，声发射的分形维数是评价岩体稳定性的有效指标，分形维数低意味着岩体发生工程灾害的可能性较大。在工程应用中，可以建立微震监测系统对岩体的变形和破坏进行实时监测，并利用微震监测得到的声发射信号预测岩体的失稳。

4 结 论

(1) 随着围压的增大，方案I声发射的平静期变得更加明显，这是由于较高的围压限制了新裂纹的产生。随着围压从10 MPa增加到50 MPa，平静期从20 s增加到57 s，裂纹扩展过程由小裂纹的萌生向裂纹聚集过渡。声发射平静期可以看作是常规三轴压缩条件下试样破坏的前兆信息。最大的振铃计数率出现在峰值之后，并随着围压的增大而增大。原因在于试样在围压的束缚下仍然具有一定的承载力，破裂的试样块体一般只有当应力跌落至残余应力才会发生较大的滑移。

(2) 方案Ⅲ的振铃计数率与方案Ⅱ的变化规律相同。与方案Ⅰ不同的是，方案Ⅱ和方案Ⅲ在试样破坏前没有明显的前兆特征，振铃计数率在峰值点达到最大值。

(3) 低围压条件下，应力比为0.8～1.0时，剪切带的形成导致试样脆性破坏，不同应力路径下分形值迅速下降。这一阶段声发射的分形值可以用来研究试样在不同应力路径下的破坏前兆。方案II的分形值递减率最高，方案Ⅲ次之，方案Ⅰ的分形值递减率最低。围压较高时(40 MPa或50 MPa)声发射特征与应力比的关系不明显。

(4) 在高围压条件下，当时间比大于0.8时，卸荷路径下砂岩试样的分形值迅速降低，表明随时间比变化的分形值可以用于高围压条件下岩石破坏的预测。