不同风速谱激励下的风力发电机塔架风致响应及风振系数研究

楚晨晖,陈少林

(1.无锡环境科学与工程研究中心， 江苏 无锡 214000;2.南京航空航天大学 土木与机场工程系，江苏 南京 211100)

风力发电机塔架是典型的高耸薄壳结构，见图1。在其工作环境中风荷载是主要的控制荷载。风荷载是典型的随机性荷载，其风致响应的计算结果除受本身结构特性影响外还有赖于风荷载模型的选择。因此，研究不同风荷载激励下，风力发电机塔架系统的风致响应和风振系数提取具有重要意义。

图1 某兆瓦级风力发电机

对于高耸、大跨等结构的风致响应计算，许多学者做了深入研究[1-4]。风力发电机风致动力响应方面，柯世堂等[5]建立了风轮-机舱-塔体-基础一体化大型风力发电机有限元模型，根据叶素-动量理论考虑了风轮旋转效应对某大型风力发电机全机风振响应和等效风荷载进行了研究。李斌[6]等利用谐波合成法模拟Davenport风谱时程风载，对某格构式新型风力发电机进行了风致响应计算。结果表明，风机塔架的风致响应的脉动效应明显，如采用规范计算格构式风机塔架的风振系数会有效大的误差。霍涛[7]根据气象尺侧数据似合出风机荷载的联合分布函数，并对风机塔筒的结构风致效应和疲劳寿命进行了计算。经研究发现，顺风向和横风向的位移响应规律不一致，并且在考虑最不利风向角工况下的风机疲劳寿命比单一风向角工况下要偏大，证明了风向选取对风机疲劳寿命的影响效应。结构-桩-土相互作用是结构动力分析的重要课题，许多学者在土-结构相互作用方面也做了广泛的研究工作[8-9]。由于风荷载属于典型的随机不确定性荷载，故以不同风速谱作为激励，得出的结构响应也会有所差异。我国规范给出的风振系数计算方法仅适用于形状规则的一般高耸结构。然而，与一般建筑物有所不同，风力发电机塔架是高度高、刚度大、横截面积小的特种结构。由于其特殊的工作形式和复杂的受力特点，规范基于Dvenport单一风速谱激励给出的风振系数计算方法显然不具代表性及精确性。

鉴于此，根据随机振动理论，计算获得不同风速谱激励下的风力发电机塔架脉动响应的功率谱密度，分析了不同风速谱模型选取对风致响应的影响。此外，还讨论了峰因子的合理选取对风振系数的影响，研究结论对实际工程设计具有理论指导和借鉴意义。

1 结构风致响应随机振动理论

风荷载是具有随机性的，通常采用随机振动理论求解结构的动力响应[10-11]。结构运动方程的矩阵表达式为：

(1)

(2)

式中：yi(t)为i节点位移；φij为i节点第j阵型系数；qj(t)是第j振型广义坐标。将式(2)代入式(1)可得到振型坐标系下的广义运动方程：

(3)

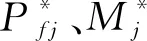
(4)

(5)

式中：wfi为脉动面力；Ai为i节点对应承风面积。Mi为i节质量。由于风荷载f(t)具有随机性，故求解式(3)应输入统计意义下的荷载功率谱密度Sf(zi,ω)，则输出亦为统计意义下的位移功率谱密度Sy(zi,ω)。根据随机振动理论，输出功率谱密度在频谱范围内的广义积分开平方即为均值为零的脉动响应的根方差σy：

式中：角标y表示求解响应物理量为位移，i,k为节点编号，j为振型阶数。σyi为节点位移响应根方差；Sy(zi，ω)为位移响应输出功率谱密度；ω为脉动风圆频率；σyji为j阶振型对应的位移响应根方差；zi为节点高度；H为结构总高度；SFjFj(z,ω)为第j阵型脉动风动力作用的自功率谱密度；Sf(zi,ω)为输入激励功率谱密度；ρik(ω)为i、k节点间的空间相关系数。上式所得结果仅代表脉动响应的均方幅值，结构的总位移响应可由下式计算：

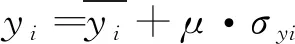
(7)

(8)

2 风力发电机有限元模型

以某兆瓦级风力发电机为参考[12-13]，建立了基础-塔架-机舱-叶片一体化有限元模型。塔架几何尺寸如表1所示；塔身材料采用Q345钢，其具体材料属性如表2所示。风机塔架为典型的薄壳结构，采用SHELL163单元可以很好的模拟其受力状态[14]。塔架有限元模型总计1 500个单元，其中，沿塔架竖直方向划分50单元，环向30单元。

表1 塔架几何尺寸

表2 塔架材料属性

机舱部分对风机整体动力性能影响较小，故采取BEAM189单元对其模拟，共划分12个单元。叶片为三桨叶形式，亦采用SHELL163单元来模拟其薄壳结构。其几何尺寸为宽1.5 m，厚0.3 m，长度32.18 m，共划分114个单元。基础采用混凝土圆形筏基基础。尺寸为：直径10 m，高度1.8 m，单元类型为SOLID65，共720个单元。有关风机基础沉降及基础与地基的土结相互作用，已有学者深入研究[8-9]。为简化模型，基础与地基固接，不考虑土-结相互作用。

最后，将以上各风机各部分构件通过自由度耦合连接在一起，建立了风力发电机一体化有限元模型，单元数总计2 346个，如图2所示。

3 荷载计算

3.1 顺风向脉动风速谱

采用具有代表性的几种不同风速谱作为风力发电机塔架脉动风荷载输入。

图2 某兆瓦级风力发电机有限元模型

(1) Davenport沿高度不变的风速谱[6]

(7)

(2) Harris沿高度不变的风速谱[6]

(8)

(3) Simiu沿高度变化风速谱[6]

(9)

图3 脉动风速功率谱密度曲线

3.2 荷载参数

风场环境采用上海地区近海A类地形，基本风压600 N/m2，10 m高平均风速取31.27 m/s，钢材料阻尼比0.02、混凝土阻尼比0.05。风力发电机塔架表面各角度体型系数[15]见图4，叶片体型系数统一取1.3；高度系数见图5。

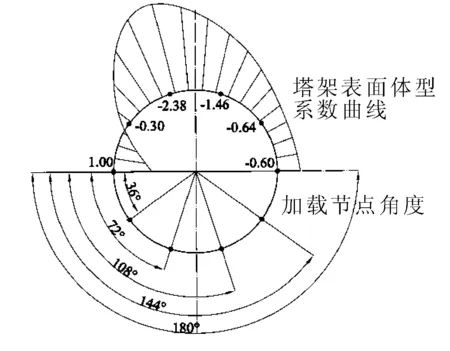
图4 塔架表面体型系数曲线及算例加载节点位置示意图

图5 高度系数变化

脉动风压功率谱由风速谱转化的计算，可由以下公式表示：

(10)

平均风压分别乘以高度系数及体型系数即得到高度Z处平面S节点处节点风压：

(11)

由风压乘以对应面积即得到风荷载。将上述不同风速谱转化成相应风荷载，对风力发电机系统实施顺风向激励，再由前述随机振动理论计算即可得到结构的脉动风致响应。

4 风致响应及风振系数计算及分析

4.1 风力发电机整体模态分析

计算风力发电机动力响应，首先要了解其自振特性。对风机塔架有限元模型进行自振频率计算和模态分析，可得到其各阶固有频率及对应模态振型。其前六阶固有频率如表3所示。

表3 算例风力发电机各阶模态阵型描述及固有频率

4.2 风机塔架风致响应计算与分析

图6—图8给出塔架迎风面方向三个典型测点位移响应的功率谱密度曲线。由图可以看出，在输入风速谱全频域内(0～10 Hz)，三种风速谱激励下的塔架位移功率谱密度曲线(PSD)较为吻合。由图可知，输入三种风速谱，均在第1固有频率(f1=0.173)、第4固有频率(f4=0.258)和第5固有频率(0.429)激发峰值。由模态阵型图可知，第1、5振型均为整体振动主振型；而第4振型为叶片挥舞局部振型，对整体影响较小。风力发电机塔架属于典型高耸结构，如图6—图8所示，在低于1 Hz范围其响应峰值较大，在高频范围内PSD快速衰减。

结合图6—图8及表4所示，一阶振型峰值最高达364.92×10-2m2/Hz，与五、六主阶主振型峰值(0.10 m2/Hz～0.21×0-2m2/Hz)相差悬殊，因此可判断，风力发电机塔架一阶主阵型对低频激励响应的贡献最大。

图6 塔架66.35 m标高迎风面典型测点PSD曲线

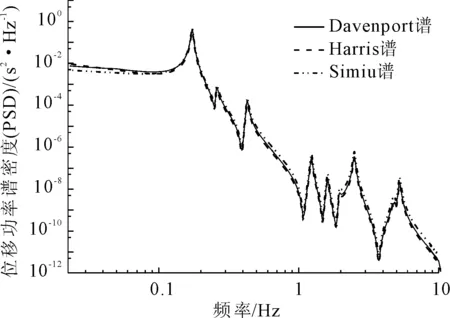
图7 塔架39.81 m标高迎风面典型测点PSD曲线

图8 塔架10.616 m标高迎风面典型测点PSD曲线

表4 不同风速谱激励下66.35 m标高塔架前三阶PSD峰值对比

以66.35 m标高迎风面典型测点PSD三阶峰值数据为例,如图9—图11所示，在不同风速谱激励下，PSD曲线前三阶峰值有所差异，具体表现为Simiu谱峰值最高；Davenport谱次之；Harris谱峰值相对最低。且前三阶自振频率峰值相对差异逐步加大，即一阶峰值三个风速谱峰相对值差异较小；第三阶峰值相对差异增大。其峰值差异如表5所示。

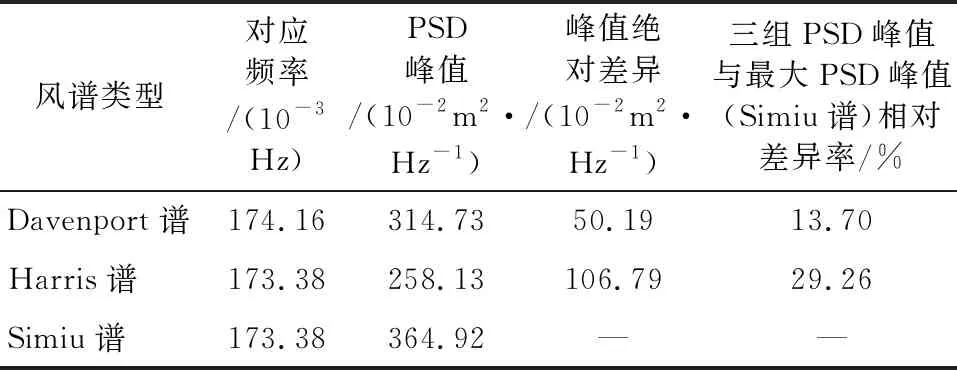
表5 塔架66.35m标高塔架一阶PSD峰值数据对比

图9 塔架66.35 m标高迎风面典型测点第一振型PSD峰值对比

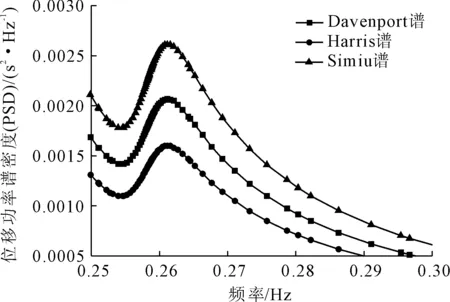
图10 塔架66.35 m标高迎风面典型测点第五振型PSD峰值对比

图11 塔架66.35 m标高迎风面典型测点第六振型PSD峰值对比

图12给出了Davenport谱下的不同高度节点PSD曲线。由图观察，节点PSD曲线在不同高度差异性明显，即脉动响应随结构高度而增加。进一步观察图13可发现，各高度节点前三阶峰值都集中在低频范围内(<1 Hz)。高度较高节点(66.35 m)其PSD曲线在高频范围内几乎不出现峰值；相对而言，中低节点PSD曲线在高频范围内会出现若干共振峰值。即风力发电机塔架不同高度对脉动风荷载的不同频谱段的敏感性明显不同。但如前所述，风机塔架极值响应主要受低频荷载控制，高频共振分量对总体响应的贡献十分有限。所以，工程上分析风机塔架脉动响应仍应以重点关注低频低阶阵型为主。

图12 基于Davenport风谱下的三个典型标高PSD曲线

最后进行定性分析。三种风速谱峰值对应频率分别为：Davenport谱在0.05 Hz附近，Harris谱在0.02 Hz附近，Simiu谱在0.1 Hz附近。本算例中，风机塔架基频f=0.173 Hz，更接近Simiu谱峰值频率范围，因此其激励下结构一阶主振型响应最为剧烈。Davenport谱峰值较高，但频率范围远离塔架基频，因此基于此风谱激励响应次之。Harris谱峰值低，峰值频率亦低，因此激发响应最小。结构风致响应影响因素包括：结构动力性质(刚度、基频、模态)以及风谱参数(峰值和频率)。而结构脉动响应PSD峰值主要取决于结构一阶频率是否接近或达到风速谱峰值频率。

4.3 风机塔架风振系数计算与分析

图13给出了塔架平均位移曲线和脉动响应根方差曲线，由图可见，塔架的脉动响应明显低于平均响应。但考虑乘以峰因子后，平位移与脉动位移水平相当，甚至以脉动响应为主。

计算风振系数首先要确定峰因子的合理取值，Davenport根据极值概率分布理论基于安全度标准提出了峰因子取值的近似计算公式[6]：

(12)

式中：γ为极值系数，可取0.577 2。v可近似取结构一阶自振频率。由模态分析得到一阶频率为v1=0.173 46 Hz。T为风荷载采样的风压时距，我国规范取T=600 s。在低频范围内，峰因子是关于v的单调增函数，取值区间在[3.0，4.5]。根据我国可靠指标的规定，考虑一定跨越概率下μ=2.50；而采用Davenport的极值概率分布理论而推导的公式得到的峰因子为μ=3.24。图14给出了μ理论取值为3.24和规范取值2.50条件下，Davenport谱和Simiu谱激励下计算得到的风振系数。

图13 平均位移曲线与三条风速谱作用下的响应根方差曲线

图14显示了不同峰值系数、不同风速谱激励都会对风振系数计算产生影响。表6分别定量的给出我国规范计算方法μ=2.50，Davenport谱激励和μ=3.24，Simiu谱激励下风振系数计算结构的对比。可以发现不同条件下，二者计算风振系数偏差最大达21.31%，并随高度升高而不断降低，其偏差范围在10%～20%之间。由此可见，选用不同风速谱激励以及不同峰值系数计算风振系数会有较大差异。因此，在实践工程中，脉动风荷载的选取应在有条件的情况下采用根据当地实测风荷载数据化归风速谱，或采用多种类型经典风速谱进行多次试算，同时合理的选取峰值系数，才能较为准确的计算风力发电机高塔系统的风致响应以及风振系数。

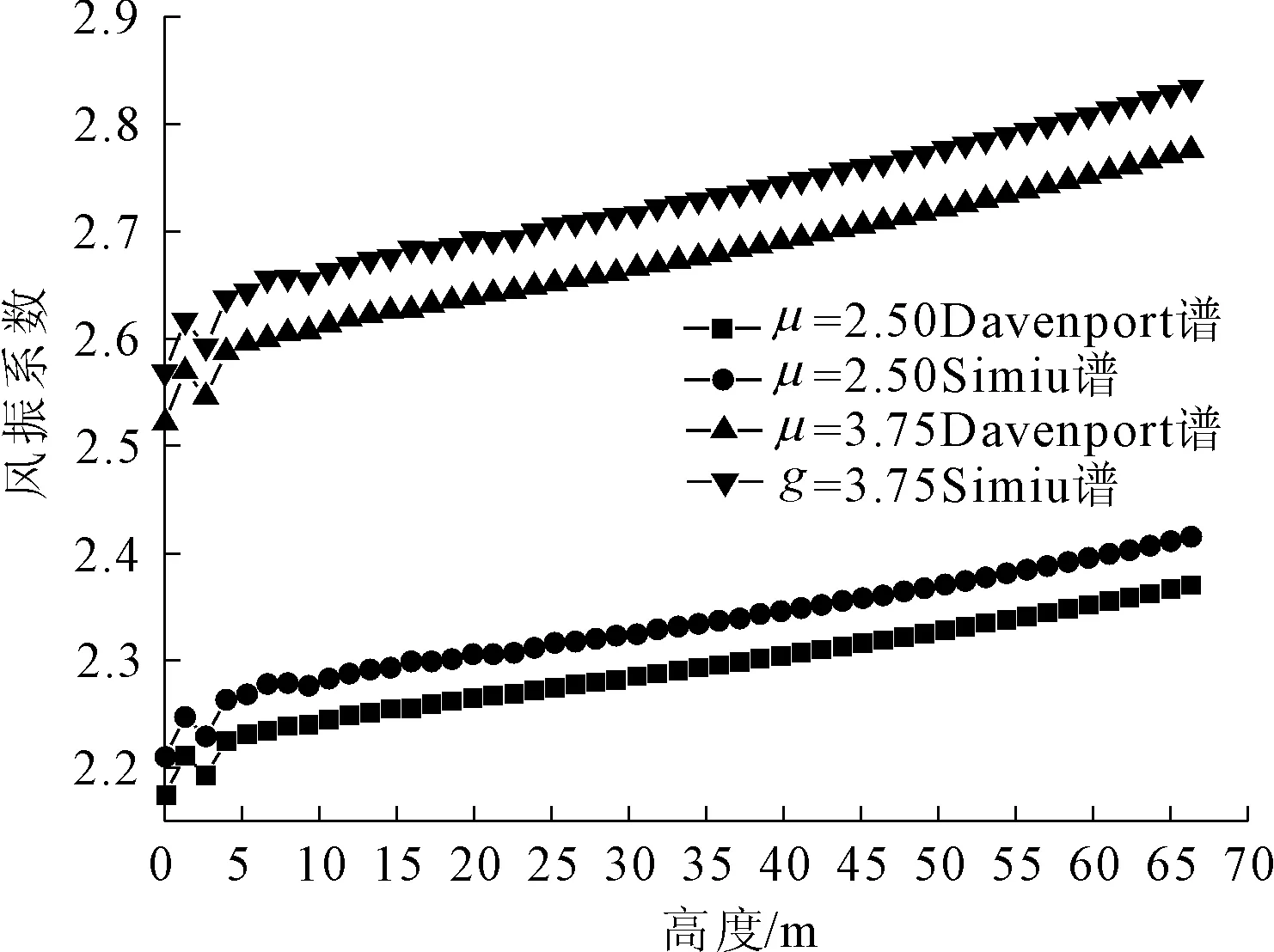
图14 基于不同峰因子取值、不同风速谱激励下风力发电机塔架风振系数规律

表6 基于不同峰因子取值、不同风速谱激励下风力发电机塔架风振系数取值

5 结 论

对某兆瓦级风力发电机进行一体化有限元建模，分别施加不同风速谱模型得到风致脉动响应。分析了不同谱对风力发电机塔架的风致响应计算结果和风振系数取值的影响。得到下述结论。

(1) 在不同风速谱激励下，风力发电机塔架第1、4、5振型(f1=0.173；f4=0.258；f5=0.429)被激发。

(2) 在风速谱全频域内(0～10 Hz),主振型均集中在低频范围内(小于1 Hz)，高频振动对总振动响应影响很小。

(3) 在不同风速谱激励下，Simiu谱PSD曲线谱峰值最高；Harris谱峰值相对最低。风速谱的峰值及峰值频率都会影响结构PSD曲线峰值。而风速谱峰值频率接近或达到一阶自振频率时，激发的结构脉动响应最明显。

(4) 峰因子的取值会直接影响风振系数的计算结果。实际工程计算中应结合技术、经济等综合指标合理确定峰值系数，确保风振系数计算准确安全。