区间毕达哥拉斯模糊幂加权几何Bonferroni平均算子及其应用

蒋莹莹，段鹏举

（宿州学院 数学与统计学院，安徽 宿州234000）

0 引言

1986 年，Atanassov［1］提出直觉模糊集（Intuitionstic fuzzy sets，IFS），随后Atanassov 等［2］对其又进行扩展，于1989 年提出区间直觉模糊集（Interval-valued intuitionstic fuzzy sets，IVIFS），但在决策问题时可能会出现隶属度与非隶属度之和大于1 的情况，致使分析出现偏差. Yager［3-4］引出毕达哥拉斯模糊集（Pythagorean fuzzy sets，PFS）来刻画问题，即隶属度与非隶属度之和大于1的同时其平方和不超过1，其刻画模糊的能力较IFS 强. 2014 年Zhang［5-6］对PFS 进一步扩展，提出区间毕达哥拉斯模糊集（Interval-valued Pythagorean fuzzy sets，IVPFS），很大程度上弥补PFS与IVIFS的不足，取得一些研究成果.

Yager［7］等定义有序加权平均（Order weight average，OWA）算子，Xu［8］等在幂平均（Power average，PA）算子的基础上提出幂几何（Power geometric，PG）算子，同时在PA算子与OWA算子基础上，考虑集成数据间的相互支撑度对权重影响，提出幂调和平均（Power harmonic average，PHA）算子等概念并探讨在群决策中应用. Zhu［9］等在犹豫模糊集（Hesitant fuzzy sets，HFS）环境下通过Bonferroni平均算子且根据属性值的重要程度不同，提出HFWBM 算子和HFWGBM 算子. 张迪［10］等提出区间犹豫梯形模糊几何Bonferroni平均（Interval-valued hesitant trapezoidal fuzzy geometric Bonferroni mean，IVHTrFGBM）算子，并在多属性决策领域中应用.

目前，基于Bonferroni 平均（BM）算子在IVPFS 下多属性群决策成果甚微. 于是，基于Zhang 提出的IVPFS借鉴IVHTrFGBM算子构造IVPFGBM算子，再结合李进军［11］的IVPFPG算子及李晓然［12］的IWGBM算子构造出区间毕达哥拉斯模糊幂几何Bonferroni 平均（Interval-valued Pythagorean fuzzy power geometric Bonferroni mean，IVPFPGBM）算子，同时考虑决策者的偏好、属性的权重影响构造出区间毕达哥拉斯模糊幂加权几何Bonferroni 平均（Interval-valued Pythagorean fuzzy power weight geometric Bonferroni mean，IVPFPWGBM）算子. 本文给出充分考虑决策者之间的相关性及属性指标间的交互性的多属性群决策方法.

1 备用知识

定义1［13］设为论域X 上的一个区间毕达哥拉斯模糊集（IVPFS），其中，分别表示X 上元素x 属于I 的区间隶属度和区间非隶属度，且∀x ∈X，有满足

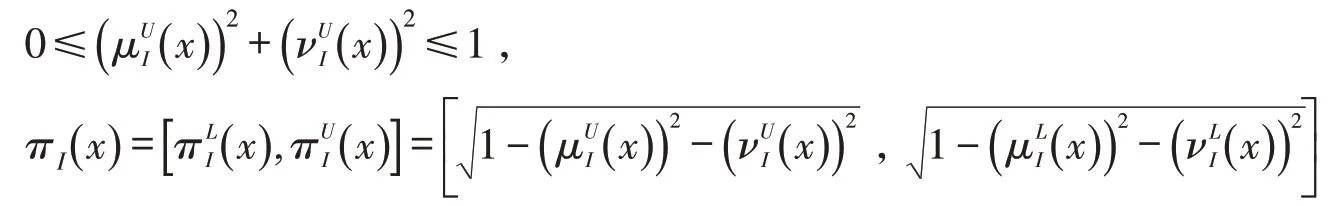
定义2［12］设为任意两个IVPFN，定义如下运算法则：

定义3［12］设为IVPFN，其得分函数与精确函数分别为：

给出如下IVPFN排序方法：

（1）若sα1＜sα2，则α1≺α2；

（2）若sα1＞sα2，则α1≻α2；

（3）若sα1=sα2，有1）若hα1＜hα2，则α1≺α2；2）若hα1＞hα2，则α1≻α2；3）若hα1=hα2，则α1=α2.

1.1 区间毕达哥拉斯模糊幂几何（IVPFPG）算子

定义4［10］设为一组IVPFN，则IVPFPG算子为：

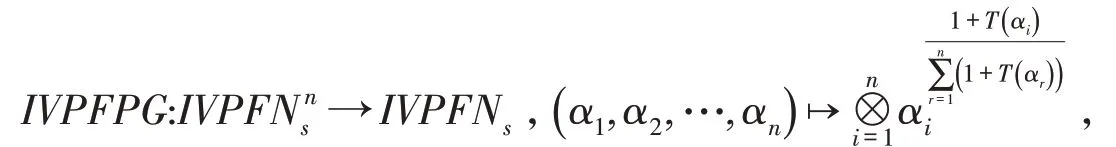
（1）supp(αi,αj)∈[0 ,1] ；

（2）supp(αi,αj )=supp(αj,αi)；

（3）若d(αi,αj )＜d(αs,αt )，则supp(αi,αj )＞supp(αs,αt).

1.2 Bonferroni几何（GB）平均算子

定义5［13］设p,q ≥0，ai≥0(i =1,2,…,n )，则GB算子为：

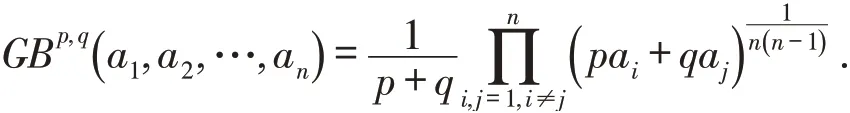
2 区间毕达哥拉斯模糊幂加权几何Bonferroni平均（IVPFPW-GBM）算子

为决策优化，需要在IVPFPGBM 算子的基础上增加决策者间和属性间的支撑度、权重等因素，构造IVPFPW-GBM算子.

定义6设p,q ≥0 ，且不同时为0，为一组IVPFN，权重向量且，则IVPFPW-GBM算子为：

其中T(αi)同定义4.

定理1设p,q ≥0 ，且不同时为0，为一组IVPFN，则IVPFPWGBM算子集成后仍为IVPFN，且

其中

证明令，由定义2得

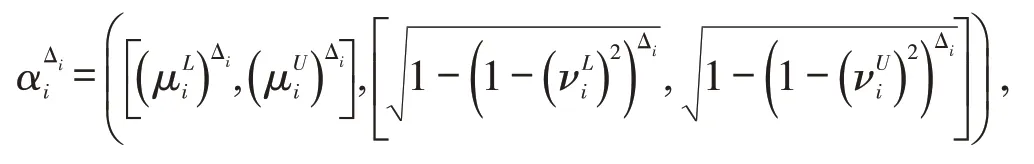
再由运算法则（1）～（4），可得

因此

市场上对客户信用评价的模型良莠不齐，很多评价模型开发企业的产品并没有经过大量数据实验、研究的检验。企业因为缺乏对客户信用信息的足够重视，在判断客户信用时，往往以主观意见及历史交易记录为依据与客户达成交易。

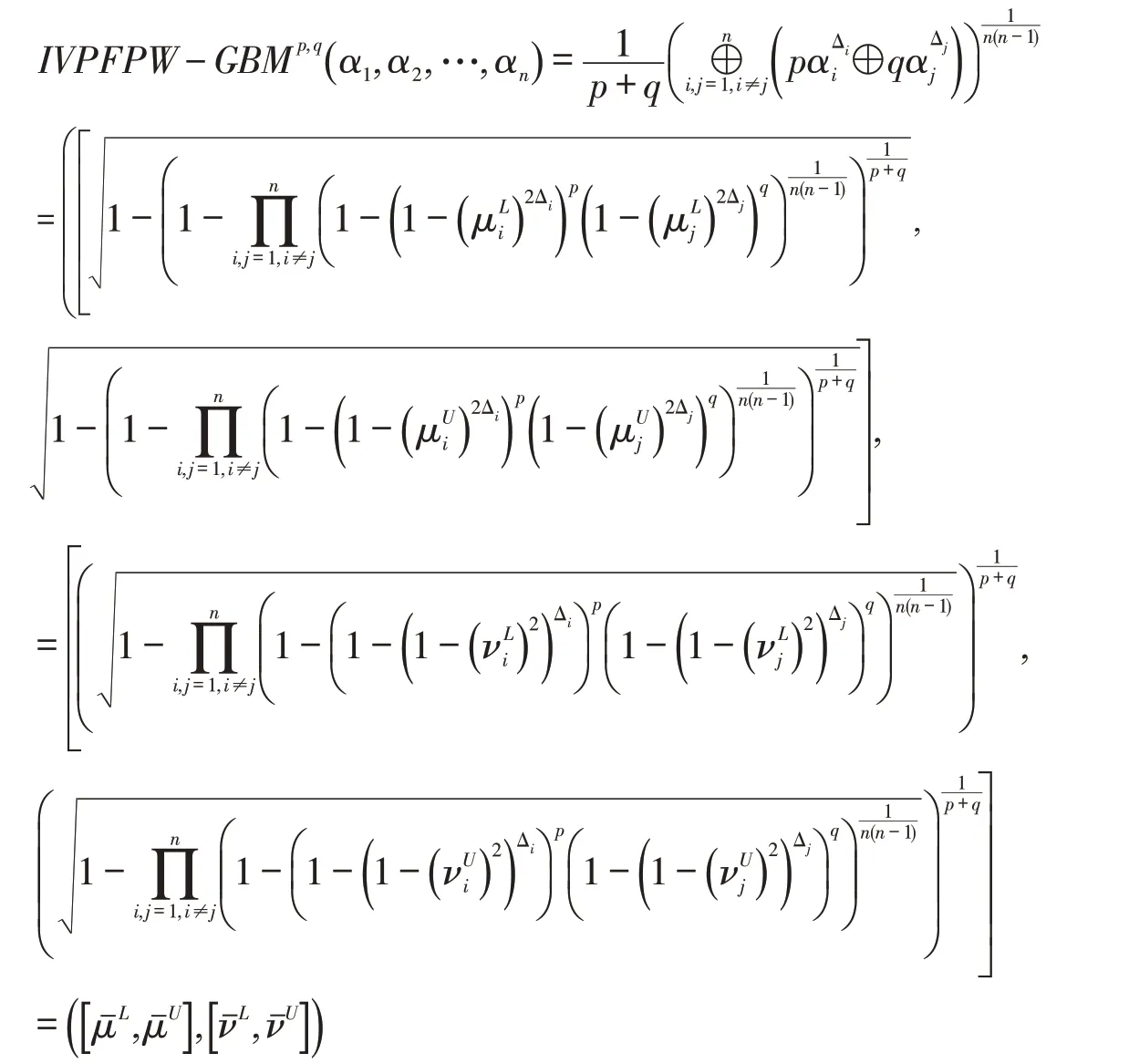
式（1）得证.

定理2设p,q ≥0，且不同时为0，为一组IVPFN，则

（1）幂等性：若αi=α(i =1,2,…,n )，则

（2）置换不变性：设(β1,β2,…,βn)是(α1,α2,…,αn)的任一置换，则

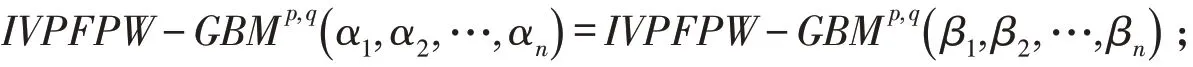
（3）有界性：ξ-≤IVPFPW-GBMp,q( α1,α2,…,αn)≤ξ+，其中

定理2证明过程同定理1，证明略.

3 基于IVPFPW-GBM算子多属性群决策方法

现有IVPFN 环境下多属性群决策问题描述为：候选方案集A={A1,A2,…,Am} ，决策者集且权重向量为，其中λj≥0，=1. 属性集且权重向量为,其中.决策矩阵,其中表示决策者Ek∈E，给出方案Ai∈A 在属性cj下的决策值.

Step1将IVPFN决策矩阵E(k)规范化［6］转化为规范矩阵，其中

Step2算出决策者之间的支撑度，加权支撑度，进而得到的可信度指标

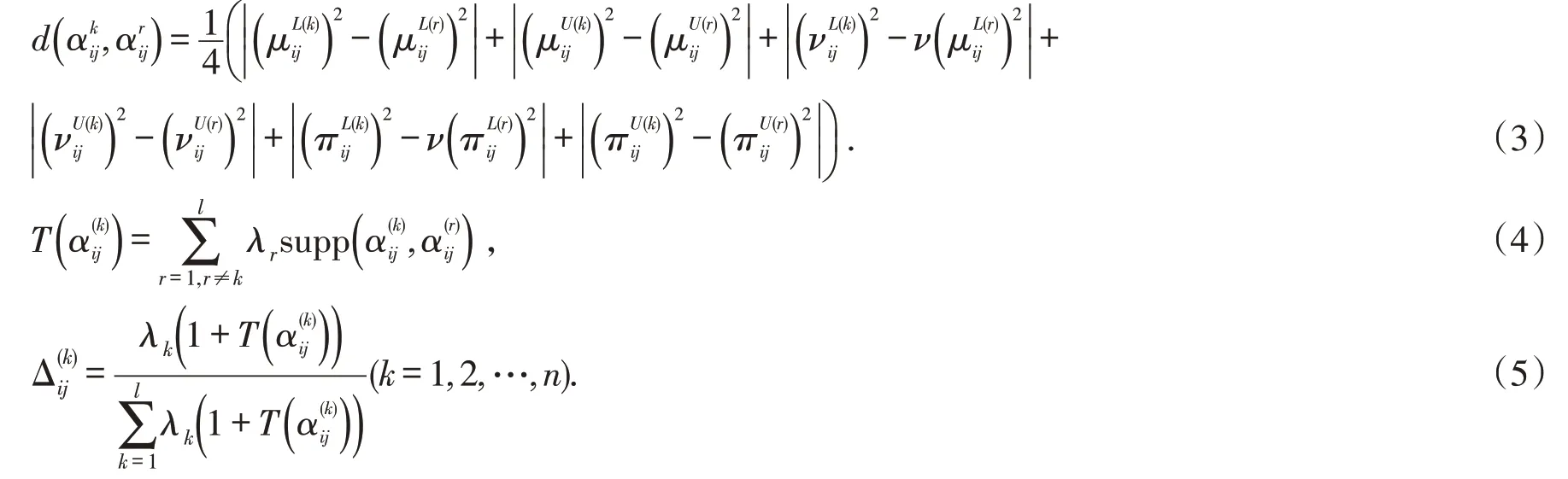
Step3通过IVPFPW-GBM 算子整合决策者的决策矩阵得综合决策矩阵，其中

Step4由式（2）～（5）分别算出属性间的支撑度，加权支撑度T(χij)，进而得到χij的可信度指标Δij.

Step5通过IVPFPW-GBM 算子将候选方案Ai的属性值集成综合属性值ηi:ηi=IVPFPW-GBM(χi1,χi2,…,χin).

Step6计算综合属性值的得分值sηi，对方案进行排序择优.

4 应用实例

企业项目投资，已知有5 个候选方案A={A1,A2,A3,A4,A5} ，所要考虑的评价指标有C={c1,c2,c3,c4} ，分别为：投资报酬率，市场潜力，能源消耗，环境与生态效益；其中各指标的权重向量为ω=(0.3,0.32,0.22,0.16)T. 企业内部选派3名决策者E=(E1,E2,E3)（权重向量为λ=(0.35,0.27,0.38)T）对此3个方案进行评选.

表1 决策矩阵E(1)

表2 决策矩阵E(2)

表3 决策矩阵E(3)

Step1其中c1,c2,c4为效益性指标，c3为成本型指标，将区间毕达哥拉斯模糊决策矩阵( k=1,2,…,5) 规范化为，见表4、表5和表6.

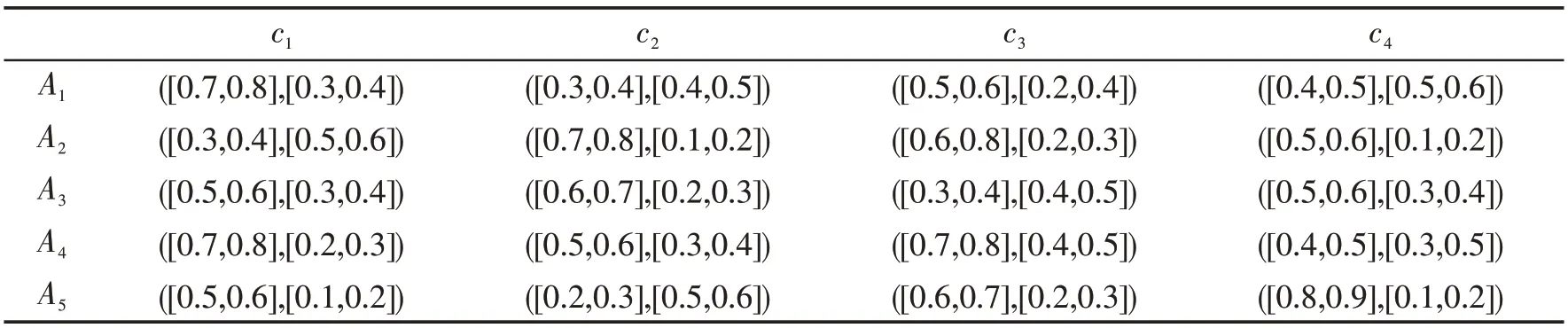
表4 规范化的决策矩阵E(1)

表5 规范化的决策矩阵E(2)

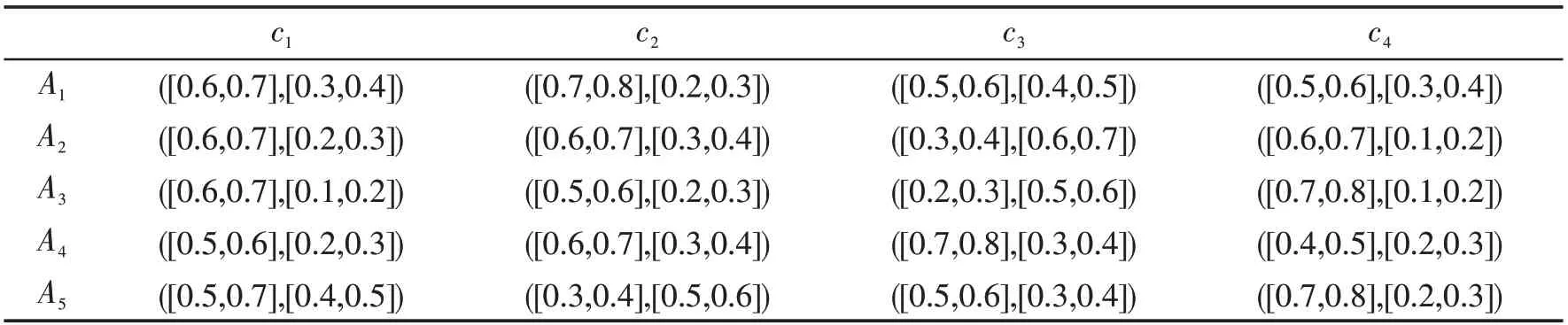
表6 规范化的决策矩阵E(3)

Step2利用式（2）～（5）计算决策者间的支撑度，加权支撑度矩阵，进而得到的可信度指标矩阵

Step3通过式（1）集结决策者的决策矩阵得综合决策矩阵D=( χij)5×4（取p=q=1），见表7.

表7 IVPFPW-GBM算子集成结果

Step4再用式（2）～（5）计算出属性间的支撑度矩阵(j,k=1,2,…,4,j ≠k )，加权支撑度，进而得到χij的可信度指标

Step5再通过式（1）算子将候选方案Ai的属性值集成综合属性值ηi：

Step6用定义3计算综合属性值ηi的得分值sηi: sη1=0.927 7; sη2=0.926 4; sη3=0.944 2;sη4=0.946 6;sη5=0.946 2.

由排序定义可知A4≻A5≻A3≻A1≻A2，即方案A4最优.

5 对比分析

下面讨论IVPFPW-GBM算子参数p,q 对方案排序的影响，见表8.

表8 IVPFPW-GBM算子参数p,q 对方案排序

由表8结果可知，参数p,q 主观选取影响备选方案的排序，但最优结果不变. 纵观整个信息集成决策过程，构造的IVPFPW-GBM算子优点得到充分体现，既充分考虑决策者、属性间的关联性、支撑度等内在联系，又规避奇异值的扰动提高决策的精准度.

6 总结

本文在IVPFN环境下融合PG算子与GBM算子，继承算子能综合决策者间的支撑度集结多个属性值成一个评价值优势，也增加对决策者与属性权重的刻画，提出IVPFPW-GBM算子并讨论其性质. 综合考虑评价值可行性与有效性使得决策过程中充分参考因素间的交互性，避免决策者的偏好风险，较好地提高预测精准度.