一种求解非线性方程组的Levenberg-Marquardt方法及其收敛性

周 童，陈 亮，伍珍香

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

本文主要讨论非线性方程组

的解的问题，其中F( x ):Rn→Rn是连续可微函数. 由于F(x)是非线性函数，方程组（1）可能会没有解，因此本文假设方程组（1）解集非空并设其为X*.

Levenberg-Marquardt 方法（LM）［1-3］是求解方程组（1）的经典方法之一，LM方法通过如下公式给出搜索方向

其中：Fk=F( xk),Jk=F′( xk),μk≥0. 由于是正定矩阵，因此式（2）有唯一解dk，而且搜索方向dk是优化函数

的下降方向，其中φ( x ):Rn→R. 可以证明由LM方法产生的序列的任意聚点是φ 的稳定点，即

因此如果F′( x*)是非奇异的，则x*是方程组（1）的解. 然而对于收敛性来说，F′( x*)是非奇异这一条件过强，因此本文使用局部误差界这一弱条件代替非奇异. 局部误差界定义如下.

定义1设N 是Rn的子集且X*∩N ≠0，如果存在c ≥0，有

成立，则称‖F( x)‖ 为方程组（1）提供了一个在N 上的局部误差界.

对于式（2）参数μk有不同的选择，如当时，Dennis 等［4］给予证明，当μk=‖F( x )‖时，Fan等［5］证明LM的二阶收敛，同时在皆为局部误差界的条件下，也有一些结果，如当μk=αk‖ Fk‖时，Fan［6］证明了局部二阶收敛；当时，杨柳等［7］证明局部二阶收敛；当（0 ≤θ ≤1）时，Ma［8］证明局部二阶收敛；当时，张华仁等［9］证明局部二阶收敛；当μk=‖ Fk‖2时，Yamashita等［10］很好地证明LM二阶收敛，由于参数的选择使算法的迭代次数过多，因此，本文对参数进行了改进，使其迭代次数减少. 在本文中设

与文献［10］相比，由于考虑了‖ Fk‖的取值情形，使参数总是小于等于1，避免迭代步过大，提高计算效率，数值实验也显示了迭代次数减少.

1 LMM的收敛速率

本节研究LM方法的局部收敛性，公式为

其中dk是线性方程（2）的解.

定义一个二次函数

其中：θk:Rn→R，Fk=F(xk),Jk=F′( xk). 由于函数（8）是严格凸的，所以无约束最小值问题

等价于线性方程（2）. 为证明LM方法的收敛性，先给出一些假设条件.

假设1对于x*∈X*，以下条件［11］（i）和（ii）成立：

（i）存在b ∈( 0,1),c1∈(0,∞)，有

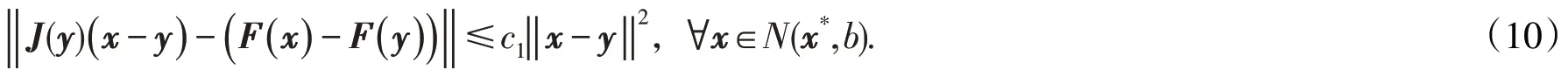
（ii）如果存在一个常数c2∈(0,∞)，使得

则称对于式（1），‖F( x )‖在N( x*,b) 上提供一个局部误差界.

当F 是连续可微的且J 是Lipschitz连续的，由假设1（i），存在一个常数L，使得

在上述假设和LM参数的设定下，证明以下引理.

引理1设假设1成立，则存在常数p,q，使得

证明下面分2种情况讨论.

第1 种 情 况：当‖ Fk‖≤1 时，μk=‖ Fk‖δ. 由 假 设1（ii）知，c2dist(x,X*)≤‖ F( x )‖，所 以，又由式（12）知，‖ F( x )-F( y )‖≤L‖x-y ‖，因为μk=‖ Fk‖δ，所以有μk≤Lδdist(xk,X*)δ.

第2种情况：当‖ Fk‖＞1时，μk=‖ Fk‖-δ＜1. 由上式可得，μk≥L-δdist(xk,X*)-δ.

引理2设假设1成立且参数μk由上述给出，如果，则式（2）的解dk满足

证明由于dk是式（9）的解，所以有

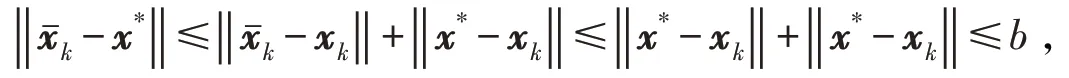
假设{ xk} 收敛到x*，秩［12］(J(x*))=r，将J(x*)进行SVD分解

由于‖ Fk‖的不同，下面将分成2种情况讨论.

1.1 第1种情况：‖ Fk ‖≤1

引理3假设F(x)是连续可微的，J(x)和F(x)是Lipschitz连续的，则

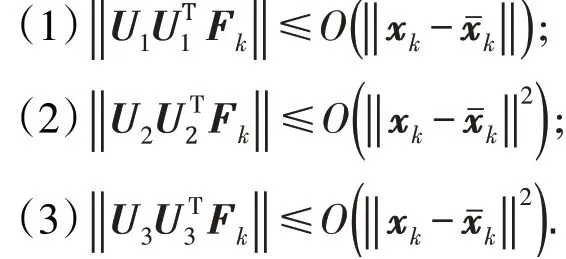
证明证明过程与文献［13］引理4.1的证明类似，这里不予证明.

引理4假设F(x)是连续可微，J(x)和F(x)是Lipschitz连续的，则

证明通过Jk的SVD分解，有，并且有

因为假设{ xk} 收敛到x*，假设，因此当‖ Fk‖≤1时，

引理5如果，则有

证明由条件知,，且xk=xk-1+dk-1，因此由假设1（i）（ii）和引理2可以得到

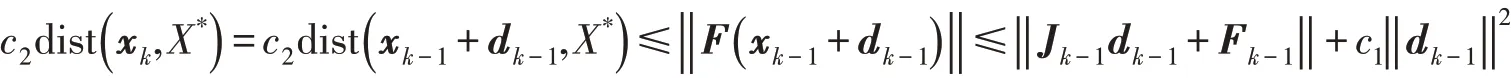
由引理4知，存在常数c4＞0，有，所以

引理6如果x0∈N(X*,r1) ，则对于所有的k，有

证明由数学归纳法知，当k=0 时，由引理2有

所以有xk+1，引理得证.

下面将给出LM方法的二阶收敛性定理.

定理1若假设1成立，x0∈N( X*,r1) ，且{ xk} 是由LM方法产生的一组序列，则{dist(xk,X*)} 二次收敛到0，同时序列{ xk} 收敛到解

证明引理3和引理4已经证明定理的第1部分. 接下来只需要证明定理的第2部分，即序列{xk} 收敛到解. 因为收敛到0且对于所有的k，有，足以说明{xk}收敛. 因为对于所有k ≥1,有，所以任意i,j ∈N+,i ≥j，有

这意味着序列{ xk} 是Cauchy序列，因此{ xk} 收敛.

1.2 第2种情况：‖ Fk ‖＞1

引理7如果xk,xk-1，dist(xk-1,X*)≤r2＜1，则有

证明由条件知，，且xk=xk-1+dk-1，由假设1（i）（ii）和引理2可以得到

又因为

所以当‖ Fk‖＞1时，

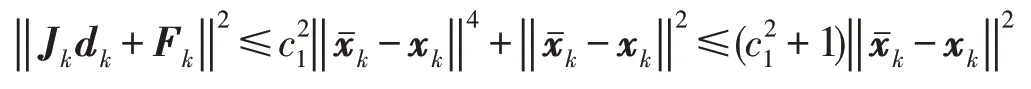
故

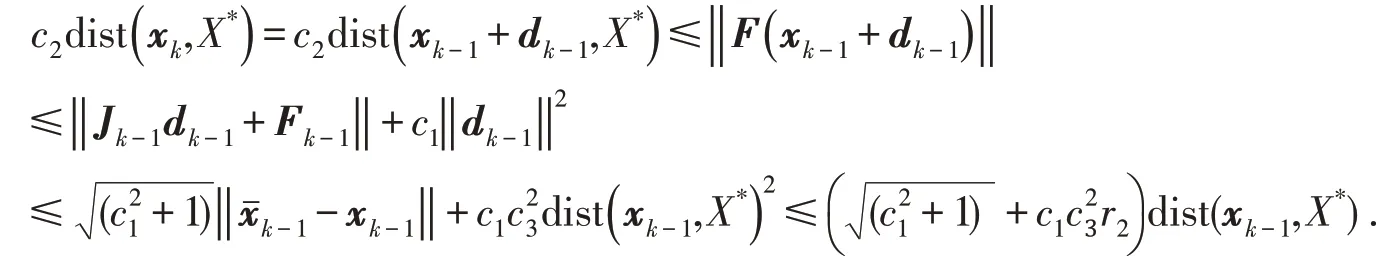
所以dist(xk,X*)≤c5dist(xk-1,X*)，其中，引理得证.

引理8如果，则对于所有的k，有

证明由数学归纳法知，当k=0 时，由引理2有

则

定理2设假设1成立，且是由LM方法产生的序列，则线性收敛到0，同时序列{ xk} 收敛到解

证明证明过程与定理1证明类似，省略.

2 数值结果

在本节中，本文要进行数值实验用来验证文章中所提出的自适应性Levenberg-Marquardt方法，LM方法的算法在文献［9］给出，它选择参数μk=‖ Fk‖2很好地证明了二阶收敛，但迭代次数过多，因此本文进行改进，使迭代次数减少.

考虑由非奇异问题［14-15］改编的非线性方程组，其中：F( x )是标 准的非奇异测试 函 数，x*是其 根，A ∈Rn×k是列 满 秩，1 ≤k ≤n. 很容易看出，且的秩为n-k. 问题的不足之处是使的解可能不是F(x )=0 的解. 现在考虑的秩为n-1的奇异问题.

下面给出相关矩阵，A ∈Rn,AT=(1 ,1,…,1) .

根据在LM 方法和ALM（Adaptive Levenberg-Marquardt,ALM）方法中定义的δ 的不同，本文将在LM方法中取δ 为2，ALM 方法分别取δ 为1，1.5 和2. 2 个算法终止条件是相同的，都是，或者迭代次数不超过100（n+1），则对于秩为n-1 的数值结果为表1. 在第3 列中的1，10 和100 与起始点x0，10 x0和100 x0相联系，其中x0被建议使用［14］. 如果相应的方法在规定的最大迭代次数内失败于达到所需的精度，则用“-”表示. 为保障数值的稳定性，需要使用MATLAB中的pcg函数来解决式（2）的问题.

从2个算法的直观结果来看，在LM方法中x0=1 或10时迭代次数较少，但当x0=100 时算法收敛但迭代次数较多，而ALM方法将参数重新选择，则在所需的最大迭代次数内收敛时的迭代次数要少于LM方法的迭代次数，尤其是指数同为2时，可以得到ALM方法的有效性.

表1 Rank( J( x* ))=n-1

3 总结

本文主要介绍用具有自适应性参数的Levenberg-Marquardt方法解非线性方程组问题，研究它的收敛性，证明出在局部误差界的条件下当‖Fk‖≤1 时其二次收敛，当‖Fk‖＞1 时其线性收敛，最后也通过数值试验验证出方法的有效性.