基于粒子群算法的投影孪生支持向量机

叶黎明，陈素根

（安庆师范大学 数理学院，安徽 安庆246133）

0 引言

支持向量机（Support Vector Machine，SVM）是一种经典的机器学习的算法［1］，它最初是由Vapink 等人提出的一种用于解决分类问题的算法，由于SVM具有较强的理论基础和较好的泛化能力而被广泛应用［1］. 在解决二分类问题上，SVM依据的是在特征空间中寻找间隔最大化的分类超平面. 2006年，广义特征值近端支持向量机（Proximal Support Vector Machines Via Generalized Eigenvalues，GEPSVM）［3］的出现，使得支持向量机的研究进入新篇章. 受GEPSVM算法的启发，Jayadeva等人于2007年提出孪生支持向量机（Twin Support Vector Machine，TWSVM）［4］. 实际上，TWSVM求解两个规模较小的凸二次规划问题代替SVM中一个规模较大的凸二次规划问题，提升训练性能，理论上使训练速度变成SVM的4倍. 从此，诸多学者对TWSVM 及相关算法开展深入研究，取得丰硕的成果［5-6］，PTSVM 就是具有代表性的研究成果之一［7］. 该算法的思想是找出2个最优的投影方向，使得本类样本投影之后尽可能聚集在该类的投影中心周围，同时另一类样本投影之后尽可能远离该投影中心. 随后，许多学者在PTSVM的基础上提出各种改进算法［8-10］，丰富PTSVM的研究.

尽管对于PTSVM的研究还在持续不断地进行着，它的性能也在不断地加强，但在参数选择上仍存在不足之处，且参数的好坏对于PTSVM 性能有较大影响. 为提升算法的性能，智能算法逐渐被引入到TWSVM算法中，丁世飞等人将粒子群算法（PSO）［11］和量子粒子群算法（Quantum Particle Swarm Optimization，QPSO）［12］与TWSVM结合，分别提出基于粒子群算法孪生支持向量机［13］和量子粒子群算法孪生支持向量机［14］. 之后，受上述文献启发，李景灿等人提出基于人工鱼群算法（Artificial Fish Swarms Algorithm，AFSA）的孪生支持向量机［15］. 另一方面，PSO是一种基于全局式搜索的群智能优化算法，该算法不但设计原理简单、计算量比较小、编程容易实现，而且由于PSO能够在多维空间中可以有效地对惩罚参数进行分析优化，并具有收敛快、求解质量高的特点. 因此，粒子群算法被广泛应用于各种研究问题［16-18］的参数优化中，并取得不错的实际应用效果. 基于上述分析，本文尝试将粒子群算法与PTSVM相结合，提出基于粒子群算法的投影孪生支持向量机，解决PTSVM惩罚参数和核参数选择问题，提升算法性能，并在UCI数据集上验证算法的有效性.

1 相关理论

1.1 投影孪生支持向量机

假设2类样本集合分别表示为：

其中，m1和m2分别为正类(+1) 和负类( -1) 样本数，并且令m=m1+m2，m为样本总数量，再假定n为样本维度. PTSVM是寻找两个最优的投影方向w1和w2，并最小化同类的投影样本的类内方差，并使另一类的投影样本尽可能分散. PTSVM算法的具体问题如下：

其中：C1和C2是非负惩罚参数，ξk和ηk是非负松弛变量.

为简化上述表达，给出以下定义.

在求解式（1）和式（2）中，引入拉格朗日函数，结合KKT（Karush-Kuhn-Tucker）条件，再结合式（3）和式（4），将优化问题转化为对偶形式：

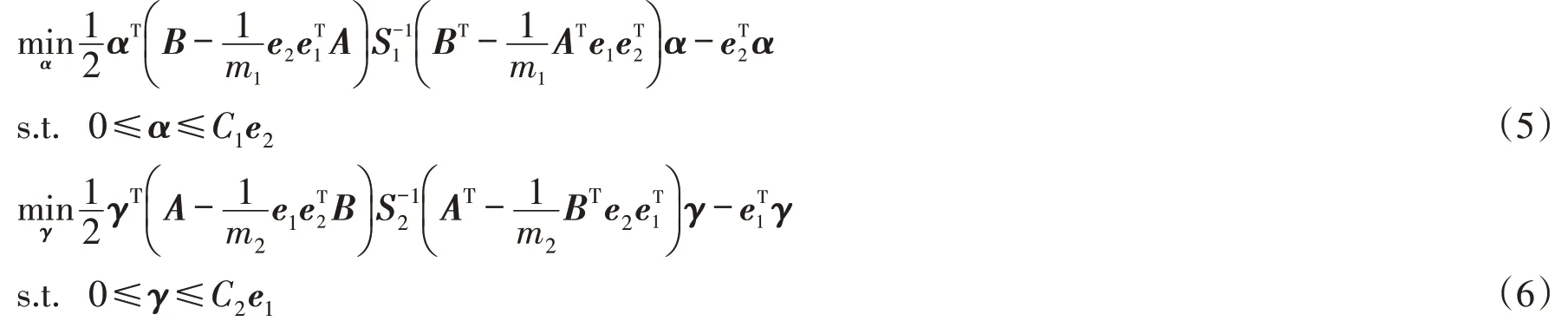
其中：α和γ是拉格朗日乘子，，A和B为正负类样本集合. 求解式（5）和式（6），得到w1和w2. 对于未知样本x∈Rn，其决策函数为：

对于非线性PTSVM，将原空间映射到高维特征空间，则式（3）和式（4）中S1，S2改为：

其中：K 为特定的核函数，CT=[AT,BT]. 类似于线性PTSVM的方式，得到：

于是，得到相应的决策平面为：

其中：X1=A,X2=B.

1.2 粒子群算法

PSO算法可以简单描述为：假设有N 个微粒在种群中，种群中粒子i 在d 维的搜索空间中第t 代的位置可以用一个d 维向量表示，粒子i 的速度和位置通过式（13）和式（14）快速迭代更新.

其中t 为粒子更新迭代次数. 在d 维空间中第t 代粒子i 所经历的“最好”位置记作“最好”的粒子位置记作，c1和c2为加速系数，w 为惯性系数，c1、c2、w 都是固定值.r1和r2是2个在区间[0,1]范围内随机变化的数. 粒子经过不停更新迭代学习，最后达到d 维空间中解的全局最优位置，最终输出的gb 就是算法找到的全局最优解. 图1是粒子群算法的流程图，该图直观地叙述粒子群算法的运行步骤.

图1 粒子群算法流程图

图2 PSO-PTSVM算法流程图

2 基于粒子群算法的投影孪生支持向量机

投影孪生支持向量机需要寻找2个最优投影方向w1和w2，在线性PTSVM中，需要对2个惩罚参数进行优化确定，在非线性PTSVM中，除惩罚参数外，还有核参数需要确定. 网格搜索是常用的参数选择方法，但该方法会花费很多时间，而且这种穷举搜索过多依赖于调参设置，极大地影响分类结果的准确性.而PSO算法的全局参数优化能力将克服网格搜索方法的缺点，受其启发，本文提出一种新的算法：基于粒子群算法的投影孪生支持向量机（PSO-PTSVM）. 将PSO算法引入到PTSVM中，通过PSO算法对PTSVM的多个参数进行寻优，这样不仅能提高PTSVM的分类精度，同时又能大幅度降低PTSVM的运行总时间.下面给出PSO-PTSVM的具体步骤：

Step1 将粒子群规模N 和最大的迭代次数K 设置为固定的数值，将PTSVM中所需优化的参数当作粒子群中需要初始化的个体，并计算出初始化后所需优化的粒子速度和方向. 将初始化后的粒子代入到投影孪生支持向量机中，对训练集进行分类，计算出分类精度，然后将分类精度设置成适应度值.

Step2 根据式（13）和式（14），不断在全局中更新粒子的速度和方向，同时计算粒子新的适应度值，将产生的更好适应度值替换原来的适应度值，如果更新后某个粒子的最优适应度值比当前全局的最好适应度值更优，那就更新全局最优值.

Step3 假如迭代次数已经达到Step1中设置的固定数值，那么就终止迭代. 否则，重复执行Step2.

Step4 最终得到最优适应度值，将其对应的数值作为投影孪生支持向量机的参数值，得到最优的分类精度，这就构成PSO-PTSVM模型.

图2给出PSO-PTSVM 算法的流程图.

3 实验结果及分析

为验证PSO-PTSVM 的性能，选取8个UCI 数据集进行实验，表1给出数据集的特征. 具体实验环境是MATLAB R2018a，硬件配置为Window10操作系统，16 GB内存，AMD和3.40 GHz主频CPU的计算机.实验中，选取TWSVM，PTSVM和AFSA-PTSVM作为对比实验，与PSO-PTSVM进行比较. 非线性实验中，选取Gauss径向基核函数K( x,y )=e-μ‖x-y‖2，其中μ 为核参数.

表1 实验数据集的特征

实验阶段，在TWSVM、PTSVM、AFSA-PTSVM 和PSO-PTSVM 中，对每个数据集都采用10-折交叉验证方法，实验结果给出平均分类精度和运行总时间. 在TWSVM 和PTSVM 中，C1,C2和μ 的网格搜索范围均设置为{2i|i=-8,-7,-6,…,6,7,8} ，AFSA-PTSVM 中，最大尝试次数try_number、视野Visual、步长Step、拥挤度因子δ、最大迭代次数K 、种群规模N 分别设置为5、0.5、0.1、0.618、50、10. 基于实验公平性考虑，PSO中K 和N 的设置和AFSA一样，2个学习因子η1=η2=2，惯性权重ω=0.8. 图3和图4分别给出线性和非线性PSO-PTSVM在Australian数据集上的收敛曲线，其中横坐标和纵坐标分别表示迭代次数和分类精度. 从图3和图4可以看出，该算法收敛速度快，大概只需15次迭代就收敛.

表2 和表3给出线性情况下比较结果，表2是4种算法的分类精度和方差，表3是4种算法在不同数据集上运行的总时间. 表4给出非线性情况下4种算法的分类精度和方差的比较结果，表5给出非线性情况下4种算法在不同数据集上运行的总时间. 为体现算法的优越性，将最高分类精度和最短的运行总时间用加粗数字标出.

图3 Australian数据集线性结果

图4 Australian数据集非线性结果

观察表2～表5的结果可以发现，在线性分类情形下，PSO-PTSVM都获得较好的分类结果，其分类精度都高于其他3个算法；非线性分类情形下，PSO-PTSVM 在大多数数据集上取得较好的分类精度，仅在Liver、Ionosphere 和Wpbc 3 个数据集上比AFSA-PTSVM 略差一点，但仍然比TWSVM 和PTSVM 效果好.从表3和表5可以看出，在线性和非线性情形下本文提出的PSO-PTSVM运行总时间更短. 为便于观察实验结果，图5和图6给出分类精度，易知本文提出的PSO-PTSVM比TWSVM、PTSVM以及AFSA-PTSVM 3种算法具有更好的分类性能.

图5 线性情形下分类精度

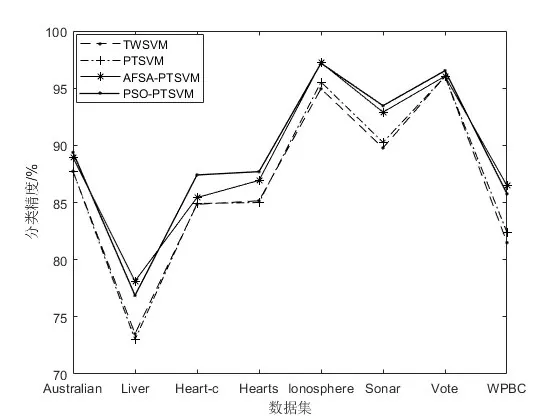
图6 非线性情形下分类精度

表2 线性模式下4种算法的实验比较

表3 线性模式下4种算法运行时间比较

表4 非线性模式下4种算法的实验比较

表5 非线性模式下4种算法运行时间

4 结论

本文针对投影孪生支持向量机（PTSVM）算法运行时间过长和最优参数选择困难的问题，提出基于粒子群算法的投影孪生支持向量机（PSO-PTSVM）. 利用粒子群算法快速高效的搜索能力，对PTSVM算法中的多个参数进行优化，避免参数选择的盲目性. 在UCI 数据集上进行实验，与TWSVM、PTSVM 和AFSA-PTSVM算法对比，PSO-PTSVM运行总时间短且具有更好的分类性能. 但不足之处在于，粒子群算法容易陷入局部最优，如何将新型智能算法用于解决投影孪生支持向量机的参数选择问题，并构建高效的全局最优算法，依然值得进一步研究.