比特切片型算法差分及线性特征的快速构造*

崔雅馨, 徐 洪, 戚文峰

信息工程大学, 郑州450001

1 引言

分组密码是密码学的重要分支, Feistel、SPN、Lai-Massey 等是常见的分组密码算法结构. 以AES算法为典型代表, SPN 结构通常是由两个重要组件构成: 非线性函数S 和可逆线性变换P. 非线性函数S 作为混淆层, 可逆线性变换P 则发挥扩散作用. 除AES 算法外, Serpent[1]、ARIA[2]、PRESENT[3]、RECTANGLE[4]、Skinny[5]、GIFT[6]以及我国分组密码算法竞赛提交的uBlock[7]、FESH[8]、TANGRAM[9]等都是来自SPN 结构的典型算法.

比特切片技术起初由Biham 等人[10]在1997 年提出用于加速DES 算法的软件实现效率, 之后Anderson 等人采用比特切片的思想设计了Serpent 算法[1]. 比特切片技术主要优势体现在可以高效提升算法的软件实现性能: 对于n 个S 盒并置构成的混淆层,每个S 盒需要查表一次,整个混淆层需要做n 次查表操作, 可以把S 盒每个输出比特通过输入比特的若干逻辑指令计算得到, 如果每个S 盒是相同的, 则对于n 个S 盒的相同位置比特只需要一次相同的逻辑指令计算完成. 对于RECTANGLE、TANGRAM等扩散层采用行循环移位的比特切片型分组算法, 本文将利用其结构特点, 对其安全性做进一步分析.

差分分析和线性分析是分组密码最重要的两类分析方法. 如何求解最小活动S 盒数目以估计差分概率(线性偏差) 的安全界, 和如何寻找具有最大差分概率(线性偏差) 的密码特征是其中面临的关键问题.2011 年, Mouha 等人[11]利用混合整数线性规划方法(mixed integer linear program, MILP) 给出了基于字节的最小活动S 盒个数的自动化搜索. 随后, 孙思维等人[12,13]进一步扩展了Mouha 等人的想法,提出了基于比特的MILP 模型, 将S 盒的具体差分样式转化为相应的不等式组, 更加精确地刻画最小活动S 盒个数和最优差分特征. 此后MILP 自动化搜索技术被广泛应用于求解各类算法的区分器. 2016 年,Xiang 等人[14]建立MILP 模型, 搜索SIMON、PRESENT 等6 个轻量级算法的积分区分器. 2018 年Zhu 等人[15]利用MILP 自动化搜索技术, 提出两阶段搜索策略求解GIFT 差分特征. 2019 年Zhou 等人[16]通过分别征服的思想提出了基于MILP 技术的搜索算法, 搜索了PRESENT、TWINE 等算法的差分特征.

对于分组规模较小的分组算法, 借助求解器的强大资源, 可以实现遍历所有可行域寻找最优解, 实现效率大大提高, 取得了一系列较好的研究成果. 但是针对分组规模较大的算法, 对于个人现有的计算资源, 利用MILP 建模直接去求解高轮数的特征, 在有效时间内实现还是困难的. 对于RECTANGLE、TANGRAM 等扩散层为行循环移位的比特切片型算法, 我们希望利用算法本身的结构特点和S 盒的差分(线性) 性质, 尝试构造单轮或低轮迭代特征, 并结合MILP 自动化搜索技术高效构造长轮数的差分和线性特征.

本文中我们引入单轮循环差分(线性) 特征的概念, 针对RECTANGLE 型比特切片型算法, 根据算法的行移位参数和S 盒的可逆差分(线性) 对, 给出了快速构造单轮循环差分(线性) 特征的方法. 进而以找到的单轮循环特征为基础, 结合MILP 方法找到了一些具有特定输入和输出的低轮最优差分(线性) 特征, 由此快速构造了一些长轮数的差分(线性) 特征. 进一步, 针对可逆差分(线性) 对概率优势不明显的算法, 搜索了更优的低轮循环差分(线性) 特征. 对于RECTANLE 算法, 可以构造概率为的循环差分特征和线性相关度为的循环线性特征, 最后可以分别得到14 轮差分特征和13 轮线性特征; 对于TANGRAM算法, 可以构造两种类型的线性相关度均为的循环线性特征, 两种类型的概率为的循环差分特征. 进一步,找到了TANGRAM 128 算法的三种类型概率均为的3 轮循环差分特征, TANGRAM 256 算法的3 轮循环差分特征, 以及2 轮和4 轮循环线性特征. 最终, 可以快速构造出TANGRAM 128 算法的24 轮差分特征和23 轮线性特征, 均与作者设计文档中所给出的最优差分和线性特征的概率相同. 并且可以快速构造出TANGRAM 256 算法的48 轮差分特征和44 轮线性特征, 其中算法设计者仅给出了直到29 轮最优线性特征的概率.

本文主要安排大致如下: 第2 节介绍必要的预备知识和涉及的相关符号, 第3 节详细介绍了如何快速构造单轮循环特征及构造所需的条件, 第4 节针对RECTANGLE 和TANGRAM 算法, 运用循环特征快速构造方法构造了更长轮数的差分和线性特征, 第5 节简要总结本文的主要工作.

2 预备知识

2.1 RECTANGLE 算法

RECTANGLE 算法[4]是由张文涛等人于2015 年提出SPN 结构的轻量级分组密码算法. 该算法采用比特切片的设计思想, 便于多平台的软硬件实现. 算法分组长度为64 比特, 密钥长度为80 比特或128比特, 迭代轮数为25 轮. 每轮轮变换主要包含三个步骤: 密钥加、列代替和行移位.

设RECTANGLE 算法某轮的输入状态为w = (w63w62···w0), 则它可以用图1 所示的4×16 的矩型数组表示, 或者用二维数组(ai,j) 表示, 其中0 ≤i ≤15, 0 ≤j ≤3. 为表述方便, 我们也常用各列对应的16 进制整数(a15a14···a0) 表示状态w.

图1 RECTANGLE 算法的轮状态及其二维表示Figure 1 State of RECTANGLE and its two-dimensional representation

密钥加: 轮状态w 和轮子密钥K 逐比特异或加.

列替换: 每轮采用十六个相同的 4 比特 S 盒并置, 分别同时作用于每列 4 比特状态, 得到S(ai,3,ai,2,ai,1,ai,0), 其中所采用的S 盒是4 比特到4 比特的双射, 具体描述见表1.

表1 RECTANGLE 算法的S 盒Table 1 True table of S-box of RECTANGLE

行移位: 以行为单位进行整体的左循环移位, 第一行保持不动, 第二行循环左移1 比特, 第三行循环左移12 比特, 第四行循环左移13 比特.

2.2 TANGRAM 算法

TANGRAM 算法[9]是张文涛等人提交分组密码算法竞赛的入选算法, 其整体设计思想延续了RECTANGLE 算法, 但是分组长度较大, 包含128 比特和256 比特两个版本, 其中TANGRAM 128算法密钥长度可选128 比特和256 比特两种. TANGRAM 128/128 算法总轮数为44 轮, TANGRAM 128/256 算法为50 轮, TANGRAM 256/256 算法则为82 轮. 每轮操作和RECTANGLE 算法类似, 采用了不同的S 盒和行移位变换, 其中S 盒的具体描述见表2.

行移位变换时, TANGRAM 128 算法保持第一行不动, 第二行循环左移1 比特, 第三行循环左移8 比特, 第四行循环左移11 比特, 即相应的移位参数分别为0, 1, 8, 11. 而TANGRAM 256 算法的行移位参数分别为0, 1, 8 和41.

表2 TANGRAM 算法的S 盒Table 2 True table of S-box of TANGRAM

2.3 符号说明

n: 每轮S 盒个数;

Si: 第i 个S 盒, 0 ≤i ≤n −1, 最左边为第n −1 个S 盒;

a: S 盒的输入(或者输入差分) 对应的16 进制整数;

b: S 盒的输出(或者输出差分) 对应的16 进制整数;

ai: a 的第i 比特, 0 ≤i ≤3 , 其中a0为最低比特位;

lj: P 变换中第j 行的行移位比特数, 0 ≤j ≤3.

3 单轮循环特征的快速构造

对于RECTANGLE、TANGRAM 等算法, 由于其扩散层为简单行循环移位, 当S 盒具有特定的差分/线性性质时, 可以方便构造相应的单轮循环差分/线性特征. 为此, 先引入两个重要概念.

定义1 (S 盒的可逆差分对) 对于4 比特的S 盒, 若存在一对非零比特串a = (a3a2a1a0) 和b =(b3b2b1b0), 使得: 当S 盒输入差分为a 时存在输出差分b, 并且当S 盒输入差分为b 时存在输出差分a,则称差分对a 和b 为可逆差分对, 简记为a ↔b.

以下用α=(un−1un−2···u0) 表示RECTANGLE 型算法的轮状态或者状态差分, 其中ui为16 进制整数.

定义2 (循环差分特征) 设α = (un−1un−2···u0) →β = (vn−1vn−2···v0) 是某算法的一条单轮差分特征. 如果β 为α 的循环移位, 则称α →β 为一条单轮循环差分特征. 更一般的, 设δ = (δ0→δ1→···→δr) 是某算法的一条r 轮差分特征, 如果δr为δ0的循环移位, 则称δ 为一条r 轮循环差分特征.

类似地, 可以定义可逆线性对和循环线性特征.

下面以RECTANGLE 算法为例说明如何构造单轮循环差分特征. 通过分析S 盒的差分分布表, 可得其存在可逆差分对(0010) ↔(0110), 其中(0010) →(0110) 的差分概率为2−3, (0110) →(0010)的差分概率为2−2. 基于这个可逆差分对, 如下构造一条单轮循环差分特征(0200 0060 0000 0000) →(2000 0600 0000 0000), 其中输入差分(0200 0060 0000 0000) 经过S 盒和行移位操作的状态差分比特表示如下:

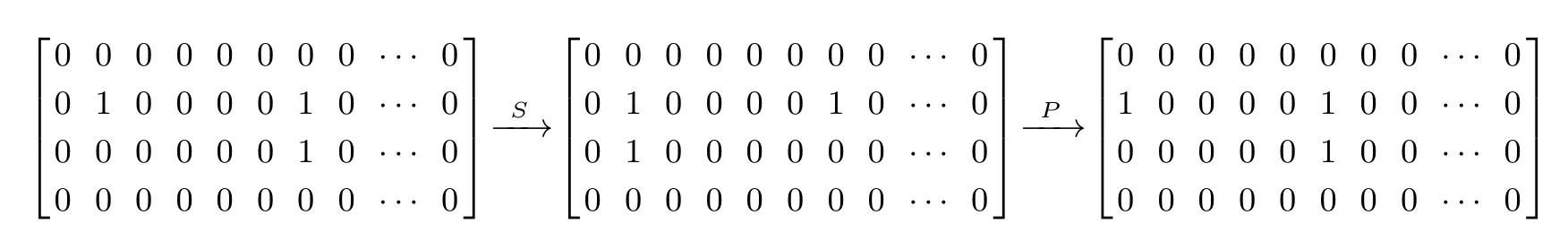
其中S 表示S 盒变换, P 是行移位变换. 注意到RECTANGLE 第二行第三行的循环左移位比特数分别为1 和12, 当第14 和第9 个S 盒的输入差分分别为2 和6, 输出差分分别为6 和2 时, 经行循环移位后, 第二行的第14 和第9 位的两个1 差分移到第15 和第10 位, 第三行的第14 位的1 差分移到了第10位, 故单轮变换后恰好第15 和第10 个S 盒的输出差分非零, 且差分样式与S 盒输入差分一样, 由此得到一条单轮循环差分特征(0200 0060 0000 0000)→(2000 0600 0000 0000), 重复上面的过程还可以构造其它循环差分特征.

更一般的, 考虑形如RECTANGLE 的扩散层为行循环移位的比特切片型算法. 假设算法有n 个4比特的S 盒, 依次为Sn−1Sn−2···S0, 且行移位量分别为lj, 0 ≤j ≤3. 对于这类算法, 定理1 给出了一个存在单轮循环差分特征的充分条件.

定理1 对于形如RECTANGLE 的扩散层为行循环移位的比特切片型算法, 如果其S 盒存在可逆差分对a ↔b, 并且该可逆差分对满足wt(a)≤2, wt(b)≤2 且wt(a ⊕b)=1, 则其存在单轮循环差分特征.

证明: 由条件知, a 和b 的重量一个为1, 一个为2, 且有一个非零比特位置相同. 不妨设wt(a)=1,wt(b)=2. 其中ap=bp=1, bq=1, 0 ≤p ≤3, 0 ≤q ≤3 且p=q.

类似于RECTANGLE 算法的分析, 我们选择输入差分使得其恰有两个活动S 盒, 两个活动S 盒的输入差分为(a,b), 输出差分为(b,a). 为保证经过行移位变换后仍然含有两个活动S 盒, 活动S 盒相差(lp−lq)mod n 个位置.

不妨设第i 个S 盒为活动S 盒, 其输入差分为a, 第j =(i+lq−lp)mod n 个S 盒为活动S 盒, 其输入差分为b, 而其它S 盒的输入差分都为0. 由于a ↔b 是可逆差分对, 我们取第i 个和j 个活动S 盒的输出差分分别为b 和a. 由于S 盒第p 个比特和第q 个比特的行移位参数分别是lp和lq, 于是经过P层后, 第p 行的第i, j 位的两个1 差分移到第(i+lp)mod n 和(j+lp)=(i+lq)mod n 位, 第q 行的第i 位的1 差分移到了第(i+lq)mod n 位, 因此输出差分仍只有两个活动S 盒, 分别为第(i+lp)mod n和第(i+lq)mod n 个S 盒, 且其输入差分分别为a 和b. 由此我们构造了一条单轮循环差分特征.

根据上面的分析, 单轮输出差分仍然恰有两个活动S 盒, 其输出差分仍然是a 和b, 且活动S 盒仍然相差(lp−lq)mod n 个位置, 因此上面的过程可以一直继续下去, 得到多条循环差分特征.

上面介绍的RECTANGLE 算法的例子中, 选择的两个活动S 盒恰好相差(12 −1)mod 16 = 11 个位置, 活动S 盒的输入差分分别为2 和6, 也满足定理1 的条件, 可以按定理中的方法构造各条循环差分特征. 对于线性特征, 如果其S 盒存在可逆线性对a ↔b, 并且可逆线性对满足wt(a) = 1, wt(b) = 2 且wt(a ⊕b)=1, 类似可以按定理1 构造循环线性特征.

4 长轮数差分和线性特征的构造

近年来自动化搜索手段被广泛应用于分析各类密码算法的安全性, 在差分和线性分析方面, 孙思维等人[12,13]提出了基于比特的MILP 自动化搜索模型, 用于求解最小活动S 盒个数及最优差分(线性) 特征. 然而, 随着算法分组长度的增加, 以及所需求解轮数的增大, 受限于计算资源, 利用自动化工具在有限时间内求解到一条或者多条最佳特征是困难的.

针对RECTANGLE 型扩散层为行循环移位的SPN 型算法, 利用上一节介绍的方法可以根据S 盒的差分和线性分布表, 快速构造出单轮循环差分或线性特征, 继而构造出多轮迭代循环差分或者线性特征.为了构造差分概率或者线性偏差更大的差分或者线性特征, 我们可以选择适当长轮数的迭代循环特征并借助MILP 方法搜索该迭代循环特征向前后扩展时具有给定输出或输入的更优的差分或线性特征. 对于64,128, 256 比特三种分组长度的SPN 型算法, 利用MILP 方法, 我们可以在有效时间内求解直到10 轮最优差分(线性) 特征. 更一般的, 我们还可以利用MILP 方法搜索低轮数的循环差分(线性) 特征, 并从这些低轮循环特征和迭代单轮循环特征中选择更优的扩展构造高轮数的差分(线性) 特征, 得到的主要结论如下.

4.1 RECTANGLE 算法的差分特征和线性特征

同第3 节快速构造单轮循环差分特征的方法, 分析RECTANGLE 算法S 盒的差分分布表发现, 存在满足定理1 条件的可逆差分对(0010) ↔(0110), 其中(0010) →(0110) 的差分概率为2−3, (0110) →(0010) 的差分概率为2−2. 因此, 可以按照定理1 的方法构造RECTANGLE 算法的单轮循环差分特征,其中第i 个S 盒Si和第j 个S 盒Sj为活动S 盒, j =(i+12 −1)mod 16, 两个活动S 盒的输入差分分别为(0010) 和(0110), 这条单轮循环差分特征相应的差分概率为2−5.

先利用MILP 方法建立搜索多轮最佳差分特征的模型, 得到低轮数的最优差分特征及概率作为参考依据. 遍历活动S 盒Si所有可能的位置, 构造出若干条单轮循环差分特征. 选取合适的迭代循环差分特征, 并利用MILP 方法向前后扩展搜索具有给定输入或输出差分的低轮最优差分特征, 由这些低轮差分特征拼接出长轮数的差分特征. 特别的, 对于RECTANGLE 算法, 基于一条7 轮的迭代单轮循环差分特征,在其前面添加1 轮, 并在其后面添加6 轮, 我们得到了一条差分概率为2−61的14 轮差分特征, 具体见表3, 该特征与现有的RECTANGLE 算法最佳差分特征的轮数及概率相同[4].

类似地, 分析RECTANGLE 算法的线性逼近表, 我们发现存在满足条件的可逆线性对(1000) ↔(1001), 其中(1000)→(1001) 线性特征的线性相关度为2−1, (1001)→(1000) 线性特征的线性相关度为2−2. 因此, 可以类似构造RECTANGLE 算法的单轮循环线性特征, 其中第i 个S 盒Si和第j 个S 盒Sj为活动S 盒, j =(i −13)mod 16, 两个活动S 盒的输入线性掩码分别为(1000) 和(1001), 相应的相关度为2−3. 我们从单轮循环线性特征(0080 0000 0000 0009)→(0090 0000 0000 0008) 出发, 迭代生成了7 轮循环线性特征, 并在其前面添加5 轮后面添加1 轮, 得到了RECTANGLE 算法的一条线性相关度为2−32的13 轮线性特征, 其具体中间状态的线性掩码值见表4.

表4 RECTANGLE 算法的13 轮线性特征Table 4 13-round linear characteristic of RECTANGLE

4.2 TANGRAM 算法的差分特征和线性特征

4.2.1 TANGRAM 128 算法差分特征的构造

对于TANGRAM 128 算法, 根据第3 节中快速构造单轮循环差分特征的方法, 分析TANGRAM 算法的差分分布表发现, 存在满足定理1 条件的可逆差分对(0010) →(0110), (1000) →(1100). 基于这两个可逆差分对, 对于TANGRAM 128 算法, 选择两个活动S 盒Si和Sj, 我们可以如下构造两类循环差分特征:

(1) 活动S 盒Si和Sj的输入差分分别是(0010) 和(0110), 输出差分分别是(0110) 和(0010), 其中j = (i+8 −1)mod 32, (0010) →(0110) 和(0110) →(0010) 的差分概率均为2−3, 构造出的单轮循环差分特征的概率为2−6.

(2) 活动S 盒Si和Sj的输入差分分别是(1000) 和(1100), 输出差分分别是(1100) 和(1000), 其中j =(i+8 −11)mod 32, (1000)→(1100) 和(1100)→(1000) 的差分概率均为2−3, 构造出的单轮循环差分特征的概率为2−6.

遍历上述两类单轮循环差分特征中活动S 盒Si的位置, 我们一共可以得到64 种单轮循环差分特征.

通过MILP 方法建模并求解TANGRAM 128 算法的低轮最优差分特征和概率. 以前面得到的64种单轮循环差分特征为基础迭代生成多轮循环差分特征, 并向前后扩展生成高轮数的差分特征, 选择其中的最优差分特征输出. 我们从单轮循环差分特征(0000 0000 0000 0000 0000 0000 6000 0002) →(0000 0000 0000 0000 0000 0000 2000 0006) 出发, 迭代生成了13 轮循环差分特征, 在该迭代循环差分特征前面添加4 轮, 后面添加6 轮, 得到了TANGRAM 128 算法的一条差分概率为2−128的23 轮差分特征, 其中间状态的具体差分值见表5.

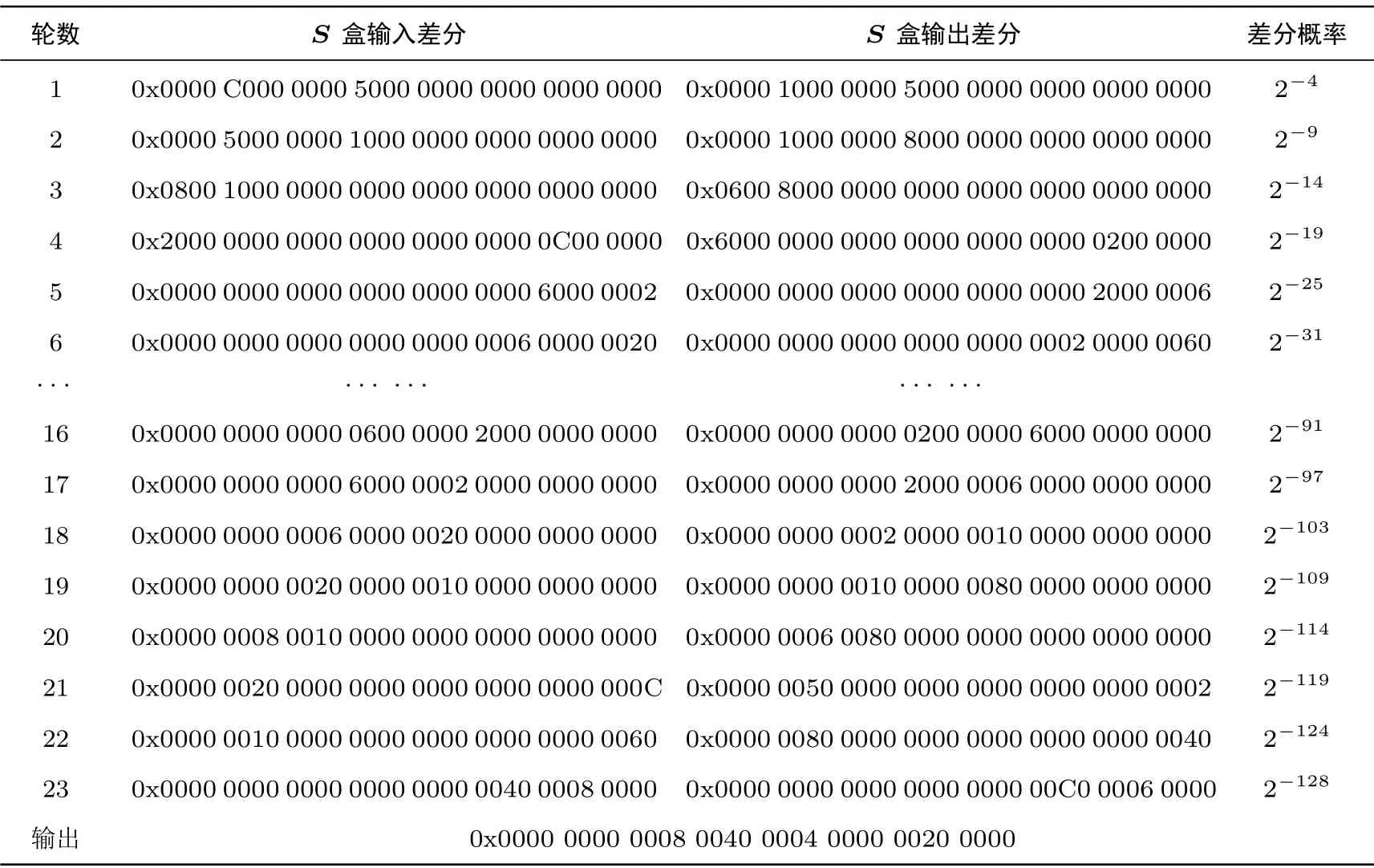
表5 TANGRAM 128 算法的23 轮差分特征Table 5 23-round differential characteristic of TANGRAM 128

由于上述方法构造出的差分特征的概率较低, 我们考虑基于更高概率的低轮循环差分特征扩展构造长轮数的差分特征. 利用MILP 方法我们搜索找到了TANGRAM 128 算法的3 条3 轮循环差分特征, 参见附录中的表8. 我们以3 轮循环差分特征(0000 0000 0000 0000 8001 0000 0000 0000) →(0000 0000 0000 0000 0001 0000 0008 0000) 为基础, 迭代6 次, 得到一条18 轮差分特征, 在该差分特征前面添加2 轮, 后面添加4 轮可以得到如表6 所示的概率为2−124的24 轮差分特征, 该特征的概率与作者设计文档中找到的最优24 轮差分特征的概率一样.

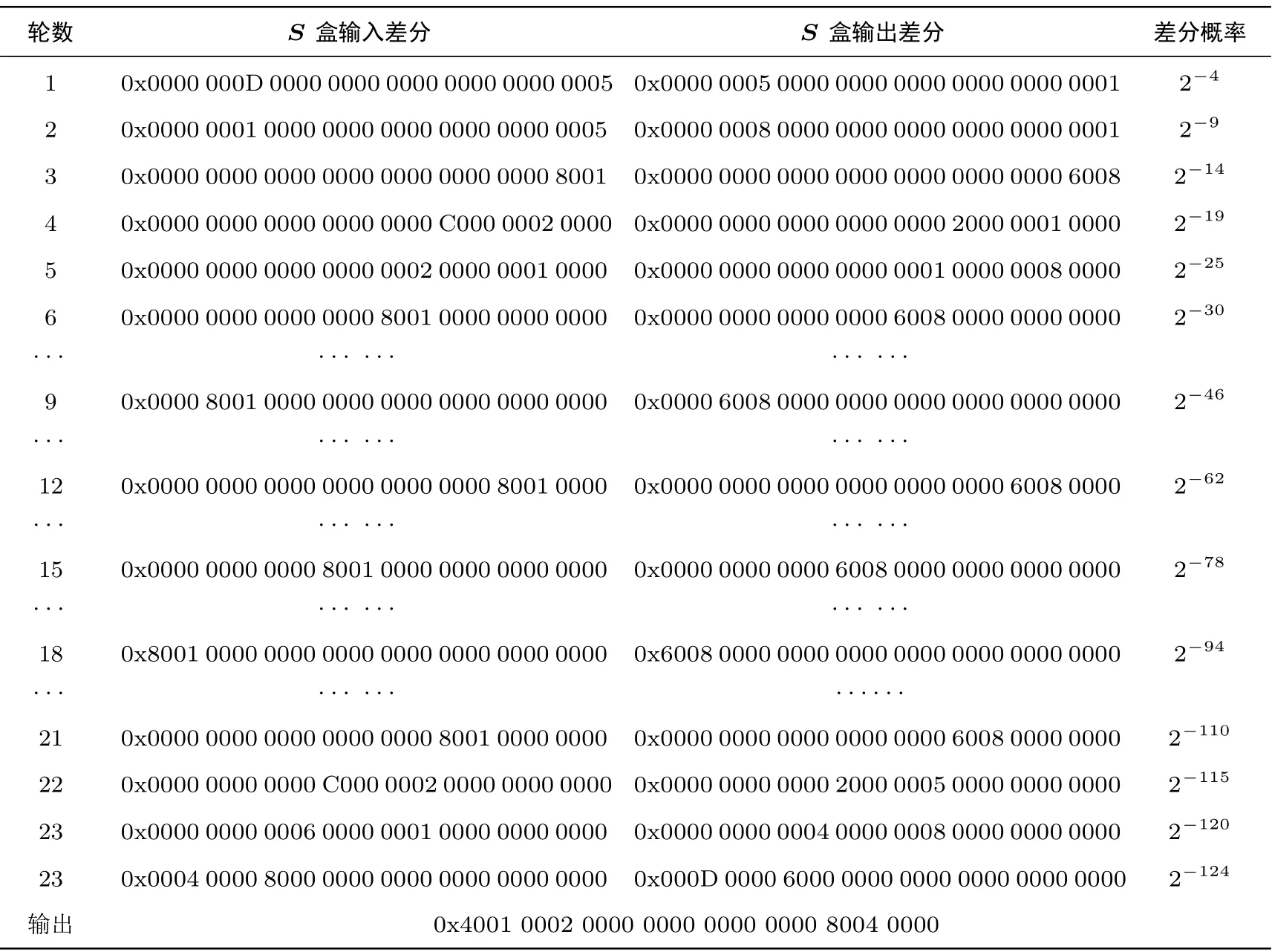
表6 TANGRAM 128 算法的24 轮差分特征Table 6 24-round differential characteristic of TANGRAM 128

4.2.2 TANGRAM 128 算法线性特征的构造

类似地, 分析TANGRAM 算法的线性逼近表, 我们发现其存在满足条件的可逆线性对(0001) →(0011) 和(0001)→(1001). 基于这两个可逆线性对, 对于TANGRAM 128 算法, 选择两个活动S 盒Si和Sj, 我们可以构造以下两类单轮循环线性特征:

(1) 活动S 盒Si和Sj的输入线性掩码分别为(0001) 和(0011), 输出线性掩码分别为(0011) 和(0001), 其中j =(i+1)mod 32, (0001)→(0011) 线性特征相关度为2−2, (0011)→(0001) 线性特征相关度为2−1, 构造出的单轮循环线性特征的线性相关度为2−3.

(2) 活动S 盒Si和Sj的输入线性掩码分别为(0001) 和(1001), 输出线性掩码分别为(1001) 和(0001), 其中j = (i+11)mod 32, (0001) →(1001) 线性特征相关度为2−1, (1001) →(0001)线性特征相关度为2−2, 构造出的单轮循环线性特征的线性相关度为2−3.

遍历上述两类单轮循环线性特征中活动S 盒Si的位置, 我们一共可以得到64 种单轮循环线性特征.

通过MILP 方法建模并求解TANGRAM 128 算法的低轮最优线性特征和相关度. 以前面得到的64 种单轮循环线性特征为基础迭代生成多轮循环线性特征, 并向前后扩展生成高轮数的线性特征, 选择其中的最优线性特征输出. 我们从单轮循环线性特征(0000 0000 0000 0009 0000 0000 0010 0000) →(0000 0000 0000 0001 0000 0000 0090 0000) 出发, 迭代生成了17 轮循环线性特征, 在该迭代循环线性特征前面添加5 轮后面添加1 轮, 我们得到了TANGRAM 128 算法的一条线性相关度为2−62的23 轮线性特征, 其中间状态的具体线性掩码见表7, 该特征的相关度与作者设计文档中找到的最优23 轮线性特征的相关度一样.

表7 TANGRAM 128 算法的23 轮线性特征Table 7 23-round linear characteristic of TANGRAM 128

4.2.3 TANGRAM 256 算法差分特征的构造

TANGRAM 256 算法和TANGRAM 128 算法采用相同的S 盒, 因此存在和TANGRAM 128 算法相同的可逆差分对和可逆线性对. 由于TANGRAM 256 算法和TANGRAM 128 算法的行移位参数不同, TANGRAM 256 算法的单轮循环特征不同点在于两个活动S 盒的间距与TANGRAM 128 不同. 具体地, TANGRAM 256 算法存在如下两类单轮循环差分特征:

(1) 活动S 盒Si和Sj的输入差分分别是(0010) 和(0110), 输出差分分别是(0110) 和(0010), 其中j =(i+8 −1)mod 64, 单轮循环差分特征的概率为2−6.

(2) 活动S 盒Si和Sj输入差分分别为(1000) 和(1100), 输出差分分别是(1100) 和(1000), 其中j =(i+8 −41)mod 64, 单轮循环差分特征的概率为2−6.

遍历上述两类单轮循环差分特征中Si的位置, 一共可以得到128 种单轮循环线性特征.

我们从单轮循环差分特征(0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 6000 0002) →(0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 2000 0006)出发, 迭代生成了34 轮循环差分特征, 在该迭代循环差分特征前面添加4 轮, 后面添加6 轮, 我们得到了TANGRAM 256 算法的44 轮差分特征, 其差分概率为2−254, 中间状态的具体差分值见附录中表9.

由于上述方法构造出的差分特征的概率较低, 我们考虑基于更高概率的低轮循环差分特征扩展构造长轮数的差分特征. 利用MILP 方法我们搜索找到了TANGRAM 256 算法的3 条3 轮循环差分特征, 其概率均为2−16, 参见附录中的表10. 我们以3 轮循环差分特征(0000 0000 0000 0000 0100 0000 0000 0000 0000 0000 0000 0000 8000 0000 0000) →(0000 0000 0000 0000 0000 0000 0000 0000 0000 0001 0000 0008 0000 0000 0000 0000) 为基础, 迭代14 次, 得到一条42 轮差分特征, 在该差分特征前面添加2 轮, 后面添加4 轮可以得到附录中的表11 所示的概率为2−252的48 轮差分特征, 该特征与作者设计文档中找到的48 轮最优差分特征的概率一致.

4.2.4 TANGRAM 256 算法线性特征的构造

TANGRAM 256 算法和TANGRAM 128 算法采用相同的S 盒, 因此存在和TANGRAM 128 算法相同的可逆线性对, 利用这两个可逆线性对, 可以构造如下两类单轮循环线性特征:

(1) 活动S 盒Si和Sj输入线性掩码分别为(0001) 和(0011), 输出掩码分别为(0011) 和(0001),其中j =(i+1)mod 64, 单轮线性相关度为2−3.

(2) 活动S 盒Si和Sj输入线性掩码分别为(0001) 和(1001), 输出掩码分别为(1001) 和(0001),其中j =(i+41)mod 64, 单轮线性相关度为2−3.

遍历上述两类单轮循环线性特征中Si的位置, 一共可得到128 条单轮循环线性特征.

与TANGRAM 128 算法线性特征的构造相似, 对于TANGRAM 256 算法, 我们从单轮循环线性特征(0000 0000 0000 0000 0000 0090 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001) →(0000 0000 0000 0000 0000 0090 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001) 出发, 迭代生成了38 轮循环线性特征, 在该迭代循环线性特征前面添加5 轮, 后面添加1 轮, 我们得到了TANGRAM 256 算法的44 轮线性特征, 其线性相关度为2−125, 中间状态的具体线性掩码见附录中表12. 需要说明的是, 作者的设计文档中只给出了直到29 轮最优线性特征的相关度, 而利用MILP 方法我们也难以在有效时间内直接寻找44 轮线性特征. 本文利用循环线性特征方便地构造了TANGRAM 256 算法的长轮数的线性特征.

另外, 利用MILP 方法我们搜索找到了TANGRAM 256 算法的1 条2 轮循环线性特征和2 条4 轮循环线性特征, 但其较单轮循环特征的线性相关度并没有提高, 因此不采用多轮循环线性特征进行构造.

5 结束语

本文对于采用比特切片思想设计的RECTANGLE 等算法进行了结构性分析, 根据行移位量和S 盒的差分及线性分布之间的关系, 提出了快速构造单轮循环特征的方法. 进一步, 扩展单轮循环特征的思想,利用MILP 自动化搜索方法搜索了低轮数的循环特征, 再由这些单轮循环特征或者低轮循环特征迭代生成较长轮数的特征, 并向前后扩展构造更长轮数的差分和线性特征. 应用于RECTANGLE、TANGRAM 128 和TANGRAM 256 算法, 分别给出差分和线性特征. 针对分组规模较大的SPN 型算法, 我们的方法可以根据算法组件特点判断并构造长轮数特征, 具有明显的实用价值. 然而我们的构造方法在很大程度依赖于算法S 盒的设计, 无法保证求解所得到的特征是否为最优解, 如何利用MILP 方法快速求解最优解仍是我们下个阶段重要的研究工作.