医疗辅助诊断系统中新型的双向隐私保护方法*

陈磊磊, 陈兰香, 穆 怡,2

1. 福建师范大学 数学与信息学院福建省网络安全与密码技术重点实验室, 福州350117

2. 澳门城市大学 数据科学研究院, 澳门

1 引言

传统的医疗诊断是医生通过整理与分析一组临床数据(包括症状、实验检查等) 进行诊断, 依靠的是医生的知识基础、个人洞察力以及对可用信息的整理与分析的能力. 其诊断准确率完全依赖医生的判断,即使是经验丰富的医生也可能因为自身原因而做出错误的分析及判断, 因此可能导致诊断结果出错的几率较大.

近些年, 机器学习技术取得长足的发展与进步, 利用机器学习的医疗辅助诊断系统(Medically Assisted Diagnosis Systems, MADS) 也得到极大的关注与发展. MADS 可以实现对疾病的全面分析, 帮助临床医生更好地进行诊断, 可以极大地降低误诊和漏诊的概率. 同时, 确诊的数据可以及时地添加到数据库, 有助于构建更加有效的决策树. 此外, 系统的自我更新功能可以更好地适应医学信息的爆炸式增长.

然而, 医疗信息化技术在改善医疗诊治水平的同时, 也导致患者隐私泄露、数据丢失、业务中断等安全威胁. 现有的医疗辅助诊断系统大都注重诊断的准确性而忽视了隐私保护的重要性. 因此, 为了保护医疗辅助诊断系统中患者的个人隐私, 本文提出一种新的结合决策树与OT 技术的双向隐私保护模型. 该模型在用户进行医疗数据查询并得到准确查询结果的情况下, 能够极好地保护用户、服务器以及数据库的隐私信息.

本文提出的医疗辅助诊断系统的隐私保护方法分为两个阶段: 决策树构建与查询阶段. 在决策树构建阶段, 针对数据库的来源不同对医疗辅助诊断系统进行分类, 分为服务器自身拥有数据库的MADS 和数据来源于第三方的MADS. 针对服务器自身拥有数据库的MADS, 可以采用典型的决策树算法构建决策树. 针对数据来源于第三方的MADS 采用熊等人[1]提出的用于构建决策树的差分隐私保护数据发布算法(DT-Diff) 进行决策树的构建, 确保在构建决策树的过程中不会泄露数据库的隐私, 本文将重点介绍这一类方案. 构建决策树不仅有助于提高诊断的准确性, 也有助于提高方案的查询效率.

查询阶段包括建立索引协议和OT 协议两个方面. 为了将决策树算法与OT 协议有效结合, 我们提出一种决策树索引协议, 可以高效地将决策树信息数字化, 从而便于利用OT 协议保护双向隐私. 客户端和服务器通过该索引协议对各自的数据建立索引, 从而为数据查询做好铺垫. OT 协议不仅保护客户端的隐私, 同时也可以保证客户端只能获得查询的相关信息, 而不能获得其它额外信息, 从而保护服务器的隐私.理论分析表明, 本文提出的方法不仅保护了数据库的隐私也保护了客户端和服务器的隐私, 并且具有较高的通信效率. 实验结果也表明, 此模型不仅具有较高的查询效率还具有较高的查询准确率.

以下章节安排如下: 第2 节介绍医疗辅助诊断系统的相关研究工作, 指出本研究工作与之前研究工作的不同. 第3 节介绍系统模型及其相关的基础知识. 第4 节详细介绍本文提出的方法在MADS 系统中的应用设计与实现. 第5 节对该方法在MADS 系统中的应用进行安全性分析与性能评估, 最后对本文进行总结并介绍下一步的工作.

2 相关工作

当今信息化时代, 利用大数据可以更好地改善人们的生活. 在健康医疗领域, 随着医院信息化建设的不断发展, 医院数据库中的信息呈爆炸式增长, 而医疗数据对于疾病的诊断、控制和各种医疗研究具有重要的价值. 机器学习利用计算机模拟人类的学习行为, 通过建模来对已有的数据进行分析处理来获取新经验与新知识, 不断改善性能并实现自身完善.

机器学习已在健康医疗领域得到广泛应用. 如Castro-Zunti 等人[2]首次使用基于统计机器学习和深度学习的分类器, 通过对计算机断层扫描(Computed Tomography, CT) 图像分析, 结合患者的年龄来检测早期强直性脊柱炎(Ankylosing Spondylitis, AS) 症状的侵蚀. 实验结果显示随机森林分类器的性能优于kNN 分类器, 并且在不减少验证损失的情况下进行训练的深度学习分类器是最佳的. Alabi 等人[3]比较了四种预测口舌鳞状细胞癌(Oral Tongue Squamous Cell Carcinoma, OTSCC) 患者局部复发风险的机器学习算法的性能, 这些算法分别是支持向量机(Support Vector Machine, SVM)、朴素贝叶斯(Naive Bayes, NB)、增强决策树(Boosted Decision Tree, BDT) 和决策森林(Decision Forest, DF).实验结果表明, 改进后的决策树算法能获得最佳的分类精度. 此外应用增强决策树机器学习算法可以对OTSCC 患者进行分层, 从而帮助其制定个性化的治疗计划. Liu 等人[4]在分类前采用随机森林回归的方法来填充缺失值, 并将基于深度神经网络(Deep Neural Network, DNN) 的自动超参数优化(Automated Hyperparameter Optimization, AutoHPO) 应用于不平衡数据集的笔画预测, 为基于不完整和等级不平衡的生理数据开发一种混合机器学习方法来预测脑卒中的临床诊断. 结果表明该方法有效地降低了假阴性率, 总体准确率较高, 成功地降低了卒中预测的误诊率. Tseng 等人[5]使用机器学习算法, 即随机森林、支持向量机、逻辑回归和贝叶斯分类算法, 根据肿瘤细胞的表面标记物和血清试验来预测乳腺癌. 实验结果显示, 他们提出的基于随机森林的模型被认为是至少提前3 个月预测乳腺癌转移的最佳模型, 有利于早发现乳腺癌复发及尽早治疗.

为了更加高效地利用已有的医疗知识, 在健康医疗诊断中, 人们通常使用决策树对医疗大数据进行分析从而对患者的发病类型及概率进行有效地预测.

如Ting 等人[6]通过基于专家经验的特征提取技术与决策树算法的自动特征选择能力相结合,开发了一个预测中度到重度阻塞性睡眠呼吸暂停(Obstructive Sleep Apnea, OSA) 综合症的诊断系统. 与多变量logistic 回归模型和其他四种决策树算法进行比较,结果显示,所提出的最佳预测公式在灵敏度为98.2%和特异性为93.2% 的总体准确度达到96.9%. Yu 等人[7]使用思维导图和迭代决策树(Iterative Decision Tree, IDT) 方法来整合临床实践指南, 开发一个治疗甲状腺结节的临床决策支持系统(Clinical Decision Support System, CDSS). 实验数据显示, CDSS 建议与常规临床治疗的一致性为78.9%. Kolluru 等人[8]开发了一种使用决策树对血管内光学相干断层扫描图像中体素斑块类型进行分类的方法. 此方法利用受物理启发的光学特征、强度特征和纹理特征来区分不同的菌斑类型, 并将体素分为四类, 即纤维化型、钙化型、富脂型和其他型. 实验结果显示, 在训练集的所有褶皱和所有斑块类型上取得了92% 的良好准确率. 以上研究工作说明决策树分类算法在医疗辅助诊断中具有极高的应用价值, 但是这些工作只考虑了模型的准确率而忽视了数据的隐私保护.

健康医疗数据是高敏感数据, 隐私泄露会对患者造成极大的伤害. 为了保护患者数据隐私, 2018 年,Zhang 等人[9]提出了一种新颖的身份验证和密钥协商机制, 该机制通过协商共享密钥来加密/解密敏感信息从而保护通信过程中的隐私数据. 该方案利用混沌地图实现相互认证和密钥约束, 并利用动态身份来实现用户的匿名性和对高度隐私要求的护理点的用户不可追溯性. 2019 年, Lee[10]提出一种自适应可逆水印算法, 可直接应用于保留医学图像质量的医疗系统以保护医疗记录. 2020 年, Zhu 等人[11]利用人脸交换技术, 使得患者的脸部可能会交换为适当的目标脸部而变得无法识别, 从而达到保护医疗视频中的患者隐私的目的.

与以上方案不同, 本文首次提出结合决策树与不经意传输技术实现医疗辅助诊断系统的双向隐私保护. 提出的方法利用决策树对已有诊断信息进行分类来形成辅助诊断, 为了实现查询过程中的双向隐私保护, 首先利用差分隐私对决策树加入噪声从而确保决策树构建过程中不会泄露数据库的隐私. 为了将决策树算法与OT 协议有效结合, 我们提出一种决策树索引协议, 可以高效地将决策树信息数字化, 从而便于利用OT 协议保护客户端的隐私, 同时也可以保证客户端只能获得查询的相关信息, 而不能获得其它额外信息, 从而保护服务器的隐私. 提出的方法最早将决策树与OT 技术应用于医疗辅助诊断系统.

3 基础知识

3.1 符号定义

本文采用的符号如下所示.

3.2 系统模型

本文提出的支持双向隐私保护的医疗辅助诊断系统包括三个实体, 即数据提供者、客户端和服务器,其中客户端是用户查询的入口, 服务器为用户提供查询服务, 其系统模型如图1 所示. 双向隐私保护指同时保护客户端和服务器的隐私, 同时为了保护数据提供者的数据隐私, 我们利用文献[1] 提出的用于构建决策树的差分隐私保护数据发布算法DT-Diff 进行决策树的构建, 确保在构建决策树的过程中不会泄露数据库的隐私. 为了保护客户端和服务器的隐私, 我们利用文献[12] 提出的针对恶意接收者的OT 协议确保查询时客户端和服务器的隐私. OT 协议使得客户端只能得到发送的查询请求对应的查询结果, 而不能得到其他任何信息, 从而保护服务器的隐私; 同时, OT 协议可以保证服务器不知道客户端查询的信息,从而确保客户端的隐私.

提出的医疗辅助诊断系统双向隐私保护方法主要包括两个阶段. (1) 决策树构建阶段: 为了保护数据提供者的数据隐私, 对数据执行隐私保护算法. 与DT-Diff 算法略有不同的是, 本文将此算法分为两个部分来执行. 第一步, 数据提供者首先对数据库中的数据进行完全泛化, 然后通过循环迭代对数据进行逐步细分以得到所有细分方案s, 并计算每种细分方案的可用性水平u(D,s), 此后, 数据提供者将得到的所有细分方案及其对应的被选择概率发送给服务器. 第二步, 服务器采用随机函数, 根据方案被选择概率在所有细分方案中选择一种细分方案构建决策树. (2) 查询阶段: 客户端发送查询请求给服务器, 服务器根据设计的OT 算法协议将计算结果返回给客户端, 客户端通过OT 协议计算得到查询结果.

图1 系统模型Figure 1 System model

本文设计的OT 协议可以保证服务器不能得到客户端的计算结果, 客户端也只能得到查询相关的信息, 而得不到其它额外信息, 从而可以实现双向隐私保护. 为了将DT-Diff 算法和OT 协议有效结合, 我们提出决策树索引协议, 可以高效地将决策树信息数字化. 决策树索引由服务器构建并发布, 客户端能够采用同样的索引协议将查询请求信息数字化, 从而利用OT 协议实现隐私保护.

3.3 差分隐私

3.3.1 定义

差分隐私[13]是Dwork 在2006 年针对统计数据库的隐私泄露问题提出的一种新的隐私定义. 在此定义下, 单个记录的变化对数据集处理结果的影响几乎是微乎其微的.

定义1 (差分隐私) 对于任意两个邻近数据集D1和D2, 数据间最多相差一条记录, 给定一个隐私保护算法A, range(A) 表示算法A 所有可能输出构成的集合, 对于range(A) 的任意子集S, 若算法A 满足公式(1),

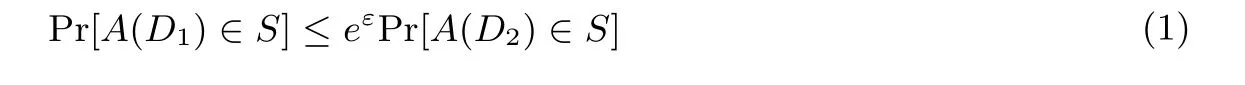
则称算法A 提供ε-差分隐私保护. 其中Pr[Es] 表示事件Es发生的概率, 即隐私泄露的风险. 参数ε 称为隐私保护预算[14], 即由数据拥有者视数据安全需求所指定的隐私保护水平.

3.3.2 实现机制

为了使一个随机化算法具有ε-差分隐私性, 文献[15] 提出了实现差分隐私保护的Laplace 机制.Laplace 机制通过向确切的查询结果中加入服从Laplace 分布的随机噪声来实现ε-差分隐私保护. 记位置参数为0、尺度参数为b 的Laplace 分布为Lap(b), 那么其概率密度函数为公式(2).

定义2 (Laplace 机制) 给定数据集D, 设有函数f :D →Rd(表示d 维实数向量), 其敏感度为∆f,那么随机算法A(D) = f(D)+Y 提供ε-差分隐私保护, 其中Y ∼Lap(∆f/ε) 为随机噪声, 服从尺度参数为∆f/ε 的Laplace 分布.

由于Laplace 机制仅适用于数值型数据, 而在实际应用中, 有大量的非数值型数据. 因此, McSherry等人[16]提出了指数机制.

定义3 (指数机制) 设算法A 的输入为数据库D, 输出为一实体对象r ∈range(A), range(A) 为算法A 的输出域, 函数q(D,r) →R 称为输出值r 的可用性度量函数, 用来评估输出值r 的优劣程度. 其中R 表示实数集, ∆q 是函数q 的敏感度. 若算法A 以正比于eεq(D,s)/2∆q的概率从range(A) 中选择并输出r, 那么算法A 提供ε-差分隐私保护.

此外, 还有其他的机制建立在这两个经典机制之上, 如基于数据划分与数据聚合[17–20]、基于适应性查询[21]的隐私保护机制. 其它隐私保护机制还有基于高斯分布[22]、基于相关性[23]、基于最优机制[24]以及基于变换编码[25]等.

3.4 OT 协议

3.4.1 定义

3.4.2 针对恶意用户的OT 协议

文献[12] 提出的OT 协议是一个OTnk协议, 即接收方同时选择k 个消息. 文献[12] 考虑了半诚实的发送方和半诚实/恶意的接收方, 而本文考虑的是恶意接收方的情况, 即在医疗辅助诊断系统中客户端可能是不诚实的甚至是恶意的. 针对恶意接收方的OTnk协议设计如算法1 所示, 其中发送方是服务器, 接收方是客户端.

在算法1 中, 接收方首先根据{σ1,σ2,··· ,σk} 经过计算得到{A1,A2,··· ,Ak} 并发送给发送方,基于Diffie-Hellman 困难假设, 发送方不可能通过{A1,A2,··· ,Ak} 得到{σ1,σ2,··· ,σk}, 因此接收方的信息是无条件安全的. 在收到接收方发送的{A1,A2,··· ,Ak}, 发送方计算y、{D1,D2,··· ,Dk}以及 {c1,c2,··· ,cn} 并发送给接收方. 接收方根据发送方传来的参数计算出 Kj, 进一步得到{σ1,σ2,··· ,σk} 对应的{mσ1,mσ2,··· ,mσk}. 在此过程中接收方只得到发送方的y、{D1,D2,··· ,Dk}以及{c1,c2,··· ,cn}, 因为接收方只输入了{σ1,σ2,··· ,σk}, 因此接收方不会得到其它额外的信息. 综上所述, 算法1 既保护了接收方的隐私, 也保护了发送方的隐私, 因为接收方在查询过程中只得到了与其查询相关的信息, 而不能获得其它任何额外的信息.

算法1 针对恶意接收方的OTnk 协议Input: (g,H1,H2,Gq), 其中Gq 是Z∗p 的子群, 其阶为q, g 是Gq 的一个生成子群, H1, H2 为哈希函数. 发送方的数据{m1,m2,··· ,mn}, 接收方的选择{σ1,σ2,··· ,σk}.Output: mσ1,mσ2,··· ,mσk.1 接收方计算wσj = H1(σj) 和Aj = wσj gaj , 其中aj ∈R Z∗p, j = 1,2,··· ,k;2 接收方将A1,A2,··· ,Ak 发送给发送方;3 发送方计算y = gx, Dj = (Aj)x, wi = H1(i), ci = mi ⊕H2(wxi), 其中x ∈R Z∗p, i = 1,2,··· ,n,j = 1,2,··· ,k;4 发送方将y、D1,D2,··· ,Dk 和c1,c2,··· ,cn 发送给接收方;5 接收方计算Kj = Dj/yaj, 得到mσj = cσj ⊕H2(Kj).

其正确性推导见公式(3).

4 新型的双向隐私保护方法

为了实现医疗辅助诊断系统中的双向隐私保护, 首先利用决策树对已有诊断信息进行分类来形成辅助诊断, 为了实现查询过程中的双向隐私保护, 首先利用差分隐私对决策树加入噪声从而确保决策树构建过程中不会泄露数据库的隐私. 无论是决策树还是OT 协议, 在系统中都不能直接应用, 为了将决策树算法与OT 协议有效结合, 我们提出一种决策树索引协议, 可以高效地将决策树信息数字化, 从而在医疗辅助系统中应用设计的OT 协议实现客户端和服务器的双向隐私保护.

4.1 基于DT-Diff 算法的决策树构建

利用DT-Diff 算法来构建决策树的过程包括两个阶段: (1) 细分方案阶段, 数据提供者将数据库中的数据进行完全泛化后再细分, 并计算每种细分方案被选择的概率; (2) 决策树构建阶段, 服务器按照一定的概率分布选择一种细分方案构建决策树. 下面将对两个阶段进行详述.

4.1.1 细分方案划分

数据提供者首先对数据集进行完全泛化, 然后通过多次循环迭代完成数据的逐步细分, 每次迭代的主要任务是从全部属性值中以指数机制选择一个值进行细分, 并计算每种细分方案s 的可用性水平u(D,s).在用指数机制选择一个属性值进行细分时, 需要根据属性值的类型采用相应的细分方法. 对于离散属性的细分要依照事先设计的细分层次树, 对于连续属性的细分则是从其值域中选择分裂点来将其一分为二, 必须保证选择的分裂点在数据集中没有出现, 否则会违背差分隐私的要求. 数据的细分流程如图2 所示.

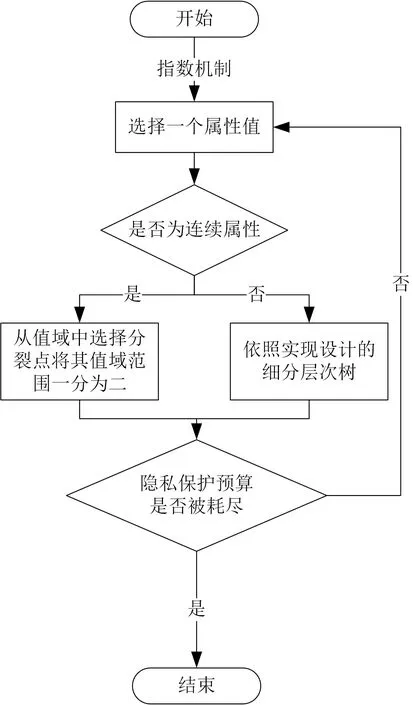
图2 数据细分Figure 2 Data subdivision

以计算生物学中的Acute Inflammations (急性炎症) 数据集[29]的部分属性为例, 如表1 所示.

表1 原始数据集Table 1 Original dataset

包括3 个症状属性, 其中离散属性Urination (表示排尿是否持续) 与Nausea (表示是否恶心) 的值域均为{Yes, No}, 连续属性TEMP (表示患者的体温) 的值域为[35.5, 41.5]. 类别属性有Urocystitis (表示是否患膀胱炎) 与Nephritis (表示是否患肾源性肾炎). 对该数据集的细分处理过程如图3 所示. 第一步是初始化, 然后进行三轮循环迭代就可以得到全部细分方案.

得到细分方案后, 需要计算每种细分方案s 的可用性水平u(D,s), 主要有两种方式[1]: 基于信息增益与基于最大频数和.

(1) 基于信息增益的可用性函数

图3 细分处理过程Figure 3 Subdivision process

基于信息增益的可用性函数见公式(4), 其中v 为属性Atrri的一个值, v1,··· ,vk为v 细分后的值,Dv表示Atrri=v 的元组构成的数据集, I(Dv) 为数据集Dv的熵, H(Dv) 是所有子集的熵的加权和.

数据集Dv的熵I(Dv) 的计算见公式(5), 其中t 是分类属性不同取值的种类数, 即t 个不同类Ci,属于类Ci的样本个数为ci, Pri=ci/|Dv|, |Dv| 表示Dv中元组的个数.

所有子集的熵的加权和H(Dv) 的计算见公式(6), 其中k 是v 细分后的值的个数, Dvj表示Atrri=vj的元组构成的数据集, I(Dvj) 是数据集Dvj的熵.

由文献[1] 知, 采用基于最大频数和的可用性函数的查询准确率高于采用基于信息增益的可用性函数,我们将在实验部分对采用不同可用性函数的查询准确率进行评估, 从而验证文献[1] 中针对可用性函数的实验结果.

细分方案的划分如算法2 所示, 其中solution 为所有的细分方案集S 的集合. 方案s 被选择的概率计算见公式(8).

其中E(D,s) = eεu(D,s)/2∆u, 表示方案s 以正比于eεu(D,s)/2∆u的概率参与全局选择. 针对连续属性值,设sz表示任一连续属性值细分方案集Sj中的一个方案, 其中z =1,2,··· ,|Sj|, |Sj| 表示细分方案集Sj中方案的数量. u(D,sz) 表示方案sz的可用性水平. 根据细分方案划分的基本原理, 方案sz在细分方案集Sj中以指数机制被选择的概率见公式(9).

连续属性值的细分方案sz以正比于P(sz)eεu(D,s)/2∆u的概率参与全局选择, 即针对连续属性值,E(D,sz) = P(sz)eεu(D,s)/2∆u. 针对离散属性或文本型属性的细分方案s, 则以正比eεu(D,s)/2∆u的概率参与全局选择. 即E(D,s)=eεu(D,s)/2∆u.

?

4.1.2 决策树构建

数据提供者将所有细分方案及其对应方案被选择的概率发送给服务器, 服务器根据方案被选择的概率, 使用随机函数按照一定的概率分布在所有细分方案中选择一种细分方案构建决策树. 细分方案选择如算法3 所示.

4.2 基于OT 协议的双向隐私保护

4.2.1 决策树索引协议

决策树是一种树形结构, 上述决策树的每个内部节点表示一个属性, 每个分支表示对属性取值的一个判断结果, 末端叶子节点表示根据属性判断得到的一种分类结果. 这种数据结构在OT 协议中是无法直接处理的, 为了使得上述决策树算法可应用在基于OT 的隐私保护协议中, 我们提出将决策树数字化的决策树索引协议.

决策树的数据属性及分类结果主要包括数值型数据与文本型数据, 为了将这些数据数字化, 采取的索引机制是: 对于连续型数值数据, 先将连续数据划分为区间, 然后对区间依次编号, 编号从0 开始, 编号值即为索引值; 而对于离散型数值数据和文本型数据, 则根据其值进行编号, 编号从0 开始, 编号值即为索引值.

根据医疗数据属性的作用, 可以将医疗数据的属性分为两类, 即症状属性与类别属性. 服务器构建决策树后, 创建并发布决策树索引协议, 索引协议包括属性排列和属性索引表两部分. 属性排列主要是对属性的先后顺序加以描述, 本节主要介绍属性索引表的建立, 以图3 的细分为例展开介绍.

(1) 对连续型数值数据的处理

患者的体温属性TEMP 为连续型数值数据, 其值域为[35.5, 41.5], 细分完成之后TEMP 被划分为[35.5, 38.2] 与(38.2,41.5] 两个区间, 可以认为属性TEMP 有两种取值, 因此建立如表2 的索引表.

(2) 对离散型数值数据和文本型数据的处理

属性Urination 表示患者排尿是否持续, 为文本型数据, 属性Urination 的值域为{yes, no}, 将yes的索引取为0, 将no 的索引取为1. 因此可以建立如表3 的索引表.

表2 TEMP 属性索引表Table 2 Index table of TEMP attribute

表3 Urination 属性索引表Table 3 Index table of Urination attribute

根据上述索引规则, 图3 对应的属性索引如表4 所示.

表4 属性索引表Table 4 Index table of attributes

为每个属性建立索引后, 服务器要对决策树的每个等价类进行处理, 即将决策树中每个等价类用二元组(症状对应的索引, 疾病索引) 表示, 仍然以图3 为例介绍具体过程.

令l 为症状属性的个数(图3 中l = 3), h 为决策树中除类别属性之外的其他属性值个数的最大值(图3 中h=2), 那么症状对应的索引可以表示为公式(10).

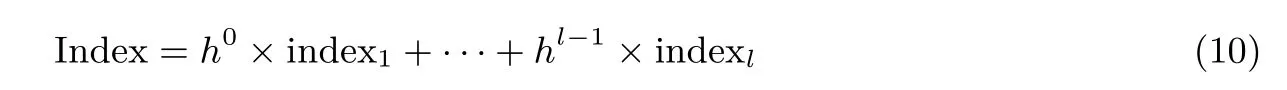
其中Index 表示症状对应的索引, indexi表示第i(1 ≤i ≤l) 个属性对应取值的索引.

按照以上公式对所有的类别属性使用相同的方法可以得出疾病的类型, 以类别属性Urocystitis 和Nephritis 为例, 其索引可以表示为公式(11).

由上式可以看出此疾病索引值有0、1、2 与3 四种. 其中0 表示Urocystitis = 0 ∩Nephritis = 0,1 表示Urocystitis = 1 ∩Nephritis = 0, 2 表示Urocystitis = 0 ∩Nephritis = 1, 3 表示Urocystitis =1 ∩Nephritis=1.

为了保证查询的准确性, 在对决策树建立索引之前需要将决策树补全, 即将症状属性所有可能的组合方式都展现在决策树上, 再对补全的决策树建立索引.

4.2.2 基于OT 的双向隐私保护协议

通过决策树索引协议将决策树数字化后, 就可以设计基于OT 协议的隐私保护协议保护查询过程中客户端和服务器的双向隐私. 本文设计的基于OTnk的双向隐私保护协议取k = 1, 双向隐私保护协议如算法4 所示, 其中客户端是接收方, 服务器是发送方.

算法4 基于OT 的双向隐私保护协议Input: (g,H1,H2,Gq), 其中Gq 是Z∗p 的子群, 其阶为q, g 是Gq 的一个生成子群, H1, H2 为哈希函数. 发送方的数据mIndex1,mIndex2,··· ,mIndexn, 其中mIndexi 表示服务器集合中第i(1 ≤i ≤n) 个症状索引对应的疾病索引, 接收方的选择IC.Output: mIC.1 接收方计算wIC = H1(IC) 和AIC = wICgaIC , 其中aIC ∈R Z∗p;2 接收方将AIC 发送给发送方;3 发送方计算y = gx, DIC = (AIC)x, wi = H1(Indexi), ci = mIndexi ⊕H2(wxi), 其中x ∈R Z∗p,i = 1,2,··· ,n;4 发送方将y、DIC 和c1,c2,··· ,cn 发送给接收方;5 接收方计算KIC = DIC/yaIC, 得到mIC = cIC ⊕H2(KIC).

在执行算法之前, 假设服务器已经构建好了决策树及其对应的索引, 客户端先将要查询的症状输入并得到症状对应的索引(其中症状有多个属性, 一个症状对应一条索引). 在算法4 中, 客户端首先使用索引IC 经过计算得到AIC并发送给服务器, 基于Diffie-Hellman 困难假设[12], 服务器不可能通过AIC得到IC, 因此客户端的信息是无条件安全的. 在收到客户端发送的AIC, 服务器计算y、DIC以及决策树对应的c1,c2,··· ,cn并发送给客户端. 客户端根据服务器传来的参数计算出KIC, 然后计算H2(KIC), 再在c1,c2,··· ,cn中查找与H2(KIC) 值相等的H2(wxi) 对应的i 值, 从而得出cIC, 进一步得到索引IC 对应的疾病类型mIC. 在此过程中客户端只得到服务器的y 和c1,c2,··· ,cn, 因为客户端只输入了索引IC, 因此客户端不会得到其它额外的信息.

以表1 的数据为例, 构建的决策树如图4(a) 所示, 为了保证查询结果的准确性, 在对决策树建立索引之前需要将决策树补全, 将图4(a) 的决策树补全后的决策树如图4(b) 所示. 症状属性的排列为TEMP、Urination 与Nausea, 类别属性的排列为Urocystitis 与Nephritis.

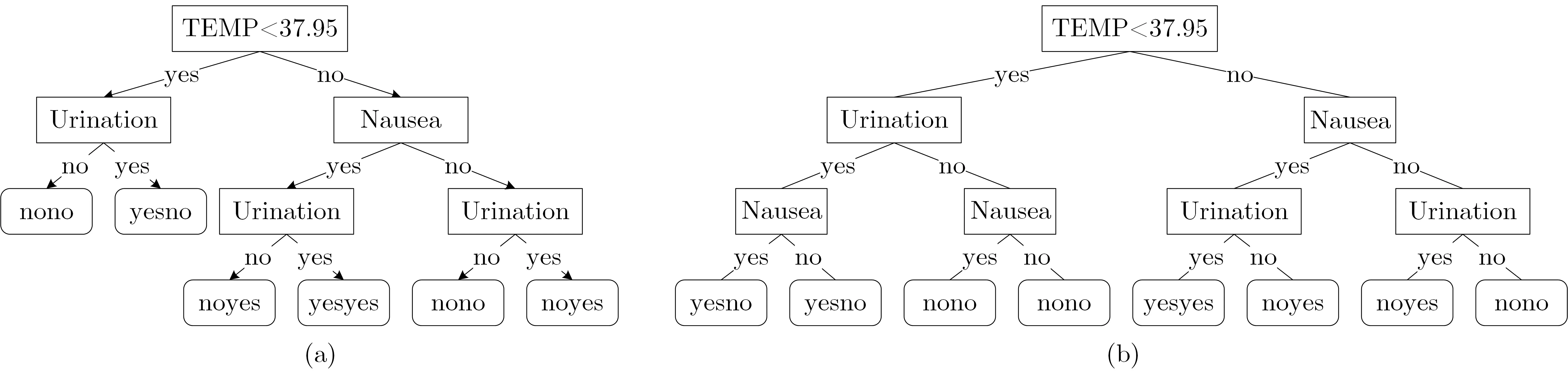
图4 决策树Figure 4 Decision trees

属性的排列与建立索引的方式均公开, 采用先序遍历的方法遍历决策树, 采用表4 的属性索引表, 建立索引之后服务器存储的数据如表5 所示.

假设客户端拥有的症状信息为{TEMP=37, Urination =‘no’, Nausea =‘yes’}, 则IC 的计算如下:

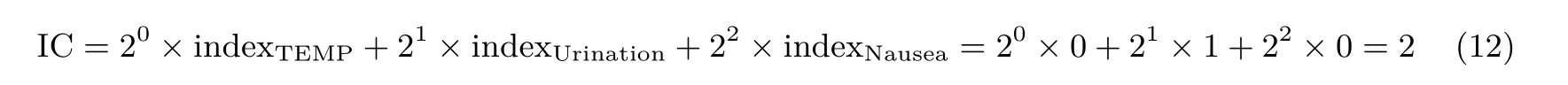
客户端使用索引IC = 2 (表示索引的值为2) 经过计算得到AIC= H1(IC)gaIC, 并将AIC发送给服务器(即查询时服务器只需要知道客户端的AIC). 因为服务器只知道客户端的AIC, 不可能根据AIC计算出客户端的IC. 因此, 此过程保护了客户端的IC(即保护了客户端的查询隐私).

服务器拥有决策树的每个等价类的症状索引以及对应的疾病类型. 服务器需要计算y = gx, DIC=(AIC)x=(H1(IC)gaIC)x, 并通过ci=mIndexi⊕H2(wxi) (其中mIndexi表示第i 个索引对应的疾病类型)计算决策树每个等价类对应的c1,c2,··· ,c8(中8 表示图4(b) 决策树中等价类的个数), 然后服务器将y、DIC与c1,c2,··· ,c8发送给客户端. 在此过程中, 客户端知道y 及c1,c2,··· ,c8, 并且只知道自身的DIC,因此, 客户端只能通过DIC得到IC = 2 对应的mIC, 而不会得到其它的任何信息. 即此过程保护了服务器的隐私, 使得客户端不知道除自身症状对应的疾病类型之外的其它任何信息.

表5 属性索引表Table 5 Index table of attributes

最后,客户端根据服务器传来的参数计算出KIC=DIC/yaIC,然后计算H2(KIC),再在c1,c2,··· ,c8中查找与H2(KIC) 值相等的H2(wxi) 对应的i = 3, 从而得出IC = 2 对应的c 的值为c3, 进一步得到索引IC 对应的疾病类型mIC= ‘nono’ (表示客户端输入症状对应的疾病类型为既没有患膀胱炎, 也没有患肾炎). 因为此过程由客户端计算, 因此服务器不知道客户端得到的是什么信息, 从而保护了客户端的隐私.

综上所述, 在整个查询过程中, 我们设计的基于OT 的双向隐私保护协议既保护了客户端的索引IC(即查询隐私), 也保护了服务器的隐私, 因为客户端在查询过程中只得到了与其查询症状相关的疾病信息, 而不能获得其它任何额外的信息.

5 安全性分析与性能评估

5.1 安全性分析

本文提出的医疗辅助诊断系统中新型的双向隐私保护主要提供三方面的隐私保护:

(1) 数据提供者的数据库隐私保护: 通过利用DT-Diff 算法对原始数据执行差分隐私保护后再构建决策树, 文献[1] 已经证明DT-Diff 算法可以实现ε-差分隐私保护.

(2) 客户端的查询隐私: 通过设计的基于OT 的隐私保护协议, 可以确保服务器只知道客户端的AIC,不能根据AIC计算出客户端的IC, 即不能知道客户端查询哪些症状属性, 从而保护客户端的查询隐私.

(3) 服务器的信息隐私: 通过设计的基于OT 的隐私保护协议, 客户端知道y 及c1,c2,··· ,cn, 并且只知道自身的DIC, 因此, 客户端只能通过DIC得到IC 对应的mIC, 而不会得到其它的任何信息. 即此过程保护了服务器的隐私, 使得客户端不知道除自身症状对应的疾病类型之外的其它任何信息.

5.2 性能评估

为了测试支持双向隐私保护的医疗辅助诊断系统的性能, 我们对该系统进行了实验. 实验的硬件平台为64 位Win 7 操作系统、CPU 频率2.60 GHz、RAM 为4 GB. 使用Python 开发语言, 数据库使用MySQL. 测试使用UCI 机器学习数据库中的Acute Inflammations 数据集, 实验分别从查询准确率、查询效率以及算法复杂度三个方面评估系统的性能.

Acute Inflammations 数据集包含8 个属性, 其中症状属性6 个, 类别属性2 个. 症状属性包含1个连续属性TEMP(表示患者的体温)、5 个文本属性分别为Nausea(表示是否恶心)、Lumbago(表示是否腰痛)、Urination(表示排尿是否持续)、U-pain(表示排尿是否疼痛) 与U-discomfort(表示尿道是否不适). 类别属性均为文本属性, 分别为Urocystitis (表示是否患膀胱炎) 与Nephritis (表示是否患肾源性肾炎). 数据集共有600 个元组(不含缺失值) 为训练数据, 其中100 个构成测试数据. 服务器构建的决策树如图5 所示. 从图5 中可以得出, 属性U-pain 与U-discomfort 的值不影响疾病诊断的结果.

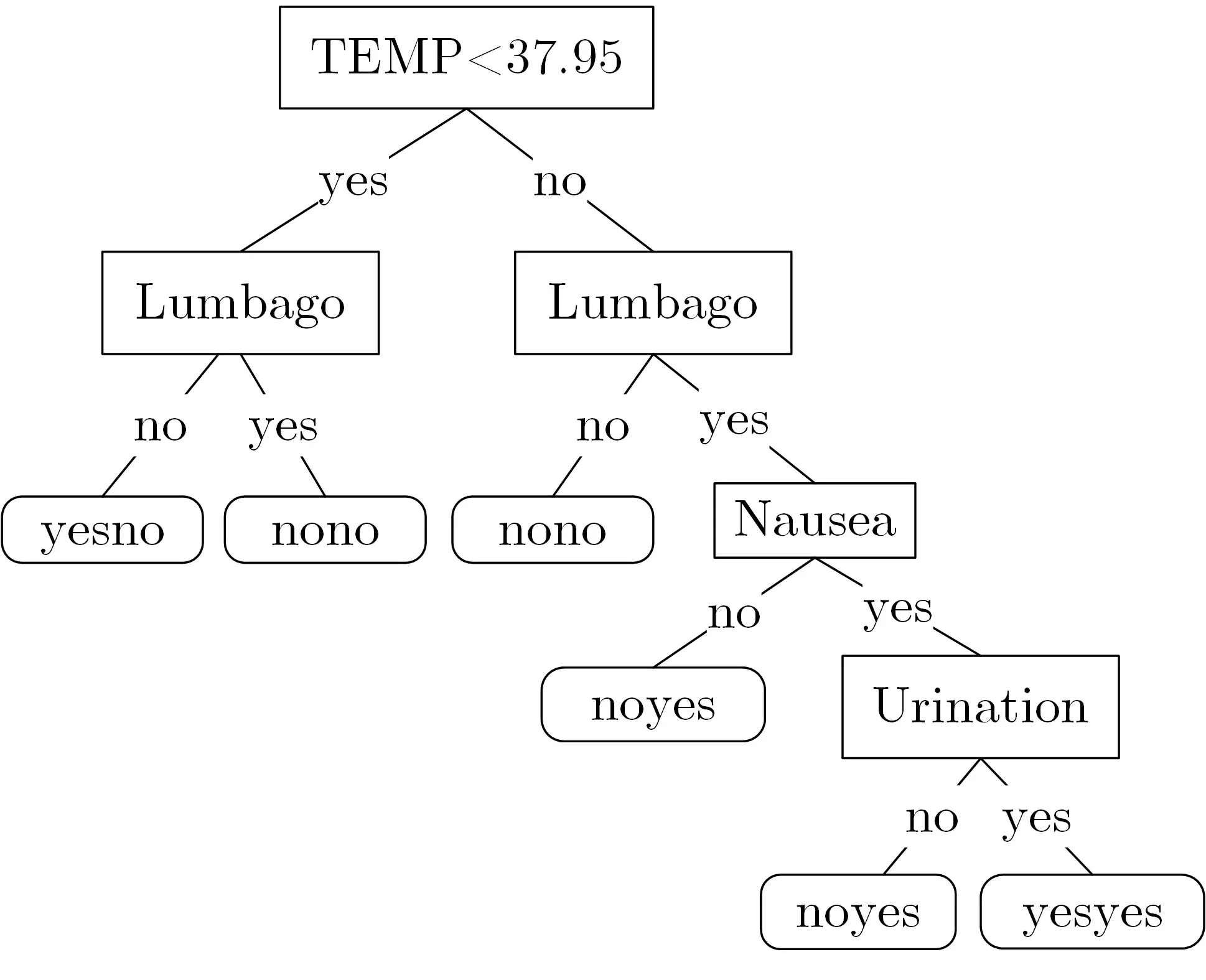
图5 服务器决策树Figure 5 Server decision trees

(1) 查询准确率

医疗辅助诊断系统的查询准确率取决于构建的决策树及其构建决策树时的隐私预算参数ε 和细分次数. 其中, 构建的决策树对查询的准确率影响较大, 而构建的决策树性能好坏取决于原始数据集. 在ε =0.02、0.05、0.1 与0.25, 细分次数分别为4、7、10、13 与16 时, 进行20 组实验. 当采用基于信息增益的可用性函数时, 其查询准确率与细分次数的关系如图6(a) 所示. 在ε = 0.02 时, 其查询准确率最低为75.6%, 最高为76.8%; 在ε=0.25 时, 其查询准确率最低为77.3%, 最高为79.5%.

图6 (a) 可用性函数为InfoGain(D,s) 时的查询准确率; (b) 可用性函数为MaxFS(D,s) 时的查询准确率Figure 6 (a) Query accuracy when the availability function is InfoGain(D,s); (b) Query accuracy when the availability function is MaxFS(D,s)

当采用基于最大频数和的可用性函数时, 其查询准确率与细分次数的关系如图6(b) 所示. 在ε=0.02时, 其查询准确率最低为78%, 最高为79.7%; 在ε=0.25 时, 其查询准确率最低为81%, 最高为83.7%.

差分隐私中隐私预算参数ε 越小, 其隐私保护强度越大, 即数据被扰动得越厉害, 则其查询准确率越低. 当隐私预算参数相同时, 细分次数越多, 查询准确率越高. 无论是采用哪种可用性函数, 其查询准确率都随着隐私预算参数的增大而提高, 而且两种可用性函数都是在细分次数为13 时, 其查询准确率最高. 随着细分次数的增加, 其查询准确率呈下降趋势. 原因在于当细分次数到达某个阈值时, 泛化结果中等价类的数量增加, 导致总体加入的噪声增加, 从而使得查询准确率下降. 实验结果表明, 采用基于最大频数和的可用性函数的查询准确率高于采用基于信息增益的可用性函数.

(2) 查询效率

在医疗辅助诊断系统中, 首先由服务器构建好决策树后, 客户端才能查询, 因此查询效率主要指执行双向隐私保护协议的查询效率, 并且与属性数量及连续属性的分类值有关. 因为离散属性的分类值是确定的, 因此查询效率与离散属性的分类值无关. 属性数量越多, 索引数据越多, 查询效率越低. 在属性个数相同时, 属性对应的分类越多, 索引数据越多, 查询效率越低.

图7(a)是提供双向隐私保护的系统的查询时间开销与查询次数的关系,其平均查询时间为0.0084 秒.与图7(b) 不提供双向隐私保护的系统的查询时间大约多了0.0074 秒. 因此我们提出的支持双向隐私保护的系统查询是高效的.

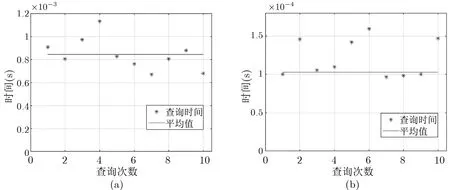
图7 (a) 支持双向隐私保护时的查询效率; (b) 不支持双向隐私保护时的查询效率Figure 7 (a) Query efficiency when two-way privacy protection is supported; (b) Query efficiency when two-way privacy protection is not supported

为了提高实验的准确率, 我们以10 次查询时间的平均值作为每组查询花费的时间. 图8(a) 显示属性个数与查询时间的关系, 实验结果显示, 在属性分类值个数相同的情况下, 属性个数越多, 查询时间越长,查询效率越低; 属性个数越少, 查询时间越少, 查询效率越高. 图8(b) 显示属性分类值个数与查询时间的关系, 在属性个数相同的情况下, 属性分类值个数越多, 查询时间越长, 查询效率越低; 属性分类值个数越少, 查询时间越少, 查询效率越高.

图8 (a) 属性个数与查询时间的关系; (b) 属性分类值个数与查询时间的关系Figure 8 (a) Number of attributes versus query time; (b) Number of attribute classification values versus query time

(3) 算法复杂度

假设数据集有k 个属性, 每个属性的分类个数为ai(1 ≤i ≤k), 那么在建立索引之后服务器拥有的数据集规模为a1×a2×···×ak.

本文使用的双向隐私保护协议是一个两轮协议, 客户端发送1 个消息, 通信复杂度为O(1). 服务器发送 a1×a2×···×ak+ 2 个消息, 通信复杂度为 O(a1×a2×···×ak), 因此总的通信复杂度为O(a1×a2×···×ak).

在进行数据查询时, 客户端执行2 次模幂运算, 服务器执行a1×a2×···×ak+2 次模幂运算, 因此总共执行a1×a2×···×ak+4 次模幂运算. 通常认为服务器提供强大的计算能力, 因此系统重点关注客户端的计算开销.

6 结论与下一步工作

本文最早提出结合决策树与OT 技术实现医疗辅助诊断系统中的双向隐私保护, 为了将OT 协议算法用于执行了隐私保护的决策树算法, 我们提出一种决策树索引协议, 可以高效地将决策树信息数字化,从而便于利用OT 协议保护客户端的隐私, 同时也可以保证客户端只能获得查询的相关信息, 而不能获得其它额外信息, 从而保护服务器的隐私. 实验结果表明提出的方法不仅具有较高的查询效率, 同时还具有较高的查询准确率. 下一步考虑如何在确保系统安全和效率的前提下降低系统的复杂性.