多输出弹性k-旋转对称布尔函数的存在性与构造*

田晔晨, 孙玉娟, 李路阳

1. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 西安710071

2. 密码科学技术国家重点实验室, 北京100878

3. 西安邮电大学 通信与信息工程学院, 西安710121

1 引言

由于k-旋转对称函数为旋转对称函数的扩展, 其数量多于旋转对称函数, 因此分析与研究k-旋转对称函数是一个具有重要理论意义的工作. 李泉等[18]在2012 年证明了k-旋转对称函数的Walsh 谱和自相关函数都满足k-旋转对称特性, 并且借助容斥原理给出了k-旋转对称函数轨道中的长圈与短圈的计数公式. 同年, 杜蛟和温巧燕等学者[19]通过矩阵分析的方法, 得到了2p 元2-旋转对称函数为弹性函数的一个充要条件, 完全确定了这类弹性函数的构造与计数方法, 其中p 为2 或奇素数. 2015 年, Liu 给出了一类仅由x1x2x3生成的三次2-旋转对称函数的汉明重量的递归式, 并证明了其非线性度等于其汉明重量[20].之后Reid 和Cusick[21]给出了由一个三次单项式生成的2-旋转对称函数的仿射等价类的划分. 2020 年Su[22]基于Rothaus’s bent 函数给出了构造n 维2-旋转对称bent 函数的两种方法, 其中n ⩾4.

由于多输出布尔函数在分组密码中的广泛应用, 具有特殊性质的多输出布尔函数在密码体制中逐步具有了重要的作用. 2009 年, 元彦斌和赵亚群[23]提出了多输出旋转对称函数的概念, 研究了多输出旋转对称函数的频谱及自相关函数的特征; 给出了多输出旋转对称函数满足平衡性, 相关免疫性等性质的充分必要条件; 并且通过研究奇数变元多输出旋转对称函数广义一阶Walsh 循环谱的性质, 得到了一种寻找奇数变元多输出Plateaued 旋转对称函数的方法. 之后Kavut 与高光普等学者将旋转对称函数与k-旋转对称函数用于构造S 盒, 分别利用穷搜索法[24]和最速下降法[25]得到了旋转对称S 盒或k-旋转对称S 盒的一些性质与结论, 并研究了置换或映射的结构. Mazumdar 等人[26,27]基于旋转对称函数构造出了具有高非线性度和高DPA 攻击抵抗力的旋转对称S 盒. 在平衡性与弹性方面, 杜蛟等[28]在2017 年给出了8元多输出旋转对称1 阶弹性函数的构造, 并给出了该类函数的计数方法. 基于此成果, 杜蛟等[29]随后通过求解方程组的方法, 给出了几类平衡与弹性多输出旋转对称布尔函数的存在性证明.

本文主要给出了几类平衡(0 阶弹性) 与1 阶弹性多输出k-旋转对称布尔函数的存在性与构造. 后文内容安排如下: 在第2 节中介绍了多输出旋转对称与多输出k-旋转对称布尔函数的相关基础知识, 在第3节中给出了多输出旋转对称与多输出k-旋转对称布尔函数轨道分布的计数公式. 第4 节主要提出了几种平衡多输出k-旋转对称布尔函数的存在性与构造. 1 阶弹性多输出k-旋转对称布尔函数的部分结论在第5 节给出. 第6 节对本文工作进行总结.

2 基础知识

其中1 ⩽i ⩽n.

其中k |n. 用d-轨道表示k-RSBF 中满足|Gn,k(x)|=d 的轨道Gn,k(x).

引理1[17]令gn与gn,k分别代表n 维RSBF 与k-RSBF 不同轨道的个数. 则有

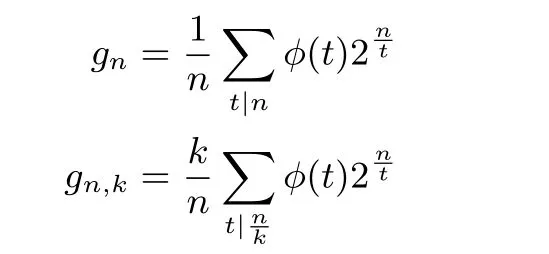
其中ϕ(t) 是欧拉函数.

由上述定义知,如果F(x)是一个(n,m)-RSBF,则对于任意的1 ⩽s ⩽m,均有fs(x)是一个RSBF.同样地, 若F(x) 是一个(n,m) k-RSBF, 则对于任意的1 ⩽s ⩽m, 均有fs(x) 是一个k-RSBF.

定义3[29]Gn(x) 与Gn,k(x) 中的所有向量按照如下方式分别排列成两个矩阵:

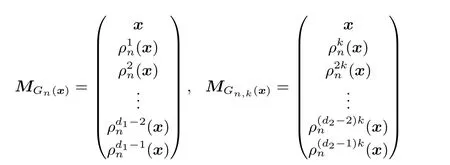
其中d1和d2分别代表Gn(x) 和Gn,k(x) 中向量的个数. 换言之, | Gn(x) |= d1, | Gn,k(x) |= d2.MGn(x)与MGn,k(x)分别称为Gn(x) 与Gn,k(x) 对应的轨道矩阵.

3 多输出旋转对称与多输出k-旋转对称布尔函数的轨道分布

本节研究了(多输出) 旋转对称函数和(多输出)k-旋转对称函数的轨道分布情况, 并给出了计算这两类函数中长度相同轨道个数的方法.

在文献[4] 中, Stănică 和Maitra 给出了RSBF 中部分大小的轨道的计数. 令hd表示n 维RSBF中大小为d 的轨道的个数, 其中d | n. 我们通过使用莫比乌斯变换, 给出RSBF 不同大小的轨道的计数公式, 扩展了文献[4] 的结论.

引理3

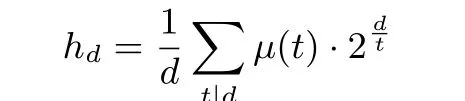
其中d|n, µ(·) 是莫比乌斯函数.

由等式(1)可计算出任意d 与k 所对应的hd,k. 我们列出一些n 维k-RSBF 的轨道分布, 如附录中表1 所示.

4 平衡多输出k-旋转对称布尔函数的存在性与构造

本节给出一些平衡(0 阶弹性) 多输出k-旋转对称布尔函数的存在性证明. 主要包含两部分: 一是2 ⩽m ⩽p 时(pr,m) p-RSBF 的存在性; 二是k 取pr和2pr−1时平衡(2pr,m) k-RSBF 的存在性. 此外还将给出一些其他关于平衡性的结论.

在引理4[29]中, 杜蛟等人给出如下结论: 若平衡(n,m)-RSBF 存在, 则平衡(n,m −1)-RSBF 存在.相反地, 如果不存在平衡(n,m −1)-RSBF, 则平衡(n,m)-RSBF 也不存在. 类似地, 这一结论也适用于(n,m) k-RSBF.

引理4 若平衡(n,m) k-RSBF 存在, 则平衡(n,m −1) k-RSBF 存在. 相反地, 如果不存在平衡(n,m −1) k-RSBF, 则平衡(n,m) k-RSBF 也不存在, 其中k 为常数.

证明: 证明方法与引理4[29]的证明方法相同. 出于篇幅的考虑, 此处不再详细证明.

定理2 当n=2pr, m ⩾2, r ⩾1, p 为奇素数时, 不存在平衡(n,m)-RSBF.

证明: 证明方法与定理2[29]的证明方法相同. 出于篇幅的考虑, 此处不再详细证明.

已知平衡(pr,m)-RSBF 不存在, 其中p 是奇素数[29]. 在(pr,m) k-RSBF 这类函数中, 令k =p, 则可得到如下结论.

定理3 令n=pr, 2 ⩽m ⩽p, k =p, 其中p 是奇素数, r ⩾2. 则平衡(n,m) k-RSBF 存在.

证明: 由引理4 知, 只需要证明平衡(pr,p) p-RSBF 的存在性(构造出平衡(pr,p) p-RSBF). 由等式(1)计算出(pr,p) p-RSBF 的轨道分布如下:

至此, 得到平衡(pr,p) p-RSBF. 进而由引理4 知, 当2 ⩽m ⩽p 时, 平衡(pr,m) p-RSBF 存在.

当2 ⩽m ⩽p −1 时, 平衡(pr,m) p-RSBF 可由以下方法得到: 任意一个平衡(pr,p) p-RSBF 有2p个原像集合. 将每2p−m个原像集合进行合并, 得到2m个大小相同的集合. 一个集合作为一个输出的原像, 即可得到平衡(pr,m) p-RSBF, 其中2 ⩽m ⩽p −1.

由定理2 知, 当m ⩾2 时, 不存在平衡(2pr,m)-RSBF. 然而, 如果选择恰当的k 与m, 则能够构造出平衡(2pr,m) k-RSBF.

定理4 设n=2pr,其中p 是奇素数,r ⩾1. (1)令k =pr,2 ⩽m ⩽n−1,则平衡(2pr,m)k-RSBF存在; (2) 令k =2pr−1, 2 ⩽m ⩽k, 则平衡(2pr,m) k-RSBF 存在.

证明: (1) 由等式(1)计算出(2pr,m) pr-RSBF 的轨道分布如下:

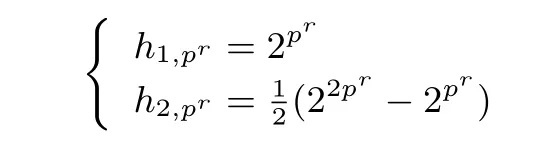
将每两个1-轨道合并为一个集合, 每1 个2-轨道单独作为一个集合, 则可得到

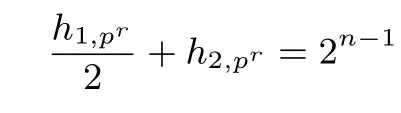
个集合,每一个集合包含2 个向量. 令一个集合作为一个输出的原像,即可得到平衡(2pr,n−1)pr-RSBF.因此, 平衡(2pr,n −1) pr-RSBF 存在. 进而由引理4 知, 当2 ⩽m ⩽n −1, r ⩾1 时, 平衡(2pr,m)pr-RSBF 存在.

当2 ⩽m ⩽n −2 时, 平衡(2pr,m) pr-RSBF 可由以下方法得到: 任意一个平衡(2pr,n −1) pr-RSBF 有2n−1个原像集合. 将每2n−m−1个原像集合进行合并, 得到2m个大小相同的集合. 一个集合作为一个输出的原像, 即可得到平衡(2pr,m) pr-RSBF, 其中2 ⩽m ⩽n −2, r ⩾1.

(2) 由等式(1)计算出(2pr,m) 2pr−1-RSBF 的轨道分布如下:

当2 ⩽m ⩽2pr−1−1 时,平衡(2pr,m)2pr−1-RSBF 可由以下方法得到: 任意一个平衡(2pr,2pr−1)2pr−1-RSBF 有22pr−1个原像集合. 将每22pr−1−m个原像集合进行合并, 得到2m个大小相同的集合.一个集合作为一个输出的原像, 即可得到平衡(2pr,m) 2pr−1-RSBF, 其中2 ⩽m ⩽2pr−1−1, r ⩾1.

由文献[28,29] 知, 当且仅当2 ⩽m ⩽2r−r 时, 平衡(2r,m)-RSBF 存在. 事实上当k = 2 时,(2r,m) k-RSBF 也存在, 且m 的取值范围为2 ⩽m ⩽2r−r+1.

定理5 当n=2r, 2 ⩽m ⩽2r−r+1, k =2, r ⩾2 时, 存在平衡(n,m) 2-RSBF.

证明: 我们利用数学归纳法进行证明.

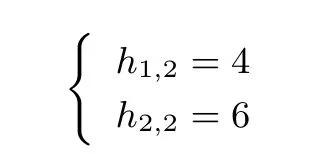
(1) 当r =2 时, (4,3) 2-RSBF 的轨道分布如下:构造平衡(4,3) 2-RSBF 等价于将全部轨道合并为8 个集合, 且每个集合有2 个向量. 将每两个1-轨道合并为一个集合, 一个2-轨道作为一个集合, 则可得到8 个集合, 且每个集合包含2 个向量. 将一个集合作为一个输出的原像, 即可构造出平衡(4,3) 2-RSBF.

(2) 假设可构造出平衡(2r−1,2r−1−r+2) 2-RSBF, 则可通过平衡(2r−1,2r−1−r+2) 2-RSBF 构造出平衡(2r,2r−r+1) 2-RSBF. 构造方法如下所示.

由等式(1)计算出(2r−1,2r−1−r+2) 2-RSBF 的轨道分布如下:

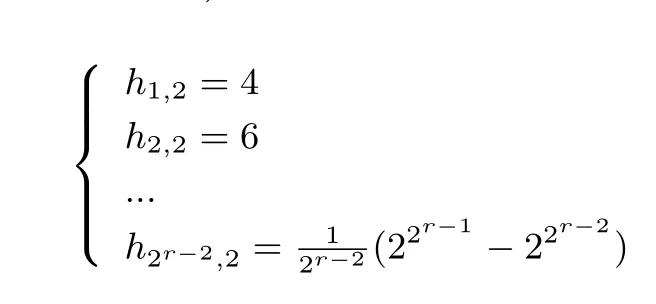
平衡(2r−1,2r−1−r+2) 2-RSBF 有22r−1−r+2个输出, 每一个输出对应的原像包含2r−2个向量. 换言之, 全部轨道被合并为22r−1−r+2个集合, 每个集合含有2r−2个向量.

当n=2r时, 由等式(1)计算出(2r,2r−r+1) 2-RSBF 的轨道分布如下:

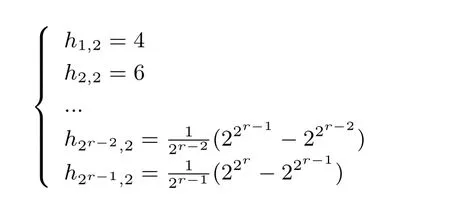
首先使用与(2r−1,2r−1−r+2) 2-RSBF 相同的轨道合并方法将(2r,2r−r+1) 2-RSBF 中全部的1-轨道, 2-轨道, 4-轨道, ···, 2r−2-轨道合并. 则可得到22r−1−r+2个集合, 每个集合包含2r−2个向量. 将上述集合两两合并, 则可得到22r−1−r+1个大小为2r−1的集合. 其次将每一个大小为2r−1的轨道单独作为一个集合. 至此, (2r,2r−r+1) 2-RSBF 的所有轨道被合并为22r−r+1个大小相同的集合. 每个集合作为一个输出的原像, 即可得到平衡(2r,2r−r+1) 2-RSBF. 进而可知, 平衡(2r,m) 2-RSBF 存在, 其中2 ⩽m ⩽2r−r+1, r ⩾2.

当2 ⩽m ⩽2r−r 时, 平衡(2r,m) 2-RSBF 可由以下方法得到: 任意一个平衡(2r,2r−r +1)2-RSBF 有22r−r+1个原像集合. 将每22r−r+1−m个原像集合进行合并, 得到2m个大小相同的集合. 一个集合作为一个输出的原像, 即可得到平衡(2r,m) 2-RSBF, 其中2 ⩽m ⩽2r−r, r ⩾2.

5 1 阶弹性多输出k-旋转对称布尔函数的存在性与构造

本节主要给出了1 阶弹性2r维及pr维多输出k-旋转对称布尔函数的存在性及构造方法. 并给出两个具体的例子进行验证. 为了便于描述, 引出如下符号定义. 设n 维k-RSBF 中由x = (x1,x2,··· ,xn)生成的轨道为

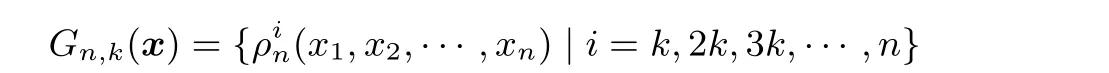
其中k |n. 则将n 维k-RSBF 中由x+1=(x1+1,x2+1,··· ,xn+1) 生成的轨道

证明: 证明方法与定理3[34]的证明方法相同. 并且由证明过程可知, d 为偶数.

在定理4[29]的证明中,杜蛟等人提出: 若1 阶弹性(n,m)-RSBF 存在,则1 阶弹性(n,m−1)-RSBF存在. 显然, 这一结论可扩展至多输出k-旋转对称布尔函数上: 若1 阶弹性(n,m) k-RSBF 存在, 则1 阶弹性(n,m −1) k-RSBF 存在, 其中k 为常数.

定理6 令n=2r, 2 ⩽m ⩽2r−r, k =2, 其中r ⩾3. 则1 阶弹性(n,m) k-RSBF 存在.

证明: 只需证明1 阶弹性(2r,2r−r) 2-RSBF 存在(构造出1 阶弹性(2r,2r−r) 2-RSBF).

1) 当r =3 时, n=8, 2 ⩽m ⩽5. 由等式1计算出(8,5) 2-RSBF 的轨道分布如下:

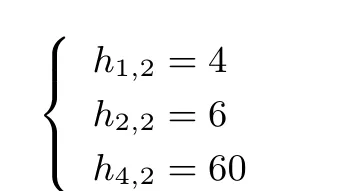
在60 个大小为4 的轨道里, 利用等式2计算可知仅有4 个特殊的轨道满足自互反特性, 其余的轨道均按照互反规则成对出现. 4 个特殊轨道对应的轨道矩阵如下所示. 将56 个成对的轨道按照互反规则两两合并, 得到28 个集合, 即得到28 个OA(8,8,2,1). 再将四个特殊的轨道任意两两合并可得2 个集合, 即得到2 个OA(8,8,2,1). 至此, (8,5) 2-RSBF 的全部轨道被合并为32 个大小相同的集合, 每个集合对应的矩阵均为一个OA(8,8,2,1). 一个集合作为一个输出的原像, 即可构造出1 阶弹性(8,5) 2-RSBF.

2) 设n=2r时, 1 阶弹性(2r,2r−r) 2-RSBF 存在. 则可证明n=2r+1时, 1 阶弹性(2r+1,2r+1−r −1) 2-RSBF 存在. 现给出由1 阶弹性(2r,2r−r) 2-RSBF 构造1 阶弹性(2r+1,2r+1−r −1) 2-RSBF的方法.

设1 阶弹性(2r,2r−r) 2-RSBF 的输出的原像对应的正交表为

定理7 设n = pr, 2 ⩽m ⩽p −1, k = p, 其中p 为奇素数, r ⩾2. 则1 阶弹性(n,m) k-RSBF 存在.

证明: 只需证明1 阶弹性(pr,p −1) p-RSBF 存在(构造出1 阶弹性(pr,p −1) p-RSBF).由等式(1)计算出(pr,p −1) p-RSBF 的轨道分布如下:

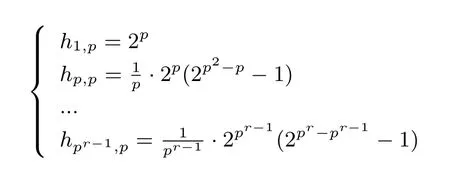
例2 设n = 32= 9, k = 3. 按照定理7 证明中的方法, 构造出一个一阶弹性(9,2) 3-RSBF:G = (g1,g2). g1与g2的真值表分别如下所示(十六进制). 由弹性的定义知, 函数F2也是平衡的, 符合定理3 的结论.

6 总结

本文研究了几类平衡与1 阶弹性多输出k-旋转对称布尔函数的存在性, 并在证明中描述了构造的方法. 多输出k-旋转对称布尔函数作为多输出旋转对称布尔函数的扩展, 除了囊括多输出旋转对称布尔函数的性质之外, 还存在部分多输出旋转对称布尔函数不具有的性质. 例如n=pr时, 选择合适的k 与m, 即可构造出平衡与1 阶弹性多输出k-旋转对称布尔函数. 在弹性性质方面, 目前只研究了1 阶弹性性质. 是否存在满足多阶或高阶弹性性质的多输出k-旋转对称布尔函数仍旧是一个有待研究的问题.