基于完美彩虹表的检查点算法改进研究*

于红波, 何 乐, 程子杰,2

1. 清华大学 计算机科学与技术系, 北京100084

2. 宾夕法尼亚州立大学 计算机科学系, 大学城, PA 16802

1 引言

哈希函数是一种可以将任意长度的私有数据映射为固定长度的哈希值的函数. 哈希函数在密码学领域中被广泛应用, 其中最为重要的应用场景之一就是口令认证. 为保障安全性, 哈希函数在设计上应具有单向性的特点: 即得到输入的哈希值十分容易, 而通过哈希值恢复对应的输入十分困难. 后者就是所谓的原像攻击, 在信息安全领域一直是一个热门的问题.

对于原像攻击, 最直接的解法就是穷举搜索. 假设目标哈希值的长度为n, 那么在期望上, 每2n次随机检索中就会出现一个对应的原像. 然而, 这种解法需要相当庞大的攻击时间以及计算能力. 为解决这一问题, Hellman[1]于1980 年提出了时间存储折中攻击方法, 该方法将预计算与穷举搜索相结合, 可以用额外的空间开销来换取攻击时间. 算法分为两个阶段: 预计算阶段和线上检索阶段. 在预计算阶段中, 攻击者进行大量的迭代计算以得到一系列的哈希链, 对每一条链仅仅保留链头和链尾两点, 舍弃所有中间节点(为节省空间). 当预计算工作结束后, 所得到结果即一张链表, 可以在多次检索中被重复利用. 对于一次线上检索(目标为分组密码的密钥或者哈希函数的原像), 攻击者只要完成相同的迭代操作, 直至目标与某一个链尾节点相匹配为止. 当二者匹配时, 攻击者就能利用已存储的对应链头节点恢复整条哈希链, 并期望没有经过迭代的原始目标恰好被该链所覆盖, 从而找到特定目标. 更多细节将在第2 节中进一步讨论.

然而, 由于链与链之间存在碰撞, 线上检索阶段可能出现问题. 可能的情况是, 原始目标并不在当前尾节点所匹配的哈希链中, 而是存在于另一条若干轮迭代后才会匹配的哈希链, 甚至是存在于一条根本未被预计算所生成的哈希链中, 这个现象被称为“误报”(false alarm). Hellman[1]曾指出, 由于碰撞这一固有缺陷, 误报所造成的时间损失能达到整个检索时间的50%. 2010 年, Hong[2]的论文表明, 在经典的Hellman 表中, 排除误报的时间代价占了整个检索时间的14.3%.

自Hellman 提出时间存储折中攻击方法后, 密码学家针对原方法做出了大量的改进和优化. Rivest[3]曾提出一种基于“特异点”(distinguished point) 的方法, 在该方法的规则下, 在预计算阶段生成哈希链时, 迭代操作直到某个符合特殊条件的特异点方会终止(例如首几个比特全部为0). 基于特异点模型,Kusuda 和Matsumoto[4]进一步分析了能将时间与存储协调的优化参数, 并将该方法应用于对DES 的攻击. Standaert 等人[5]同样对特异点模型进行了分析, 并完成了攻击40-bit DES 的FPGA 实现.

2003 年, Oechslin[6]从另一个角度进行改进, 提出了彩虹表算法. 相较于原始的时间存储折中攻击方法, 彩虹表主要解决了不同哈希链之间存在碰撞这一问题. 后者在每一列使用了不同的约减函数, 保证碰撞不会发生在彩虹表的不同列, 从而大幅减少碰撞的数量. 这一改进确实能大幅提升表在整个空间中的覆盖率, 同时也能降低发生误报的风险. 2005 年, Avoine 等人[7]提出了检查点算法(checkpoints method),算法在哈希链中段设置了一系列的检查点, 作为额外存储与链头和链尾一并保存. 在线上检索阶段, 目标除了要与链尾节点匹配之外, 所经过的检查点也必须一一匹配. 这样算法只需要分钟级别的额外开销, 就可以大幅降低发生误报所造成的损失, 从而提升算法效率.

在本文中, 我们借鉴了检查点算法的思想, 以完美彩虹表为基础, 研究并改进了对检查点效率的分析模型, 进而得到了复数检查点在完美彩虹表下的最佳理论位置. 尽管在一般的彩虹表应用, 如位数较多的用户口令破解中, 生成完美彩虹表需要不切实际的时间与空间开销, 但由于检查点算法本身对降低误报损失有着显著作用, 我们的结果对于一般的彩虹表仍具有一定启示性意义.

我们的工作总结如下:

• 我们研究并计算了彩虹表在整个空间中的覆盖率(即线上检索的成功率). 如果彩虹表表含有足够多的元素, 近似于完美表, 那么覆盖率只取决于表的数量. 我们发现当表的数量l ≥5 时, 覆盖率就能达到99.99%.

• 我们对检查点算法进行了理论分析, 推导出检查点最佳位置的计算式, 该计算式可以推广到任意数量的检查点. 进一步地我们计算了最佳位置下的理论收益, 并设置了实验进行验证, 同时选取了另外两个检查点集(均匀选取和Avoine 等人[7]的选取) 作为对照.

• 我们构造了实验来检验一些其它结论. 结果表明, 在l = 5 的条件下, 5 个检查点的时间收益可以达到30%. 此外, 在空间开销相当的条件下, 设置一个检查点的收益是额外生成新链的7 倍.

2 相关工作

这一节将简要介绍关于时间存储折中攻击的算法或概念. 下面的四个小节中, 讨论背景均假定为对于一个分组密码在选择明文攻击下的密钥恢复. 对于哈希函数的原像攻击, 算法的应用在本质上都是相同的.

2.1 原始的TMTO 方法

这一方法由Hellman[1]于1980 年提出. 算法分为两个阶段, 攻击者在预计算阶段构建一张链表, 然后在线上检索阶段利用它恢复密钥.

在预计算阶段, 攻击者交替地调用分组密码S 和一个约减函数R 来构造哈希链, 这等价于迭代调用f(K)=R(S(K,P0)), 其中K 为一个n-bit 的密钥, P0为攻击者所选择的明文. 注意R 本身是一个输出长度固定为n-bit 的函数, 所以f(K) 即为将整个密钥空间映射到自身的哈希函数, 迭代所得即一条条密钥空间中的哈希链. 具体而言, 对于一条哈希链(用一个序号i 来加以区分), 攻击者首先随机选取链头节点SPi= Ki,1, 然后进行若干步迭代计算Ki,j+1= f(Ki,j), 最终达到链尾节点EPi= Ki,t. 在构建了一系列的哈希链后, 只有那些链头节点(SP1,SP2,··· ,SPm) 和链尾节点(EP1,EP2,··· ,EPm) 会被保留下来. 这些节点隐式地存储了一张所谓的Hellman 表, 其结构与图1 中所示的彩虹表的结构十分相似. 由于链与链之间存在大量碰撞, Hellman 表在整个空间中的覆盖率十分有限. 为了提升覆盖率, 攻击者需要设置多张链表, 对应于不同的约减函数.

图1 彩虹表的结构Figure 1 Structure of rainbow table

在线上检索阶段, 为恢复目标密钥K0, 攻击者首先选择明文P0(与预计算阶段选择的明文相同), 并询问对应的密文C0=S(K0,P0), 然后计算

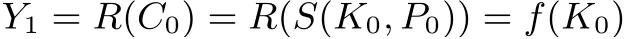
之后攻击者便检查是否存在某个链尾节点EPi与Y1相匹配, 如果不存在, 就不断地迭代计算Yj+1=f(Yj), 直至匹配某个链尾节点为止. 假设若干步之后, Ys= EPi成立, 这意味着f(s)(K0) = f(t−1)(SPi)成立. 由此, 攻击者期望K0= f(t−1−s)(SPi) = Ki,t−s同样成立, 这样就能从SPi中恢复出K0. 然而,由于f 并非是一一映射, 碰撞的存在可能使得两条不同的哈希链在Ki,t−s之后合并, 导致Ys虽与EPi匹配, 然而K0并不在对应的哈希链中. 这种现象就被称为“误报”. 具体而言, 哈希链中任何一个不同于K0的Ki,j, 只要满足f(c)(Ki,j)=f(c)(K0), 就会导致误报(其中c ≤t −j). 在实际情况中, 绝大部分的链尾节点匹配都是误报. 为了解决这一问题, 密码学家提出了许多改进.

2.2 彩虹表

彩虹表算法由Oechslin[6]于2003 年提出, 该方法可以大幅减少链与链之间的碰撞与合并. 在原始的TMTO 方法中, Hellman 在不同的表中使用不同的约减函数来提高覆盖率. 然而, 链与链之间的碰撞和合并依然大量存在. 例如Ki,p和Kj,q, 一旦二者相等, 由于同一张表中使用的约减函数相同, 链i 和链j 就会从碰撞处开始合并. 为了避免此类状况, 彩虹表在其结构上做了一个细微的变化: 设计不同的约减函数{R1,··· ,Rt−1}, 对每一列, 哈希链依次调用不同的Ri. 构造哈希链的迭代式变为:

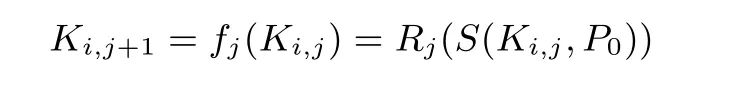
彩虹表的结构示意图见图1. 其中, t 是单条哈希链的长度, m 是单表中哈希链的数量. 在彩虹表中,上述所提到的碰撞和合并将大幅减少, 它们仅会出现在p = q 的情况. 也就是说, 碰撞与合并仅仅会发生在彩虹表的同列中, 这使得碰撞与合并的频率降低到原来的1/t.

2.3 完美表

由于Hellman 表中存在大量链与链之间的碰撞与合并, 存储整张链表所需的空间开销巨大, 而且有很大部分的重复和浪费. 为提升空间利用的效率, 攻击者可以额外计算足够数量的冗余链, 然后将发生碰撞和合并的链逐条删除, 余下两两没有碰撞的链. 这样攻击者就能在保证覆盖率的同时, 最大化地降低空间开销. 对于彩虹表, 消除合并的工作就变得更为简单. 攻击者只需要将所有EPi排序, 对EPi进行去重,尾节点相同的哈希链仅保留一条即可. 这个想法最早由Borst 等人[8]于1999 年提出, 消除合并后的链表就称为完美表. 在完成尾节点去重工作后, 攻击者所得到的完美彩虹表满足每一列中的所有元素互不相同. 当然, 在不同的列中依然会存在有相同的元素, 但由于不同列所使用的约减函数不同, 后续的合并将会被完全避免.

在2010 年, Hong[2]的论文指出, 完美彩虹表和非完美彩虹表中由误报所造成的时间损失分别占到检索时间的25.8% 和27.6%, 二者的差距并不大. 此外, 完美彩虹表具有良好的性质, 抹除了一些复杂的因素(如不同列之间的碰撞), 这使得理论分析更加简便和直观. 因此, 在本文接下来的部分, 我们关于检查点算法的分析和讨论均主要基于完美彩虹表.

2.4 检查点

2005 年, Avoine 等人[7]提出了检查点算法, 他们认为如果判断一次匹配是否为误报总是需要t −s的开销(即恢复哈希链到Ki,t−s的位置), 算法效率很难有显著的提升. 借助检查点, 攻击者就可以“提前”侦测到误报, 从而降低时间开销.

假定检查点的选取位置为α, 对应的值为Xj,α. 在预计算阶段, 对于每一条链, 除了头尾两个节点外,攻击者还将对每个检查点位置的哈希值计算对应的G 函数, 将G(Xj,α) 一并保存. 在线上检索阶段, 当某个Ys= EPj匹配时, 攻击者先检查每个经过的检查点是否满足G(Yα+s−t) = G(Xj,α)(经过的检查点即α > t −s 的点). 如果其中任何一个检查点没有满足该等式, 攻击者便可以认定其为一次误报. 这是因为G(Yα+s−t)= G(Xj,α) 意味着Yα+s−t= Xj,α, 又Yα+s−t= f(α+s−t)(K0) 且Xj,α= f(α+s−t)(Kj,t−s),故能得知K0=Kj,t−s(在彩虹表中, f(α)(K) 指ft−1(ft−2(···ft−α(K)))).

当然, 即便所有检查点都通过了检查, 攻击者也无法断定这次匹配不是误报, 因为碰撞可能恰恰发生在Kj,t−s和它右侧的检查点之间. 图2 和图3 显示了检查点和碰撞发生点处在不同位置时的效果. 如图2,碰撞发生在检查点之后, 那么检查点所存储的哈希值就与线上检索阶段所生成的哈希链对应元素不匹配,也就是G(Yα+s−t)̸=G(Xj,α), 误报被成功侦测. 若如图3, 碰撞发生在检查点之前, 导致Yα+s−t=Xj,α,自然G(Yα+s−t)=G(Xj,α), 误报侦测失败.

至于G 函数的选择问题, 为使算法在空间和时间上更加高效, G 函数应被设计为具有易于存储和计算的形式. 例如选择G(X) = X, 存储全部信息, 则空间代价将成倍地增长, 比较效率也很低. Avoine 等人[7]在论文中建议取G(X) 为X 的最低位比特, 当然这种方式会引入额外的侦测失败概率. 对于本不应通过检测的检查点, 在这种方式下能成功侦测到误报的概率为:)

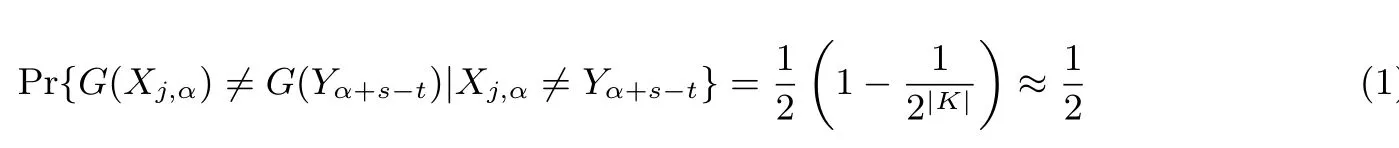
图2 误报侦测成功Figure 2 False alarm detection success

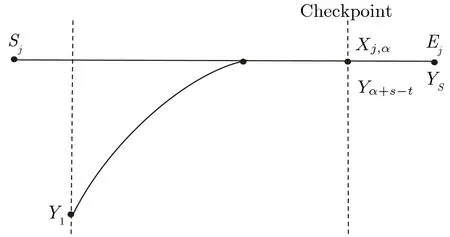
图3 误报侦测失败Figure 3 False alarm detection failure

3 检查点算法分析

这一节中, 我们将对检查点算法的效率进行全面分析, 包括单个或多个检查点所带来的时间增益, 以及检查点的最佳位置选取. 作为分析的基础, 我们也将讨论彩虹表的覆盖率以及误报所造成的时间损失.

3.1 列覆盖率

覆盖率是彩虹表算法成功概率的体现. 只有已经被彩虹表所覆盖, 即在预计算阶段所涉及到的元素(原像或密钥) 才能被彩虹表成功恢复, 反之, 只要是彩虹表中的元素, 经过有限次误报后总是能被正确匹配. 至于误报发生的次数, 造成的时间损失, 匹配的迭代轮数等, 都与该元素所在的深度, 即其所在的列有关(若元素在彩虹表中出现多次, 则为最靠近链尾的列). 一般而言, 元素越靠近链尾, 误报发生的次数越少, 单次误报损失越大, 所需的迭代轮数越少. 若要更深入地讨论这些问题, 首先要解决的是目标处在彩虹表中每一列的期望概率.

定义符号Rj为第j 列的列覆盖率, 它表示自该列起直至链尾, 彩虹表所有不同元素个数与整个空间元素个数的比值. 换言之, Rj就是彩虹表算法在不超过t −j +1 轮迭代下的成功率, 而目标恰处在第j列的概率就为Rj−Rj+1. 在此再确认一下相关符号和概念: m 为单表中哈希链的条数, t 为单条哈希链的元素个数, N 为整个空间的元素个数. 假定我们的链表是一张极大完美彩虹表. Oechslin[6]曾证明, 给定足够大的链长t, 彩虹表中不造成链合并的最大链数为mmax(t)=2N/(t+2). 因此, 我们有2N =mt.

记mi为彩虹表中第i 列不同元素的个数. 第i 列的元素为第i −1 列的元素向整个空间经f 映射而来, 这相当于一个有放回的抽取模型. 于是对于一个空间中的元素, 其出现在第i 列的概率就是:

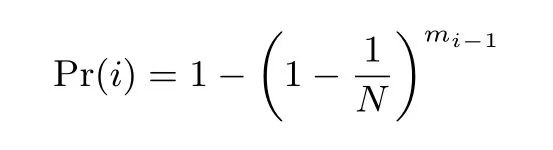
因此数列{mi} 就满足递推关系mi= N ∗Pr(i), 起始项m1= m(因为表头是攻击者可选的). 当然这个结果只是对于一般的彩虹表, 对于完美彩虹表, 同一列中没有碰撞, 总是有mi= m. 这个结果一方面表明在相同条件下, 完美彩虹表确实有更高的空间利用率, 另一方面也给完美彩虹表下的分析带来启发.

从中可以得出:

对于全表即j = 1, 当t 足够大的时候, R1可以化简为R1= 1 −e−2. 换言之, 对于一张极大完美彩虹表, 依然存在e−2的未覆盖空间. 对于使用了不同约减函数集的l 张完美彩虹表, 未覆盖空间为e−2l,对应覆盖率为1 −e−2l. 当l = 5 的时候, 覆盖率即可达到99.99%, 几乎可以近似认为覆盖了空间中的所有元素. 因此在本文所构造的实验环境中, 我们同样选择l =5.

3.2 误报损失

在上节, 我们已经分析了目标在第j 列匹配的概率, 为Rj−Rj+1(补充定义Rt+1= 0). 注意迭代与匹配是从链尾即第t 列开始的. 在这一节, 我们将进一步讨论误报所造成的时间损失.

在线上检索阶段, 一次链尾匹配意味着两种可能: 少数情况的正确匹配以及大多数情况的误报. 而误报是由线上检索时计算的迭代链与匹配链之间的碰撞所引发的. 根据完美彩虹表的性质, 我们可以计算两条链恰碰撞于第c 列的概率, 为:

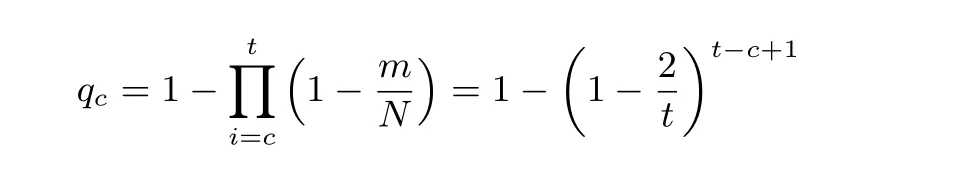
记Q(x) 为误报所造成的额外损失, 其中x 为目标所在的列号(对应于匹配的迭代轮数, 二者之和为t+1). 现目标经t+1 −x 轮迭代后与某个链尾节点匹配, 碰撞必然发生在第x 列到第t 列之间的某个位置, 而在无检查点的情况下, 检查第c 列的碰撞又需要c 的代价. 这也就意味着:

又由上节, 目标在第j 列匹配的概率为Rj−Rj+1. 故误报的期望损失为该概率乘以Q(j), 对j 遍历求和得到. 然而这种计算方式遗漏了一种情况, 即目标根本未被彩虹表所覆盖的情况, 在该情况下, 导致误报的碰撞可能发生在任何一列, 这与Q(1) 等价. 综上所述, 一次误报所造成的期望时间损失就为:

3.3 检查点收益

基于以上讨论, 这一节我们开始分析检查点算法所带来的时间增益, 包括单检查点的情况和多检查点的情况. 首先考虑单检查点的情况. 根据之前对检查点算法的描述, 只有线上检索生成的迭代链所经过的检查点才能生效, 过深(过于靠近表头) 的检查点没有判断的意义. 此外, 对于有效的检查点, 必须在G 函数结果不同时才算侦测成功, 如果采用式(1)的结果, 成功概率为1/2.

计gα(s) 为检查点在第α 列, 匹配在第s 列时的检查点生效概率. gα(s) 的计算见式(2).

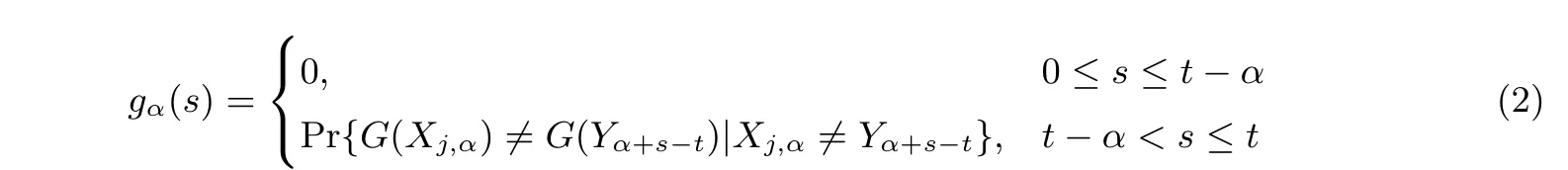
在有检查点情况下, 单次误报的时间损失就变为:

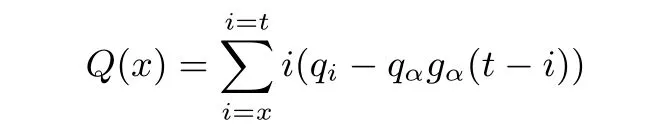
其中qαgα(t −i) 即为检查点算法生效, 免去花i 步验证碰撞所带来的收益部分.

再看多检查点的情况, 假定其位置从右到左依次为α1,…,αn. 多检查点的收益部分如式(3)所示.

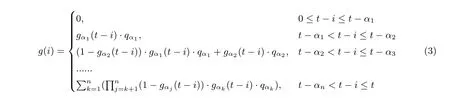
代入gα(c)≈1/2, 上式可简化为:

3.4 最佳位置

这一节我们进一步讨论最佳位置的计算. 首先还是看单检查点的情况. 将式(4)中的TG 按g(t −tx)的取值分段展开, 得到:

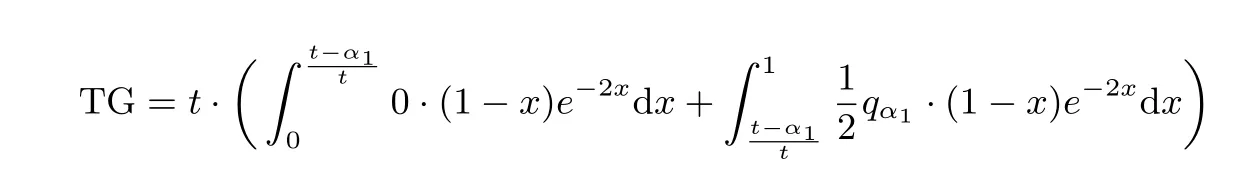
含有n 的情况难以得到简洁的形式, 只能代入特定的n 求出最优解析解. 分别取n = 2,3,4,5, 对应的TGn如下式所示.

最终, 所求得的最佳位置如表1 所示.

表1 检查点的最佳位置Table 1 Optimal positions of checkpoints

此外, 图4 显示了不同检查点数量下, 时间收益的变化趋势, 其横坐标为检查点数目, 纵坐标为提取出固定系数的标准化TG. 从图中可以看出, 时间收益随检查点数目的增长而增长, 但是每个单独检查点的收益是在逐步下降的.

4 实验设计与结果分析

在进行了大量的理论计算后, 我们同样设计了实验来验证我们的理论分析. 测试主要集中在两个方面,一是测试不同列下的覆盖率是否与我们的分析相符合, 二是测试不同检查点选取方案的效果并进行比较.

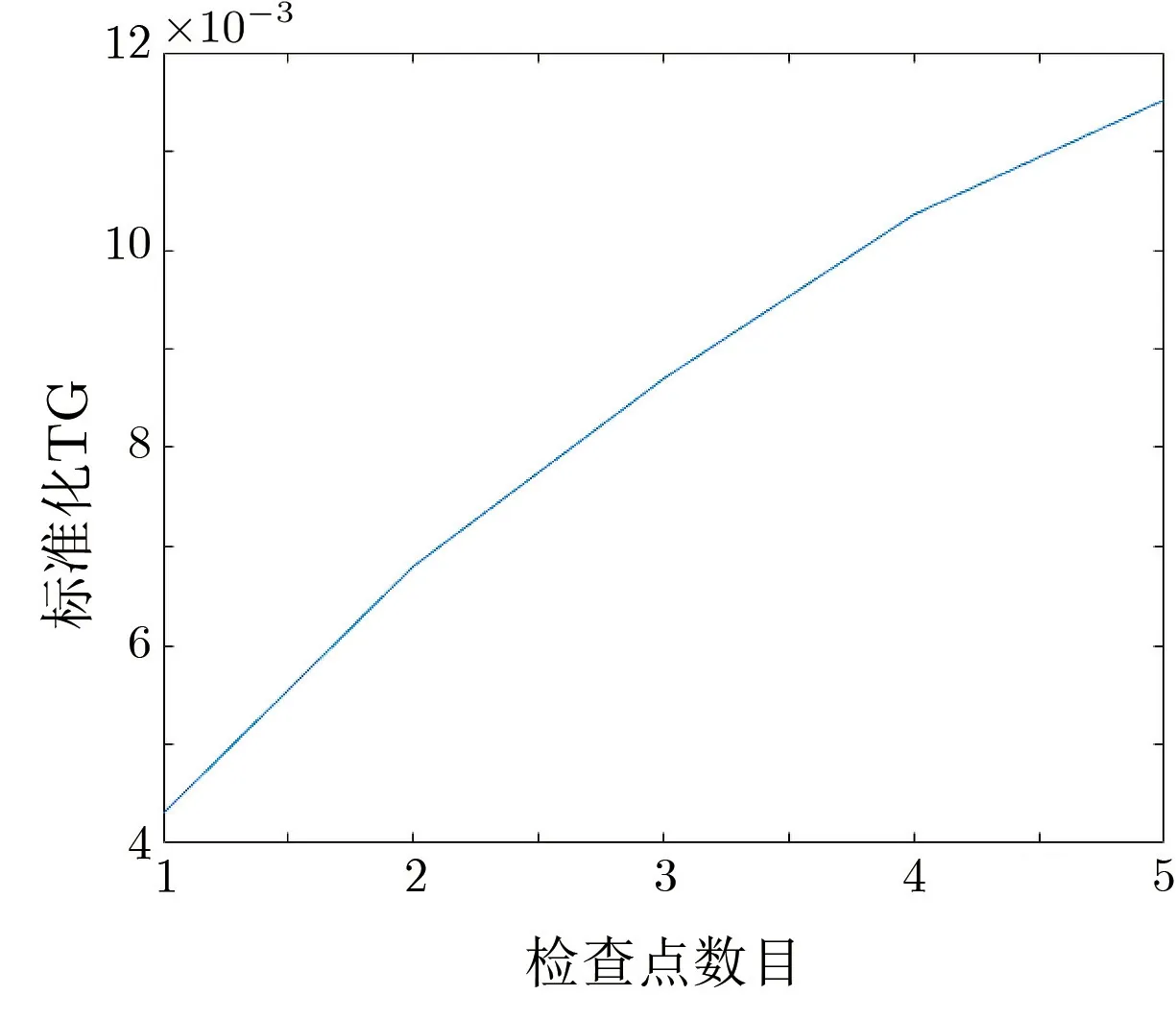
图4 不同数量检查点下的时间收益Figure 4 Total time gain under different checkpoints number

实验之前我们首先构造了数张完美彩虹表. 相较于分组密码, 哈希函数加密效率高又不需要私钥, 且本质上彩虹表算法在二者的应用上没有区别, 故我们选择使用哈希函数来代替分组密码进行测试. 以下为实验用完美彩虹表的相关规格说明: 所选哈希函数为标准SHA-1, 原像空间为7 位的ASCII-32-95, 彩虹表数量l =5, 每张表链数m=107 374, 链长t=10 000.

逐列计算每一列中新元素的个数, 并与不同深度下的理论覆盖率1 −e−2ld比较, 结果见表2.

表2 理论覆盖率与实际覆盖率比较Table 2 Comparison of theoretical coverage and actual coverage

验证检查点理论最佳位置的效果是实验的主要任务. 除了直接测试我们的最佳位置选取方案之外, 我们还设置了对照实验来比较不同选取方案的效果. 表3 给出了三种检查点的位置选取方式, 其中第三种为本文中的选取方式, 与表1 相同, 而Control 1 和Control 2 分别为均匀选取和来自Avoine 等人[7]论文中的选取方式.

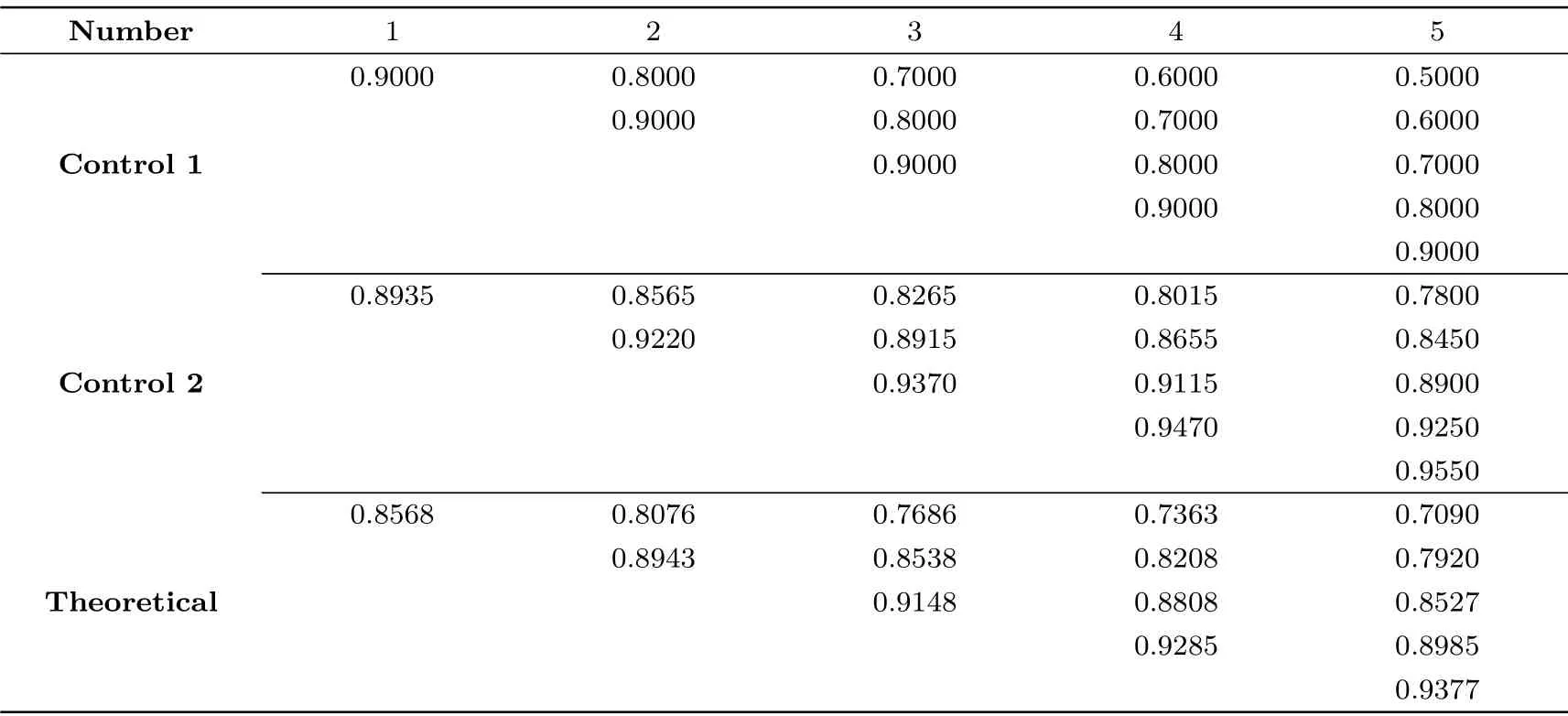
表3 三种检查点位置集合Table 3 Three sets of checkpoints position

表4 为关于本文所提出的最佳位置选取方案的相关测试结果, 包括检查点的额外空间开销, 空间开销转化为新链的收益, 最佳位置选取方案的理论收益与实际收益四项. 表5 为l =4 下, 对比三种选取方案的横向测试结果.

表4 l=5 的实验结果Table 4 Experiment results at l=5

表5 l=4 的对比结果Table 5 Comparison results at l=4

在此总结上述所有实验结果. 首先, 关于检查点算法本身的效率, 在相同的空间开销下, 使用检查点算法的收益要远远高于产生新链的收益. 其次, 当采用合适的选取策略时, 检查点的收益能在一定程度上得到提升. 虽然差距只有一点点, 我们所提出的策略看起来依然是最为高效的. 最后, 随着所处位置的深度提升, 不同检查点带来的收益会不断下降. 换言之, 随着检查点数目的增长, 最靠近表头的检查点的收益会越来越低.

5 总结

本文主要研究了完美彩虹表中的检查点算法, 对算法进行改进, 使之尽可能高效地降低误报所造成的时间损失. 在本文中, 我们的研究涉及以下几个方面. 我们首先分析了多张彩虹表中覆盖率与所处深度的关系, 从而得到元素于不同列中匹配的概率. 进一步地, 我们推导出单次匹配中由误报所造成的期望时间损失, 以及检查点所带来的期望时间收益的表达式. 基于该表达式, 我们进行近似分析和最优化求解, 提出了n = 1 到n = 5 的最佳位置选取策略. 最后, 我们设置了相关实验来验证理论分析的结果, 结果显示我们的策略要优于已有的结果, 最高能带来30% 的时间收益.