紧致安全的基于身份的签名方案*

刘翔宇, 刘胜利,3, 谷大武

1. 上海交通大学 计算机科学与工程系, 上海200240

2. 密码科学技术国家重点实验室, 北京100878

3. 成都卫士通信息产业股份有限公司摩石实验室, 北京100070

1 引言

在可证明安全中, 密码学方案总是基于某些困难问题, 且其安全性是通过安全归约证明来实现的. 安全归约的思路如下: 如果存在某个运行时间为t 的敌手A 能以优势ϵ 攻击某个密码方案S, 我们通过调用算法A 构造出另一个运行时间t′的算法B, 使得算法B 以ϵ′的优势解决某个困难问题P. 参数L := (t′ϵ)/(tϵ′) 定义为安全归约中的损失因子. 在安全归约中, 一般要求L 是一个关于安全参数λ 的多项式. 因为问题P 的困难性假设认为不存在算法可以在多项式时间内解决问题P, 所以密码方案S 不存在多项式时间的敌手A, 故而证明了S 的安全性. 当t′=Θ(t) 时, 归约损失因子可等价定义为L:=ϵ/ϵ′.如果L 是一个常数, 那么此安全归约是紧致的. 如果L=O(λ) (λ 为安全参数), 归约是几乎紧致的. 在很多签名方案(Signature, 简称SIG) 中, 松散安全归约的损失因子L 与敌手得到的签名数Q 及其涉及的用户数µ 紧密相关. 假设L ≈240, 这就造成了一个很大的安全损失. 为了弥补这个损失, 在密码方案的实施过程中, 我们需要选择更大的安全参数, 导致元素尺寸的增大和计算次数的增加, 从而降低算法的效率.因此, 近些年来的许多密码方案都在追求紧致安全性[1–9].

基于身份的签名(identity-based signature, IBS) 方案最早由Shamir[10]提出. IBS 的实施通常建立在一个群组中, 群组管理员产生主公钥mvk 和主私钥msk, 并借助msk 为每个用户产生一个与其身份id 关联的私钥skid. 用户可以用skid产生对消息m 的签名σ, 任何验证者可以结合主公钥mvk 和相应的id, 对(m,σ) 进行验证. 通常一个签名方案的基本安全要求是“选择消息攻击下的不可伪造性” (简称EUF-CMA 安全). 该安全性是指, 即使某一敌手得到了多个消息签名对, 他也很难伪造出一个新消息的合法签名. 在基于身份的签名方案中, 敌手还可能冒充某个身份, 从群组管理员中获得其身份私钥. 因此, IBS 安全性要求是: 对于用户id∗, 只要敌手不知道其私钥skid∗, 那么即使敌手得到多个由skid∗产生的消息签名对, 他也很难伪造一个针对id∗的新消息的签名, 这就是EUF-CMA&CIA 安全(正式定义见第2 节).

紧致安全的签名方案分为单用户和多用户场景(基于身份的签名方案默认为多用户场景). 单用户场景下的紧致安全要求其安全损失因子与敌手得到的签名数Q 无关(紧致EUF-CMA 安全); 多用户场景下的紧致安全不仅要求损失因子与Q 无关, 还要求与用户数无关(紧致MU-EUF-CMA 安全). 目前已有许多紧致安全的签名方案的研究. 在单用户场景的紧致安全方面, Cramer 和Damgård[1]基于RSA 假设给出了第一个紧致EUF-CMA 安全的签名方案. 随后出现了许多基于树结构的紧致安全的签名方案, 如文献[2–7], 另外, 紧致安全的签名方案可由紧致安全的基于身份的加密方案导出, 如文献[11,12]. 近年来,还出现了利用非交互零知识证明构造的紧致安全签名方案, 如文献[13,14]. 在多用户场景的紧致安全方面, Hofheinz 和Jager[4]基于DLIN 假设构造了第一个紧致MU-EUF-CMA 安全的签名方案. 随后, 张等[7]将其扩展为一个通用构造, 并在MDDH 假设和DCR 假设下给出了具体实例. 在基于身份的签名方面, 目前鲜有紧致安全的研究. Kiltz 和Neven 在文献[15] 中总结了IBS 的三种通用构造方法, 分别基于证书思想[16], 身份认证协议和分层的基于身份的加密方案, 但其构造都没有考虑紧致安全性. 已有的一些IBS 的具体构造如文献[17–19] 等, 其安全归约都是松散的. 张等在文献[7] 中给出了第一个紧致(弱)安全的IBS, 他们在IBS 的安全性定义中要求, 若敌手得到了某个id 下的消息签名对后, 不能再获取此id 对应的私钥skid, 因此方案实际上只达到了弱EUF-CMA&CIA 安全性. 目前, 还没有真正意义上紧致EUF-CMA&CIA 安全的基于身份的签名方案.

本文主要研究如何实现紧致安全的IBS. 我们进一步研究了文献[15] 的第一种通用构造方法, 即Bellare 等人[16]所提出的基于证书思想的通用转化方法, 结合一个紧致EUF-CMA 安全的签名方案S和一个安全性更高(紧致MU-EUF-CMAcorr安全, 见第2 节) 的签名方案˜S, 构造了第一个紧致EUFCMA&CIA 安全的基于身份的签名方案. 与文献[15,16] 的通用构造相比, 我们的目标是追求紧致安全特性, 因此对子组件的安全要求不同, 安全归约证明过程也有所差异. 我们分别在随机预言机模型(random oracle model) 和标准模型(standard model) 下给出相应的具体实例, 主要工作如图1 所示.

图1 构造与实例化Figure 1 Construction and instantiations

2 预备知识

本节给出(常规) 签名方案与基于身份的签名方案的定义及安全性要求. 首先对符号做说明如下. 用λ 表示安全参数; 对于自然数µ, 用[µ] 表示集合{1,2,··· ,µ}; 用x$←−X 表示从集合X 中均匀随机地选取x; 用y ←A(x) 表示输入x 运行算法A 并将结果赋值给y; 用∅表示空字符; 用|| 表示串联符号; PPT 是概率多项式时间的缩写; poly(·) 为多项式函数; 可忽略函数negl(·) 定义为当λ 足够大时, 都有negl(λ)<1/poly(λ).

2.1 签名方案及其安全性

定义1 (签名方案) 一个签名方案S=(Setup,KGen,Sign,Ver) 由如下四个算法组成:

• Setup(1λ): 预备算法输入安全参数1λ, 输出公开参数pp. 假定pp 为Sign 和Ver 的一个隐式输入.

• KGen(pp): 密钥生成算法输入pp, 输出一对验证公钥/签名私钥(vk,sk).

• Sign(sk,m): 签名算法输入私钥sk 和消息m, 输出一个签名σ.

• Ver(vk,m,σ): 验证算法输入公钥vk, 消息m 和签名σ, 输出一个比特, 1 代表σ 是消息m 的一个合法签名, 0 代表不合法.

正确性: 对任意pp ←Setup(1λ), (vk,sk)←KGen(pp), 任意消息m, 都有Ver(vk,m,Sign(sk,m))=1 成立.

针对一个签名方案, 敌手可能会自主选择一些消息, 并获得这些消息的相应签名. 不可伪造性要求即使敌手看到了这些消息签名对, 他也不能对一个新的消息伪造出合法签名. 安全定义具体如下.

定义2 (EUF-CMA 安全) 对签名方案S=(Setup,KGen,Sign,Ver), 定义敌手A 在选择消息攻击下的攻击优势

一般签名方案都部署于多用户场景. 即敌手会看到多对(用户) 公钥, 他可以选择某一用户进行攻击.在某些多用户应用场景如认证密钥交换中, 敌手还可以动态地窃取部分用户的私钥sk, 方案安全性在这时要求没有被窃取密钥的那些用户(以及对应公私钥) 下的签名的不可伪造性, 即MU-EUF-CMAcorr安全[8]. 安全定义具体如下.

定义3 (MU-EUF-CMAcorr安全) 对签名方案S = (Setup,KGen,Sign,Ver), 定义敌手A 在多用户场景中选择消息攻击& 动态密钥窃取攻击下的攻击优势

如果在定义3 中A 只有签名预言机OSign(·,·) 没有OCorr(·), 那么S 对应具有多用户场景中选择消息攻击下的不可伪造性, 即MU-EUF-CMA 安全. 通过混合论证我们得知, 签名方案的EUF-CMA 安全性隐含了MU-EUF-CMAcorr安全性, 不过其归约证明会有一个损失因子µ, 因此不具有紧致安全性.

2.2 基于身份的签名方案

定义4 (基于身份的签名方案) 一个基于身份的签名方案IBS = (Gen,Ext,Sign,Ver) 由如下四个算法组成:

• Gen(1λ): 主密钥生成算法输入安全参数1λ, 输出主公钥/主私钥(mvk,msk). 默认msk 中包含了mvk 的信息.

• Ext(msk,id): 密钥提取算法输入主私钥msk 和某一用户id, 输出此id 对应的身份私钥skid.

• Sign(skid,m): 签名算法输入某一身份私钥skid和消息m, 输出一个签名σ.

• Ver(mvk,id,m,σ): 验证算法输入主公钥mvk、用户id、消息m 和签名σ, 输出一个比特, 1 代表σ 是在此id 下对m 的一个合法签名, 0 代表不合法.

正确性: 对任意(mvk,msk) ← Gen(1λ), 任意id 和skid← Ext(msk,id), 任意消息m, 都有Ver(mvk,id,m,Sign(skid,m))=1 成立.

在基于身份的签名方案的应用中, 敌手除了可以动态获得某些指定消息的签名外, 还有可能获得某些用户的身份私钥, 在此时我们要求对于那些未泄露私钥的用户, 其签名是不可伪造的. 安全定义具体如下.

定义5 (EUF-CMA&CIA 安全) 对基于身份的签名方案IBS=(Gen,Ext,Sign,Ver), 定义敌手A 在选择消息攻击& 选择身份攻击下的攻击优势

目前已有的一些基于身份的签名方案, 如文献[16,17] 等, 都不具有紧致安全性. 第一个紧致安全方案的尝试为文献[7], 但他们仅仅达到了一个弱EUF-CMA&CIA 安全, 即安全性定义要求敌手在问询了id 相关的签名预言机之后, 不能问其对应的密钥提取预言机. 上述弱安全性可通过混合论证推导出(常规)EUF-CMA&CIA 安全性, 但会有一个损失因子µ (敌手在签名和密钥提取问询时所涉及的最大用户数).因此, 目前实际上没有真正紧致安全的基于身份的签名方案的构造.

3 紧致EUF-CMA&CIA 安全的IBS 的通用构造与安全证明

Bellare 等人在文献[16] 中提出了由(常规) 签名方案到基于身份的签名方案的通用转化方法, 他们使用的组件为EUF-CMA 安全的签名方案. 本节, 我们借助文献[16] 中的基于证书思想的通用转化方法, 提出了一个基于身份的签名方案的通用构造. 我们所使用的模块为EUF-CMA 安全的签名方案S 和MU-EUF-CMAcorr安全的签名方案˜S, 且构造出的IBS 的安全性可以紧致归约到S 和˜S 的安全性.

3.1 构造方案

设S = (S.Setup,S.KGen,S.Sign,S.Ver), ˜S = (˜S.Setup,˜S.KGen,˜S.Sign,˜S.Ver) 是两个签名方案, 我们所提出的基于身份的签名方案IBS 构造如下.

• Gen(1λ): 调用pp ← S.Setup(1λ), (vk,sk) ← S.KGen(pp), ˜pp ← ˜S.Setup(1λ), 置mvk :=(vk,pp, ˜pp), msk:=sk 并返回(mvk,msk).

• Ext(msk,id): 调用(˜vk, ˜sk)←˜S.KGen(˜pp), cert ←S.Sign(msk,id||˜vk), 并返回skid:=(˜vk, ˜sk,cert).

• Sign(skid,m): 将skid拆分为(˜vk, ˜sk,cert), 调用˜σ ←˜S.Sign(˜sk,m), 并返回签名σ :=(˜vk,cert,˜σ).

• Ver(mvk,id,m,σ): 将mvk 拆分为(vk,pp, ˜pp), σ 拆分为(˜vk,cert,˜σ), 如果S.Ver(vk,id||˜vk,cert)=1 且˜S.Ver(˜vk,m,˜σ)=1 则返回1, 否则返回0.

3.2 正确性与安全性

上述构造的IBS 的正确性源于其两个构造组件S 和˜S 的正确性.

IBS 的安全性依赖于S 的EUF-CMA 安全性和˜S 的MU-EUF-CMAcorr安全性, 且安全归约具有紧致特性, 参见定理1.

首先BS从他的EUF-CMA 实验的挑战者中获得S 的公开参数pp 与验证公钥vk, 挑战者同时还提供了一个签名预言机OSign(·), 其接收BS的输入m, 调用σ ←S.Sign(sk,m) 并返回σ. ˜S 部分由BS自己执行, BS调用 ˜pp ←˜S.Setup(1λ), 置mvk := (vk,pp, ˜pp), 并发送mvk 给敌手A. 这里BS隐式地设置msk 为sk. 针对A 的不同问询, BS做如下应答.

• 当A 进行OExt(id) 问询时, BS将id 存入集合Qid, 并检查是否存在(id,skid) ∈Qsk. 如果是则返回此skid; 否则BS调用(˜vk, ˜sk) ←˜S.KGen(˜pp), 向他自己的挑战者询问签名预言机获得关于id||˜vk 的签名cert, 将(id,skid:=(˜vk, ˜sk,cert)) 存入Qsk, 随后返回skid.

• 当A 进行OSign(id,m) 问询时, BS将(id,m) 存入集合Qm.

– 如果Qsk中存在一项(id,skid), BS将此skid拆分为(˜vk, ˜sk,cert), 调用˜σ ←˜S.Sign(˜sk,m), 并返回最终签名σ :=(˜vk,cert,˜σ).

综合公式(1), (2) 和(3), 定理1 得证.

4 通用构造的实例化

在本节中, 我们分别在随机预言机模型(random oracle model) 和标准模型(standard model) 下给出了紧致EUF-CMA 安全的签名方案S 和紧致MU-EUF-CMAcorr安全的签名方案˜S 的实例. 我们省略了算法细节部分, 仅保留方案所基于的安全假设与结论.

令GGen 表示一个群生成算法, 其输入安全参数1λ, 输出一个阶为q 的循环群G, 生成元为g, 即(G,q,g)←GGen(1λ).

定义6 (CDH 假设) 对于敌手A, 其解决计算型Diffie-Hellman 问题(CDH 问题) 的优势定义为

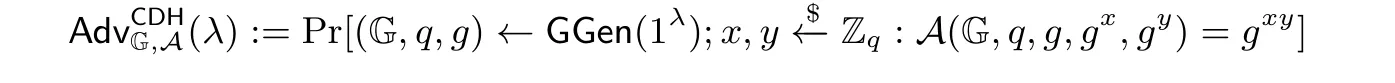
4.1 紧致EUF-CMA 安全的签名方案

4.1.1 随机预言机模型下的签名方案SDDH

4.1.2 标准模型下的签名方案SMDDH

Hofheinz 和Jager[4]利用树结构给出了一个紧致EUF-CMA 安全的签名方案, 其安全性基于DLIN假设. 他们的构造首先从一个保持代数结构的一次签名出发, 利用树结构先构造出非自适应安全的签名,随后再结合一次签名[22]构造出EUF-CMA 安全的签名方案. 随后,张等[7]将其思想扩展为到了MDDH假设上并构造出方案SMDDH, 算法详见文献[7].

4.2 紧致MU-EUF-CMAcorr 安全的签名方案

4.2.1 随机预言机模型下的签名方案˜SDDH

表1 基于DDH 假设的IBS 方案的比较Table 1 Comparison of IBS schemes based on DDH assumption

5 结束语

本文提出了第一个紧致EUF-CMA&CIA 安全的基于身份的签名方案, 其安全损失因子与敌手得到的签名数Q 及其涉及的用户数µ 无关. 方案构造用到了两个组件, 紧致EUF-CMA 安全的签名方案S, 和紧致MU-EUF-CMAcorr安全的签名方案˜S. 同时, 通过对两个组件进行实例化, 我们分别在随机预言机模型和标准模型下得到了紧致(与几乎紧致) 安全的基于身份的签名方案IBSDDH和IBSMDDH,其安全性分别基于DDH 假设和MDDH 假设. 我们这里的IBSMDDH方案基于双线性配对群, 而双线性映射计算开销大,效率低. 如何在标准模型下构造更高效的紧致安全IBS 方案仍是一个值得研究的问题.