关于Trivium-型序列密码代数次数估计的研究*
刘 晨, 田 甜
战略支援部队信息工程大学, 郑州450001
1 引言
序列密码是对称密码的分支之一, 用于对传输数据的加密. 序列密码的加密方式为密钥流比特与明文比特异或加, 其中密钥流由密钥和公开的初始化向量生成. 目前面向硬件实现的序列密码都采用基于非线性反馈移位寄存器(NFSR) 的设计, 例如Trivium[1]、Grain[2]等. Trivium 是由de Cannière 和Preneel 设计的面向硬件实现的序列密码, 是欧洲序列密码征集项目eSTREAM 计划的胜选算法之一. 并且, Trivium 已经成为轻量级序列密码算法的国际标准(ISO/IEC 29192-3:2012)[3]. Trivium 由一个二次非线性反馈移位寄存器和一个线性过滤函数构成, 因其设计结构简单, 受到国际学者的广泛关注. 到目前为止, Trivium 可以抵抗已有的所有攻击方法. 受Trivium 设计的启发, 一系列Trivium-型密码算法被提出, 主要包括Kreyvium[4]和TriviA-SC[5].
对于Trivium-型算法, 立方攻击(cube attacks)[6]是最有效的攻击方法. 立方攻击是由Dinur 和Shamir 在2009 年欧密会上提出的一种选择IV 攻击. 在立方攻击中, 将输出的密钥流比特看成是关于密钥变元k 和IV 变元v 的可调布尔函数f(k,v), 其核心思想是在选定的IV 取值集合上对函数f 的输出求和从而对f 的代数正规型进行简化, 得到低代数次数的密钥变元方程. 自从立方攻击思想提出以后, 得到了一系列的发展, 包括实验立方攻击[6–10]、相关立方攻击[11]以及基于可分性质的立方攻击[12–15]等.在实验立方攻击中, 攻击者主要通过随机检测的方法对超多项式进行线性和二次检测. 受限于立方变量的维数, 对于Trivium 算法, 实验立方攻击的最高轮数为802 轮[9]. 在相关立方攻击中[11], Liu 利用超多项式和一些简单密钥表达式之间的相关性给出了835-轮Trivium 的密钥恢复攻击. 2017 年美密会上由Todo 提出基于可分性的立方攻击, 受益于可分性和MILP 工具, 攻击者可以使用高维数的立方集, 这也进一步提高了立方攻击的效果. 例如, 在文[13] 中, 作者给出了891-轮Kreyvium 算法, 184-轮Grain-128a算法以及750-轮Acorn 算法的密钥恢复攻击.
另一方面, 在立方攻击中, 如果发现超多项式是零常值多项式, 则可以进行区分攻击, 区分攻击的轮数往往高于密钥恢复攻击. 常用的判断零常值多项式的方法是对立方变量在f(k,v)中的代数次数进行估计.对于指标集为I 的立方变量, 若变量集{vi|i ∈I} 在f(k,v) 中的代数次数小于|I|, 则以集合{vi|i ∈I}中变量为立方变量的超多项式是零常值. 对于高轮Trivium-型算法, 目前最有效的代数次数估计方法主要有Liu 提出的基于数值映射的方法[16]和Wang 等人给出的基于可分性的方法[13]. 基于数值映射的方法中, 利用数值映射的概念, 迭代计算每一个中间状态比特的代数次数上界. 该方法的优点是具有线性的时间复杂度和数据复杂度, 计算速度快. Wang 等人提出的基于可分性质的估计方法是在Todo 给出的MILP 模型[12]的基础上, 通过设置目标函数, 求解包含输入变元最多的项以估计布尔函数的代数次数.上述两种估计代数次数的方法除了寻找零和区分器, 在密钥恢复攻击中也有重要应用. 例如, 在相关立方攻击[11]中, 搜索基多项式主要依靠对超多项式进行代数次数估计, 基多项式是超多项式的一部分, 用来还原密钥信息; 在还原超多项式的代数方法中[14], 利用代数次数估计筛选有效立方集, 一个有效立方集的超多项式可以用代数的方法以概率1 还原; 在基于可分性的立方攻击中[13], 估计超多项式的代数次数可以更精确的评估立方攻击的理论复杂度.
针对Trivium-型算法, 本文对基于数值映射和基于可分性的两种代数次数估计方法进行了研究. 首先, 我们给出了对这两种方法优缺点的分析. 数值映射的效率高,但基于可分性的估计方法准确性相对更好. 通过将这两种方法结合, 我们给出一个改进算法: 利用可分性对Trivium-型算法低轮更新比特进行代数次数估计, 然后利用基于数值映射的方法迭代估计高轮输出比特的代数次数. 改进算法既可以基本保持数值映射的效率,也可以提高代数次数估计的准确性. 在Trivium-型的全变元条件下, 通过应用改进算法,我们将Trivium 算法未达到次数为160 的最大轮数下界从907 轮改进到了912 轮, 是目前已知的最优结果. 此外, 关于三个Trivium-型算法, 即Trivium、Kreyvium 和TriviA-SC, 我们对随机选择的固定维数立方集进行了代数次数估计的实验. 实验表明, 与数值映射相比, 改进后的算法能够给出更优的代数次数估计结果, 例如, 对于一个给定的立方集, 判断其是零和区分器的轮数可平均提高20 轮以上.
本文剩余部分结构安排如下: 第2 节为预备知识. 第3 节主要介绍了两种代数次数估计方法的优缺点, 并结合两种方法, 给出了本文估计代数次数的具体算法. 第4 节, 我们对Trivium-型算法进行了实际的估计, 并与之前的结果进行了对比. 第5 节对全文进行了总结.
2 预备知识
2.1 Trivium-型算法介绍
Trivium-型算法主寄存器部分为Galois 非线性反馈移位寄存器, 每个时刻有三个比特通过不同的二次反馈函数更新, 其它的中间状态比特则通过移位更新. 具体地, 令A,B,C 分别表示长度为nA,nB,nC的移位寄存器. 当时刻t ≥0 时, At= (xt,xt+1,··· ,xt+nA−1), Bt= (yt,yt+1,··· ,yt+nB−1), Ct=(zt,zt+1,··· ,zt+nC−1) 分别为寄存器A, B, C 在第t 时刻的状态, 且记第t 时刻Trivium-型算法的中间状态为s(t)=(At,Bt,Ct). 状态更新函数描述如下:
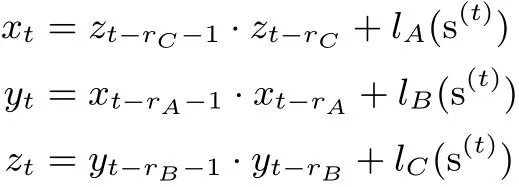
其中, lλ为线性函数, 且1 ≤rλ≤nλ, λ ∈{A, B, C}. 记f 为输出函数, 经过N 轮的初始化迭代之后,密码算法对每一个t ≥N 计算f(s(t)), 输出密钥流比特.
Trivium-型算法包含Trivium, Kreyvium 以及TriviA-SC, 且初始化轮数均为1152 轮. 其中, Trivium 支持80 比特密钥和80 比特IV; Kreyvium 是Trivium 的128 比特版本, 支持128 比特密钥和128比特IV; TriviA-SC 也支持128 比特密钥和128 比特IV. Kreyvium 除了三个寄存器A,B,C 以外, 还额外采用了两个寄存器K∗和V∗用来分别存储密钥KEY 和IV, 并以异或加的方式不断参与到反馈运算中. 此外, Trivium 和Kreyvium 的输出函数为线性布尔函数, 而TriviA-SC 的输出函数为二次布尔函数. 具体算法见附录B.
2.2 代数正规型与代数次数

其中wt(c) 为n 维向量c 的汉明重量, ac为ANF 的系数.
2.3 立方检测
设f ∈Bn, 给定指标集I = {i1,i2,··· ,i|I|} ⊂{1,2,··· ,n}, 并记tI= xi1xi2···xi|I|, 根据f 中的项是否能够被tI整除进行分类, 可以将f 唯一地表示为
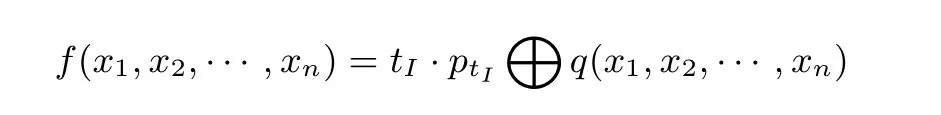
其中q 中的每一项都不是tI的倍式, ptI称为f 关于指标集I 的超多项式, 并称由指标集I 确定的变元集合CI= {xi1,xi2,··· ,xi|I|} 为立方变元集, xij∈CI称为一个立方变元. 遍历CI中变元所有2|I|种可能取值, 对函数f(x1,x2,··· ,xn) 求和可得

在序列密码分析中, 函数f(x1,x2,··· ,xn) 是输出比特关于密钥变元和IV 变元的布尔函数. 由于在初始化阶段经过了多轮非线性迭代, 函数f(x1,x2,··· ,xn) 的代数正规型是未知的, 从而超多项式的代数正规型也是未知的. 立方检测的基本思想是选取立方指标集I, 在遍历立方变元的所有可能取值以及非立方变元固定为常值的条件下, 对超多项式ptI的代数性质进行检测, 例如平衡性、代数次数、每个变元是否出现等, 从而能够使输出函数f 和随机函数进行区分. 特别地, 通过代数次数估计的方法可以判断零常值超多项式, 即若deg(f) < |I| 时, 则超多项式ptI一定是零常值多项式. 零常值多项式是概率1 成立的区分器, 也称为零和立方区分器.
2.4 基于比特的可分性与MILP 建模
基于比特的可分性 2015 年欧密会上, Todo 首次提出分组密码的可分性概念[17], 针对基于S 盒设计的分组密码, 描述了可分性质关于轮函数中一些基本运算的扩散规则, 从而由明文可分性质可以迭代求解密文的可分性质, 获得积分区分器. 2015 年, Todo 利用可分性质得到MISTY1 算法6 轮积分区分器[18],并给出MISTY1 首个全轮的理论攻击. 之后, 2016 年FSE 会议上, 针对基于比特运算设计的SIMON 算法, Todo 和Morii 进一步提出基于比特的可分性[19]. 基于比特的可分性定义如下:

2016 年亚密会上, Xiang 等首次将混合整数线性规划(MILP) 建模方法引入到轻量级分组密码可分路径的搜索[20], 大大提高了可分路径搜索的效率.
混合整数线性规划问题(MILP) 混合整数线性规划问题是通过建立整系数不等式方程组, 求解符合条件的最优整数解问题, 其中模型M 包含模型变量M.var, 模型限制条件M.con 以及模型的目标函数M.obj. 通过求解MILP 模型, MILP 将返回最优解或者无解; 若模型没有目标函数, 则只返回模型是否可解. 目前对于MILP 模型的求解, 主要依赖于Gurobi 和CPLEX 等求解器.
基于比特可分性的MILP 模型 在文[20] 中, Xiang 等将可分性关于copy, xor, and 的传播规则转化为MILP 模型, 利用MILP 求解器对模型进行求解. 若模型可解, 则可以得到满足条件的一条可分路径, 若模型无解, 则可以说明不存在满足条件的可分路径.
2017 年美密会上, Todo 首次将基于比特的可分性引入到了序列密码分析中, 并给出了可分性质在序列密码中的传播规则和MILP 建模, 具体参见文[12]. Todo 等人[12]给出了一个重要的引理, 见引理1.

通过引理1 可以得到文[12] 中的命题4. 基于引理1 和命题4, Todo 首次给出了基于可分性的立方攻击. 随后, 文[13] 对基于比特可分性的MILP 模型进行了改进. 特别地, flag 技术的提出使得攻击者能更准确的描述可分性的传播. 在flag 技术中, 通过对每个状态比特增加标识var.flag ∈{0c,1c,δ}, 分别标记状态比特为常值0、常值1 和变量δ, 并根据状态比特的标识修正可分性的传播. 标识var.flag 的运算规则如下:
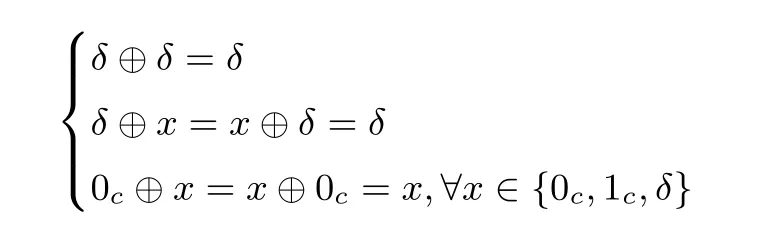
记改进的比特运算分别为copyf, xorf, andf, 此时其MILP 模型描述如下.

注1 性质3 中的限制条件存在冗余, 但并不妨碍得到正确的结果.
2.5 主要的代数次数估计方法
基于数值映射的代数次数估计 针对内部状态更新采用NFSR 的序列密码, 文[16] 提出了基于数值映射的代数次数估计方法, 并实际应用于Trivium-型序列密码, 对一些立方变元集得到了比较好的估计结果. 数值映射的定义描述如下:
定义2 (数值映射) 设f(x1,x2,··· ,xn)∈Bn为n 元布尔函数, 存在如下映射, 记为DEG:
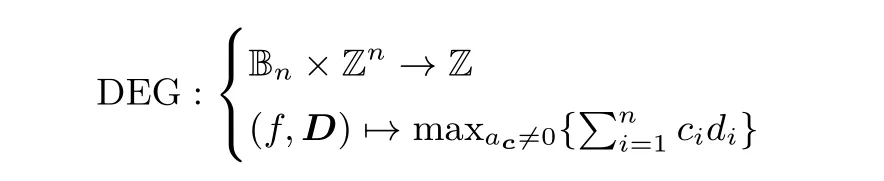
其中D =(d1,d2,··· ,dn)∈Zn为n 维向量, 且ac为上述f 的代数正规型的系数.
记G = (g1,g2,··· ,gn) 为n 元向量布尔函数, 并且令deg(G) = (deg(g1),deg (g2),··· ,deg (gn)),根据映射的性质易知

这表明通过数值映射估计的代数次数大于等于实际的代数次数, 并且容易证明下述性质4 成立.
性质4 若给定的n 维向量D =(d1,d2,··· ,dn) 满足deg (gi)≤di, 1 ≤i ≤n, 则有
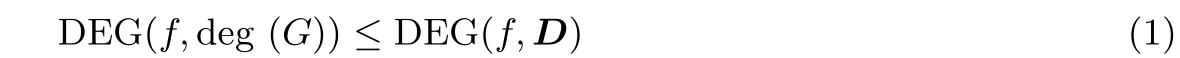
由性质4 可知, 利用数值映射估计的代数次数是实际代数次数的一个上界. 为了方便描述, 我们记复合函数h=f ◦G 的数值映射为DEG(h)∆=DEG(f,deg (G)).

基于可分性质的代数次数估计 Todo 等提出的基于可分性的立方攻击, 其核心思想是选择合适的指标集I, 在给定轮数下, 利用可分性确定输出比特的超多项式ptI中包含的密钥变元. 这些密钥变元构成集合J. 然后, 通过计算真值表恢复超多项式以建立代数方程组, 从而恢复密钥变元. 但是在实际攻击过程中, 该攻击受到指标集I 和集合J 大小的限制, 当|I|+|J| ≥n 时, 该攻击没有意义. 因此, 为了保证攻击的有效性, 文[12] 提出了关于立方攻击的两个假设, 但在Trivium-型算法初始化轮数较高时并不能验证其合理性. 为此, 在文[13] 中, Wang 等针对上述不足对基于可分性的立方攻击进行了改进. 在提出flag技术的同时, Wang 等将文[12] 中的命题4 进行了一般化的推广, 得到了命题1.

根据命题1, 针对Trivium-型序列密码, 文[13] 给出了建立带flag 技术的MILP 模型的算法Algorithm 4. 同时, 作者给出了基于可分性的估计代数次数的算法Algorithm 2, 将可分性质引入到了估计代数次数的问题中. 为了使Algorithm 2 能够对更新比特进行代数次数估计, 本文将Algorithm 4 中的限制语句进行了修改. 为了叙述的简洁, 本文约定用“可分性方法” 来简称“基于可分性质的代数次数估计的方法”, 且为了本文算法描述的简洁性, 记DegEval(I,r,flagλ) 为利用可分性方法对给定轮数r 的更新比特进行估计, 其中flagλ为更新比特的位置, I 为输入变元的指标集.
3 Trivium-型算法代数次数估计的改进
在本节中, 我们首先分析了数值映射方法和可分性方法这两种估计代数次数方法的优缺点, 并通过具体的实例展示了两种方法中存在的不足. 随后针对Trivium-型算法, 通过将这两种方法进行结合, 我们在3.2 节中给出了一个改进的估计代数次数的算法. 此外, 基于改进后的算法, 我们在3.3 节中给出了一个搜索零和区分器的算法.
3.1 两种代数次数估计方法的优缺点
针对同一加密算法, 两种方法各有优势, 同时也有一定的局限性. 相比于可分性方法, 线性的时间复杂度和存储复杂度是数值映射所具有的优势. 可以对给定立方集, 快速给出输出比特的次数上界, 且没有轮数的限制, 即使对初始化轮数较高的输出比特也能够快速给出估计. 但是利用数值映射对代数次数进行迭代估计时, 会产生以下几个问题, 以例1 为例.
例1 现设有4-bit NFSR, 其更新函数为f(x1,x2,x3,x4) = x1x2+x3x4, 记序列的初态为s(0)=(s0,s1,s2,s3), 并记第t 时刻的状态为s(t)= (st,st+1,st+2,st+3). 根据更新函数计算可得s4= s0s1+s2s3,s5=s1s2+s2s3+s0s1s3,s6=s2s3+(s0s1+s2s3)(s1s2+s2s3+s0s1s3)=s0s1s2+s0s1s3+s1s2s3.而利用数值映射对s6进行代数次数估计的结果为5.
通过例子可以看出, 估计结果偏高的原因为:
(1) 不能处理两个含有相同变元的项相乘时重复变元计数的问题. 例1 中, s4的两个单项式分别与s5中的最高次项s0s1s3有相同的变元s0和s1, 因此在实际计算时, 并不会出现5 次项, 但数值映射方法并不能处理这样的情况.
(2) 不能解决多项式中的消项问题. 计算过程中, s6的表达式中单项式s0s1s2s3出现了两次, 但数值映射方法同样无法解决这样的问题.
(3) 迭代导致的估计偏差的累积. 对s7进行估计时, 利用了s6的次数估计, 显然会使得估计结果继续偏高.
此外, 实际应用数值映射方法对Trivium-型算法进行代数次数估计时, 可以发现: 由于Trivium-型算法具有反馈函数二次项是相邻比特相乘的特点, 数值映射对于不包含相邻变量的情形估计效果很好, 对于含有相邻变量的情形估计效果较差, 例如在文[16] 中, 对于Trivium 算法, 作者检测了所有37 维到40 维不相邻的立方变量集. 而这一实验型现象主要是因为数值映射不能处理两个含有相同变元的项相乘时重复变元计数的问题.
可分性方法可以有效解决上述第1 个和第3 个问题. 因此相比于数值映射方法, 可分性方法给出的次数上界更紧. 但是可分性的传播规则和对MILP 模型的求解, 同样使得可分性方法存在以下两个问题:
(1) 不能解决多项式中的消项问题.
(2) 随着初始化轮数的增加, MILP 模型中的变元和限制条件大幅增加, 当初始化轮数较高时, 普通PC 机求解MILP 模型是困难的.
通过分析可以看出, 在初始化轮数较低时, 可分性方法能够给出比数值映射方法更加准确的次数上界;当初始化轮数较高时, 用可分性方法估计代数次数是困难的, 但此时数值映射方法可以快速给出较为准确的次数估计. 因此, 针对Trivium-型算法, 本文通过结合两种方法的优势, 能够对任意给定的立方集, 在初始化轮数较高的情况下, 给出比数值映射方法更加准确的结果.
3.2 对Trivium-型算法的代数次数估计
对于立方攻击以及与立方攻击相关的分析方法, 都需要进行大量的测试才能找到合适的立方集, 所以有效的时间内检测立方集的数量也是攻击成功的一个因素. 针对Trivium-型算法, 为了能够在有效时间内对初始化轮数较高的输出比特进行代数次数估计, 我们主要采用数值映射方法. 在实际估计过程中, 我们采用了文[16] 中提出的针对Trivium-型算法优化后的方法. 在该方法中, 对于i 时刻更新比特的次数上界是基于前nA+nC−3 个时刻更新比特的次数来进行估计的, 其中nA和nC分别是寄存器A 和寄存器C 的长度. 由于数值映射对估计偏差有累加的效果, 参见第3.1 节分析, 早期更新比特的代数次数上界估计越准确, 其最终的估计结果也就越准确. 值得注意的是, 基于可分性的估计方法能够给出更紧的次数上界. 同时, 当初始化轮数较低时, 可分性方法能够快速的给出更新比特的代数次数的上界. 因此, 为利用数值映射方法给出更紧的上界, 我们基于可分性方法对于早期的更新比特的代数次数上界进行了估计. 具体过程描述如下:
(1) 对给定的指标集I 确定多项式的变元, 并选取合适的l 和h, 使得t = l + h, 且满足k∆=l −(nC−2)−(nA−2)≥1;
(2) 利用可分性方法, 对从第k 时刻到第l 时刻的更新比特进行次数估计, 并保存结果;
(3) 将(2) 中所估计的代数次数用于数值映射的初始化, 并用数值映射方法对从l 时刻的更新比特进行估计, 最终给出输出比特s(N)out的次数上界.
现对具体的估计过程给出算法1.

算法1 代数次数估计Input: 给定轮数N; h; 指标集I;Output: s(N)out 的代数次数估计.1 endround ←h 2 startround ←endround −nA −nC +3 3 for t ←startround to endround do 4 for λ ∈{A,B,C} do λ ←DegEval(I,t,flagλ);6 end 7 end 8 D(endround)←(d(endround−nA+1)5 d(t)A ,···,d(endround)A ,d(endround−nB+1)B ,···,d(endround)B ,d(endround−nC+1)C ,··· ,d(endround)C );9 for t ←endround+1 to N do 10 for λ ∈{A,B,C} do λ ←max {DegMul(g(t)λ ),DEG(lλ,D(t−1))};12 end 13 D(t) ←(d(t−nA+1)11 d(t)A ,··· ,d(t)A ,d(t−nB+1)B ,··· ,d(t)B ,d(t−nC+1)C ,··· ,d(t)C );14 end 15 return DEG(f,D(N));
命题2 在给定指标集I, 轮数N, 参数h, 算法1 的输出为N-轮Trivium-型算法输出比特的一个代数次数上界.


其中s(t)为第t 时刻的中间状态, D(t)为由dλ构造的第t 时刻中间状态的代数次数. 又由数值映射的性质可知, 若给定的输入变元的代数次数大于等于实际代数次数, 则估计的输出比特的代数次数也大于等于实际次数. 综上, 算法1 给出的输出比特的代数次数一定为实际次数的上界.
命题2 可以保证, 算法1 能够用来估计给定指标集I 和初始化轮数为r 的Trivium-型算法的代数次数的上界. 并且可以看出, h 越大, 数值映射方法的初始化值就越准确, 迭代的轮数也越少, 但是所需时间就越长.
3.3 搜索给定指标集I 下的零和立方区分器
利用算法1 给出的代数次数上界,我们可以搜索给定指标集I 下的零和立方区分器. 具体见算法2. 通过分析算法1 可知, DEG(f,D(t)) 给出的值为t 时刻输出比特的代数次数上界. 因此, 算法2 能够保证, 在给定指标集I 下, Trivium-型算法在第maxround 轮一定存在关于该指标集I 的零和立方区分器.

算法2 给定指标集I 下的零和立方区分器搜索算法Input: 初始化轮数N; 轮数h; 指标集I Output: 给定指标集I 下, 能够构造的零和立方区分器的最大轮数maxround 1 endround ←h;2 maxround ←1;3 upperbound ←#I;4 startround ←endround −nA −nC +3;5 for t ←startround to endround do λ ←DegEval(I,t,flagλ);8 end 9 end 10 D(endround) ←(d(endround−nA+1)6 for λ ∈{A,B,C} do 7 d(t)A ,··· ,d(endround)A ,d(endround−nB+1)B ,··· ,d(endround)B ,d(endround−nC+1)C ,··· ,d(endround)C );11 for t ←endround+1 to N do 12 for λ ∈{A,B,C} do 13 d(t)λ ←max {DegMul(g(t)λ ),DEG(lλ,D(t−1))};14 end 15 D(t) ←(d(t−nA+1)A ,··· ,d(t)A ,d(t−nB+1)B ,··· ,d(t)B ,d(t−nC+1)C ,··· ,d(t)C );16 if DEG(f,D(t)) < upperbound then 17 maxround ←t −1;18 end 19 end 20 return maxround;
4 应用
4.1 Trivium-型算法全变元的代数次数估计
本节将IV 变元IV 和密钥变元KEY 均作为输入变元, 并利用本文方法对Trivium、Kreyvium和TriviA-SC 进行实验, 检测在全变元的条件下, Trivium-型算法在何时能够充分混合, 达到代数次数为#IV+#KEY. 虽然对于全变元条件下的代数次数估计结果不能直接用于攻击, 但其从代数次数的角度衡量了密钥变元和IV 变元在初始化迭代过程中混合的速度和程度, 对于评估算法的安全性具有一定意义.
根据文[16] 中的结果, 将Trivium 的160 比特变元作为输入变元, 其未达到代数次数为160 的最大轮数下界为907, 这也是目前最新的结果. 我们通过实验尝试, 最终选择l =601, 计算可得k =400, 即首先利用可分性方法对Trivium 的400 到601 轮的更新比特进行代数次数估计. 利用算法2, 我们给出的下界为912. 与数值映射方法给出的结果相比, 我们对代数次数的估计更精确. 算法2 在利用了可分性优势的同时, 保证了代数次数估计的效率. 由于所需时间太长, 可分性估计方法无法对全变元的代数次数进行估计, 目前也没有关于可分性对全变元进行代数次数估计的公开结果.
类似地, 我们还对Kreyvium 和TriviA-SC(v2) 进行了实验, 现将实验结果展示在表1 中.

表1 Trivium-型算法在KEY 和IV 全变元条件下未达到代数次数为#KEY+#IV 的最大轮数下界Table 1 A lower bound for the maximum number of rounds of not achieving the algebraic degree # KEY+# IV for Trivium-like ciphers with all KEY and IV variables
4.2 关于Trivium 代数次数估计结果
针对Trivium 算法, 本节对算法2 和数值映射的估计结果进行了比较.
首先, 测试了随机选择的100 组48 维立方集CI. 将48 比特的立方变元作为更新函数和输出函数的输入变元, 利用算法2, 我们在给定立方集下, 给出了零和立方区分器能够达到的最高轮数的估计. 同时,我们对实验结果进行统计, 并与数值映射方法进行了对比, 具体结果参见表2.

表2 关于100 组48 维立方集, 算法2 与数值映射方法关于Trivium 估计结果的比较Table 2 Comparison of Algorithm 2 and numeric mapping method for Trivium under 100 cubes of dimension 48
从表2 可以看出, 对任意给定的立方集, 算法2 对代数次数的估计更加准确, 所得零和立方区分器的轮数更高, 平均能够提高33 轮, 最高能够提高52 轮(具体立方集见附录A). 在实际估计过程中, 与可分性方法相比, 本节使用的方法速度更快, 能够对更多的立方集进行估计.
其次, 测试了随机选择的100 组39 维的立方集, 利用算法2 对其进行实验检测. 同样, 我们将所得结果与数值映射方法的结果进行了对比, 具体结果参见表3.

表3 关于100 组39 维立方集, 算法2 相较于数值映射方法的提升效果Table 3 Comparison of Algorithm 2 and numeric mapping method for Trivium under 100 cubes of dimension 39
从表3 可以看出, 对随机选取的100 个39 维立方集, 算法2 同样能够给出更优的零和立方区分器, 平均提高36 轮, 最多提高58 轮(见附录A), 并且在随机实验中, 最高给出了821 轮的零和区分器.
4.3 关于Kreyvium 代数次数估计结果
针对Kreyvium 算法, 本节随机选取了100 组72 维的立方集. 将72 比特立方变元作为更新函数和输出函数的输入变元, 并利用算法2, 在给定立方集下对零和区分器能够达到的最高轮数进行估计, 并与数值映射方法进行比较. 统计结果如表4 所示.

表4 算法2 与数值映射方法关于Kreyvium 估计结果的比较Table 4 Comparison of Algorithm 2 and numeric mapping method for Kreyvium
通过实验统计结果可以看出, 在给定立方集下, 对于Kreyvium, 算法2 同样能够给出比数值映射方法更准确的次数估计, 找到更高轮数的零和区分器. 其中, 最大轮数的零和区分器为844 轮, 平均能够提高22 轮, 且提升轮数最高的为39 (见附录A). 但由于Kreyvium 算法结构的原因, 在使用可分性方法对其400 到601 轮更新比特进行代数次数估计时, 所需时间较长. 尽管如此, 所需时间依旧远少于可分性方法.
4.4 关于TriviA-SC 代数次数估计结果
针对TRIVIA-SC(v2) 算法, 本文同样随机选取了100 组72 维的立方集, 利用算法2 估计零和区分器的最大轮数, 与数值映射方法的比较见表5.

表5 算法2 与数值映射方法关于Kreyvium 估计结果的比较Table 5 Comparison of Algorithm 2 and numeric mapping method for Kreyvium
由表5 结果可以看出, 算法2 同样给出了TriviA-SC(v2) 更优的零和区分器, 在随机情况下能够找到的最高轮数为914, 并且与数值映射方法相比, 平均提升的轮数为20 轮, 其中提升轮数最多的为37 轮(见附录A). 因此, 相比于数值映射方法, 算法2 搜索零和区分器的能力更强. 同时, 尽管与Kreyvium 相比,TriviA-SC(v2) 使用了更长的中间状态, 但是在同样72 维的条件下, 利用可分性方法对TriviA-SC(v2) 前期更新比特进行代数次数估计时, 所需时间少于Kreyvium.
5 结论
对于Trivium-型算法的代数次数估计, 目前最有效的两个方法分别是数值映射方法和可分性方法. 本文主要通过分析两种估计方法的优势和劣势, 对Trivium-型算法的代数次数估计方法进行了改进: 利用可分性方法对低轮数内部状态的代数次数进行了估计, 作为数值映射的初始化值. 在本文中, 我们对随机选取的立方集进行了实验. 实验结果表明: 与数值映射方法相比, 改进后的方法给出的零和区分器轮数更高;而且与可分性相比, 改进后的方法效率更高. 因此, 改进后的方法能够对更多维数更高的立方集进行搜索,在随机情况下, 更容易找到高轮数的零和区分器. 特别地, 对Trivium-型算法全变元的情形, 利用改进后的方法, 我们给出了优于数值映射的新结果. 虽然本文使用的方法实际是对数值映射和可分性方法的折中,但对于在立方攻击中提高大维数立方超多项式代数次数估计的效率仍有一定的意义.

