LowMC实例的差分枚举攻击效果分析

葛欣欣，李智虎，王美琴，胡凯

LowMC实例的差分枚举攻击效果分析

葛欣欣1,2，李智虎3，王美琴1,2，胡凯1,2

（1. 山东大学网络空间安全学院（研究院），山东 青岛 266237；2. 山东大学密码技术和信息安全教育部重点实验室，山东 青岛 266237；3. 中国电力科学研究院有限公司，北京 100192）

LowMC是具有低乘法复杂度特征的算法。针对低数据量和少量S盒参数下的LowMC实例，差分枚举攻击被提出，理论上可以攻击全轮LowMC算法。考虑到这种攻击是在线性层完全随机的条件下给出的，对LowMC算法在真实的线性层下抵抗差分枚举攻击的强度进行了研究。通过对关键起始轮数的研究发现，差分枚举攻击并非总是可以达到理论攻击轮数。对于某一些关键起始轮数比理论值小的LowMC实例，差分枚举攻击甚至会失败。由于LowMC算法的轮数设置基于现有攻击的效果，该分析对LowMC算法的轮数设计具有重要意义。

分组密码；LowMC算法；差分枚举攻击；关键起始轮数

1 引言

Albrecht等[1]在2015年欧密会上提出了LowMC算法。LowMC算法基于SPN结构，采用了部分非线性层和随机线性层的设计，其乘法复杂度非常低。LowMC实例是通过改变分组长度、密钥长度、每轮S盒的数量和数据复杂度的安全预期得到的。LowMC算法的低乘法复杂度特点使它在多方计算和全同态加密等场景下效率较高，自公开以后就受到了广泛关注。

本文研究了差分枚举攻击对实例化后的LowMCv2算法的攻击效果，发现对于某些参数的LowMC实例，差分枚举攻击的实际可攻击轮数并不能达到理论计算值。差分枚举攻击的可攻击轮数与LowMCv2算法的概率为1的差分路线（这条路线的轮数被称为关键起始轮数）直接相关。为此，本文给出一种高效的计算LowMC算法概率为1的差分路线的方法。本文控制非线性层部分的差分状态，保证S盒部分不引入差分、其他部分引入差分，建立差分传播的线性方程组。之后通过高斯消元法[10]解方程组，可以得到概率为1的差分路线。实验发现，无论是在LowMC算法设计者推荐的线性矩阵下，还是任意随机矩阵下，关键起始轮数都有很大概率无法达到理论值，也就是说，差分枚举攻击并不总是可以达到理论的攻击轮数。对于某些特殊参数下的LowMC算法实例，差分枚举攻击甚至会失败。在LowMCv3算法中，考虑了差分枚举攻击的可攻击轮数，重新定义LowMC算法的轮数。本文对差分枚举攻击的实际攻击效果分析表明，LowMCv3算法的轮数可以适当降低，以提升LowMCv3算法的实现效率。

2 差分枚举攻击及在LowMC算法的应用

2.1 LowMC算法描述

由个3 bit S盒组成。非线性层中采用了具有低代数次数、低乘法复杂度等特点的S盒，S盒为 。此时要求和的关系满足，当时，剩余的位状态直接进入线性层。

Figure 1 The round function of LowMC

LowMC算法的分组长度、密钥长度、每轮S盒的数量和可承受攻击的数据复杂度是可以根据应用场合改变的参数，被称为可变参数。为了适用于多种应用场合，可变参数调整得到不同的实例。对于不同的实例，LowMC算法轮数是根据可变参数现存的有效攻击计算得到的，所以正确分析每个攻击的可攻击轮数，对于LowMC算法来说至关重要。LowMC算法线性层的特点是随机选取且相互独立的。在保证随机性、可靠性、快速生成有效随机位的前提下，设计者推荐用Grain算法中的线性反馈移位寄存器（LFSR, linear feedback shift register）[11]作为自收缩发生器[12]生成线性层，预期这样可以得到尽可能随机化的线性层。考虑到使用LFSR生成的线性矩阵存储空间和计算消耗比较大，将线性层优化为等价线性层[13]可以在不增加非线性操作和不危及安全性的同时，减少线性代数复杂度。

2.2 差分枚举攻击在LowMC算法上的应用

定义2 关键起始轮数。

关键起始轮数定义为，在部分非线性层中，通过选择合适的输入差分，得到传播概率为1的差分路线的长度。

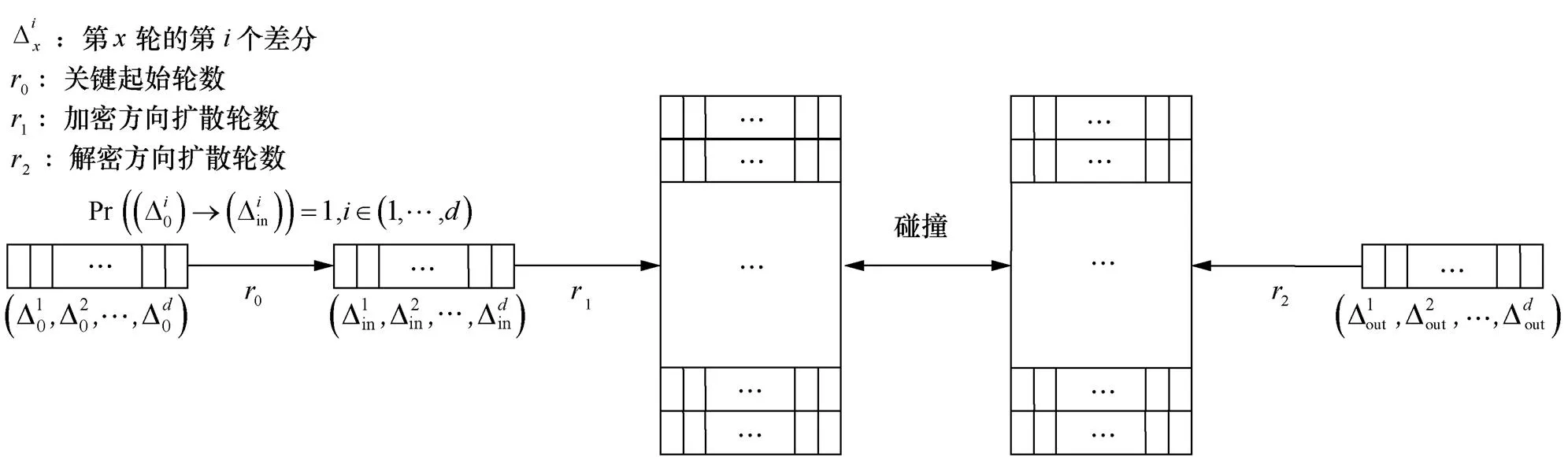
图2 差分枚举在LowMC算法上的应用

Figure 2 Application of difference enumeration in LowMC

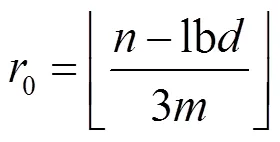
3 差分枚举攻击对线性层实例化后的LowMC算法的攻击效果分析

在对LowMC算法实施差分枚举攻击时，部分非线性层的特性导致攻击可以分为两部分，第一部分是概率为1的关键起始轮数，第二部分是具有差分概率的差分扩散轮数。为了保证可攻击的轮数最大，或者以最小的时间复杂度攻击全轮数，关键起始轮数一定要取到最大值。线性层作为提供扩散性的组件，不仅影响密码算法实现效率，也影响密码算法安全性[16]。在具体线性层下，实际的关键起始轮数有可能无法达到理论值，因此造成差分枚举攻击达不到理论的攻击轮数。对于某些参数下的LowMC算法实例，甚至会攻击失败。

3.1 差分枚举攻击在特定线性层下的关键起始轮数

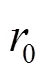
步骤2 利用高斯消元法求解线性方程组，并对自由变量进行遍历，得到符合条件的非零差分路线。

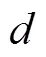
实例1 Grain算法中的LFSR作为自收缩发生器生成线性层。

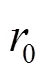
实例2 2019年欧密会提出的LowMC算法的线性层。

LowMC算法为了减少乘法复杂度，采用了部分非线性层的设计，同时为了弥补部分非线性层带来的混淆不充分，采用了高代数次数的随机矩阵为线性层增强扩散度，这给LowMC算法的实现带来了负担。Dinur等[13]在2019年欧密会上提出在每个LowMC实例等价类中存在线性等价性，可以在每个实例类中得到一个最优线性层，并伴随着加解密算法的优化。针对这种优化下的线性层，本文进行了4差分下的关键起始轮数是否可达到理论值的判断，结果是在4差分下不可达到理论的42轮关键起始轮数，实际关键起始轮数为41轮。等价线性层在4差分下不可达到理论关键起始轮数的这一结果和对Grain算法中LFSR生成的线性层测试得到的结果一致。

实例3 真随机数生成的LowMC算法线性层。

本文使用C++语言中的random_device真随机数生成库，验证随机生成的线性矩阵的实际关键起始轮数是否和其他特定选取算法下生成的线性矩阵的实际关键起始轮数相同。利用随机数生成器生成20 000组LowMC实例的42轮线性矩阵，计算关键起始轮数可以达到42轮的差分路线个数，实验结果见表1。由表1可知，使差分路线个数达到7条的线性矩阵有4 416组，占总数的22.08%；使差分路线个数达到15条以上的线性矩阵有233组，占总数的1.17%；剩余的线性矩阵使差分路线个数为3条，占总数的76.75%，即随机选取线性矩阵只有23.25%的概率可达到4差分理论关键起始轮数42轮。

利用上述计算实际关键起始轮数的步骤1～步骤4，可以计算实际关键起始轮数，从而确定非零差分路线个数和实际关键起始轮数的联系。随机选取3 000次LowMC线性矩阵，计算4差分下的最长关键起始轮数，实验结果见表2。实际关键起始轮数等于理论关键起始轮数的线性矩阵有721次，概率为24.03%，所占比例与上面7条差分路线个数的比例基本相同；不可达到理论关键起始轮数的线性矩阵有2 277次，所占比例为75.9%，此外，实际关键起始轮数大于理论关键起始轮数的线性矩阵有2次，所占比例可忽略不计。由此，可以认为在线性矩阵下，实际关键起始轮数的差分路线个数为7条及以上时，可攻击轮数与理论关键起始轮数相等；小于7条时，不可达到理论关键起始轮数。

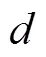
表1 随机线性矩阵下的满足理论关键起始轮数的差分路线数量注1

注1：线性矩阵由random_device库生成，分组长度为128 bit，每轮1个S盒，差分维度为4，理论关键起始轮数为42轮。

表2 随机线性矩阵下的实际关键起始轮数注1

3.2 LowMC算法轮数设置分析

为了确定保证LowMC算法安全性下的最低轮数，对大部分标准攻击进行评估，得到第二版建议轮数。

LowMC算法的分组长度、密钥长度、每轮S盒数量等参数是可变的，不同参数的加密算法特征和适用范围有所不同。特别地，令每轮S盒数量和数据量都取较小值，这种少量S盒、低数据量参数下的LowMC实例可用于非交互式零知识证明的公钥签名方案的加密算法。针对这种参数下的LowMC实例提出的差分枚举攻击影响了第三版轮数的计算。经过LowMCv2算法轮数和差分枚举攻击轮数计算，由Grain算法的LFSR生成线性矩阵，以128 bit分组长度、1个S盒、差分维度取4为例，得到理论上不可抵抗差分枚举攻击，而实际可抵抗差分枚举攻击的参数见表3。由此实例可见，在实际的差分枚举攻击下，差分枚举攻击可能会失败。为了抵抗差分枚举攻击，第三版LowMC算法（LowMCv3）更改了轮数计算方法。LowMCv3算法的轮数为差分攻击、线性攻击、飞去来器攻击、插值攻击、差分枚举攻击等一系列攻击的最大轮数。由上述分析结果可知，在特定参数类型的部分LowMC实例下，差分枚举攻击并不总是可以达到理论攻击轮数，因此，针对此类参数，LowMCv3算法的轮数可以适当降低，进一步提升实现效率。

表3 理论与实际差分枚举攻击对比注2

注2：线性矩阵由Grain算法的LFSR生成，分组长度为128 bit，1个S盒，差分维度为4。

4 结束语

本文主要对少量S盒、低数据量参数下的LowMC实例的差分枚举攻击效果进行分析，利用高斯消元法对加密过程中构建的线性方程组进行求解，得到差分枚举攻击的实际关键起始轮数。实验结果表明，对于某些LowMC算法实例，实际关键起始轮数往往小于其理论值。实际和理论的关键起始轮数的差异导致差分枚举攻击的实际攻击效果达不到预期，通过改变LowMC算法的线性层，可以得到多个LowMC算法的实例。这些实例中，仅有23.25%的实例可以被差分枚举攻击成功攻破。对于剩余的LowMC实例，差分枚举攻击必须通过减少差分维度或关键起始轮数来保证攻击可行性。由于LowMCv3部分实例的轮数主要考虑了差分枚举攻击的效果，这部分LowMCv3算法的实例可以适当减少轮数以提升实现效率。

[1] ALBRECHT M R, RECHBERGER C, SCHNEIDER T, et al. Ciphers for MPC and FHE[C]//EUROCRYPT. 2015: 430-454.

[2] DINUR I, LIU Y W, MEIER W, et al. Optimized interpolation attacks on LowMC[C]//ASIACRYPT. 2015: 535-560.

[3] DOBRAUNIG C, EICHLSEDER M, MENDEL F. Higher-order cryptanalysis of LowMC[C]//ICISC. 2015: 87-101.

[4] CHASE M, DERLER D, GOLDFEDER S, et al. Post-quantum zero-knowledge and signatures from symmetric-key primitives[C]// ACM Conference on Computer and Communications Security. 2017.

[5] RECHBERGER C, SOLEIMANY H, TIESSEN T. Cryptanalysis of low-data instances of full LowMCv2[C]//IACR Trans Symmetric Cryptol. 2018: 163-181.

[6] DEMIRCI H, SELÇUK A A. A meet-in-the-middle attack on 8-round AES[C]//FSE. 2008: 116-126.

[7] DUNKELMAN O, KELLER N, SHAMIR A. Improved single-key attacks on 8-round AES-192 and AES-256[C]//ASIACRYPT. 2010: 158-176.

[8] 陈少真, 鲁林真. 对8轮ARIA算法的差分枚举攻击[J]. 电子与信息学报, 2011, 33(7): 1770-1774.

CHEN S Z, LU L Z. Differential enumeration attack on ARIA[J]. Journal of Electronics and Information Technology, 2011, 33(7): 1770-1774.

[9] 崔竞一. 基于中间相遇思想的攻击方法研究[D]. 郑州: 信息工程大学, 2017.

CUI J Y. Research on cryptanalysis based on meet-in-the-middle[D]. Zhengzhou: Information Engineering University, 2017.

[10] 王萼芳, 石明生. 高等代数(第三版)[M]. 北京: 高等教育出版社, 2003.

WANG E F, SHI M S. Advanced algebra (third edition)[M]. Beijing: Higher Education Press, 2003.

[11] HELL M, OHANSSON T, MAXIMOV A, et al. The grain family of stream ciphers[J]. The eSTREAM Finalists, 2008: 179-190.

[12] MEIER W, STAFFELBACH O. The self-shrinking generaTor[C]//EUROCRYPT. 1994: 205-214.

[13] DINUR I, KALES D, PROMITZER A, et al. Linear equivalence of block ciphers with partial non-linear layers: application to LowMC[C]//EUROCRYPT. 2019: 343-372.

[14] TIESSEN T. Polytopic cryptanalysis[C]//EUROCRYPT. 2016: 214-239.

[15] NYBERG K. Differentially uniform mappings for cryptography[C]//EUROCRYPT. 1993: 55-64

[16] 李鹏飞. 基于密码结构的扩散层构造[J]. 网络与信息安全学报, 2017, 3(6): 65-76.

LI P F. Construction of diffusion layers based on cipher structures[J]. Chinese Journal of Network and Information Security, 2017, 3(6): 65-76.

Effect of the difference enumeration attack on LowMC instances

GEXinxin1,2, LI Zhihu3, WANGMeiqin1,2, HU Kai1,2

1.School of Cyber Science and Technology, Shandong University, Qingdao 266237, China 2. Key Laboratory of Cryptologic Technology and Information Security, Ministry of Education, Shandong University, Qingdao 266237, China 3.China Electric Power Research Institute, Beijing 100192, China

The LowMC is an algorithm with low multiplicative complexities. For the parameter with limited data complexities and low number of S-boxes, the difference enumeration attack was proposed, which could theoretically attack all rounds of the LowMC. Considering that the original attack is based on the random linear layer,the strength of LowMC algorithm against differential enumeration attacks under a specific linear layer deserves more study. The difference enumeration attack cannot reach theoretical rounds through the research on the so-called key initial round. In terms of some LowMC instances, the key initial round is smaller than the theoretical value, which leads to the failure of the difference enumeration attack. Since the number of rounds of the LowMC is completely based on existing attacks, the analysis is of great significance to the rounds design of the LowMC.

block cipher, LowMC algorithm, difference enumeration attack, key initial round

TN918.1

A

10.11959/j.issn.2096−109x.2021046

2021−01−10；

2021−03−15

王美琴，mqwang@sdu.edu.cn

国家自然科学基金（62002201，62032014）；国家重点研发计划（2018YFA0704702）；山东省重大科技创新项目（2019JZZY010133）；山东省自然科学基金重大基础研究项目（ZR202010220025）

The National Natural Science Foundation of China (62002201, 62032014), The National Key R&D Program of China (2018YFA0704702), The Major Scientific and Technological Innovation Project of Shandong Province (2019JZZY010133), The Major Basic Research Project of Natural Science Foundation of Shandong Province, (ZR202010220025)

葛欣欣, 李智虎, 王美琴, 等. LowMC实例的差分枚举攻击效果分析[J]. 网络与信息安全学报, 2021, 7(3):149-155.

GE X X, LI Z H, WANG M Q, et al. Effect of the difference enumeration attack on lowMC instances[J]. Chinese Journal of Network and Information Security, 2021, 7(3): 149-155.

葛欣欣（1997− ），女，吉林四平人，山东大学硕士生，主要研究方向为分组密码分析。

李智虎（1975− ），男，安徽望江人，中国电力科学研究院有限公司高级工程师，主要研究方向为密码理论和密码工程。

王美琴（1974− ），女，宁夏银川人，山东大学教授、博士生导师，主要研究方向为对称密码算法的设计和分析。

胡凯（1992− ），男，山东临沂人，山东大学博士生，主要研究方向为对称密码的分析。