对“以考促学”提升数学应用能力的几点认识

房胜

[摘  要] 高中数学知识在生活中有着广泛的应用，但在“唯分论”的影响下，教学中对学生应用意识和应用能力的培养未引起足够的重视. 随着新课改的不断深入，高考也加强了对学生应用意识的考核，从而通过“考”刺激“学”，以达到“学以致用”的目的.

[关键词] 应用意识;应用能力;学以致用

在传统的教育思想及“唯分论”的教学评价模式的影响下，高中数学课堂上更关注对解题方法和解题技巧的培训，对数学知识的来源、生成过程和应用方法常视而不见，从而造成学生数学应用意识薄弱. 然而数学的应用范围广泛，如果只关心学生是否可以正确解答考题，而忽视对应用意识和应用价值的培养，使得学生在遇到实际问题时无法运用数学知识去解答，那么无法实现“学以致用”的目的.

在素质教育的影响下，教学方向及教学方法都有了质的发展，数学应用意识的培养也逐渐得到了关注. 笔者选择了几个高考重点考查的题型，以期与同行一起探讨，并引起师生对数学应用意识的重视.

[⇩] 函数

函数的学习贯穿于整个高中数学，其不仅是高考的必考考点，而且其在现实生活中的应用也是随处可见. 例如，生活中“最便宜”“最合适”“最短”等相关的最值问题常用函数进行求解，因此其重要性是不言而喻的. 为了提升学生的函数应用意识，常通过“以考促学”的形式来强化学生的函数建模意识和建模能力.

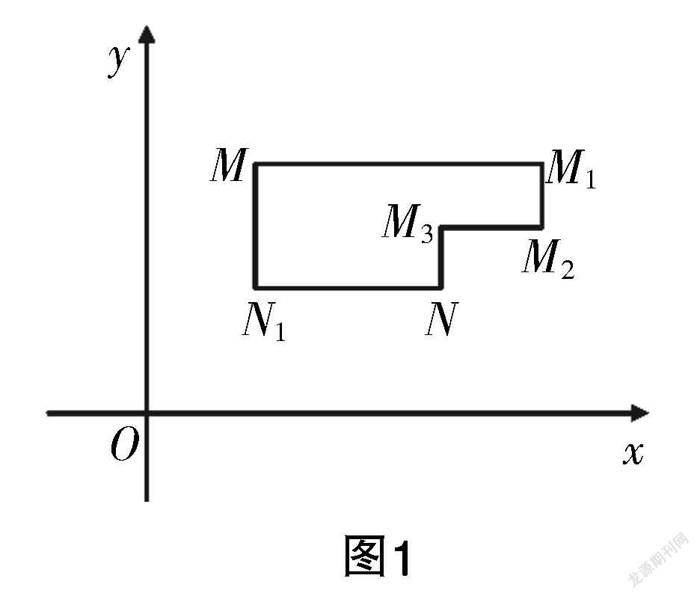
例1 在平面直角坐标系xOy中，将从点M出发沿水平和垂直方向到达点N的任意一条路径称为“L路径”. 如图1所示，路径MMMMN和路径MNN都是点M到点N的“L路径”. 某地新建了3处住宅楼，在平面直角坐标系xOy内3点的坐标分别为A（3，20），B（-10，0），C（14，0）. 现计划选择一点P修建一个文化中心，点P的位置要设置于x轴上方或x轴上.

（1）写出点P到住宅楼A的“L路径”的长度最小值表达式;

（2）若以原点O为圆心，r=1的圆内不允许建立文化中心，即“L路径”不能进入保护区，现确定点P的位置，使其到3个住宅楼的“L路径”长度相加值最小.

题目解析：求第（2）问时，因为存在保护区，所以确定点P的位置（即求点P的坐标）需要分类讨论.

设点P的坐标为（x，y），定点P到3个住宅楼的“L路径”长度相加值最小为d，则

（1）点P到住宅楼A的“L路径”的长度最小值为x-3+y-20，y∈[0，+∞）.

（2）由题意可知，可将问题转化为“点P到3個住宅楼的‘L路径’的距离之和的最小值”.

①当y≥1时，d=x+10+x-14+x-3+2y+y-20. 因为d（x）=x+10+x-14+x-3≥x+10+x-14≥24，所以当且仅当x=3时，d（x）的最小值为24. 因为d（y）=2y+y-20≥21，所以当且仅当y=1时，d（y）的最小值为21. 所以点P的坐标为（3，1）时，其长度相加值最小，最小值为45.

②当0≤y≤1时，“L路径”不能进入保护区，所以d（x）=x+10+x-14+x-3，d（y）=1+1-y+y+y-20=22-y≥21. 由①知d（x）≥24，所以d（x）+d（y）≥45，当且仅当x=3，y=1时恒成立.

因此，求得点P的坐标为（3，1）.

反思：本题是非常具有应用价值的题目，充分地考查了学生的函数建模能力，并巧妙地应用了绝对值的几何意义，分类讨论思想更加体现了思维的严谨性.

[⇩] 导数

导数与函数、不等式、数列、解析几何等知识点都有着密切的联系，其可谓是高中数学知识的一个交汇点，因此导数在数学中的应用意义是不可估量的.

例如，在高中数学引入导数后，方便了学生更好地理解函数的性质——对于基本初等函数可以通过函数的图像清晰地表达函数的定义域、值域等基本性质，但是对于非基本初等函数却很难利用图像准确表达，而学习导数后就可以轻松地通过求导来判断函数的极值点、最值点、拐点等，将复杂的问题简单化，方便了学生对函数性质的理解. 另外，其有利于培养学生的函数思想，有利于学生理解曲线的切线方程，有利于发展学生的思维能力，且对其他学科的学习也发挥着巨大的作用. 因此，若要提高学生的数学应用能力，则要充分发挥导数的工具性和应用性的作用，从而为学生解决问题带来新思路，为数学学习带来新活力.

例2 已知函数f（x）=x2+ax+b，g（x）=ex（cx+d）. 若两曲线f（x）与g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2.

（1）求a，b，c，d的值;

（2）若x≥-2时，f（x）≤kg（x），求k的取值范围.

题目解析：（1）由题意可知，f（0）=2，g（0）=2，f′（0）=4，g′（0）=4，得a=4，b=c=d=2.

（2）f（x）=x2+4x+2，g（x）=2ex（x+1）. 设h（x）=kg（x）-f（x）=2kex（x+1）-x2-4x-2. 对h（x）求导，即h′（x）=2（x+2）（kex-1）. 由题意得h（x）≥0，即k≥1. 令h′（x）=0，得x=-lnk，x=-2.

①若1≤k≤e2，则-2≤x≤0，从而当x∈（-2，x）时，h′（x）<0;当x∈（x，+∞）时，h′（x）>0.即h（x）在（-2，x）上单调递减，在（x，+∞）上单调递增，故h（x）在[-2，+∞）上的最小值为h（x）. 而h（x）= -x（x+2）≥0，故当x≥-2时，h（x）≥0，即f（x）≤kg（x）恒成立.

②若k>e2，则h（-2）=+2<0，所以当k>e2，x≥-2时，f（x）≤kg（x）不可能恒成立.

综上可知，k的取值范围是[1，e2].

反思：本题主要是导数在研究曲线的切线方程中的应用，通过对函数的恒成立问题的研究，使学生深入理解了导数在函数学习中的应用价值，从而不仅强化了导数的应用，也使得学生加深了对函数性质的认识，有效地拓展了学生的知识面.

[⇩] 数列

导数是数学知识的一个交汇点，数列也有着同样的地位，其与方程、函数、不等式等内容也息息相关，是高考的主要考查内容之一. 数列问题一般新颖多变，可以多角度、多层次地考查学生的数学应用能力，因此也是教学的重难点. 为了让学生学好数列，靠单纯的“题海战术”显然是无法解决的，应注重学生数学分析能力的培养，关注问题的本质属性，让学生掌握解决此类问题的通性通法，从而培养学生的应用意识.

例3 阅读给出的线性数列的定义及定理解决问题.

定义：对于给定数列{x}，若满足x=px+q（p，q为实常数）对于任意n∈N*都成立，就称数列{x}为线性数列.

定理：若线性数列{x}满足x=px+q，其中p，q为实常数，且p≠1，q≠0，则数列

x-

是以p为公比的等比数列.

（1）如果a=2n，b=3·2n，n∈N*，根据定义是否可以判断数列{a}，{b}为线性数列？若可以，请求出对应的实常数p，q;若不可以，请说明理由.

（2）若数列{c}的前n项和为S，且对任意的n∈N*，都有S=2c-3n.

①请根据定义证明数列{c}为线性数列;

②请应用定理，求数列{c}的通项公式;

③求数列{c}的前n项和S.

题目解析：求解第（1）问时，只要根据给出的线性数列的定义逐个进行判断即可，从而得到a=a+2，b=2b.

（2）令n=1，则S=2c-3，所以c=3. 又n≥2（n∈N*）时，S=2c-3（n+1），S=2c-3n. 将两式相减，得c=2c-2c-3，则c=2c+3，n=1时也成立，所以c=2c+3，n∈N*. 故数列{c}为线性数列，其对应的实常数为p=2，q=3. 因此{c+3}是公比为2的等比數列，所以c+3=（c+3）·2n-1，所以c=6·2n-1-3，从而S=6（1+2+22+…+2n-1）-3n=6·2n-3n-6.

反思：本题设计思路新颖，利用给出的定义和定理，让学生学会分析和掌握定义和定理的本质，从而在解决问题时利用其属性构建认知体系. 虽然定义和定理是新内容，但学生对数列的基本解题方法和解题技巧有着深刻的认识，因此求数列的通项公式及数列的前n项和时，显得游刃有余. 总之，无论题目多么新颖多变，只要有着扎实的基础和过硬的心理素质，问题都会迎刃而解.

[⇩] 解析几何

解析几何是架设于代数与几何之间的桥梁，其有效地融合了代数、几何、函数等相关知识，更使数形结合思想得到了发展. 在高中阶段，解析几何的题目主要是以直线和二次曲线为核心的研究内容，通过整体代换、数形结合等解题技巧来体现其在数学中的应用价值.

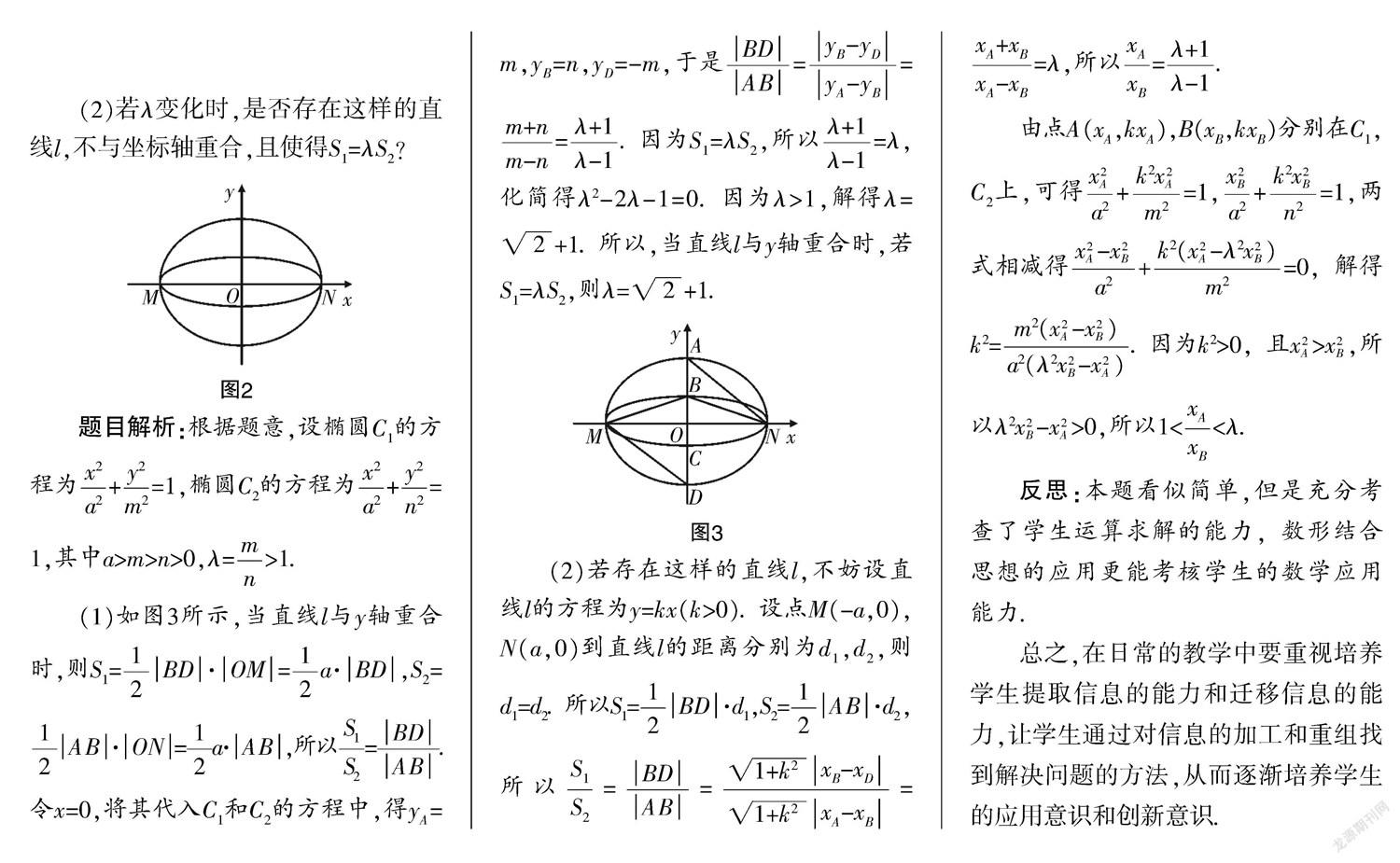
例4 如图2所示，已知椭圆C和C的中心为坐标原点O，两椭圆的长轴为MN（在x轴上），短轴长分别为2m，2n（m>n），直线l（过原点且不与x轴重合）与C，C的四个交点为A，B，C，D. 若λ=，△BDM和△ABN的面积分别为S和S.

（1）当直线l与y轴重合时，若S=λS，求λ的值;

（2）若λ变化时，是否存在这样的直线l，不与坐标轴重合，且使得S=λS？

题目解析：根据题意，设椭圆C的方程为+=1，椭圆C的方程为+=1，其中a>m>n>0，λ=>1.

（1）如图3所示，当直线l与y轴重合时，则S=BD·OM=a·BD，S=AB·ON=a·AB，所以=. 令x=0，将其代入C和C的方程中，得y=m，y=n，y=-m，于是===. 因为S=λS，所以=λ，化简得λ2-2λ-1=0. 因为λ>1，解得λ=+1. 所以，当直线l与y轴重合时，若S=λS，则λ=+1.

（2）若存在这样的直线l，不妨设直线l的方程为y=kx（k>0）. 设点M（-a，0），N（a，0）到直线l的距离分别为d，d，则d=d. 所以S=BD·d，S=AB·d，所以====λ，所以=.

由点A（x，kx），B（x，kx）分别在C，C上，可得+=1，+=1，两式相减得+=0，解得k2=. 因为k2>0，且x>x，所以λ2x-x>0，所以1<<λ.

反思：本题看似简单，但是充分考查了学生运算求解的能力，数形结合思想的应用更能考核学生的数学应用能力.

总之，在日常的教学中要重视培养学生提取信息的能力和迁移信息的能力，让学生通过对信息的加工和重组找到解决问题的方法，从而逐渐培养学生的应用意识和创新意识.

3242500589214