逆向思维在小学数学教学中的应用探讨
龚成兵
[摘 要] 逆向思维作为一种独具特色的思维模式,在发展学生数学学习能力的同时能达到优化学生思维品质的作用。尝试探讨逆向思维在“图形与几何”“数与代数”“实践与综合应用”等板块中的应用,以发展学生空间观念、数感与运算能力、解决问题能力。
[关键词] 逆向思维;小学数学;应用
逆向思维又被称为“反过来思考”,其作为一种独具特色的思维模式,在数学学习中发挥了重要作用,指引学生从事物的结尾向事物发展的反向思考,在思考过程中抽象出事物发展规律,由此大大提升学生解决问题的能力,在发展学生数学学习能力的同时达到优化学生思维品质的作用。基于此,笔者尝试探讨逆向思维在小学数学教学中的应用,期望能够起到抛砖引玉的效果。
一、在“图形与几何”中巧用逆向思维,发展学生的空间观念
“图形与几何”板块是小学数学知识体系的重要组成部分,其主要包括图形的认识、图形的测量、图形的运动和图形与位置四个部分。空间观念是一个综合能力,它包括了观察能力、想象能力、抽象能力等数学能力。在教学中,教师往往关注把几何图形与现实生活联系起来,把几何图形与数学操作结合起来,却对逆向思维在“几何与图形”板块的运用缺乏足够的关注度。那么,如何在“几何与图形”教学中,巧用逆向思维发展学生的空间观念呢?
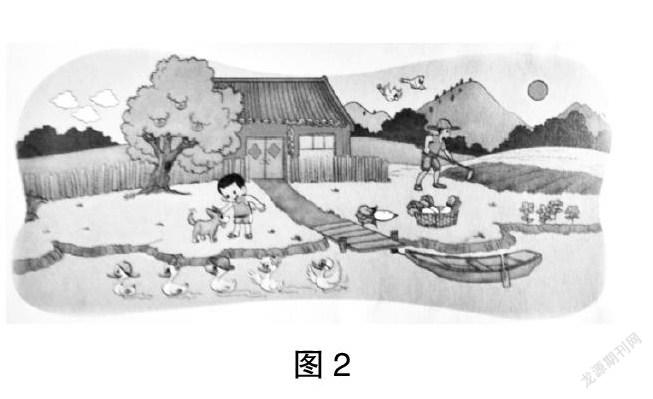
师:有两个正方形,A点是大正方形的中点,小正方形的边长是2厘米,大正方形的边长是4厘米,求图中(见图1)①和②两个图形的面积之和。
生1:所求图形是由两个三角形组成的。
生2:求三角形的面积需要知道三角形的底和高,但是现在既不知道三角形的底,又不知道三角形的高。
(学生的思维陷入停滞。)
师:既然顺着思考行不通,我们是不是可以转变思路进行逆向思考呢?
(学生讨论。)
生3:我知道了。既然不能直接求出图中①和②两个图形的面积,那么我们可以尝试求出除了①和②两个图形之外的图形的面积,这样也可以解决问题。
生4:对,除了①和②两个图形之外的图形是由两个规则的图形组成的,其中一个是三角形,另一个是梯形。
师:那么,你能试着求出三角形和梯形的面积吗?
生5:三角形的面积=底×高÷2=2×4÷2=4(cm2),梯形的面积=(上底+下底)×高÷2=(2+4)×4÷2=12(cm2),然后再求出两个正方形的面积之和是(2×2)+(4×4)=4+16=20(cm2),所以①和②两个图形的面积之和是20-12=8(cm2)。
要顺利解决这一问题,学生至少需要具备两个方面的能力:一是要具备一定的观察能力和空间想象能力,学生要能够敏锐地看出各个图形之间构成的关系,并把这种关系运用到问题解决之中。二是要具备逆向思维能力。如果本题采取“从正面突破”的策略,无疑将增加本题的难度,但只要学生巧妙地采取“迂回”的办法,通过分析两个未知大小的图形与两个规则图形的关系,先求出两个规则图形的面积,然后再反向算出未知大小的图形的面积,使得问题的解决变得更具灵活性和巧妙性。由此可见,本题从观察能力、空间想象能力和逆向思维能力三个角度提升了学生的数学学习能力、优化了学生的思维品质、发展了学生的空间观念。
二、在“数与代数”中巧用逆向思维,发展学生的数感和运算能力
“数与代数”板块的内容大体上可以分为数的认识、数的运算、式与方程等内容。“数与代数”板块的重要教学目标就是培养学生的数感,提升学生的运算能力。
1. 运用逆向思维,发展学生的数感
数感是新课标提出的核心概念之一。新课标指出:“在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。”所谓数感,就是对数的理解和感悟。具体来说,数感可以分为以下几个方面:能够用多种方法表示数;能在具体情境中把握数的相对大小;能用数来表达和交流信息;能为解决问题选择适当的算法等。数感并非为了数学学习而定义出来的数学概念,其本身就贯穿于数学教学的全过程中。在教学中,教师应注重发挥逆向思维在培养学生数感方面的作用,这能起到事半功倍的效果。
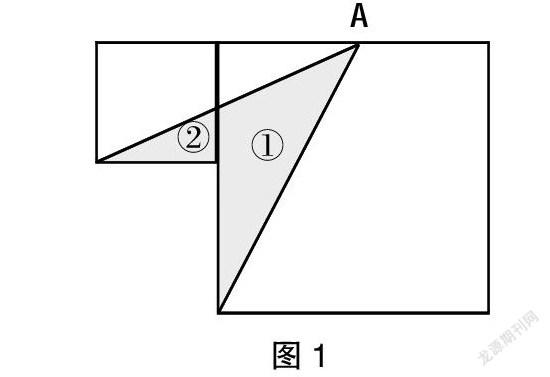
比如在讲解“认识1~5”时,教师为学生出示了一幅图(如图2所示)。教师先引导学生认识1个太阳、1棵苹果树,2只小鸟、2个人,3朵白云、3个苹果、4朵花、5只小鸭子,从而引导学生在清晰实物的基础上抽象出数学符号,认识1、2、3、4、5。在此基础上,教师再引导学生反向思考:“1”除了可以表示1个太阳、1棵苹果树外,还可以表示什么?学生纷纷回答:“1”还可以表示1条小船、1支铅笔、1个汉堡,凡是数量是1的物体都可以用“1”来表示。“2”除了可以表示2只小鸟、2个人以外,还可以表示什么?学生回答:“2”还可以表示2只鱼、2瓶水,凡是数量是2的物体都可以用“2”来表示……
教学中,教师引导学生经历从实物到符号的正向思考,又使学生体验从符号到实物的逆向思考,从多个角度使学生真正理解数学符号的内涵,这种正向思考和逆向思考相结合的教学方式能提升学生的思维灵性、优化学生的思维品质、发展学生的数感。
2. 运用逆向思维,提升运算能力
新课标指出:“运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。”运算能力是小学生数学核心素养的重要组成部分,运算教学贯穿于小学数学教学的始终。在运算教学中,加法与减法、乘法与除法互为逆运算,教师在四则混合运算的讲解过程中,可使学生逆向思考,经历逆向运算的过程往往能够促进学生对算理的理解,还能够节省运算时间,提升运算的准确度。
比如在讲解“乘除法”时,教师设计了这样的题目:“桌子上有5个盘子,每个盘子里有3个苹果,一共有多少个苹果?”学生列式为3×5=15(个)。接着教师变换题目:“一共有15个苹果,每个盘子里放3个苹果,一共需要几个盘子?”学生思考后列式15÷3=5(个)。在讲解“混合运算”时,教师设计了这样的题目:9+99+999+9999+99999。如果按部就班地从左到右的顺序逐一相加非常麻烦,教师可引导学生逆向思考:运用减法运算是不是会简便一些?在教师的启发下,有学生列出了这样的式子:(10-1)+(100-1)+(1000-1)+(10000-1)+(100000-1)=111110-5=111105,这就使得计算过程大大简化了。又如在讲解“乘法分配律”时,学生对于(a+b)×c=a×c+b×c熟记于心,却对a×c+b×c=(a+b)×c不甚熟悉。為此,教师设计了这样一道题:3.7×76.8+23.2×3。教师引导学生先把3转化为3.7,然后再通过乘法分配律的逆运算a×c+b×c=(a+b)×c,实现运算的简便化。
乘法与除法、加法与减法、乘法分配律的互逆运算,学生经过了正向和反向的双向思考,丰富了学生对运算本质的理解,锻炼了学生的逆向思维能力,提升了学生的运算能力。
三、在“实践与综合应用”中巧用逆向思维,发展学生解决问题的能力
“纸上得来终觉浅,绝知此事要躬行”。提升学生的思维能力不能“纸上谈兵”,必须使学生在解决问题的过程中不断提升能力、发展素养。小学数学中的“实践与综合应用”板块致力于引导学生通过学到的知识解决实际问题。在这个过程中,当学生的正向思考遇阻时,教师要引导学生从反向进行思考,或许学生就会有不一样的思维体验。
比如教师出示了这样一道题目:淘气有一些课外书,他送给笑笑5本,妈妈又给淘气买了9本,这时淘气一共有课外书20本,那么淘气原来有多少本课外书?由于低年级学生尚未接触到方程的知识,因此本题对于他们而言有一定的困难。教师启发学生转变思考路径,学生通过反向思考,列出算式20-9+5=16(本),问题由此得以顺利解决。
解题中,当学生的思维受阻,甚至陷入停滞时,教师可引导学生进行逆向思考,从而为学生的思维打开“另一扇窗”。在学生进行逆向思考的过程中,不但让数学问题迎刃而解,而且学生的知识得到了拓展,解决问题的能力得到了提高。
总之,在小学数学教学中,教师要深入挖掘教材中训练学生逆向思维的生动素材,并将这些“反其道而行之”的内容恰到好处地呈现给学生,指导学生逆向思考,以果索因、正逆互换,发展学生的空间观念、数感和运算能力,提升解决问题的能力。

