地方政府或有隐性债务风险预警系统构建与应用研究——基于BP神经网络分析法

李丽珍

(中国社会科学院工业经济研究所，北京 100006)

一、引 言

风险是不愿意发生的事件发生的不确定性[1]，是事后才掌握的不确定性因素所造成的损失[2]。风险包括三个基本要素：有害的结果、发生的概率和现实状态[3]。关于政府债务风险，有学者强调政府债务持续增长将引发债务违约风险或货币贬值风险[4]，有学者认为政府债务占GDP比例达到一定程度将使政府面临财政可持续性风险，还有学者认为政府债务超常增长、过快增长将引起规模失控风险、结构失衡风险、管理无效风险及外在冲击敏感性风险等。债务风险界定问题看似简单，实则复杂且极为关键，将关系到风险评估、预警和防范机制设置。本文认为政府债务风险是政府债务不断增长过程中对经济社会产生不良影响的不确定性、不可测性及其造成的损失或后果。

随着我国经济增速下滑，政府、企业和个人杠杆率居高不下，各种不确定性因素叠加，以及金融工具创新下债务形式更为多样化、隐蔽化，地方政府债务风险呈上升趋势，尤其是政府担保类、救助责任类隐性债务风险。十九大报告提出要坚决打好“防范化解重大风险攻坚战”，2019年12月中央经济工作会议强调要以“六稳”来应对内外挑战，缓解经济下行压力，缓释各类风险。稳预期、稳金融、稳投资需以稳杠杆为前提。政府隐性债务是指非由法律或合同规定的，而是由中长期公共支出政策中预先确定的责任所形成的债务，以及依赖于特定事件发生才形成的、政府迫于公众预期、道义责任或政治压力而承担的债务。地方政府隐性债务风险或将成为地方财政最主要的风险来源。如何防范和化解地方政府隐性债务风险以确保地方财政可持续性，避免发生系统性金融风险，已成为学界和业界关注的焦点。

从政府债务风险防控角度，Brixi(2012)指出政府债务风险控制的最佳时机是在债务风险爆发之前，借助政府会计对债务信息进行及时记录、识别和披露[5]。刘尚希等(2017)认为公共债务的治本之道在于有效识别和预警风险，进而依托政府和市场的力量协同治理[6]。魏加宁等(2010)认为政府债务的公开化与透明化是化解地方债务问题的前提，应从完善政府会计制度和构建地方政府债务报告制度着手[7]。刘尚希(2005)指出应通过降低公共债务的不确定性程度来改善政府财政风险状况[8]。Yu(2016)认为PPP项目政府担保是政府资产负债表中隐性债务的构成要素之一，很可能被过度使用从而恶化财政负债[9]。杨志勇等(2017)从国家资产负债表角度提出地方政府债务风险并非只与债务本身、财政收入等普遍关注的变量有关，还与政府所拥有的资产——土地出让金、国有经济、矿产资源等密切相关，应通过构建资产与负债的对应关系来全面分析政府债务风险[10]。赵全厚(2014)认为应将地方政府及其附属机构视为类似于企业的经济人，将地方政府性债务划分显性债务和隐性债务，并以科学方法评估各自风险[11]。邢俊英(2004；2006)认为直接隐性负债若在发生之前不予反映，将会造成当期财政支出低估，加大财政负债风险隐患，政府会计改革重在对直接隐性负债和或有负债的确认、计量和报告作出科学合理的规定[12]；收付实现制的会计制度掩盖了政府资源和支出责任的全貌，无法真实反映政府资产负债信息，使得大量负债被隐匿，容易错失风险防控的最佳时机[13]。上述研究均突出强调了政府债务信息披露的必要性以及提前预警的重要性，但值得注意的是，无论是《中华人民共和国预算法》还是我国的政府财务报告制度，均没有对政府或有隐性债务的披露提出要求。

风险预警是根据风险综合评价结果发出风险等级警示信号，为提早应对和处置提供决策指导。债务风险预警的基础是债务风险评估，而债务风险评估是一个复杂体系，涉及多项指标、多个主体，各项指标与各个主体之间还具有风险相互传染性，各指标对债务风险产生影响的结构关系应是非线性的。因而只有构建包含多项输入指标、多层交叉传递关系的非线性仿真模型，才能形成科学、客观、切合实际的地方政府债务风险预警效果。预警系统的设计要反映多指标输入和输出的复杂网络过程，输入指标和输出结果之间存在非线性映射关系。这就使得传统显性的、线性化的函数如Logistic模型、KNN模型、多元判别分析模型等在刻画债务风险方面的精度和稳健性效果往往受到质疑。为此，我们需要适用于多层网络学习的、可对多层权系数进行反复修正的反向传播学习算法，即BP神经网络法。BP神经网络对复杂的非线性关系具有较强的拟合能力，且学习规则简单，自我学习能力强，稳健性优良，目前已在自动控制、函数逼近、仿真、预测等领域中得到广泛应用。国内越来越多学者运用BP神经网络法构建地方政府债务风险预警系统，较具代表性的做法有洪源和刘兴琳(2012)采用粗糙集-BP神经网络方法构建并实证检验了地方政府债务风险非线性仿真预警系统[14]，马恩涛和吕函枰(2017)采用灰色关联度与BP神经网络相结合方法构建并实证检验了重庆市地方政府债务风险预警系统[15]，刘骅与卢亚娟(2014)运用因子分析-K均值聚类算法与BP神经网络法构建平台债务“风险阈”预警模型[16]，洪源等(2018)采用TOPSIS-AHP法和K均值聚类法结合GA-BP神经网络算法构建地方政府债务风险非线性先导预警系统[17]，李斌等(2016)采用TOPSIS法、德尔菲法结合BP神经网络法和支持向量机法构建基于结构风险最小化的地方政府债务风险预警模型[18]。

从已有研究可知，BP神经网络分析法一般辅以粗糙集、灰色关联度等指标约简方法，在债务风险评估方面主要采用K均值聚类算法、信息熵、AHP法、TOPSIS、德尔菲法等。方法众多，各有优劣，方法的选择主要基于样本数据规模、特征进行综合权衡等。不过，已有研究中尚缺乏对地方政府或有隐性债务的评估及预警，也鲜有对省级数据进行的实证研究。本文综合应用AHP、熵值法与BP神经网络法，构建包含显性债务风险、或有隐性债务风险和财政经济运行风险在内的地方政府或有隐性债务风险预警指标体系，充分利用BP神经网络的多层网络、反向传播学习优势来刻画复杂的、非线性的或有隐性债务风险结构，可提高风险预警效率和客观性，为政府提早应对风险、安排偿债优先秩序、优化财政收支结构等提供信号导向和政策参考。

二、地方政府或有隐性债务风险非线性仿真预警系统构建

(一)BP神经网络算法的基本原理

BP神经网络法是通过模拟人脑神经处理信息、作出决策的过程，构建由多个基本神经元相互连接的网络系统，对各类信息进行反复输入、处理、输出的方法，其网络层次包含一个输入层、若干个隐含层(≥1)和一个输出层(如图1所示)。

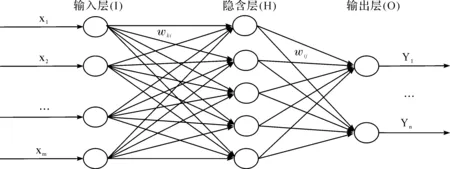
图1 BP神经网络结构示意图

其基本原理为：给定输入输出序列(X,Y)，输入层(I)节点数目m，输出层(O)节点数目n。在输入层和输出层之间有若干个隐含层(H)。假定隐含层个数为h，输入层和隐含层之间的权值wki和阈值调整ai，隐含层和输出层之间的权值wij和阈值bj。给定学习速率和神经元激励函数，隐含层输出公式为：

其中，f为隐含层函数，设定其形式为非线性可微非递减Sigmoid函数f(x)=1/(1-e-x)，其变化范围为(0，1)，导数形式为f′(x)=f(x)[1-f(x)]。同时，输出层公式为：

计算均方根误差E公式。BP神经网络具有信息输入正向传播，误差在学习过程中反向传播修正特征，在反复训练和学习中达到输出值Oj与期望值Yk之间的渐进拟合，误差项越来越小直至达到预设阈值而停止学习，误差函数E(w,b)为：

从公式推导过程可知，当隐含层节点数足够多情况下，在隐含层中使用非线性可微非递减的Sigmoid函数，在输出层中使用线性传输函数，即可较好地逼近对象函数，表明BP神经网络作为一种多层前馈网络，具有较强非线性映射能力和泛化能力。

(二)基于BP神经网络的地方政府或有隐性债务风险预警指标体系设计

裴育和欧阳华生(2007)认为全方位的债务风险预警系统应以债务风险矩阵中四类负债项的风险为框架，并建议：限于数据可得性，可从显性债务风险开始进行循序渐进式建模；直接隐性债务列入预算或中长期预算以便准确计量；对隐性债务进行显性化预算管理；对或有隐性债务开展财政损失估计和发生概率估计等[19]。本文依照科学性、系统性、相关性、数据可得性原则，将形成地方政府性债务风险的内部和外部影响因素分解为显性债务风险、或有隐性债务风险和宏观经济财政运行风险，三类风险因素相互影响、相互作用。细化三类风险影响因素的具体衡量指标作为风险预警指标，从而形成包含11项二级预警指标的地方政府或有隐性债务风险预警指标体系。其中各二级指标根据风险大小划分为“轻警”“中警”和“高警”三个区间。结合我国地方政府债务特征，设定各项指标的预警区间分布(见表1)。

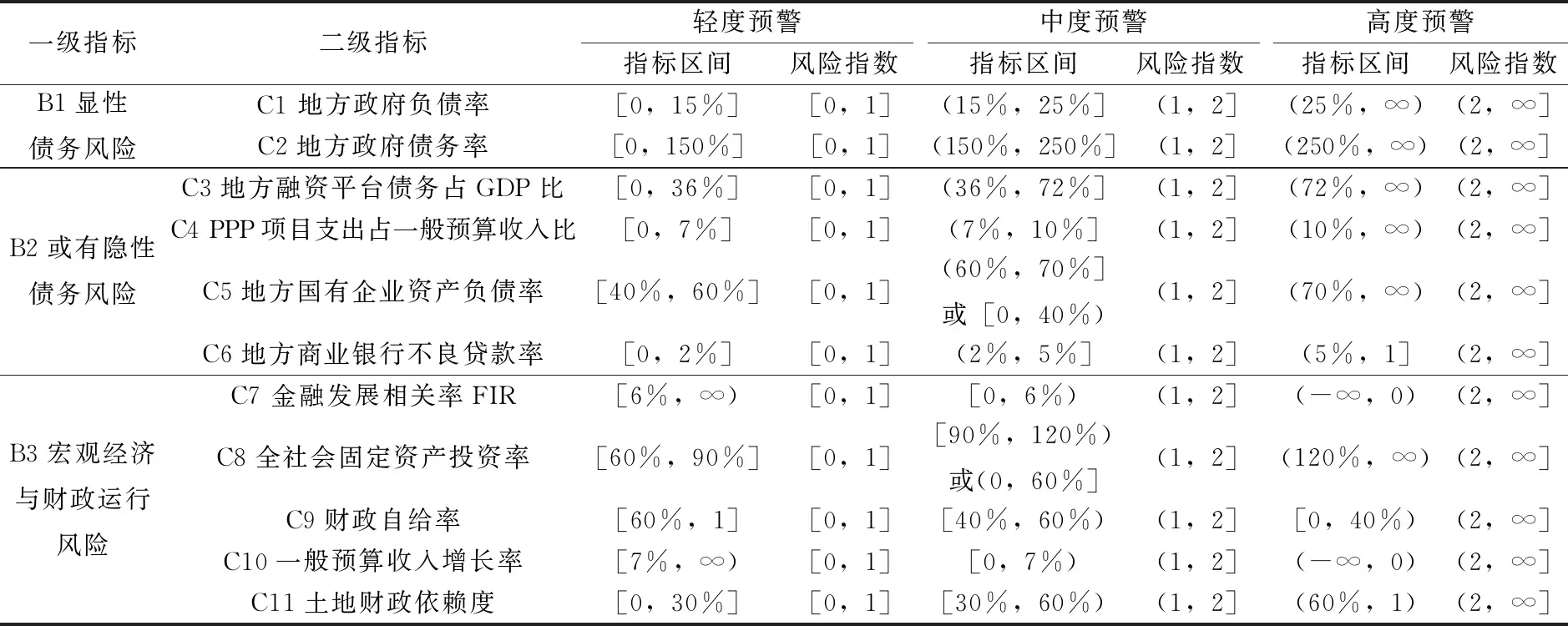
表1 地方政府或有隐性债务风险预警指标体系构建

各项指标预警区间根据通用惯例、均值、经济目标等方面综合考量设置。其中，地方政府债务率根据国际通行警戒标准设置150%以下为轻警区域，250%以上为高警区域。或有隐性债务的指标选取及预警区间设置依据如下：

(1)C3地方融资平台债务占GDP比例。地方融资平台债务发起设立者是地方政府，开展投融资活动的主导者是地方政府，形成庞大债务也主要依托于地方政府信用担保，属地方政府的或有隐性债务。本文以其债务占GDP比例衡量来自融资平台的债务风险，反映地方经济对融资平台债务的承载情况。2017年该指标的全国均值为36%，设置36%以下为安全区域，72%以上为高警区域。

(2)C4 PPP项目支出占一般预算收入比例。将PPP项目纳入或有隐性债务考核体系主要基于如下考虑(李丽珍，2020)[20]：政府付费型和缺口补助型PPP项目中的债务融资部分属地方政府直接隐性债务；PPP项目运作失败风险、延期支付风险、信用违约风险可能形成政府救助责任债务；“明股实债”属违法违规类隐性债务。限于数据可得性，本文仅以PPP项目年度财政支出占一般公共预算支出比例作为PPP项目类政府或有隐性债务风险指标。预警区间设置如下：对2015～2045年间财政支出占比在7%～10%的作为中警区，7%以下为安全区域(1)根据《财政部关于印发<政府和社会资本合作项目财政承受能力论证指引>的通知》(财金〔2015〕21号)第二十五条规定：“每一年度全部PPP项目需要从预算中安排的支出责任，占一般公共预算支出比例应当不超过10%”。财政部金融司2018年5月发布的《筑牢PPP项目财政承受能力10%限额的“红线”——PPP项目财政承受能力汇总分析报告》列出2015～2045年各省市支出责任总额，并将支出占比7%以下视为安全区域。，10%以上为高警区域。

(3)C5地方国有企业资产负债率。当地方国有企业出现债务偿付危机，政府按照契约精神需按依据出资比例承担必要清偿责任，出于维稳和道义责任角度还可能会承担更高比例救助，因此地方国有企业债务是地方政府的或有隐性债务。从财务稳健性角度，一般企业资产负债率大于70%时表明风险较大，适宜水平为40%～60%。因此，本文分别以40%和70%作为此项三类警戒区的分界点。

(4)C6地方商业银行不良贷款率。当商业银行陷入流动性不足、资本充足率过低、不良贷款率过高等困境时，地方政府迫于社会公众压力和防范公共风险需要往往需实施救助，这就形成政府负有救助责任的债务。根据2006年银监会发布的《商业银行风险监管核心指标(试行)》要求，商业银行不良贷款率不应高于5%，本文设定5%为高度预警，而根据近年该指标基本维持在2%水平以内，总体处于安全状态，因此将0～2%划定为轻度预警区。

三、地方政府或有隐性债务风险非线性仿真预警系统应用

(一)样本数据来源与离散化处理

以2017年我国31个省区市各项政府债务指标为样本，对样本数据进行离散化处理，以每项指标的样本数据与表1预警指标区间进行对照后赋值：落在“轻警”区间，则赋值为1；落在“中警”区间，则赋值为2；落在“高警”区间，则赋值为3。数据来源方面，地方政府显性债务数据2010～2015年来源于万德数据库，2016～2017年来源于财政部官网公告；地方国有企业债务、资产负债率、财政收支数据来源于历年《中国财政年鉴》；商业银行不良贷款数据来源于银监会官网发布的各年度《中国银行业监督管理委员会年报》；地方融资平台债务数据来源于万德数据库和各级财政决算报告；国有土地使用权出让金收入数据来源于《中国国土资源统计年鉴》，其中2017年数据根据2014～2016年各省区市平均值对2017年度全国国有土地使用权出让金收入总额进行比例分摊得到；未做特别说明的其他数据均来源于中经网与万德数据库。处理结果如表2所示。

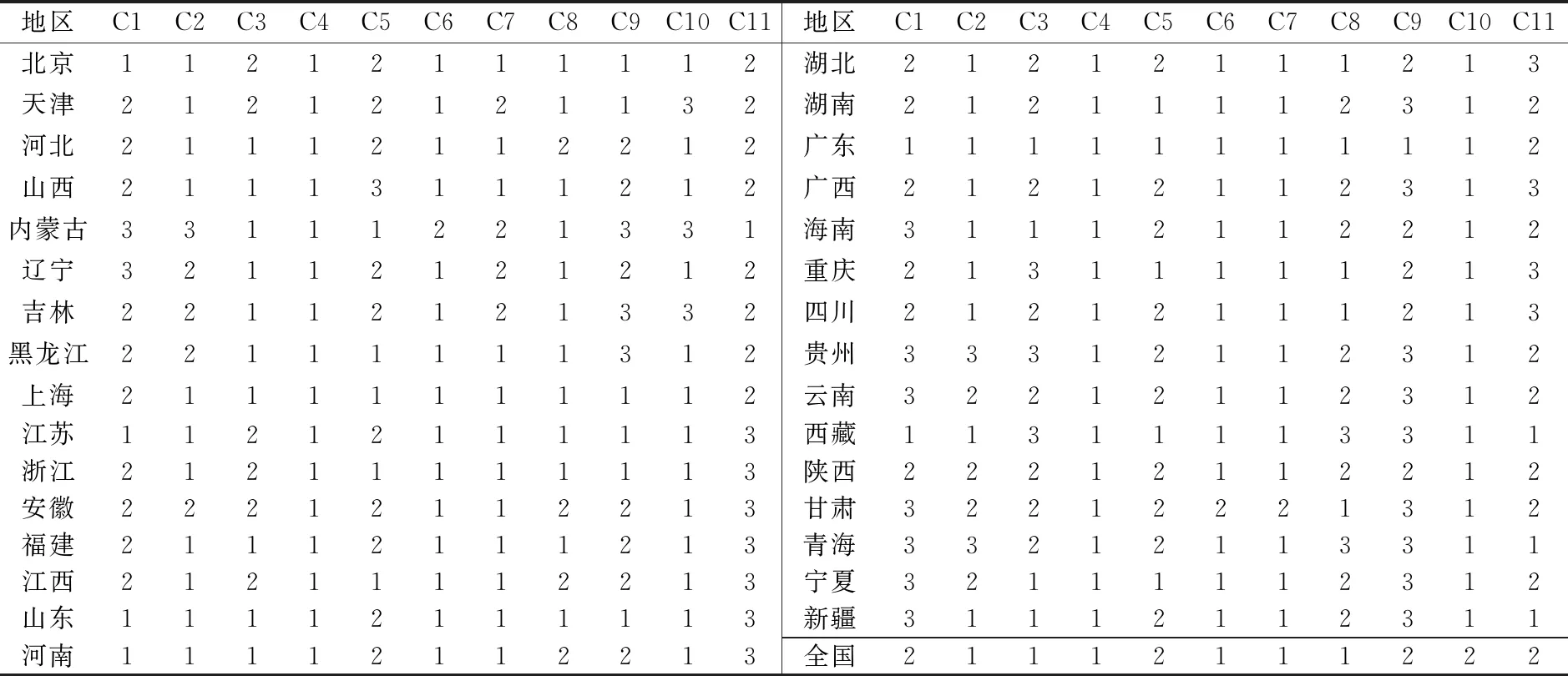
表2 各地区地方政府或有隐性债务指标离散化预警指标属性决策值

(二)地方政府债务性风险的综合评价

采用层次分析法(AHP法)和熵值法对地方政府或有隐性债务风险预警指标体系的各项指标进行主观、客观综合赋权，进而对地方政府债务风险进行综合评价。

1.基于AHP法的主观赋权

将地方政府或有隐性债务风险预警指标的目标指标、一级指标、二级指标分别设定为目标层、准则层、方案层，进而构造成对比较阵，邀请5位专家对分层指标进行两两比较式评分、决策，经过AHP法处理后，各指标权重如表3所示。

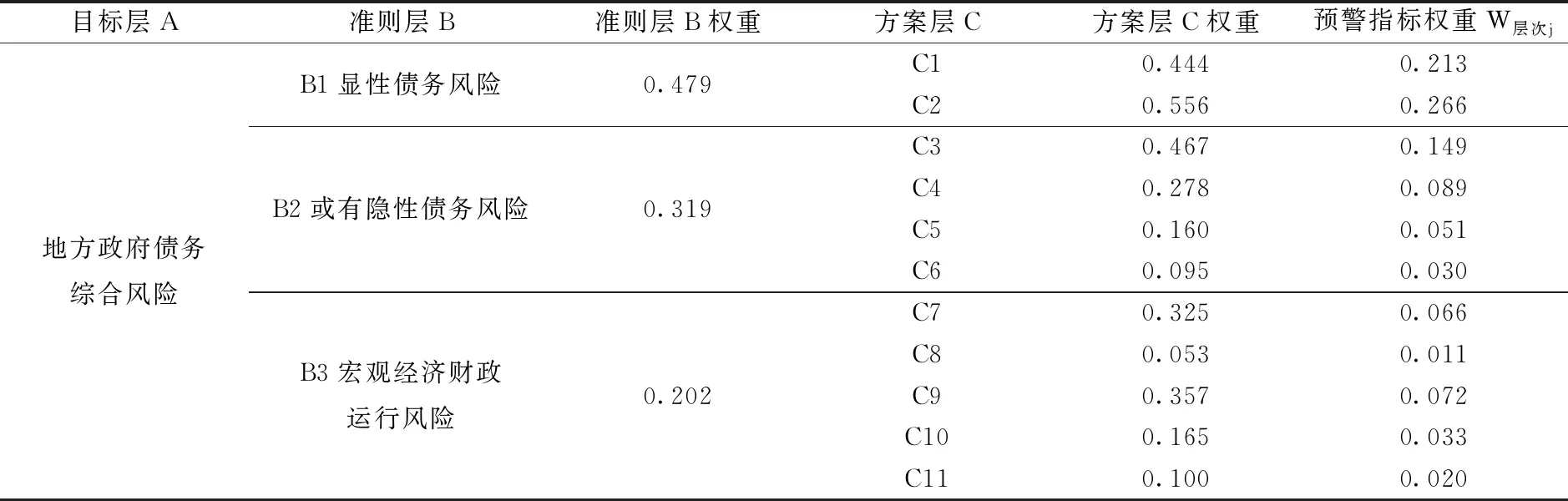
表3 基于AHP法的预警指标主观权重

进一步对判断矩阵进行一致性检验，结果如表4所示，方案层C对于准则层B、准则层B对目标层A的一致性比例均小于0.01，表明判断矩阵通过一致性检验，权重分配合理。

表4 AHP法的一致性检验结果

2.基于熵值法的客观赋权

采用熵值法，根据各项指标离散程度来确定指标权重，离散程度越大，表明该指标对综合评价的影响越大，权重就越高。首先，将31个省区市11项评价指标的原始数据矩阵表示为：

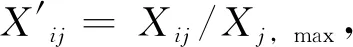
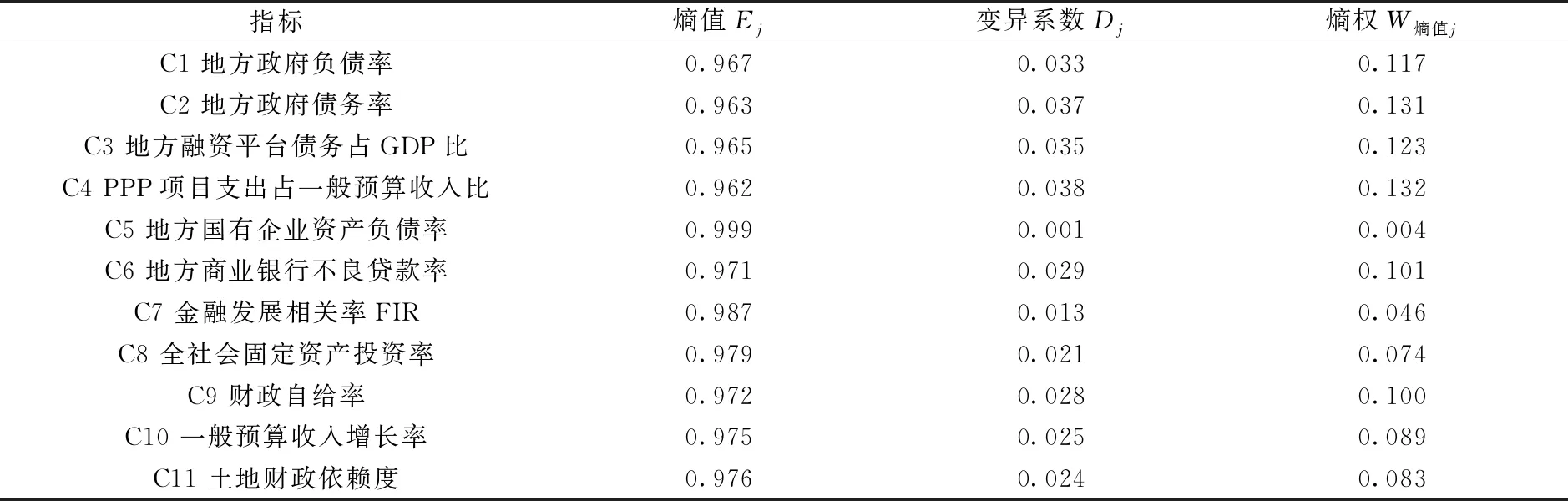
表5 基于熵值法的各项预警指标客观权重

3.主客观结合的地方政府或有隐性债务综合权重

根据表3和表5主客观权重计算综合权重，即W综合j=θW层次j+(1-θ)W熵值j，其中θ为AHP法赋权的权重系数，本文认为主客观赋权法各有优劣，同等重要，因而将θ设置为0.5，综合权重如表6所示。从表6可知，地方政府或有隐性债务风险预警指标中，C1地方政府负债率、C2地方政府债务率、C3地方融资平台债务占GDP比、C4 PPP项目支出占一般预算收入比以及C9财政自给率的权重均大于8%，是关键性指标，应给予高度关注，建立动态监测机制。

表6 基于主客观赋权的预警指标综合权重

4.全样本下政府或有隐性债务风险综合评价结果

根据预警指标综合权重，计算2017年各省区市政府或有隐性债务风险综合评价值Vi：

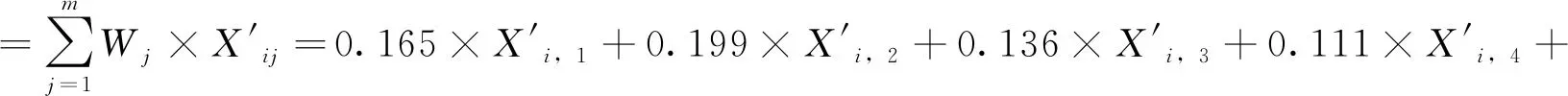
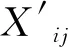
如表7所示，地方政府或有隐性债务风险处于轻警状态的省区市有10个，占比32%；处于中警状态的有20个，占比64.5%；处于高警状态的有1个，占比3.2%。可见，过半地区处于风险中警以上，风险普遍较高。其中西部12个省区市中，贵州处于高警状态，其余11个省区市处于中警状态；中部8个省除了山西、河南和湖北为轻警状态外，其余全部处于中警状态；东部11个省市中，天津、辽宁、江苏和海南处于中警状态，其余省市均处于轻警状态。风险主要集聚于西部地区，有如下原因：西部地区本身经济基础薄弱，债务占比相对较高；财政自给率普遍偏低，对举债需求更为强烈，融资平台债务占比普遍较高；“补短板”供给侧改革背景下大量PPP项目集中于贵州、新疆等西部地区，加大了或有债务风险。

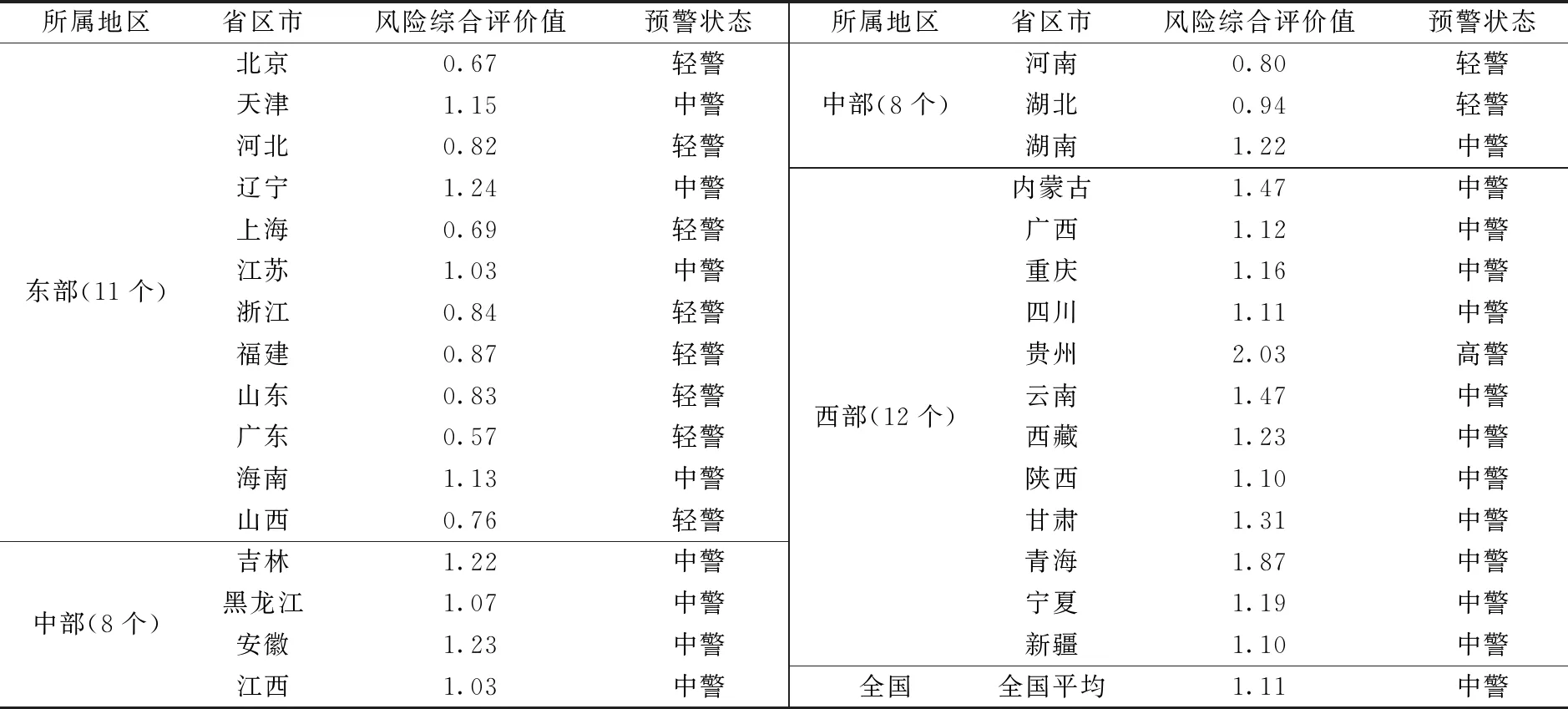
表7 2017年各地区地方政府或有隐性债务风险综合评价结果

(三)非线性仿真预警系统的训练与检验

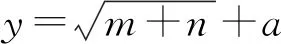
(1)对原始输入数据进行归一化处理。训练样本数据采用Premnmx函数归一化为[-1,1]，检验样本数据采用Tramnmx函数归一化为[-1,1]；

(2)根据构建的网络结构特点，采用Trangsig函数作为传递函数中输入层至隐含层的函数、采用Purelin函数作为传递函数中隐含层至输出层的函数，采用基于贝叶斯正则化算法的Trainbr函数作为训练函数；

(3)设定目标误差为0.001、最大训练迭代次数为1000次、学习率为0.01；

(4)采用26个样本对神经网络进行训练。

如图2所示，BP神经网络训练误差变化曲线有四条线构成。训练线描述BP训练过程的均方误差(Mean Squared Error, MSE)指标表现；测试线描述BP测试过程的MSE指标表现；理想线表示BP网络训练到第10次时BP训练结果最理想；目标线是ANN工具箱训练BP时设置的网络训练停止目标。其中，理想线与目标线重合。当网络训练迭代至第10次时，网络输出误差达到设定的训练精度，网络收敛于最优稳态值。训练得出的期望输出与实际输出拟合度较高，二者MSE指标仅为0.00096，训练效果好，预警准确性高。

(5)随机检验。将随机抽取的5个测试样本放入训练好的BP神经网络中，得到的预警结果如图3所示。测试样本仿真值(圆点)和真实值(星号)较为接近，二者拟合度为97.9%，二者均方误差仅为0.00749，说明仿真效果良好，预警效果较为理想。

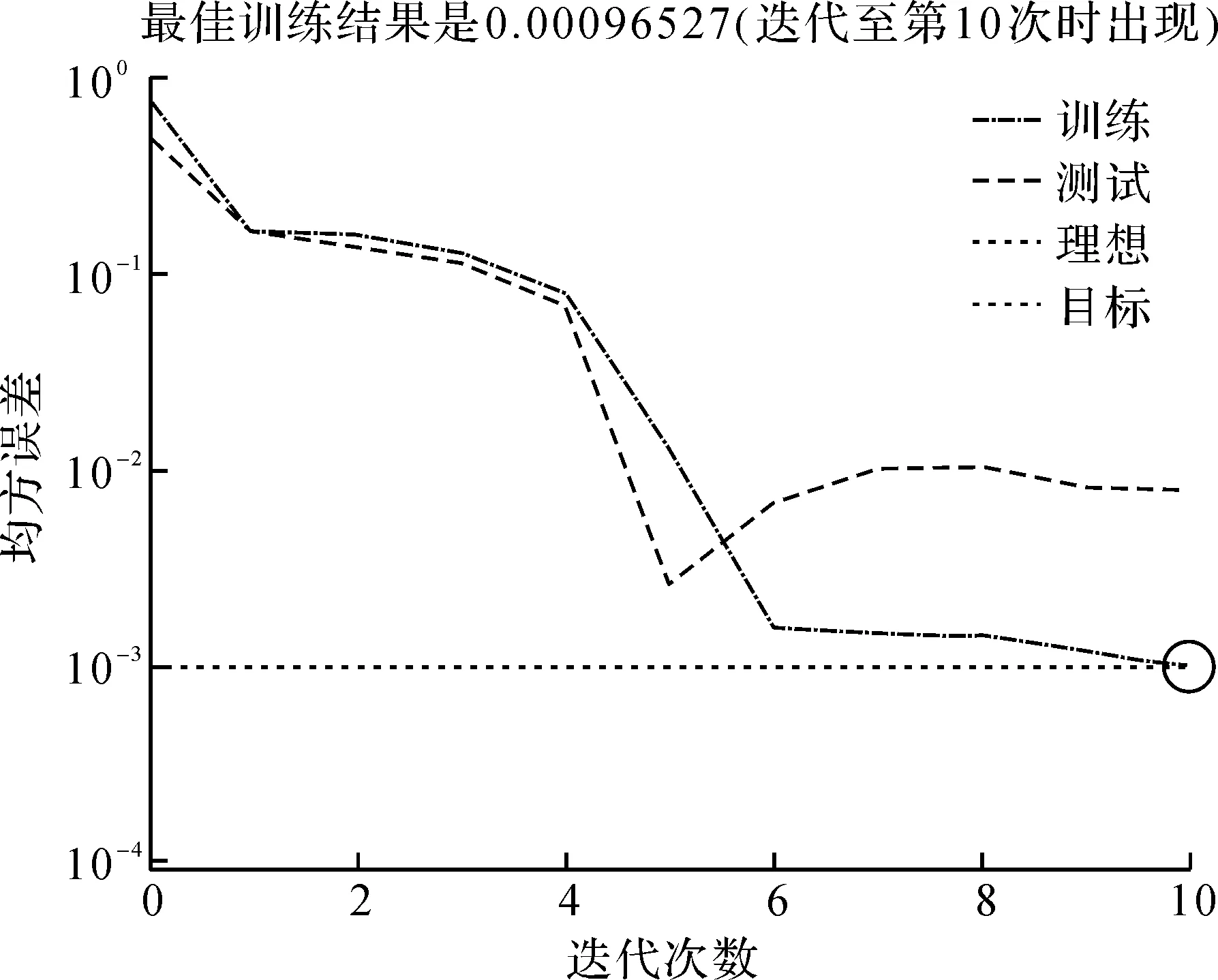
图2 BP神经网络测试样本仿真值与真实值曲线图

图3 BP神经网络训练误差变化曲线

检测样本的仿真结果(见表8)表明，5个样本的仿真效果均在90%以上，所构建的BP神经网络非线性仿真预警系统较为可靠，可作为地方政府或有隐性债务风险的预警体系。在此预警系统下，只要获取各省区市的债务指标原始数据，输入系统即可得出地方政府债务风险的“轻警”“中警”和“高警”状态，以及各类债务的风险聚集点，从而为财政提早应对、安排偿债优先次序、优化财政支出结构等提供参考，以有效防范地方财政风险。

表8 BP神经网络测试样本的仿真值与真实值对比

四、基于风险预警的地方政府或有隐性债务风险防控策略

构建地方政府或有隐性债务的风险预警系统对于提早防范风险有重要意义，但技术上构建预警系统之后，实践中地方政府在预警前期数据来源准备、预警结果分析、风险应对策略选择等方面还需进一步厘清。因此，基于所构建的预警系统，进一步设计地方政府债务风险防控基本流程及风险应对策略，对于提升预警决策和风险响应的速度和效率，有效防范和化解地方政府或有隐性债务风险亦十分重要。

(一)地方政府或有隐性债务风险防控基本流程设计

地方政府或有隐性债务风险防控基本流程依照风险管理理论的内涵及基本程序进行设计，具体为“原始数据收集—数据预处理—风险监测—风险识别—风险度量—预警报告—预警决策—风险应对—动态监测”，各环节依次、逐级完成，形成快速报告和响应机制(见图4)。其中，风险度量和预警决策环节是核心。风险度量建立在可量化的风险评价指标体系基础之上。基于已构建的风险预警系统，原始数据采集包括显性债务数据、隐性债务数据以及宏观财政、金融及其他经济数据。地方政府根据预警的“轻警”“中警”“高警”结果，选择恰当的风险防控策略。

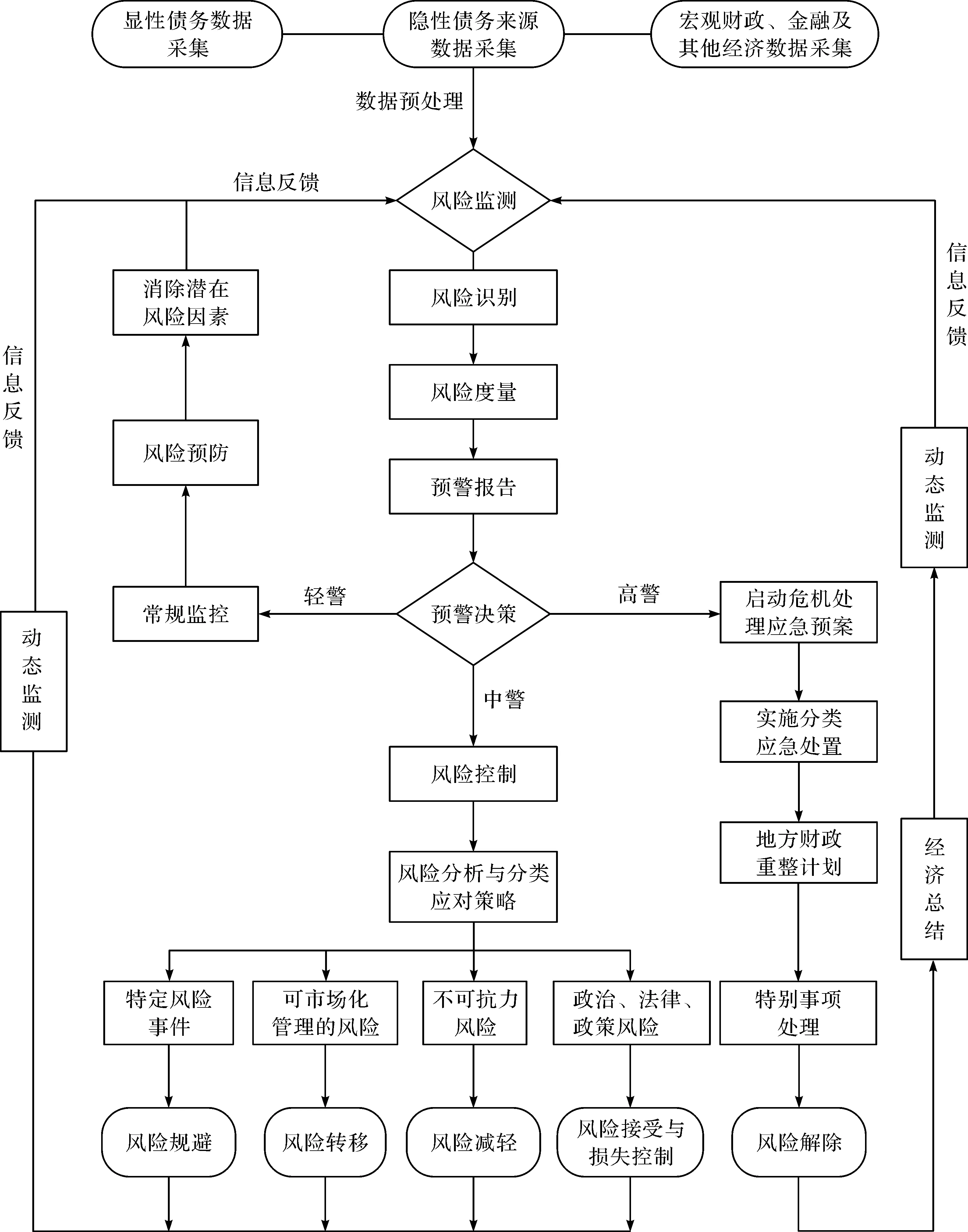
图4 地方政府或有隐性债务风险防控基本流程

(二)预警决策与风险防控策略

在预警决策和风险应对方面，“轻警”只需常规监控，做好风险预防，消除潜在风险因素即可。“高警”则需引起高度重视，启动应急处置预案，成立由“一把手”牵头的危机管理领导小组推进实施应急处置，直至风险解除。“中警”情况发生概率相较于“高警”更大，是风险防控的重点，需引起足够重视，首先进行风险控制以避免态势进一步恶化，其次根据风险类别、特征进行分类处置、动态监测和信息反馈。具体分类应对策略如下：(1)风险规避。对于特定风险事件可能带来的危害，采用风险规避策略消除，如技术风险，采用更成熟的技术来规避；项目管理风险通过组建更成熟的运营团队来规避；以政府购买服务替代政府自主供给。(2)风险转移。将风险后果转移给第三方，如购买自然灾害保险、建立存款保险准备金制、推进养老基金中央调剂制度等都是转移地方政府救助责任负债的重要举措；又如将PPP项目建设进度风险，技术风险等通过签订合同约定社会资本方来承担。(3)风险减轻。将风险发生的可能性及其后果降低到一个可接受的范围。对于PPP项目中的定价风险、政治风险、法律和政策风险，政府可通过与社会资本方细化各类风险下的政府负担方式，或减轻法律变更所引发的政府补贴、税式支出激增的风险。(4)风险接受与损失控制。如不可抗力造成的风险以及政府承担兜底责任的风险，提早做好应急计划或预案，积极应对风险的各种后果。可通过地方政府税收、上级转移支付、对负债融资进行一定比例预扣、各类自愿性资产收入等组织偿债基金来源。根据债务风险预警等级不同，构建差异化、有针对性、相机抉择的政府偿债基金制度。

五、研究结论及政策建议

全国各省区市在经济实力与增速、政府财力与财政稳健性、债务规模与结构等方面均存在一定差异，尤其是政府隐性债务规模、结构及表现形式具有显著差异性，使得债务风险评估与防范变得尤为复杂。不能简单以债务规模占GDP比例作为衡量债务风险的唯一指标，而应构建多维、非线性的债务风险评估及预警机制。本文从系统论思想出发，依据形成地方政府隐性债务风险的内部和外部影响因素，综合应用AHP、熵值法与BP神经网络法，构建包含显性债务风险、或有隐性债务风险和财政经济运行风险在内的3项一级指标和11项二级指标的地方政府或有隐性债务风险预警指标体系。这与现有政府债务风险预警体系最大不同之处在于，在风险预警指标上，增加了或有隐性债务指标，并以“地方融资平台债务占GDP比例、PPP项目支出占一般预算收入、地方国有企业资产负债率、地方商业银行不良贷款率”等常规性、有可靠数据来源、代表地方政府隐性债务主要来源的比例性指标作为测度隐性债务风险评估的核心指标，有效避免采用绝对量指标可能存在的估计偏误；在研究对象上，以我国31个省区市为样本；在研究方法上，采用了更为客观、仿真效果更好的神经网络分析法。

通过地方政府或有隐性债务风险非线性仿真预警体系构建、模型应用及风险防控流程设计，得出如下结论及政策建议：(1)基于BP神经网络分析法构建的债务风险预警系统仿真效果良好，其政策意义在于可及时、客观反映地方政府债务风险的“轻警”“中警”和“高警”状态以及各类债务的风险聚集点，促进财政提早应对、安排偿债优先次序、优化财政支出结构、有效防范地方财政风险，同时有助于降低地方政府债务风险预警难度，提高预警效率及风险评估的客观性；(2)2017年全国有过半省区市或有隐性债务风险处于中警状态，且风险主要集聚于中西部地区，需加强对这些地区的融资平台债务、PPP债务融资、地方国有企业债务、商业不良贷款等或有隐性债务来源的风险进行监控与管理；(3)应通过设计标准化债务风险防控流程、制定差异化而有针对性的风险防控策略、完善政府性债务信息披露制度等提高地方政府对各类债务风险的预警响应速度和应急管理能力。不足之处在于，由于数据局限性而未能将所有或有隐性债务都纳入风险预警指标体系，今后随着违法违规类隐性债务数据的审计公告，以及社保缺口类隐性债务数据的官方公布或可合理估算，将进一步优化和完善预警指标体系。此外，目前尚缺乏更微观的市、县一级的相关实证与应用，今后如果数据可得，将进一步扩大样本以提高模型适用性。