箱包炸弹内爆作用下单层球面网壳结构的动力响应分析

李 丹 ，骆志远，夏芊文，邓勇军 ,2

(1. 西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2. 工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621010)

近年来，网壳结构等大空间公共建筑在我国得到广泛应用，而其作为地标性建筑物，人员往往较为密集，在恐怖主义全球化、网络化蔓延的大环境下，极易成为恐怖分子的袭击目标[1-2]，从而造成恶劣的社会影响。但国内外学者对网壳结构等大空间公共建筑的研究主要集中在强震以及冲击荷载作用下的稳定性能、失效模式及失效机理方面。虽然部分学者对钢框架结构在爆炸荷载作用下的响应行为开展了一些研究[3-10]，取得了一些研究成果，但不同结构形式的建筑在爆炸作用下的响应行为差异较大。而针对爆炸作用下网壳结构的研究，Su等[11]对带防爆墙的网壳结构在外爆下的动力响应展开研究，讨论结构参数以及防爆墙参数变化对网壳动力响应的影响，表明外爆炸下，塑性杆件主要分布在靠近炸点一侧的网壳内环区域。高轩能等[12]对柱面网壳在内爆作用下的动力响应进行研究，对影响结构响应的内外部因素进行了分析讨论，得出网壳结构转角区域杆件应力较高的结论。Zhai等[13]对网壳结构在内爆荷载作用下的泄爆措施进行研究，得到不同开洞率以及开洞位置与网壳结构动力响应的规律。孙振宇[14]采用杆件塑性应变百分率、平均塑性应变、最大节点位移3项响应指标，对外爆作用下的网壳进行损伤评估，揭示了网壳结构在外爆荷载作用下的整体刚度以及塑性发展规律。可以发现，国内外学者对网壳结构在爆炸作用下的研究方式及内容主要是通过网壳在爆炸荷载作用下的响应现象，研究其在内爆下的泄爆措施或外爆下的防护措施，对其响应机制或机理的分析较少，而且研究成果主要是针对网壳结构遭受汽车炸弹(大当量外爆)和军事打击(局部高强冲击、大当量内爆)两种典型袭击方式。然而，在我国对炸药的严格管制以及良好的国际形势下，此类建筑遭受汽车炸弹或军事打击的可能性并不大。箱包炸弹相对较小的爆炸当量，能够制造一定的杀伤力和恐怖气氛，得到恐怖分子的青睐[15-16]。因此，迫切需要开展网壳结构等大空间公共建筑在箱包炸弹内爆作用下的响应行为研究，获取其动力响应规律。

为此，本文采用杆件轴向应力、塑性应变、节点位移等响应指标[17]，研究网壳结构在箱包炸弹内爆作用下的特征响应规律，获取炸点位置系数与杆件塑性应变百分率之间的定量关系，进而揭示网壳结构在箱包炸弹内爆作用下的关键薄弱部位及形成机制，为网壳结构抗爆防护设计提供合理参考。

1 模型介绍

1.1 数值计算模型建立

模型跨度40 m，矢跨比1/5，下部结构高度10 m，模型组成、材料类型及参数如表1所示。支座节点固定铰支，围护结构与钢柱之间采用铆钉连接。屋面荷载、杆件、节点自重根据实际受荷面积，以集中质量的形式，将1.8 kN/m2的均布荷载，平均分配到网壳上部的各个节点上。采用MAT_SIMPLIFIED_JOHNSON_COOK本构模型模拟钢材及蒙皮材料在爆炸荷载下的力学行为，参考文献[11]，通过J-C方程建立应变率与屈服应力的函数关系如下式

(1)

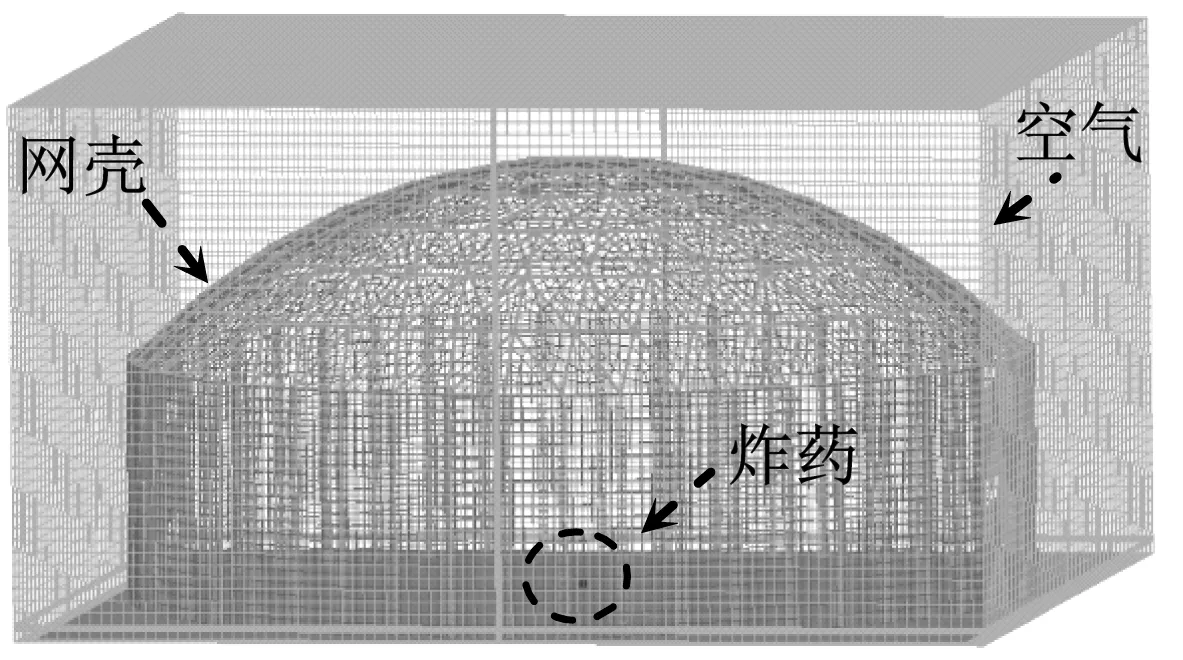
图1 有限元模型Fig.1 Finite element model

表1 模型参数

空气采用MAT_NULL和EOS_LINEAR_POLYNOMIAL状态方程模拟，其关系式如下所示

P=C0+C1u+C2u2+C3u3+(C4+C5u+C6u2)E

μ=ρ/ρ0-1

(2)

式中：P为空气压力；E为每单位基准体积空气内能；ρ为当前空气密度;ρ0为基准空气密度，具体取值见表2。

炸药采用MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程模拟，其形式为

(3)

式中：P为静水压力；V为相对体积；E为单位体积炸药的初始内能；ω、A、B、R1、R2为材料常数。

空气尺寸44 m×44 m×22.1 m，空气及炸药均使用solid164单元，网格大小参考文献[18]选用20 cm。采用流固耦合方式模拟冲击波与结构之间的相互作用。

表2 空气材料参数

表3 炸药的材料参数

1.2 模型正确性验证

本文选取部分经典的超压经验公式进行计算[19-25]，将数值模拟结果与经验公式结果进行比对。图2将数值模拟得到的冲击波峰值超压随比例距离变化曲线与有关文献经验公式进行对比。从图2可以看出，可以看出，各经验公式在比例距离大于2.5 m/kg1/3时，爆炸冲击波超压值差异较小，本文爆炸比例距离一般较大，因此本文数值模型参数选取是较为合理的，可为后面的数值模拟分析提供较为准确的数据。

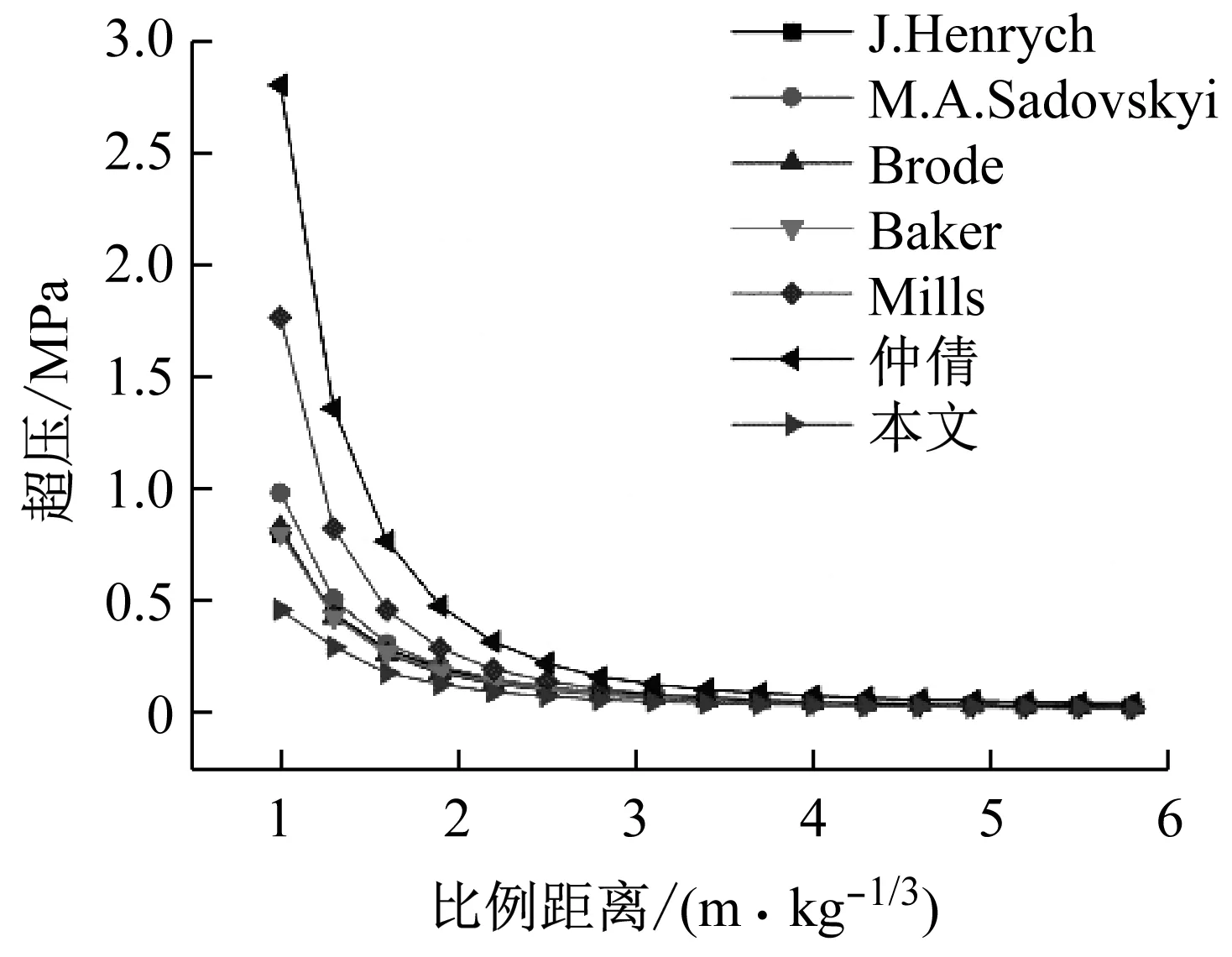
图2 冲击波峰值超压随比例距离变化曲线Fig.2 The varying curve between shock wave peakoverpressure and scaled-distance

2 内爆炸工况设计

2.1 爆炸当量及炸点高度

美国ATF[19]组织专家人员研究了各类箱包炸弹的爆炸当量，并对其可能携带的炸药能力进行了分类，如表4所示。

表4 箱包炸弹携带能力

因此，结合国内形势，本文将网壳结构可能遭受的最大爆炸当量限定在典型箱包炸弹范畴。即爆炸当量在23 kg左右，炸点高度依据市面箱包的规格尺寸，按照其长宽高不超过1.5 m设定。

2.2 最不利内爆炸类型

箱包炸弹内爆时，网壳结构存在两种典型的损伤破坏类型，即泄爆型破坏和非泄爆型破坏。炸点位置靠近结构中心区域时，围护结构不发生破坏，导致爆炸冲击波在结构内部不断的反射、叠加、绕射，结构整体发生非泄爆型破坏；当炸点位置位远离结构中心区域时，结构局部区域承受较大冲击波能量导致维护结构破坏，释放一部分冲击波能量，结构发生非泄爆破坏。由于箱包炸弹炸点高度相对于网壳结构高度而言较低，因而网壳结构损伤破坏类型的转变主要取决于炸点水平位置的变化。以网壳中心为起始试算点，按每1 m进行炸点位置偏离，发现炸点位置在17 m处为非泄爆型破坏，炸点位置在18 m处发生泄爆型破坏，因此确定临界位置在17～18 m之间，然后在这个区间内按每0.1 m进行差值计算，最终确定网壳结构由非泄爆型破坏向泄爆型破坏转变的临界炸点位置P，即位于离网壳中心17.8 m的圆周上(图3粗实线所示)。

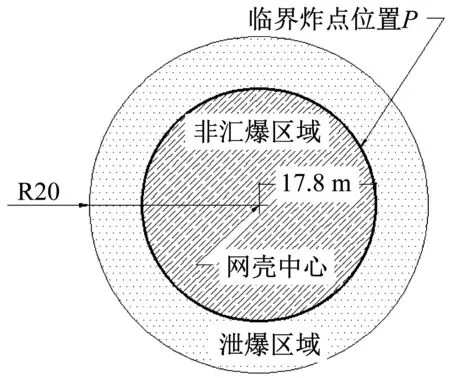
图3 临界炸点位置PFig.3 The critical location P of bomb

2.3 工况布置

考虑到网壳的对称性，本文仅设置网壳半跨炸点可能的分布区域。以地面网壳中心为原点，地面作为X-Y平面，网壳高度为Z轴建立3D直角坐标系，等效TNT当量25.46 kg。按网壳半跨每2.5 m设置1个水平炸点、3种炸点高度(0.5/1.0/1.5 m)，共计24种工况，见图4所示。

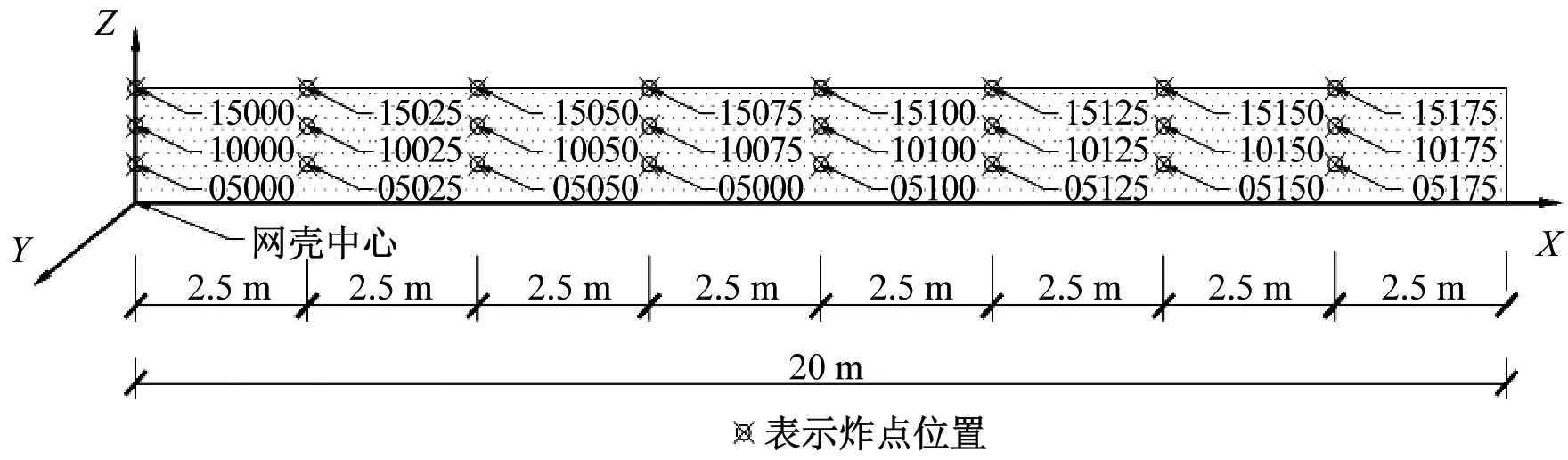
图4 工况布置示意图Fig.4 The schematic diagram of condition arrangement

工况编号规则如下：“05175”，前两位数“05”代表炸药中心离地面高度，后三位数“175”代表炸药中心离网壳中心水平距离。即“05175”表示炸药中心距离地面0.5 m，偏离网壳中心17.5 m。

3 动力响应分析

采用文献[14,17]的特征响应指标，研究网壳结构在典型箱包炸弹内爆作用下的特征响应规律。从网壳内部流场分布特征的角度出发，分析其响应机制及机理，以便揭示网壳结构在内爆作用下的易损薄弱部位。

3.1 杆件轴向应力

凯威特单层球面网壳由环杆、肋杆、斜杆3种杆件类型构成。因此，选取代表性杆件环杆R1/R4、斜杆R2/R5、肋杆R3/R6研究其轴向应力响应，具体选取位置如图5所示。

图6为中心爆炸下网壳杆件轴向应力响应时程曲线。

图5 杆件选取示意图Fig.5 The schematic diagram of member select

图6 工况15000轴向应力时程曲线Fig.6 The axial stress-time curve of condition 15000

从图6中可看出，3类杆件轴向应力呈现以零点为平衡位置，上下振荡并不断衰减的规律。环杆R1最大峰值轴向应力达到269 MPa，与斜杆R2以及肋杆R3相比，其轴向应力时程曲线呈高频率、高幅值的特点，而斜杆R2以及肋杆R3峰值轴向应力约为100 MPa，与环杆R1相比，其轴向应力时程曲线呈低频率、低幅值特点。

首先，为证明此种现象是否与杆件所处位置有关，本文继续提取图7中所示的(7/8/9)、(10/11/12)、(13/14/15)、(16/17/18)、(19/20/21)五组杆件进行轴向应力分析。

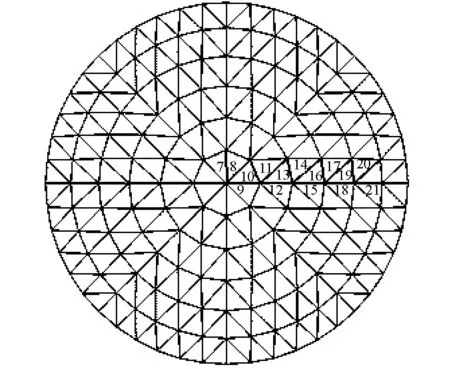
图7 杆件选取示意图Fig.7 The schematic diagram of member select

(a) 杆件7/8/9轴向应力时程曲线(b) 杆件10/11/12轴向应力时程(c) 杆件13/14/15轴向应力时程曲线

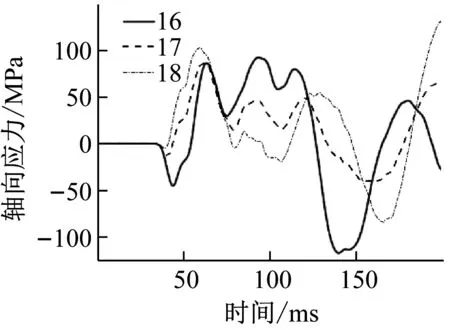
(d) 杆件16/17/18轴向应力时程曲线(e) 杆件19/20/21轴向应力时程曲线图8 杆件轴向应力时程曲线Fig.8 The axial stress-time curve of member

从图8(a)～(e)所示5组杆件的轴向应力时程曲线可见，越靠近网壳支座，环杆轴向应力时程曲线与其余两类杆件差异越大。从倒数第三环开始(见图8(c)-图8(e))，环杆轴向应力与其他两类杆的轴向应力相比而言频率高、幅值大。由此证明“环杆效应”特征与环杆所处的位置有关，且主要位于网壳的倒数1～3环区域。

其次，为进一步探究“环杆效应”的产生原因，提取网壳内部流场分布特征进行以下分析。可以发现，34 ms冲击波还未与环杆R1/R4接触，此时环杆R1/R4在网壳顶部受到的冲击波作用下，承受轴向压力作用(见图9(a))。51 ms地面反射形成的马赫波与沿网壳屋盖传来的冲击波在支座处汇聚(见图9(b))。随积聚程度增加(见图9(c))，环杆逐渐展现出前述图6所示的高频率、高幅值特点，杆件轴向拉力逐渐增大。随后冲击波逐渐在柱脚积聚，杆件轴向拉力减小(见图9(d))。此种“环杆效应”是由于支座附近积聚的冲击波导致，其积聚区域在网壳倒数1～3环区域。

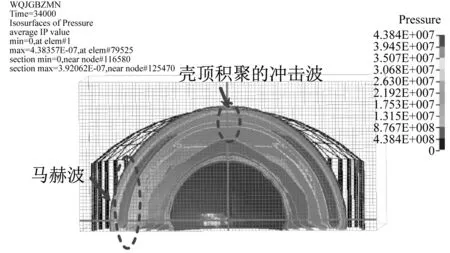
(a) 34 ms网壳内部流场分布(b) 51 ms网壳内部流场分布

(c) 63 ms网壳内部流场分布(d) 94 ms网壳内部流场分布图9 网壳结构内部流场分布Fig.9 The internal flow field distribution of reticulated shell

继续分析偏心爆炸工况(15150)杆件轴向应力特征，提取其轴向应力时程绘于图10中。

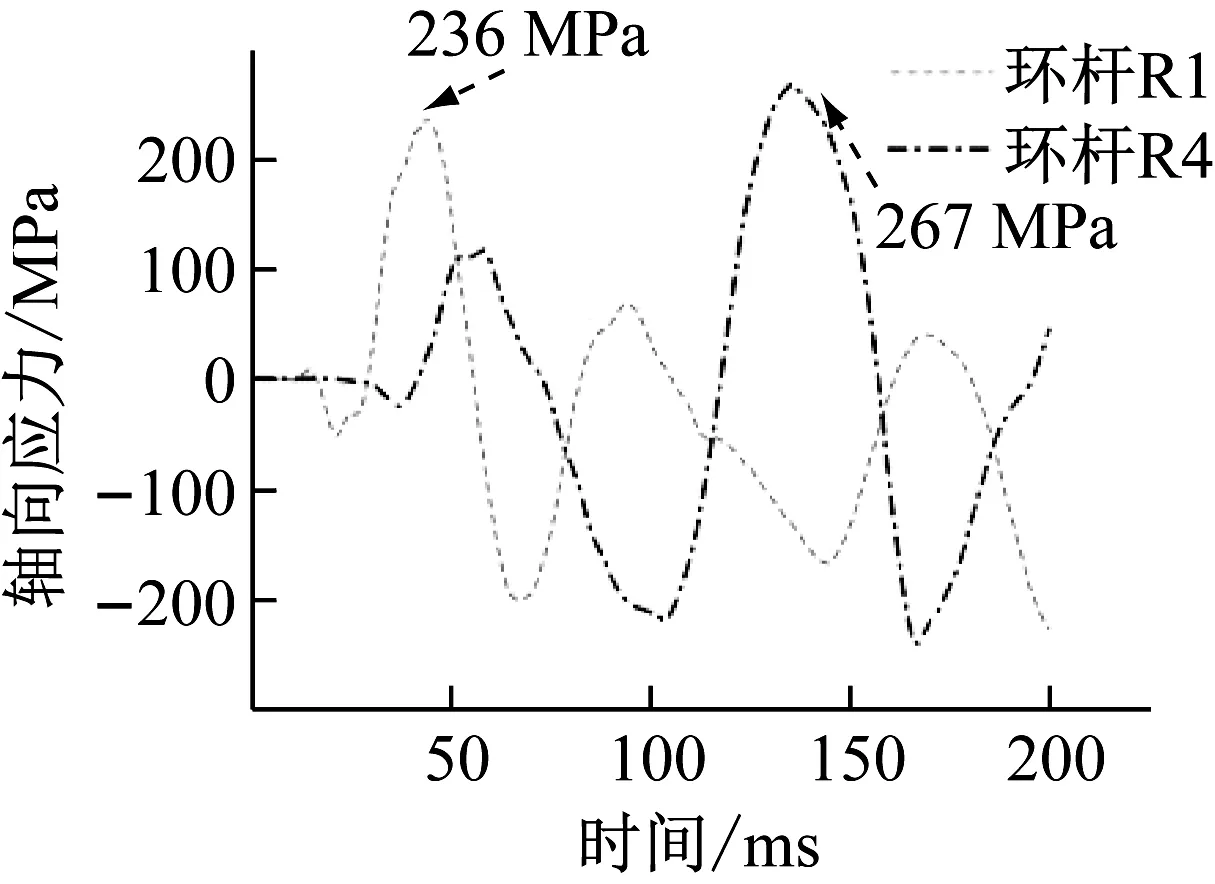
(a) R1/R4轴向应力时程曲线(b) R2/R5轴向应力时程曲线(c) R3/R6轴向应力时程曲线图10 工况15150轴向应力响应时程曲线Fig.10 The axial stress-time curve of condition 15150

可以发现，偏心爆炸下，环杆的峰值轴向应力水平仍较高(见图10(a))，且靠近炸点处杆件R1/R2/R3，比远离炸点处杆件R4/R5/R6峰值轴向应力低(见图10(a)～(c))。靠近炸点处的杆件，轴向应力响应主要是由于冲击波的直接作用以及柱脚积聚的冲击波沿围护结构向上传播，并在支座附近积聚导致。而远离炸点的杆件，是由于靠近炸点位置积聚形成的冲击波沿网壳上部屋盖传播到网壳结构另一侧，与入射波以及地面反射形成的马赫波积聚造成。远离炸点处强度更高，杆件轴向应力较高。

3.2 塑性应变

本节通过杆件塑性应变百分率变化规律以及塑性应变杆件随炸点位置变化的分布特征两方面，进一步探讨典型内爆炸工况下单层球面网壳结构的动力响应机制和结构塑性发展程度。

塑性应变百分率是指进入塑性应变的杆件单元数量占总杆件单元数量的比例。图11为3种典型炸点高度下，塑性应变百分率随炸点水平位置的变化规律。

从图11可以发现，位置处于中心爆炸处，塑性应变百分率最小值为46.54%；随炸点水平偏心距离的增大，杆件塑性应变百分率逐步增大，在网壳半跨3/4处(偏心15 m)处，塑性应变百分率达到最大值，为85.03%。这是因为偏心爆炸下，随着炸点偏心距的逐渐增大，冲击波在炸点一侧支座处的局部增强效应越明显，导致冲击波沿上部网壳屋盖从炸点一侧向网壳另一侧传播的过程中，携带的能量增多，在此过程中，冲击波携带的大部分能量被网壳杆件、屋面围护结构以塑性变形、屋盖位移的形式耗散吸收。因此，网壳杆件塑性应变百分率逐渐增大。而中心爆炸下，爆炸能量主要以入射波形式均匀作用在上部网壳结构，冲击波在网壳结构局部的增强效应削弱，从而塑性应变百分率相对较低。

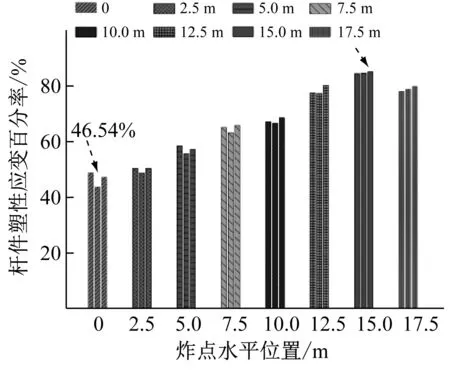
图11 塑性应变百分率变化规律Fig.11 The change law of plastic strain percentage

而网壳杆件的塑性应变百分率可以一定程度反映网壳结构的响应水平以及损伤情况。为进一步研究炸点水平位置与杆件塑性应变百分率之间的关系，本文参考文献[19]对结构空间高度系数的定义方法，定义炸点位置系数ξ。ξ为炸点所处位置(L,0,h)绕网壳中轴线K旋转180°所围成的半圆柱体积占整个炸点所处平面以下部分网壳半跨体积的比值，如图12所示。

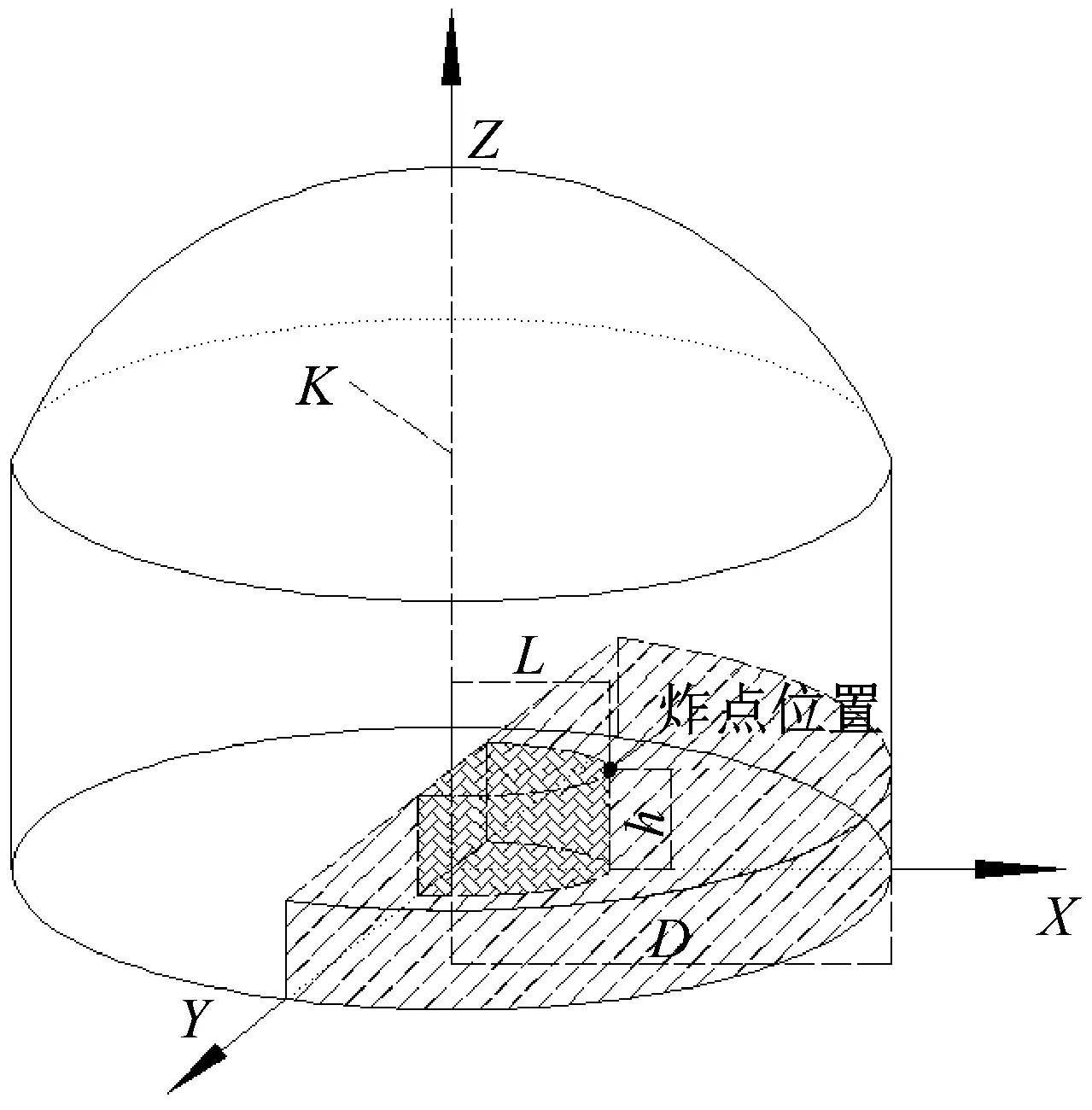
图12 炸点位置系数示意图Fig.12 The schematic diagram of blast position coefficient

炸点位置系数ξ表达式如下

(4)

式中：D为网壳半跨长度；h为炸点高度。依据各工况杆件塑性应变百分率，运用origin软件，拟合炸点位置系数ξ与杆件塑性应变百分率γ之间的表达式如下

γ=48.7+113.8ξ-77.7ξ2-22.9ξ3

(5)

根据式(4)，通过给出箱包炸弹炸点位置即可得到炸点位置系数ξ，进而通过式(5)大致得到网壳杆件的塑性应变百分率。塑性应变百分率随炸点位置系数变化的规律如图13所示。

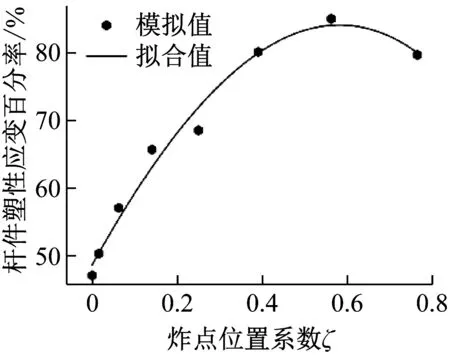
图13 塑性应变百分率随炸点位置系数变化规律Fig.13 The change law of plastic strain varies with theblast position coefficient

为继续研究内爆炸下网壳结构塑性应变杆件随炸点水平位置变化的分布特征，本文提取4种不同炸点水平位置下，杆件的塑性应变分布图进行比较分析，如图14所示。

(a) 15000工况(b) 15100工况

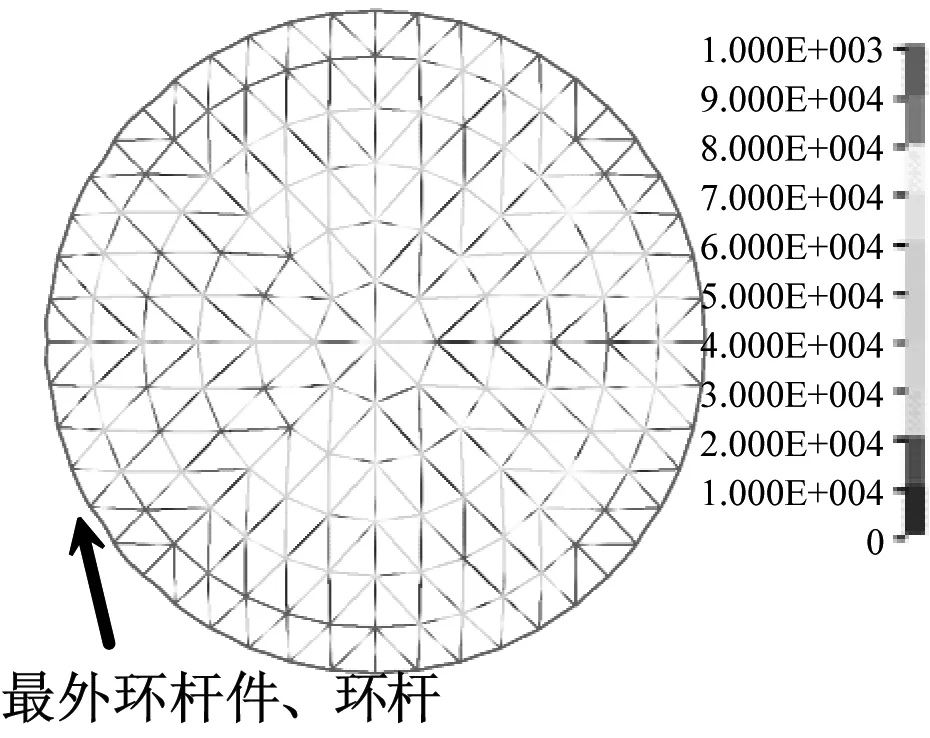
(c) 15150工况(d) 15175工况图14 塑性应变杆件随炸点水平位置变化的分布特征Fig.14 The distribution of plastic member with variedhorizontal blast position

可以发现，各工况下支座附近杆件全部进入塑性应变状态。当炸点位于[0-15)m区间内时(图14(a)～(b)所示)，网壳内环塑性杆件主要分布在与炸点相反的一侧。而当炸点位于(15-17.5]m区间内时(图14(d)所示)，网壳内环塑性杆件主要分布在炸点一侧。当炸点位于[0-15)m区间时，网壳的塑性应变主要是由于沿网壳屋盖传播的冲击波与地面反射形成的马赫波在远离炸点的支座处叠加造成。而当炸点处在(15-17.5]m区间时，入射冲击波的直接作用产生近炸点处较高的网壳塑性应变，而近炸点支座处叠加的冲击波沿网壳屋盖传播到远离炸点的网壳另一侧的距离更长，远炸点处杆件塑形应变并不明显。

各工况下，环杆塑性应变百分率均较高。这是因为冲击波在沿网壳屋盖传播的过程中，冲击波与环杆的直接作用面积更大，因而环杆塑性应变率更高。

3.3 最大节点位移

节点位移反映网壳结构在抵抗爆炸作用时的刚度水平。本文中的节点位移是指节点3个方向的合位移。各工况最大节点位移随炸点位置的变化如图15所示。

图15 最大节点位移变化随炸点位置变化规律Fig.15 The change of maximum node displacement with variedblast position

可以看出，最大节点位移对炸点水平位置的变化较为敏感。中心爆炸3种高度下最大节点位移均值为12.31 cm，而远离中心12.5 m时最大节点位移为34.79 cm。虽然最大节点位移值相差较大，但位移最大节点的分布区域却大致相同，均处在网壳倒数第二环杆件附近，如图16(a)、(b)所示。表明此区域为网壳结构在内爆炸荷载作用下刚度较为薄弱的区域。

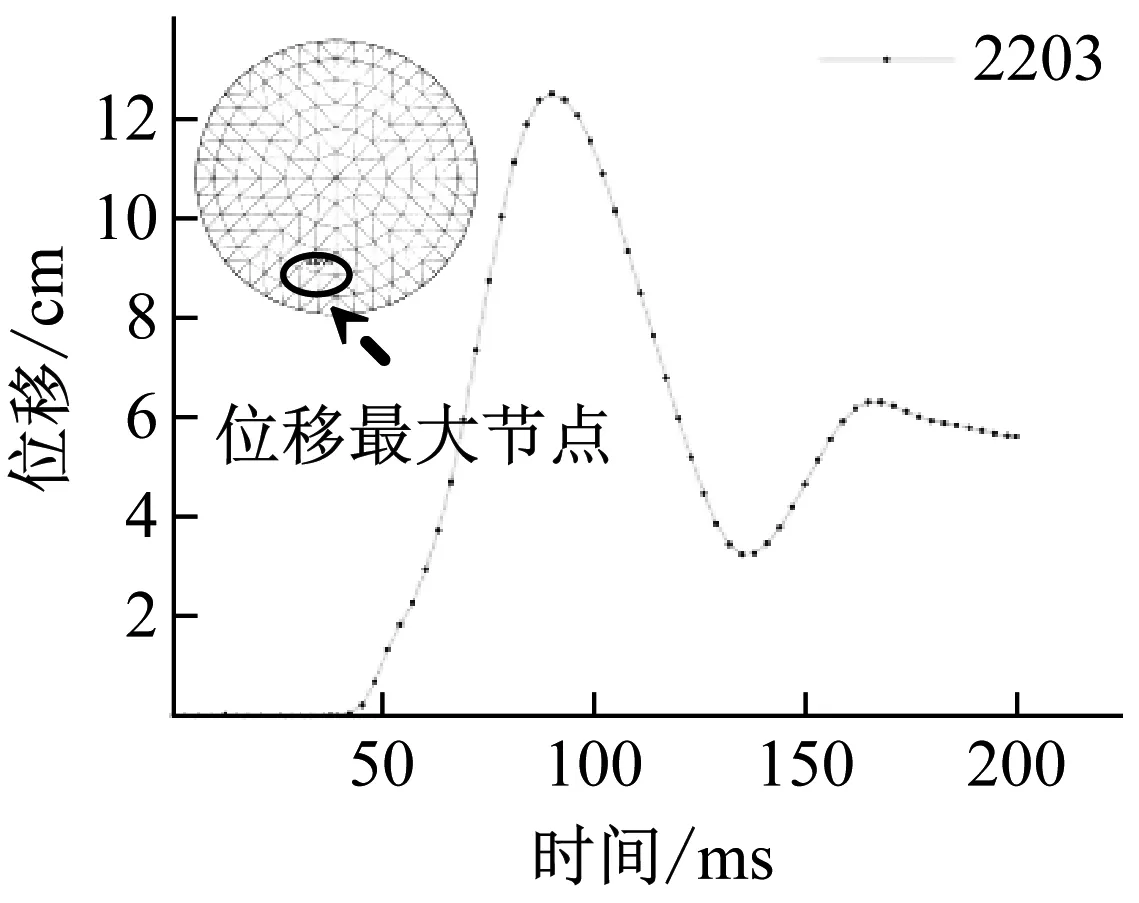
(a) 工况15000

(b) 工况15150图16 位移最大节点的分布位置Fig.16 The distribution of maximum displacement node

因此，在对网壳结构进行抗爆设计时，应尽量增大倒数第二环附近区域的刚度水平，避免此处杆件在内爆荷载作用下，产生较大塑性变形或断裂，引起网壳结构局部塌陷，甚至整体倒塌的二次事故发生。

通过前述对网壳特征响应现象的分析可知，由于内爆炸下冲击波局部的增强效应以及冲击波传播路径对环杆的影响，凯威特K8单层网壳结构在箱包炸弹内爆炸下的易损薄弱部位主要有柱脚、网壳支座附近区域以及网壳环杆3部分。

4 结 论

本文运用ANSYS/LS-DYNA软件对凯威特K8单层球面网壳结构遭受典型箱包炸弹内爆作用下的动力响应展开研究，得到以下几点主要结论：

(1) 支座处积聚的冲击波，沿网壳屋盖向网壳中心传播的过程中，其与环杆的直接作用面积更大，导致环杆塑性应变率较高，且越靠近网壳支座的环杆，轴向应力越大，材料冗余度越低。

(2) 炸点位置不同，网壳内部冲击波流场分布、冲击波传播路径以及冲击波与网壳的作用过程存在明显差异，因而特征响应随炸点位置改变变化较大，各特征响应大致在网壳半跨3/4处达到极值。

(3) 网壳结构在箱包炸弹内爆下的易损薄弱部位主要有3部分，即由冲击波的局部增强效应导致的网壳支座附近杆件、柱脚部分，以及由冲击波传播路径影响导致的网壳环杆部分。