穿孔式双浮体装置水动力及波能转换特性研究

周亚辉，杨兴林，周效国，张万超

(1. 江苏科技大学 能源与动力学院，江苏 镇江 212003； 2. 江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

一直以来，能源作为世界经济、科技等方面的动力支柱，是人类社会在发展过程中考虑的重要对象[1-3]，随着人类社会经济和人口数量的爆发式增长，能源问题日益突出，日渐成为制约人类文明发展速度的瓶颈，新能源逐步成为人类发展的新目标。目前虽然太阳能、风能等新型能源已经迅速发展，但它们占陆地面积过多，不能有效地利用好一些偏远地区的陆地占地，于是人们开始着眼于占地球面积71%的水资源中的新型能源[4]，尤其是具有广泛开发价值的海洋能。海洋能包括波浪能、潮汐能、温差能量、洋流能量、盐差能量等。自上世纪末，从海洋中获取能量成为替代能源的主要方式，提高波浪能在安全范围内的俘获宽度比也相应受到越来越多的关注。

目前，单浮体式波浪能转换装置已处于广泛研究中[5-6]，而如今的研究热点是如何将其应用到深水海域并高效地获取能量，比如改善动力输出系统的能量转换特性[7]。但是相较于更加复杂的动力输出系统，在现有的单浮体装置的基础上，设置不同形式载体，进而构成双体式波能装置并将其运用于深水，提高捕获效率的同时，扩大运用范围，受到更多的关注。研究深水中加装载体对俘获宽度比的影响，对其他波能转换形式的相关研究具有重要借鉴意义。

阻尼板是海洋工程中常用的稳性辅助构件[8-10]，但是将其应用于波浪能装置中的很少[11-16]，大部分研究中将阻尼板当作悬浮在水中固定不动的反应板来使用，从而忽略了阻尼板与浮子之间的相互水动力作用。事实上，阻尼板存在会使浮体周围流场的水动力边界条件发生改变[17]，浮子与阻尼板的相互作用同样会对系统的波能转换特性产生很大的影响[18]，在一定程度上促进了系统的波能转换能力[19]。但由于阻尼板悬浮于水中，垂直方向投影面积一般较大，加之其附加水质量作用对阻尼板强度要求较高，为此本文在前人研究的基础上，提出穿孔阻尼板，针对不同开孔半径下阻尼板对吸能浮子水动力及系统能量转换能力的影响展开研究，为后续深水浮式波浪能发电装置的研究提供借鉴和依据。

1 理论分析

1.1 波能转换模型

假定圆柱浮体通过 PTO 系统与悬浮系泊阻尼板连接，在波浪作用下作相对往复垂荡运动，激活阻尼器进而对外做功，由此构成一个复杂的双自由度振动系统，其振动模型可以表示如图1所示，其中ch和kh分别表示由水动力产生的等效阻尼和刚度系数，cp为PTO阻尼系数。

假定该系统在静水中处于静平衡状态，在线性波作用下，将振子瞬时位置与平衡位置的相对位移定义为其位移，同时假定入射波浪是线性微幅波。根据牛顿第二定律，波浪作用下该双体振动系统的受迫运动方程可以表示为

(1)

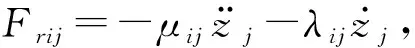
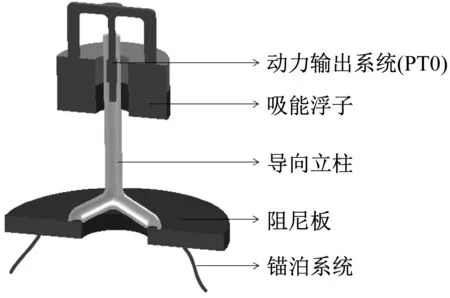
(a) 装置简图

(b) 振动模型图1 波能转换振动模型Fig.1 The oscillating model for the WEC

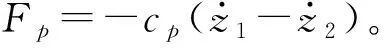
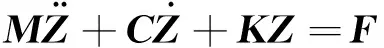
(2)

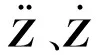
M=[aij],C=[bij],K=[cij],

Z={z1,z2}T,F={Fe1,Fe2}T,

(3)

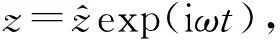
(4)

求解上述线性方程组，得到浮子与载体的运动位移，结合阻尼器对外做功方式，可得由于浮子相对载体运动激励阻尼器对外做的功，具体可以表示为

(5)

其中

det[N(iω)]=N11N22-N12N21=(a+ib)cp+

c+id

(6)

则波能俘获功率可以表示为

(7)

R表示取复数实部，由于(N22+N12)F1-(N11+N21)F2与PTO系统参数(阻尼系数 )没有关系，因此当波浪能俘获功率对阻尼系数的导数为0时，得到的阻尼系数及对应的俘获功率即为最优的，具体表示为

cp,opt=[(c2+d2)/(a2+b2)]0.5

(8)

1.2 水动力模型

本文波能装置工作水域深度为h，获能结构为半径为R1，吃水为d1的漂浮圆柱形浮子，载体为与浮子共轴的浸没于浮子下方的阻尼圆盘，定义其半径为R2，浸水深度为d2，厚度为t。装置中PTO系统安装在立柱内部，连接浮子于阻尼板，不会对系统水动力产生影响。在柱坐标系(r,θ,z)下，为便于描述波能装置在波浪中的流场特性，定义水平面roθ在静水面上，oz轴垂直向上，由此得到的浮体结构布置及对应的流域划分如图2所示。

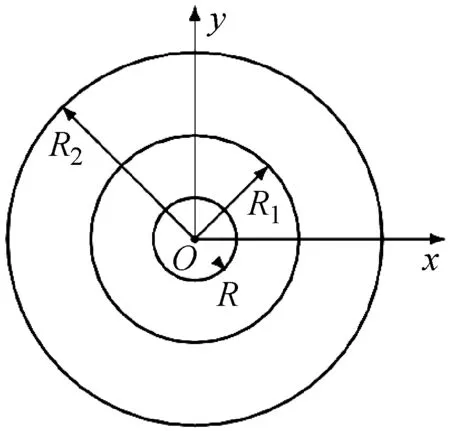
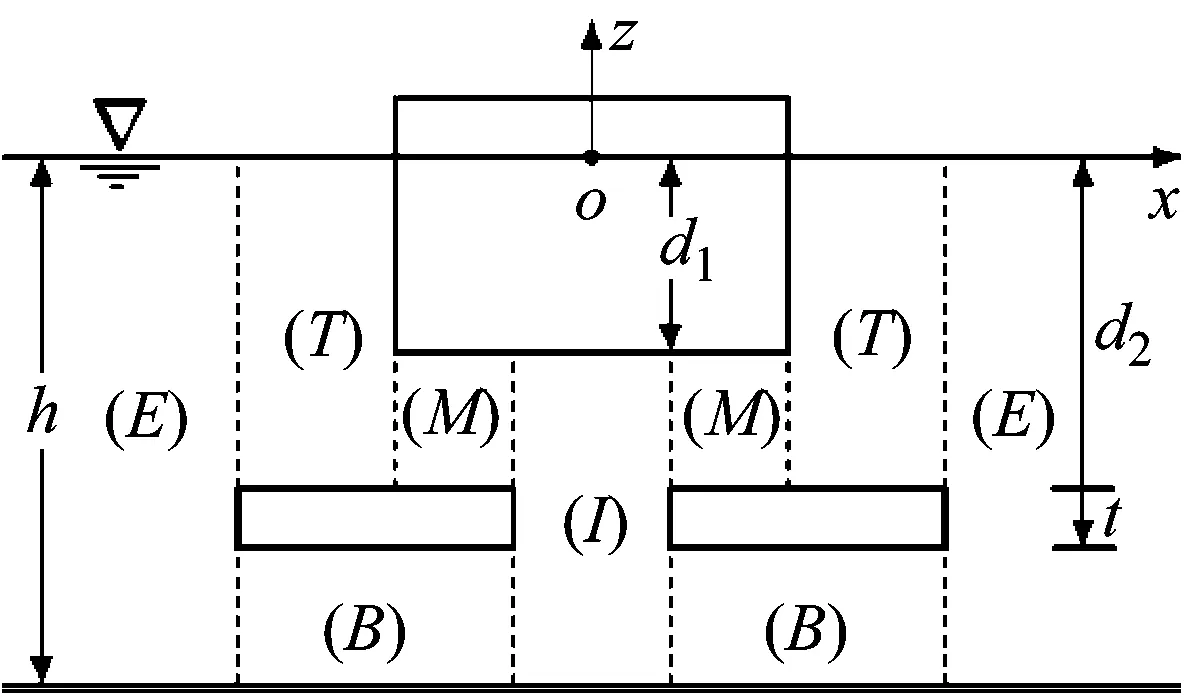
图2 带穿孔阻尼板的波能装置简图及流域划分示意图Fig.2 Sketch of the wave energy device with perforateddamping plate

根据线性波理论，流域中的速度势可以提出其时间因子e-iωt，由此得到的空间速度势Φ(r,θ,z)可以分解为入射势、绕射势和辐射势，具体可以表示为

Φ(r,θ,z)=Φ0(r,θ,z)+Φ7(r,θ,z)+

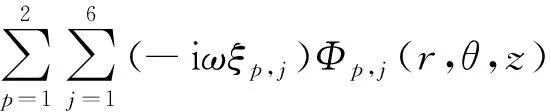
(9)

式中：Φ0(r,θ,z)表示入射波的速度势；Φ7(r,θ,z)表示散射速度势，它们共同组成绕射速度势ΦD(r,θ,z)；ξp,j表示浮体p做j模态的运动振幅；Φp,j(r,θ,z)表示由该模态运动产生的辐射速度势，由于本文仅考虑垂荡运动，则速度势Φp,j(r,θ,z)和位移幅值ξp,j可以分别用Φp(r,θ,z)和ξp代替。上述空间速度势需要满足域内Laplace方程、自由面条件、海底不可穿透条件及远场辐射条件，具体可以表示为

2Φ=0

ω2Φ-g∂zΦ=0z=0,r≥R1

∂zΦ=0z=-h

(10)

此外，速度势还需要满足物面条件

∂nqΦp=δpqnq,∂npΦD=0

(11)

式中：下标p,q(p,q=1,2)表示浮体编号；δpq表示克罗内克符号。设入射波波幅为ξ0，沿x轴正向传播可表示为

(12)

ε0=1,εl=2(l≥1)

(13)

式中：k0为波数；εl为诺伊曼的符号；g为重力加速度；Jl为l阶第1类Bessel函数。基于文献[16]的特征函数展开及边界匹配的势流半解析方法，可以得到流场速度势函数，进而基于伯努利方程可以得到作用在浮子和阻尼板上的波浪载荷。分别将浮子和开孔阻尼板定义为1和2，其受到的波浪激励力可以表示为

(14)

由于自身运动受到的辐射作用力可以表示为

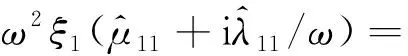
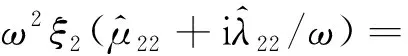
(15)

由于其它浮体运动产生波浪而受到的作用力可以表示为

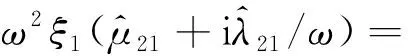
(16)

其中下标表示后面浮体运动对前面浮体产生的影响，上述方程中速度势上标分别对应图2中的子流域。为便于描述，本节水动力计算结果均无因次表述所示

波浪激励力：

(17)

辐射作用力：

(18)

式中：i,j=1,2分别表示浮子和阻尼板；A0为入射波波幅，带上标记的激励力及水动力系数为计算得到的结果。

2 水动力特性

本论文针对考虑开孔阻尼板的双浮体式波能装置展开研究，重点分析不同开孔半径下阻尼板对浮子水动力及系统波能俘获能力的影响。为便于研究，本文给定工作水深为h=50 m，获能圆柱浮子半径R1=4 m、吃水d1=5 m，定义开孔阻尼板的外半径为R2，并有R2/R1=1.5，阻尼板浸没深度为d2，开孔半径为R，由于本文仅考虑阻尼板开孔尺寸对双浮体装置的垂荡方向上的影响，将阻尼板厚度t给定为0.2 m。本文分别从波浪激励力、辐射作用力(附加质量和辐射阻尼)几个方面来探讨阻尼板不同开孔半径下，浮子与阻尼板的相互作用水动力特性。

2.1 波浪激励力

图3描述的是无开孔阻尼板在给定外半径，考虑不同浸没深度条件下，浮子与阻尼板受到的波浪激励力。

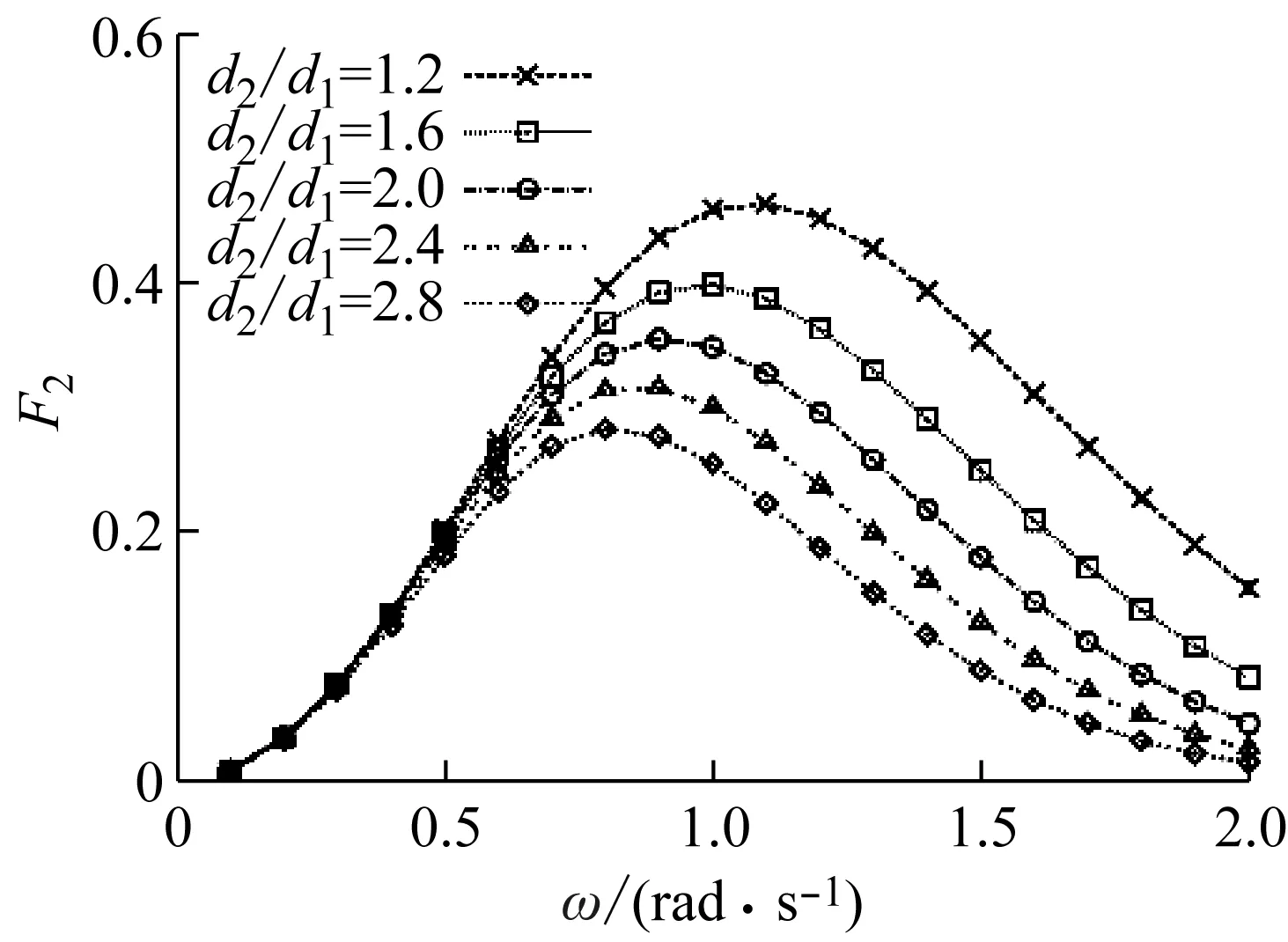
图3 不同浸没深度下的无因次垂荡波浪激励力Fig.3 Non-dimensional wave excitation forces with differentsubmerged depth

由图3可知，阻尼板的浸没深度对浮子的波浪激励力影响甚小，但在高频部分对自身的波浪激励力影响较大，且阻尼板自身激励力的峰值对应频率会随着浸没深度的增加而右移。为此在论文后续研究中，为了不考虑浸没深度的影响，仅研究开孔半径对浮子及阻尼板水动力的作用，给定阻尼板浸没深度为d2/d1=1.6。

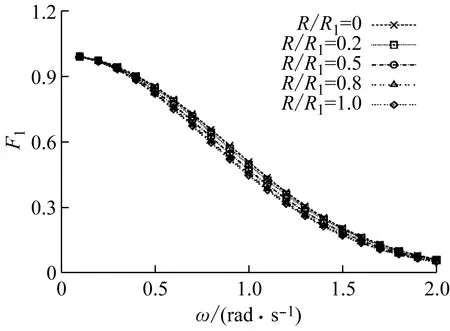
图4 不同开孔半径下的无因次垂荡波浪激励力Fig.4 Non-dimensional wave excitation forces with differentopening radius

考虑阻尼板开孔后浮子与阻尼板的波浪激励力如图4所示，从图中可以看出，给定阻尼板外半径后，浮子受到的波浪激励力几乎不随阻尼板的开孔半径变化，但会随着频率的提高呈下降趋势。但是同等条件下，阻尼板受到的波浪激励力随着开孔半径变化有较大差别，具体表现为开孔半径增大，阻尼板的波浪激励力在整个计算频域范围逐渐减小，同等深度下开孔半径的变化对峰值对应的频率几乎没有影响。

2.2 辐射作用力

在阻尼板不同开孔半径情况下，双浮体装置受到本身受迫振荡产生的辐射作用力，还受到浮体之间的相互作用辐射作用力，根据其载荷特性分别从附加质量和辐射阻尼两方面进行研究。

图5依次描述的是浮子、阻尼板以及它们之间的耦合无因次附加质量。从图中可以看出，开孔半径对浮子、阻尼板及其耦合附加质量影响比较明显，随着开孔半径增大，浮子和阻尼板的附加质量在整个计算频率范围内均减小，说明阻尼板开孔削弱了浮子及阻尼板的辐射波能量，且半径越大削弱的越厉害；但它们之间的耦合附加质量绝对值随着开孔半径增大而减小，这是由于开孔后浮子自身垂荡产生的辐射波通过开孔向下传播，而由于阻尼板开孔，产生较少量的辐射波，对浮子的作用也很小。

图5 不同开孔半径下浮子与阻尼板的无因次垂荡附加质量Fig.5 Non-dimensional added mass in heave of the buoy and damping plate with different opening radius

不同开孔半径阻尼板下，浮子、阻尼板及它们之间的耦合无因次辐射阻尼计算结果如图6所示。同样的，随着阻尼板开孔半径增大，浮子和阻尼板由自身振荡产生的辐射阻尼均减小，但阻尼板的减小幅度更加突出。在计算频率范围内，辐射阻尼的绝对值均随着频率先增大后减小，值得注意的是，开孔半径的变化不会改变峰值处对应的频率。此外，耦合辐射阻尼的绝对值也是随着开孔半径增大而减小，结合附加质量的变化趋势，可以说明浮子与阻尼板之间的相互水动力干扰随着阻尼板开孔半径增大而减小，因此这种情况下很有必要进一步研究阻尼板开孔情况对浮子与阻尼板的运动特性影响。

3 波能转换特性

在水动力特性研究的基础上，已经发现阻尼板的开孔直接影响了浮子、阻尼板以及两者之间的水动力特性，为此，本节在此基础上首先研究浮子与阻尼板在不同开孔情况下的相对运动响应，进而根据之前的理论推导探讨不同工况下的最优PTO阻尼及对应的波浪能俘获效率。为了探讨不同开孔半径下浮子与阻尼板的运动响应，分别从自由振荡和有最优PTO阻尼两种情况下进行研究，具体结果如图7和图8所示。

在不考虑PTO阻尼时，可以发现开孔半径对浮子与阻尼板相对运动的影响主要体现在1.15～1.25 rad/s频率范围内，尤其在系统的固有频率附近，随着开孔半径增大，相对运动RAO是随之增加的，由此可以结合前面计算的波浪激励力及辐射作用力结果可以说明，阻尼板的开孔虽然不会增加浮子和阻尼板的波浪激励力，但它会减小浮子和阻尼板的辐射作用力，通过减少能量辐射损耗，有助于浮子和阻尼板的相对运动，而且还不会改变双浮体振动系统的固有频率。为了进一步说明阻尼板开孔带来的水动力和运动特性，根据前面的理论推导计算了考虑最优PTO阻尼后的浮子与阻尼板相对运动RAO，结果如图8所示。可以发现，尽管双浮体系统由于PTO能量输出，相对运动响应整体减小，但PTO阻尼的加入并不会改变阻尼板开孔带来的相对响应变化趋势，开孔半径越大，最优的相对运动响应更突出，也进一步说明阻尼板的开孔有助于双浮体系统的运动增强。

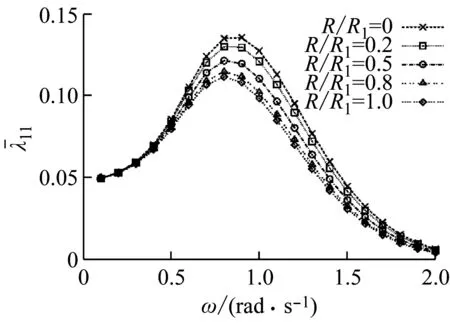
图6 不同开孔半径下的浮子和阻尼板的无因次辐射阻尼

图7 不同开孔半径下自由振荡时的相对响应振幅Fig.7 Relative RAOs of free oscillation with differentopening radius

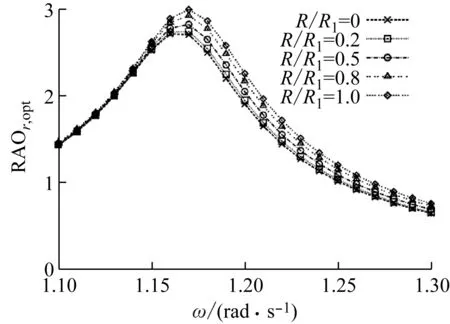
图8 不同开孔半径下的最优相对响应振幅Fig.8 The optimal relative RAOs with different opening radius

进一步地，在运动响应基础上计算研究了双浮体系统的最优PTO阻尼随着阻尼板开孔半径的变化特性如图9所示。从图中可以看出，阻尼板开口半径的增大会使最优PTO阻尼系数的峰值降低，阻尼系数峰值所对应的频率也会向频率高的方向移动。在低频和高频阶段，阻尼系数的差异会变小，而且都会向0接近，由此说明双浮体系统存在2个固有频率，而开孔半径会通过改变阻尼板自身固有频率进而改变系统固有频率。

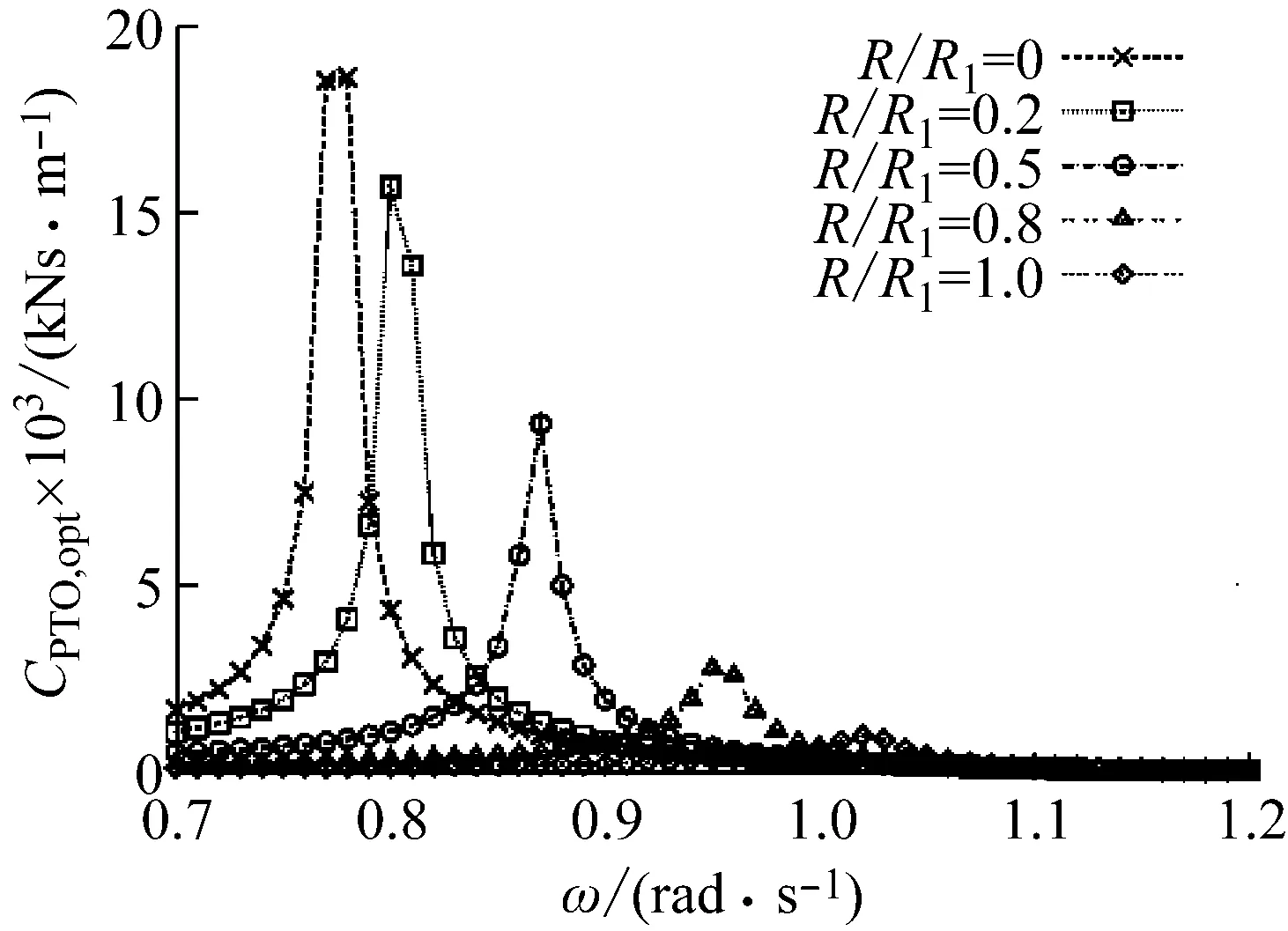
图9 不同开孔半径下的最优 PTO 阻尼Fig.9 The optimal PTO damping with different opening radius

图10 不同开孔半径下的最优俘获宽度比Fig.10 The optimal capture width ratios with differentopening radius

结合计算得到的最优PTO阻尼，不同开孔半径的双浮体装置的最优俘获宽度比也随之得到，结果如图10所示。从图中可以发现，最优PTO阻尼在计算频域范围内出现两个峰值，正好对应双浮体系统的两个固有频率。可以看出，阻尼板的开孔半径只能改变较小的固有频率，即与阻尼板固有频率靠近的那个，这是因为阻尼板开孔半径增大，其自身的固有频率逐步增大。另外，随着阻尼板开孔半径增加，两个固有频率逐步接近，虽然峰值也逐步减小，但也由此说明在不同的波浪环境中，可以通过设置开孔阻尼板，能有效改善双浮体系统的固有振动特性，从而更好的适应波浪环境，提高俘获宽度比。

4 结 论

本文基于线性波理论，通过特征函数展开和边界匹配的势流半解析方法，并结合多自由度振动理论，探索带孔阻尼板对获能系统水动力、运动响应及俘获宽度比的影响，得到如下结论：

(1) 阻尼板开孔半径对浮子的波浪激励力几乎没有影响，但会极大的减小阻尼板受到的波浪激励力；

(2) 阻尼板开孔尺寸对浮子、阻尼板及其耦合辐射作用力比较明显，随着阻尼板开孔半径增大，它们的绝对值均逐渐减小，浮子与阻尼板之间的相互水动力干扰也随着阻尼板开孔半径增大而减小；

(3) 浸没阻尼板使系统出现两个耦合共振频率，开孔半径会增加阻尼板自身固有频率进而影响系统固有频率；

(4) 阻尼板开孔半径增大有助于浮子与阻尼板的相对运动，而且通过阻尼板开孔能有效促进双浮体系统对波浪的适应性，提高系统的俘获宽度比。

研究结果可为深水波浪能利用的工程应用提供理论基础，为后续振荡浮子式波浪能发电装置优化提供依据。