动水压下减震连续梁桥随机优化及减震性能研究

马安财,谭 平,王社良,周福霖,

(1.西安建筑科技大学 土木工程学院，西安 710055； 2.广州大学 工程抗震减震与结构安全教育部重点实验室，广州 510405)

近年来，我国跨海桥梁的建设呈现出空前的增长趋势。跨海桥梁所处的荷载环境极为复杂，要同时承受地震、波浪、强风等多种荷载作用，为了提高跨海桥梁地震和波浪耦合作用下的安全性能，发展减震技术具有十分重要的工程意义[1]。

跨海桥梁地震响应分析中需要考虑流体-结构相互作用，对于直径较小的桥墩，国内外研究者主要采用简化或改进的Morison方程来描述水体对桥梁的动水压力[2-3]，以此来反映流固耦合相互作用。Yamada等[4]采用修正的Morison方程计算了动水压力，对地震和海浪激励下近海桩柱结构上的动力响应进行了分析；高学奎等[5]在简化Morison方程的基础上采用附加水质量考虑水的影响；赵秋红等[6]对比了各国规范中动水压力计算方法，研究了Morison方程的适用范围。对于直径较大的桥墩，为避免Morison方程简化带来的误差，则主要通过辐射波浪理论计算动水压力，在这方面，Li等[7]和Jiang等[8]提出了圆柱形桥墩动水压力的简化计算公式；Wang等[9-12]系统地研究了工程中常用的椭圆形、圆端形、矩形及椭圆形空心桥墩的动水压力简化计算，并提出了相应的动水附加质量简化计算公式；Zhang等[13]结合流固耦合方法对任意形状截面桥墩的动水压力进行了研究。

在桥梁减震方面，黏滞阻尼器作为一种稳定性高、适用性强的减震装置，可有效减小桥梁的地震反应。在阻尼器设计过程中，阻尼器参数优化是关键环节，传统方法主要是通过既定地震波作用下结构响应对阻尼器参数的敏感性分析来进行优化[14-15]。而实际的地震动具有不确定性，采用确定性分析并不能准确反应其随机特性。对此，赵国辉等人采用频域法，对连续梁桥和悬索桥的黏滞阻尼器参数进行了优化[16]。但由于黏滞阻尼器的非线性特性，该方法仅适用于自由度较少的结构。针对上述问题，Symans等[17]提出了基于耗能相等的阻尼器线性化方法，Paola等[18]基于均方差最小提出了随机等价线性化方法，但由于涉及迭代求解，在实际应用过程中随机等价线性化方法应用较少[19]。

本文建立了考虑动水压力作用的2自由度简化分析模型，提出了桥梁黏滞阻尼器参数随机优化的Lyapunov方法。通过Morison方程计算了简化模型的动水压力，根据耗能等效准则对桥中非线性黏滞阻尼器进行了等效线性化，以墩顶位移方差最小为目标，采用提出的随机优化方法进行了桥梁阻尼器参数优化，并研究了动水压力对减震桥梁地震反应的影响和阻尼器的减震性能，对实际跨海桥梁的减震设计具有参考意义。

1 桥梁动水压力计算

对于桥墩直径/波浪波长<0.2的小直径桥墩，结构物的存在对波浪运动无显著影响，可采用Morison方程计算动水压力。对于横向尺寸较小的圆柱体结构，单位长度上动水压力的计算公式为

(1)

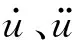
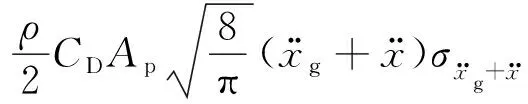
(2)

地震动作用下桥梁结构的运动方程可表示为

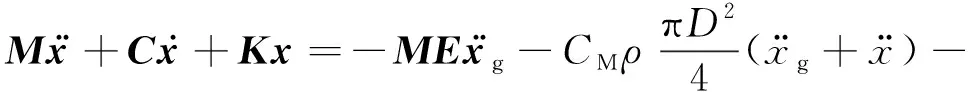
(3)

动水阻力与惯性力相比较小，可忽略不计，式(3)可进一步写为

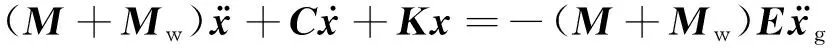
(4)

2 桥梁分析模型

对于规则连续梁桥，可简化成如图1所示的两自由度模型，该模型可很好把握其在地震作用下的动力响应特性[21]。其中，处于完全弹性状态的桥墩，当同时考虑剪切和弯曲变形时，其组合刚度为

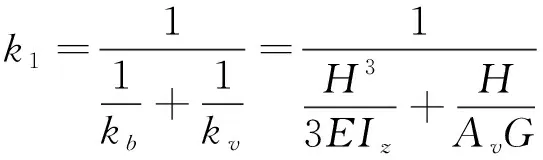
(5)

式中:kb为弯曲刚度;kv为剪切刚度;H为桥墩高度;Iz为桥墩截面惯性矩;Av为桥墩剪切面积;E为弹性模量;G为剪切模量。

(a)(b)图1 减震桥梁模型简化Fig.1 A simplified bridge model with viscous damper

假定桥墩变形形函数为

(6)

形成桥墩的附加质量

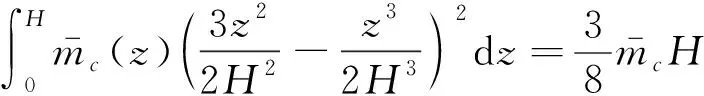
(7)

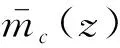
动水压力是以分布荷载的形式作用于桥墩上的，先将桥墩单元上的分布动水压力转化为墩顶的等效结点荷载，为方便使用简化的Morison方程，再将墩顶等效结点荷载转化为墩顶附加动水质量。

3 减震桥梁运动方程

3.1 阻尼力模型

非线性黏滞阻尼器的阻尼力为

(8)

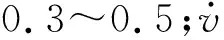
以黏滞阻尼往复一周所耗散的能量与等效阻尼往复一周所耗散能量相等作为线性化的准则，可以得到黏滞阻尼器的等效阻尼系数为

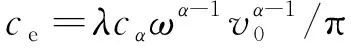
(9)

式中:ce为等效阻尼系数；ω为对应简谐激励的圆频率；v0为阻尼器加载的最大位移；λ为

λ=22+αΓ2(1+α/2)/Γ(2+α)

(10)

式中，Γ(·)为gamma函数。

3.2 运动方程

安装黏滞阻尼器后桥梁在地震作用下的运动方程为

(11)

式中，Ce为设置了黏滞阻尼器的附加阻尼矩阵。

式(11)转化为状态空间形式

(12)

式中：

对本文简化模型

(13)

式中:m1=m*为桥墩墩顶附加质量，m2为桥梁上部结构的集中质量，mw为转化到墩顶的附加动水质量；c1、c2分别为桥墩和支座的阻尼系数；k1、k2分别为桥墩和支座的等效刚度。

4 随机地震响应分析

Clough-Penzien模型为常用随机地震激励模型

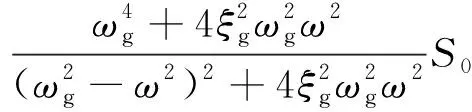
(14)

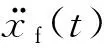
可转化为状态方程

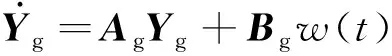
(15)

式中：

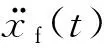
由结构运动状态方程(12)和激励状态方程(15)可得扩展的系统状态方程为

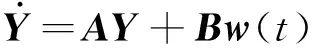
(16)

式中：

令响应的方差矩阵为EY=E(YYT)，Eg=2πBS0BT为输入的协方差矩阵，当输入为稳态时，可得到描述响应方差的Lyapunov方程

AEY+EYAT+Eg=0

(17)

求解上式即可得到结构响应方差。

5 阻尼器参数优化

由阻尼力计算式(8)可知，黏滞阻尼器速度指数α、阻尼系数cα取不同值时对结构响应的影响也不同。在减震设计中需对设置黏滞阻尼器的桥梁进行阻尼器参数α、cα优化，研究参数变化对结构响应的影响规律，为阻尼器设计参数的确定提供依据。

从提高结构安全性能的角度考虑，以墩顶位移方差最小化为优化目标，即：

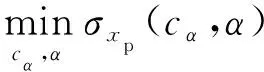
(18)

(19)

约束条件为：s.t.:cα min≤cα≤cα max

αmin≤α≤αmax

式中:Sxx(ω)为墩顶位移响应的自谱密度;cα min、cα max分别为阻尼系数的下限和上限;αmin、αmax分别为阻尼指数的下限和上限。

某一跨海连续梁桥，桥墩为圆柱实体墩，直径3.0 m，墩高28.2 m，水深20 m，上部结构质量取桥墩相邻两个半跨的质量m2=5×105kg，以集中质量的形式作用在支座上，桥墩弹性模量为3.0×104MPa，等效刚度为1.587×107N/m，墩身等效到墩顶的集中质量为186 880 kg，支座等效刚度为7.69×106N/m，结构阻尼比取为0.05，支座阻尼比取为0.10。桥墩直径和水深之比为0.15，根据文献[22]的研究可采用Morison方程计算动水压力。桥梁抗震设防烈度为8度，设计基本地震动加速度为0.2g，场地类别为II类。在随机反应分析时Clough-Penzien谱参数采用文献[23]的方法进行计算。基岩的单边谱密度为S0=13.336 cm2/(rad·s3)，ωg=15.7 rad /s，ξg=0.72，取ξf=ξg，ωf=0.15ωgrad /s。

首先建立了对应本文简化分析模型的梁单元有限元模型，采用峰值为0.1g的El Centro波作为地震动输入，通过对有限元模型动力特性和时程分析的比较来验证本文简化模型的合理性。经计算，本文模型前两阶周期分别为2.01 s、0.61 s，有限元模型前2阶周期为2.03 s、0.66 s，前两阶自振周期接近程度较高。图2给出了两种模型桥面纵向位移反应时程曲线的比较，从中可看出，本文模型和有限元模型桥面位移反应时程曲线吻合程度较好，最大值分别为52 mm和55 mm，误差基本满足5%的要求，说明本文简化分析模型合理有效。

在墩顶与梁体之间设置2套黏滞阻尼器，应用本文提出的方法进行黏滞阻尼器减震优化。图3和图4给出了墩顶位移方差随阻尼系数cα和速度指数α的变化关系。由图3可看出，墩顶位移方差随阻尼系数cα的增大先减小后逐渐增大，对于不同α值的曲线，在cα=1.5×105附近普遍接近最小值。由图4可看出，墩顶位移方差随着速度指数α的增大整体上是减小的，只有cα=1.5×105的曲线在速度指数α=0.45附近取得了最小值。通过综合比较，选择α=0.45、cα=1.5×105为该桥的最优阻尼器参数。

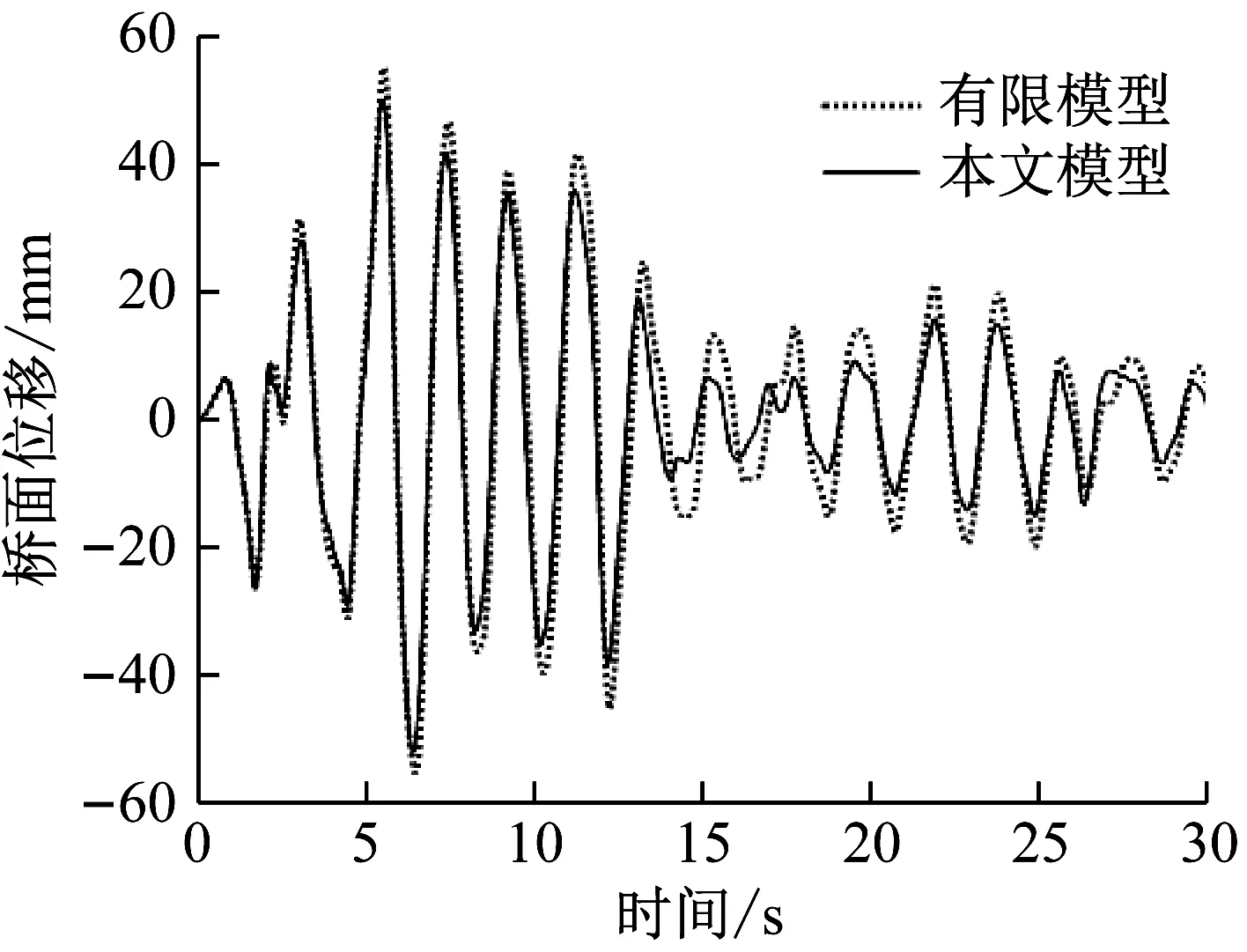
图2 桥面纵向位移时程曲线Fig.2 Longitudinal displacement time history curve

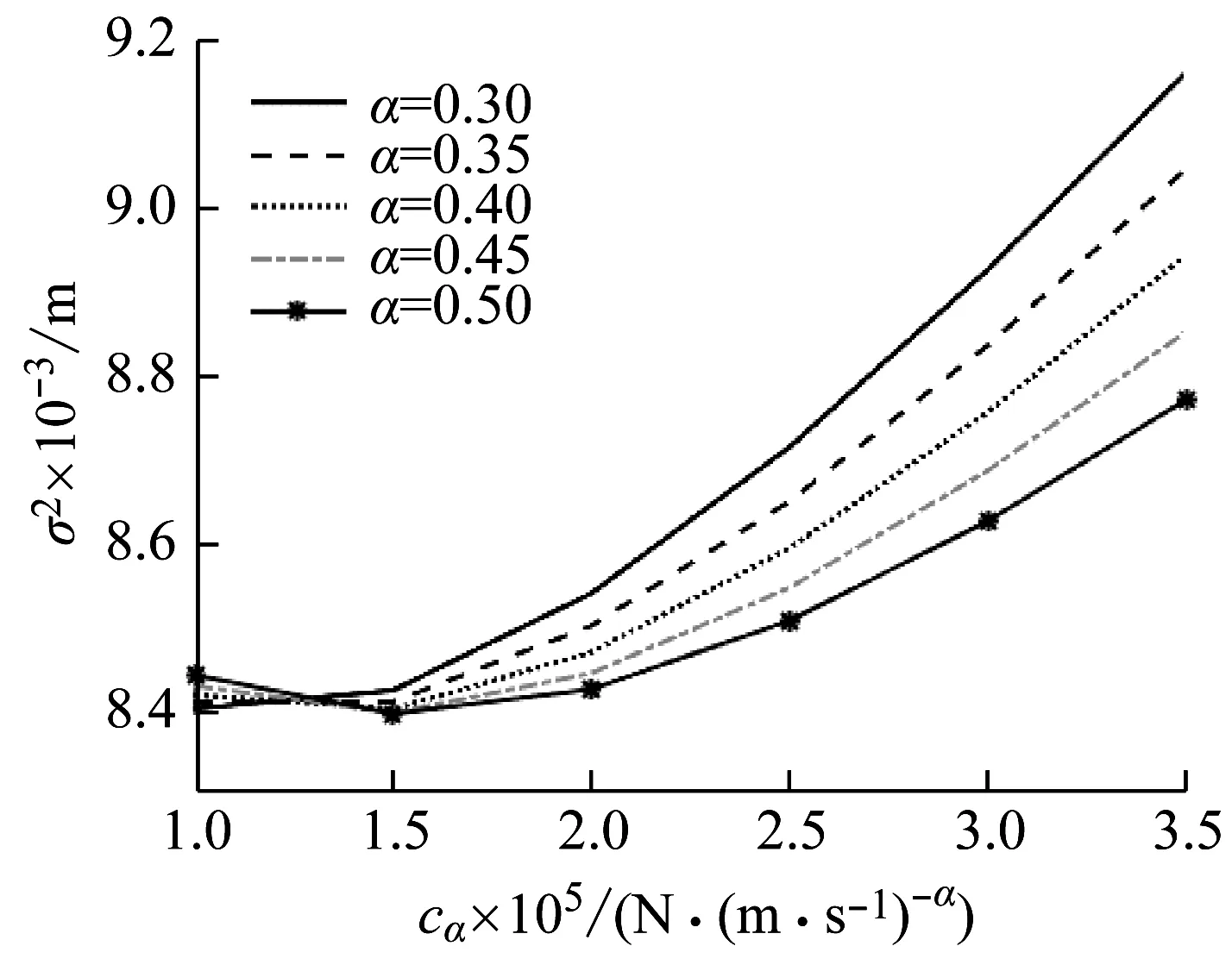
图3 墩顶位移方差随阻尼系数cα的变化Fig.3 Pier top displacement variance versus damping coefficient

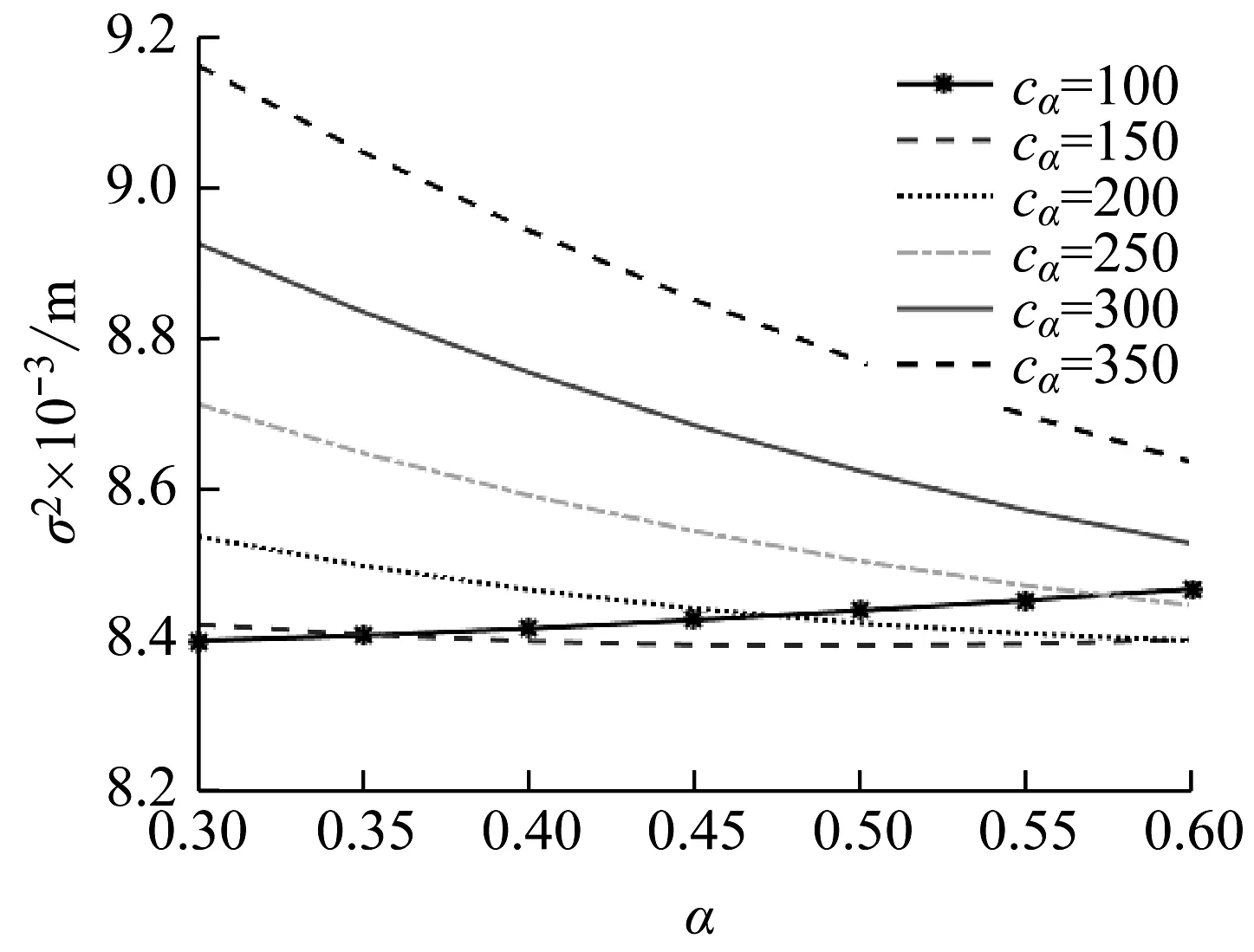
图4 墩顶位移方差随速度指数α的变化Fig.4 Pier top displacement variance versus velocity index

表1列出了α取0.45时cα分别取1.0×105和2.0×105，cα取1.0×105时α分别取0.40和0.50的四组组合和本文优化结果对应的墩顶位移方差。从中可以看出，本文优化结果对应的方差在邻近范围最小，说明本文方法对黏滞阻尼器的优化结果是合理的，也说明了本文方法的有效性。

表1 阻尼器参数对应的墩顶位移方差

6 减震桥梁性能研究

首先进行模态分析，再利用El Centro波和Kobe波进行时程反应分析，分析中结构重要性系数按照文献[24]规定取1.7。表2列出了分别考虑动水压力作用(有水)和不考虑动水压力作用(无水)结构的第一、二阶频率及其变化率。可看出：考虑动水压力作用后，一阶频率降低了0.6 %，二阶频率降低了9.9%，表明水体的存在改变了结构的动力特性。

表2 桥梁自振频率

为分析动水压力对桥梁地震响应的影响，对不设阻尼器时的抗震桥梁，计算了考虑动水压力作用(有水)和不考虑动水压力作用(无水)两种情况下桥梁的地震反应。表3列出了墩顶水平位移、支座位移、墩底弯矩和墩底剪力的地震反应峰值及变化率。图5给出了El Centro波和Kobe波作用下墩顶位移时程曲线。从中可看出：考虑动水压力作用后，El Centro波作用下的墩顶位移、墩底弯矩、墩底剪力普遍增大了10.8%左右，支座位移增大了7.2%；Kobe波作用下的墩顶位移、墩底弯矩、墩底剪力普遍增大了4.7%左右，支座位移增大了7.9%。地震作用下，处在水中的桥墩地震反应受动水压力的影响整体上较为明显，动水压力的存在放大了桥梁的动力响应。因此，对于跨海桥梁，在减震设计中考虑动水压力是必要的。

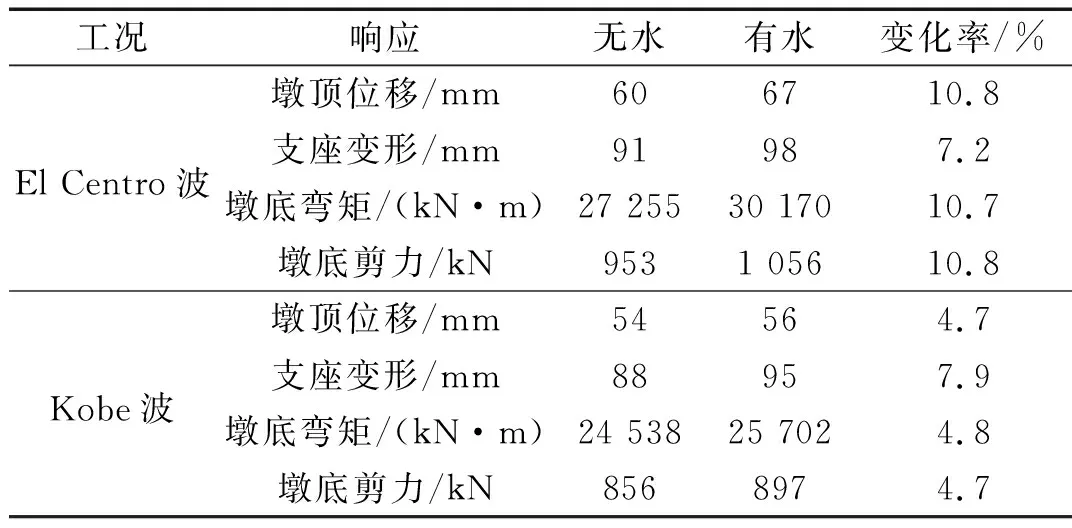
表3 有/无动水压力作用下桥梁地震反应峰值

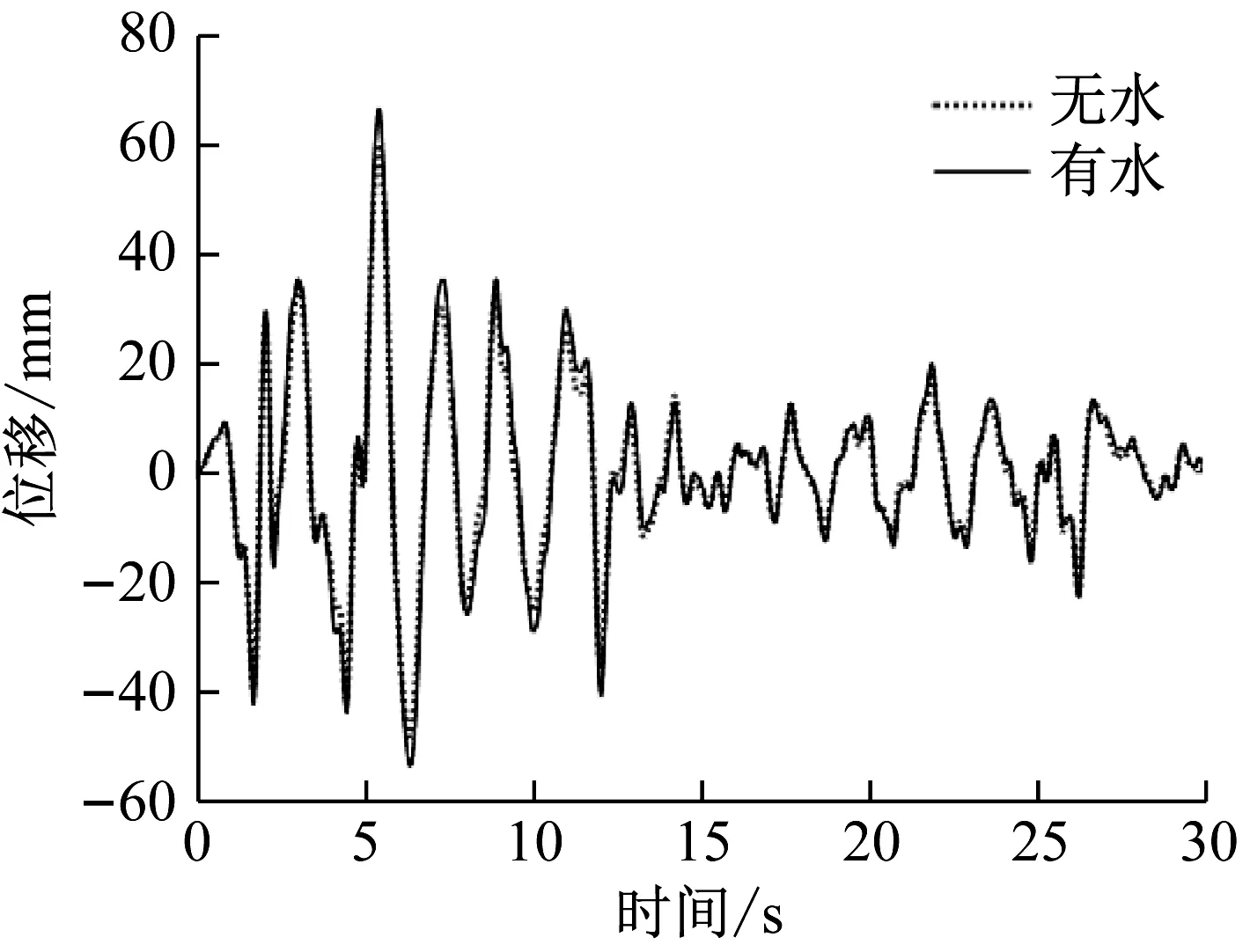
(a) El Centro波

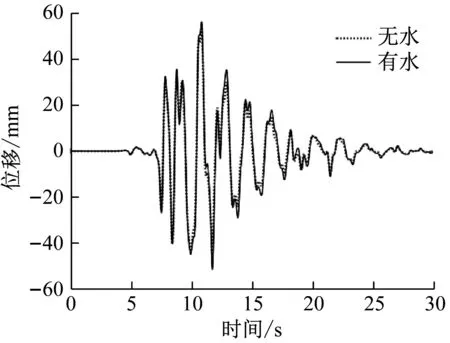
(b) Kobe波图5 有/无动水压力作用下桥梁墩顶位移时程曲线Fig.5 Time history curves of bridge pier top displacementwith/without hydrodynamic pressure

为了衡量控制效果引入了减震率的概念，定义如下

(20)

式中:Ri为第i个自由度的减震率;di,u(t)和di,c(t)分别为抗震和减震情况下结构第i个自由度的地震反应。

表4列出了El Centro波和Kobe波作用下考虑动水压力影响的减震和非减震桥梁的墩顶水平位移、支座位移、墩底弯矩和剪力的峰值及其变化率，图6给出了El Centro波作用下相应的时程曲线。从中可以看出：对于考虑了动水压力的黏滞阻尼器减震桥梁，El Centro波作用下的墩顶位移、墩底弯矩、墩底剪力的减震率在12.3%～14.3%，支座位移的减震率为26.7%；Kobe波作用下的墩顶位移、墩底弯矩、墩底剪力的减震率在8.9%～10.6%，支座位移的减震率为29.5%。本文设计的黏滞阻尼器对桥墩的减震效果比较明显，对支座位移的减震效果尤为明显。采用黏滞阻尼器对跨海桥梁进行减震控制可有效减小结构地震反应，改善桥梁的抗震安全性。

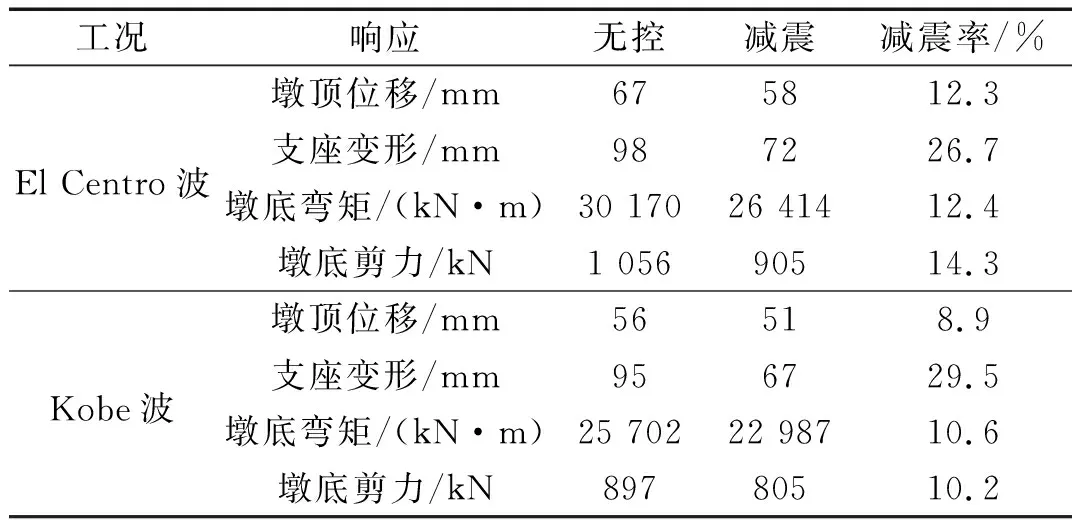
表4 控制效果比较

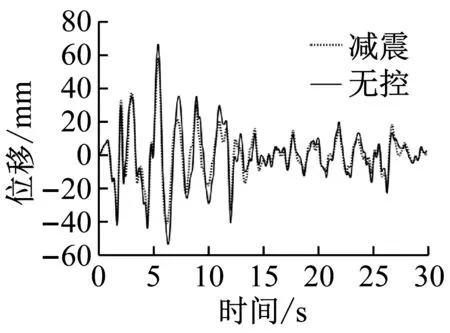
(a) 墩顶位移(b) 支座变形(c) 墩底弯矩(d) 墩底剪力图6 桥梁地震反应时程曲线Fig.6 Seismic response time history curves of bridge

图7给出了El Centro波作用下阻尼器的滞回曲线，可看出在地震作用下黏滞阻尼器滞回曲线饱满、规则、耗能效果明显，考虑动水压力作用的桥梁由于地震反应更大其黏滞阻尼器的耗能效果也更明显。

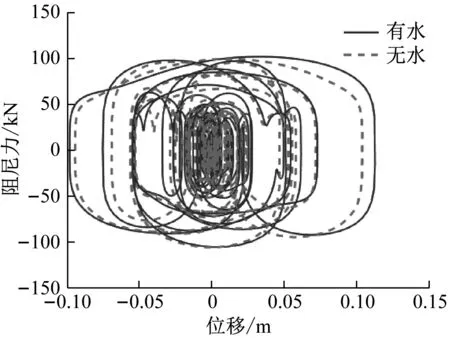
图7 有/无动水压力作用下桥梁黏滞阻尼器滞回曲线Fig.7 Hysteresis curve of viscous damper of bridgewith/without hydrodynamic pressure

7 结 论

本文提出了考虑动水压力作用的桥梁简化分析模型，在此基础上采用随机振动分析的Lyapunov方程进行了黏滞阻尼器参数优化，并研究了动水压力对减震桥梁地震反应的影响和阻尼器的减震性能，得出如下结论：

(1) 本文提出了考虑动水压力作用的桥梁黏滞阻尼器参数随机优化的Lyapunov方程方法，并通过简化的桥梁分析模型验证了方法的有效性。

(2) 本文算例表明考虑动水压力作用后，桥梁的一阶频率降低了0.6 %，二阶频率降低了9.9%，水体的存在改变了桥梁结构的动力特性。

(3) 考虑动水压力作用后，El Centro波作用下的墩顶位移、墩底弯矩、墩底剪力普遍增大了10.8%左右，支座位移增大了7.2%；Kobe波作用下的墩顶位移、墩底弯矩、墩底剪力普遍增大了4.7%左右，支座位移增大了7.9%。地震作用下，处在水中的桥墩其地震反应受动水压力的影响整体上较为明显，动水压力的存在放大了桥梁的动力响应。对于跨海桥梁，在减震设计中考虑动水压力是必要的。

El Centro波作用下的墩顶位移、墩底弯矩、墩底剪力的减震率在12.3%～14.3%之间，支座位移的减震率为26.7%；Kobe波作用下的墩顶位移、墩底弯矩、墩底剪力的减震率在8.9%～10.6%之间，支座位移的减震率为29.5%。

(4) El Centro波作用下桥梁墩顶位移、墩底弯矩、墩底剪力的减震率在12.3%～14.3%之间，支座位移的减震率为26.7%；Kobe波作用下的墩顶位移、墩底弯矩、墩底剪力的减震率在8.9%～10.6%之间，支座位移的减震率为29.5%。地震作用下黏滞阻尼器滞回曲线饱满、规则、耗能效果明显。考虑动水压力作用的桥梁黏滞阻尼器的耗能效果更加明显。阻尼器的设置可有效降低桥梁的地震反应，对支座位移的减震效果尤为明显。

本文的两自由度简化模型对于以剪切变形为主的中、低墩桥梁，结果较为准确，对以弯曲为主的高墩桥梁，由于质量参与和高阶振型的影响，误差较大；由于Lyapunov直接求解方差法仅限于平稳随机模型或等效平稳模型，因此本文方法不能进行完全非平稳随机地震激励下的黏滞阻尼器参数优化。