基于复特征值分析的某盘式制动器制动尖叫问题改进

詹 斌，孙 涛，沈炎武，余家皓，陶 政，胡浩炬

(广州汽车集团股份有限公司汽车工程研究院，广州 511434)

制动器在不断满足和提高产品功能性的同时，出于驾驶和乘坐舒适性的考虑，制动噪声问题日益被消费者所关注。对于汽车制造商，制动噪音问题会增加大量的售后成本并降低客户对汽车质量和可靠性的认可度，因此制动噪声已成为汽车制造商亟待解决的一个重要问题。汽车制动噪音的发生受温度、湿度、制动压力、车速等众多因素的影响，具有很大的随机性，频率覆盖广泛，如频率在1 000 Hz以下的起步咕音(Groan)、咯吱音和Moan音，频率在1 000 Hz以上的制动尖叫(squeal)，且其发生机理复杂，涉及摩擦学、振动力学等众多学科，对其的研究从发生机理到分析方法仍未取得一致结论，也没有形成完善的工程控制手段[1]。

本文针对某车型盘式制动器在低速蠕行工况下出现2 000 Hz制动尖叫问题进行研究，如图1所示，按照SAE J2521规范中的程序,对此制动器在台架上进行噪音搜索试验，在低速低压工况集中复现了2 000 Hz制动尖叫，噪音搜索结果如图2所示。

图1 制动器台架试验Fig.1 Brake bench test

工程上目前在解决制动尖叫类问题时，一般通过摩擦片和消音片的预选以及制动噪音匹配试验的方式来应对，即通过调整摩擦片的开槽、倒角、配方及消音片的阻尼特性，然后在试验台上进行噪音搜索来验证改善效果。有限元复特征值分析方法的提出[2-3]，逐步成为工程上解决或抑制制动尖叫问题的另一有效方法，通过有限元计算提取制动器的复特征值和模态振型，利用特征值的实部或阻尼比来分析系统是否不稳定并判断尖叫发生的倾向[4]。本文即采用有限元复特征值分析方法，结合试验模态及多普勒激光测振手段[5]，基于复特征值及相关性分析的结果调整制动器零件的几何结构，消除了2 000 Hz制动尖叫。

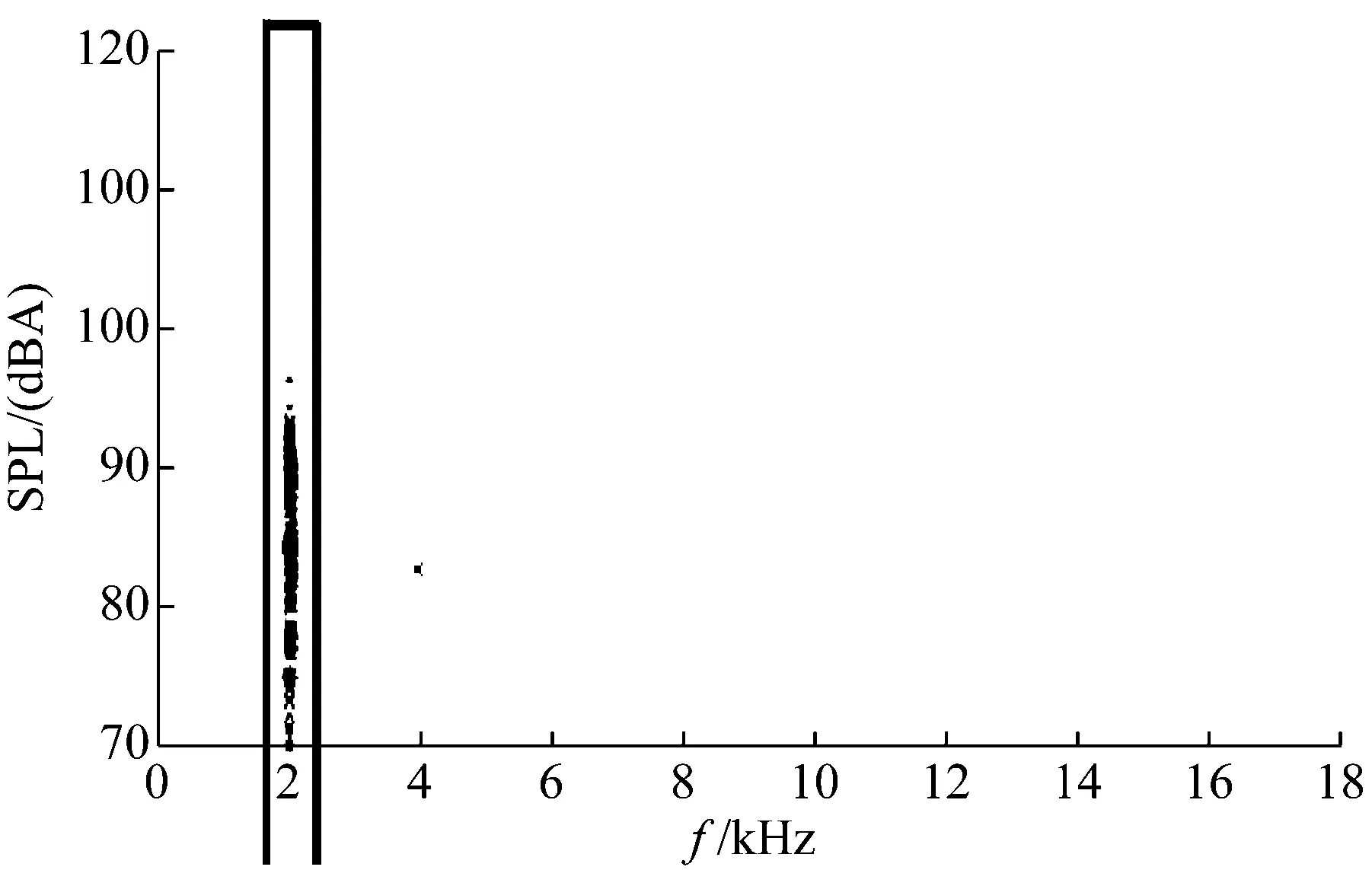
图2 制动器台架噪音搜索试验结果Fig.2 Results of noise in brake bench test

1 复特征值分析理论

复特征值分析基于模态耦合理论，制动盘和摩擦片之间的盘片耦合相当于在系统上提供了一个扰动载荷，它会将导致系统刚度矩阵的不对称，将系统的不稳定模态激励起来。通过对复特征值问题的求解，确定系统中哪些模态是不稳定的，容易发生自激和尖叫[6]。

考虑系统制动时制动盘与摩擦片之间的摩擦力，系统的动力学方程如下

(1)

式中:M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵，u为系统的各自由度的位移向量；Ff为制动盘与摩擦片之间的接触摩擦力，它以接触面之间节点的相对位移来表示为

{Ff}=[Kf]{u}

(2)

这个将摩擦力与节点位移联系起来的矩阵称为摩擦刚度矩阵，或者简称为摩擦矩阵。

结合式(1)和(2),将式(1)中的摩擦力从右边移到左边可写成如下二阶齐次线性微分方程形式

(3)

式(3)是包含了摩擦刚度项的自由振动系统的动力学方程，其解的形式如下

u={Φ}est

(4)

将其进行适当的微分并代入式(3)得到

([M]s2+[C]s+[K-Kf]){Φ}={0}

(5)

式中:Φ为特征向量，s为特征值。不同于系统中惯性力和弹性力导致的对称质量矩阵和刚度矩阵，摩擦力导致的摩擦矩阵Kf是不对称的，它会导致系统的刚度矩阵不对称[7]。刚度矩阵不对称在一定条件下会求解得到如下包括实部和虚部的共轭复特征值

si1,2=σi±jωi

(6)

系统的运动可以用共轭复特征值和特征向量来描述

{ui}={Φi}e(σi+jωi)t+{Φi}e(σi-jωi)t

(7)

通过欧拉公式变换可以得到

{ui}={Φi}eσitcosωit

(8)

对于第i阶模态，σi是其特征值实部，代表系统的阻尼系数，ωi是其虚部，代表系统的阻尼固有频率。正的实部会使振动扩大，发展为强烈的自激振动，此时系统是不稳定的，因而通过对系统特征值实部的分析，可以确认系统中不稳定且容易产生制动尖叫的模态。

2 制动器有限元复特征值分析

2.1 盘式制动器有限元模型

盘式制动器系统有限元模型包括制动盘、卡钳本体、卡钳支架、导向销、内/外制动背板、内/外消音片、活塞、内/外摩擦片以及对手件轮毂轴承、轴节。在Hypermesh中进行几何清理，采用四面体单元划分网格，结合制动器各零件结构和工作原理，采用绑定、接触、刚性连接等方式定义各零件之间的连接关系，装配后形成完整的制动器有限元网格模型如图3所示[8]。

图3 盘式制动器有限元模型Fig.3 FEA model of disc brake

2.2 零部件材料属性定义

定义摩擦片为横观各向同性材料，其属性采用实测值进行设置，摩擦片材料参数如表1所示。

表1 摩擦片材料参数

各零部件通过称重、试验模态进行修正有限元模型中的材料密度和弹性模量，修正后使各零部件的自由模态计算结果与试验模态结果误差在3%以内。以制动盘为例，图4为其模态测试试验。

图4 制动盘模态测试Fig.4 Modal test of brake disc

表2为其修正材料参数后试验与计算模态频率的对比。

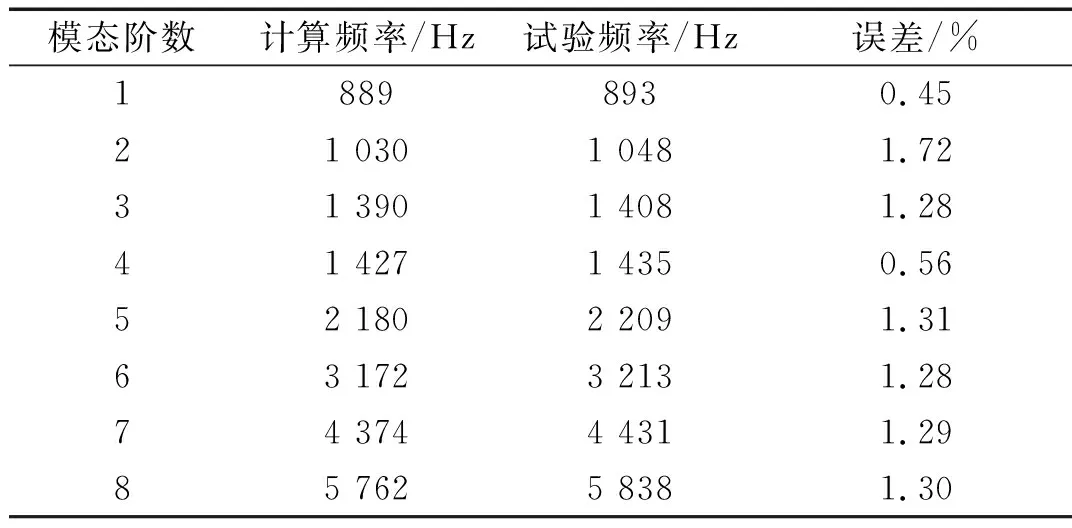
表2 制动盘试验与计算自由模态频率对比

2.3 盘式制动器有限元模型

卡钳支架与转向节之间通过螺栓连接，需对此连接螺栓添加预紧力，转向节和制动盘通过螺栓连接在轮毂轴承的两侧，约束转向节与悬架连接各点的6向自由度，考虑到制动尖叫出现在低速低压工况，一方面需在活塞和卡钳油缸底部施加相应的制动压力，另一方面需对制动盘添加转动效应[9]。制动油压和旋转速度分布如表3，共20个工况进行复特征值的求解。

表3 复特征值分析各工况制动压力

2.4 复特征值分析结果

使用ABAQUS软件提取5 000 Hz以内的盘式制动器复模态结果，如图5，以散点图方式绘制出各工况下出现的不稳定模态的特征值实部和频率的信息。图中的1 900 Hz不稳定模态频率出现的工况次数最多，阻尼系数相对偏高且集中，说明其发生制动尖叫的倾向性较大，同时它与台架噪音搜索结果出现的2 000 Hz的噪声频率非常接近。

图5 盘式制动器复模态分析结果Fig.5 Results of complex eigenvalue analysis

在台架上进行噪音复现的同时，配合三维扫描式多普特激光测振仪，测试系统在2 000 Hz制动尖叫出现时的ODS振型，如图6所示，与复模态仿真分析结果中的1 900 Hz不稳定模态进行对比，确认二者振型是吻合的。因而，可以确认复特征值分析中的1 900 Hz不稳定模态与实际发生噪音模态一致。

(a) ODS测试结果(b) 不稳定模态振型图6 ODS测试与不稳定模态分析结果对比Fig.6 Comparison of ODS test with unstable modal of FEA

各工况出现的不稳定模态中，在650 Hz、2 300 Hz、2 550 Hz频率处也相对比较集中，但实车中并未出现该频率的噪音，这代表仿真结果出现了“过预测”。为了找到与台架上复现的制动尖叫所对应的的不稳定模态，“过预测”现象在本文中是希望出现的。出现“过预测”，原因为对制动盘和摩擦片之间设置了较大的摩擦因数，激励了更多的不稳定模态，且没有考虑摩擦所诱导的阻尼及结构阻尼，阻尼对不稳定模态的出现是有抑制作用的。

3 子零件模态贡献量分析

针对上文已经确认的不稳定模态，通过相关性分析找出与其相关程度较高的实模态，然后统计这些相关程度较高的实模态的应变能信息来量化制动器零件对系统不稳定模态的贡献，据此找到具有最大贡献量的部件，为后续对子零件进行结构优化工作提供依据和指导[10]。

3.1 相关性分析

采用模态置信因子(MAC)来对复模态与实模态进行比较，MAC表示一对向量之间的相关程度，这一对向量可以是复模态向量、实模态向量或者是外界激励工况下的响应向量[11]，通过MAC可以识别出两个在一定摩擦激励下能够发生耦合的实模态。其表达式为

(9)

式中:Ψi、Ψj分别为实模态、复模态各阶模态的振型向量，MACij为第i阶实模态与第j阶复模态之间的相关程度，它的值介于0～1之间，包含了幅值和相位的信息。根据前文所建立的有限元模型，提取系统前5 000 Hz的复模态与实模态各阶模态振型向量，得到系统各阶复模态与实模态的MAC矩阵。针对1 900 Hz(第36阶)的不稳定模态，提取它与各阶实模态的部分MAC值如表4所示，排名前二的第35、36阶实模态与它的相关性为47%、57%，代表了这两阶模态是1 900 Hz不稳定模态的主要参与者。

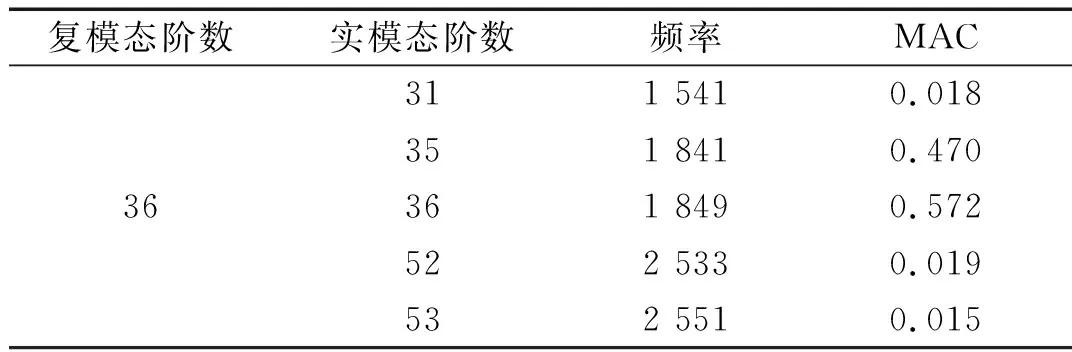
表4 系统复模态与实模态的MAC

3.2 子零件模态贡献量分析

应变能能很好地反映一个子零件对整个系统的贡献，在模态分析中，第i阶模态的第j单元的模态应变能(MSE)定义为

MSEij={Φi}T[Kj]{Φi}

(10)

式中:{Φi}为第i阶模态的振型;[Kj]为j单元刚度矩阵[12]。

针对这两个相关程度最高的实模态，如表5，统计各子零件的应变能信息，结合它们的MAC值进行加权，得到子零件对整个系统不稳态的贡献量，可以看出卡钳支架、卡钳、制动盘主要参与了系统不稳定模态，卡钳支架具有最高的应变能，说明它对系统的贡献是最大的。

表5 子零件应变能

针对卡钳支架，计算其自由模态与系统第35、36阶系统实模态的MAC值如表6所示，可以看出支架的第1、3、4、6阶自由模态最主要的参与了系统的不稳定模态。

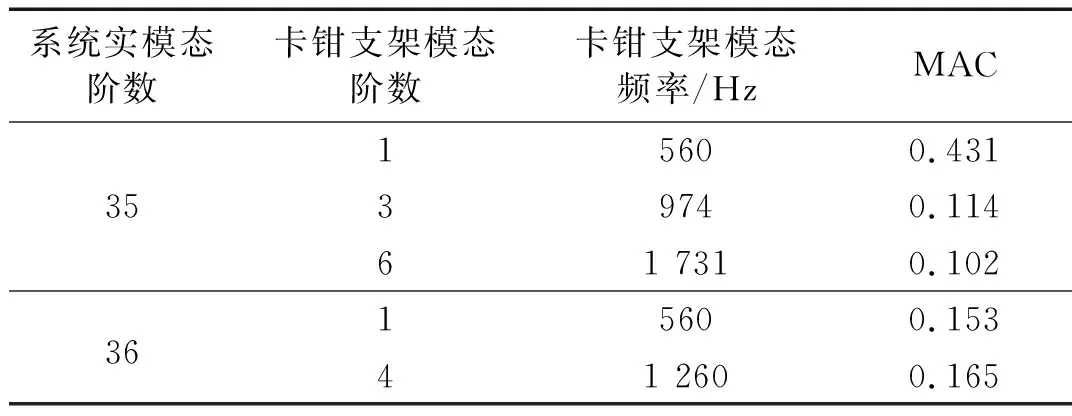
表6 第35、36阶系统实模态与支架的MAC值

支架的不稳定模态及与其相关程度较高的自由模态如图7所示。

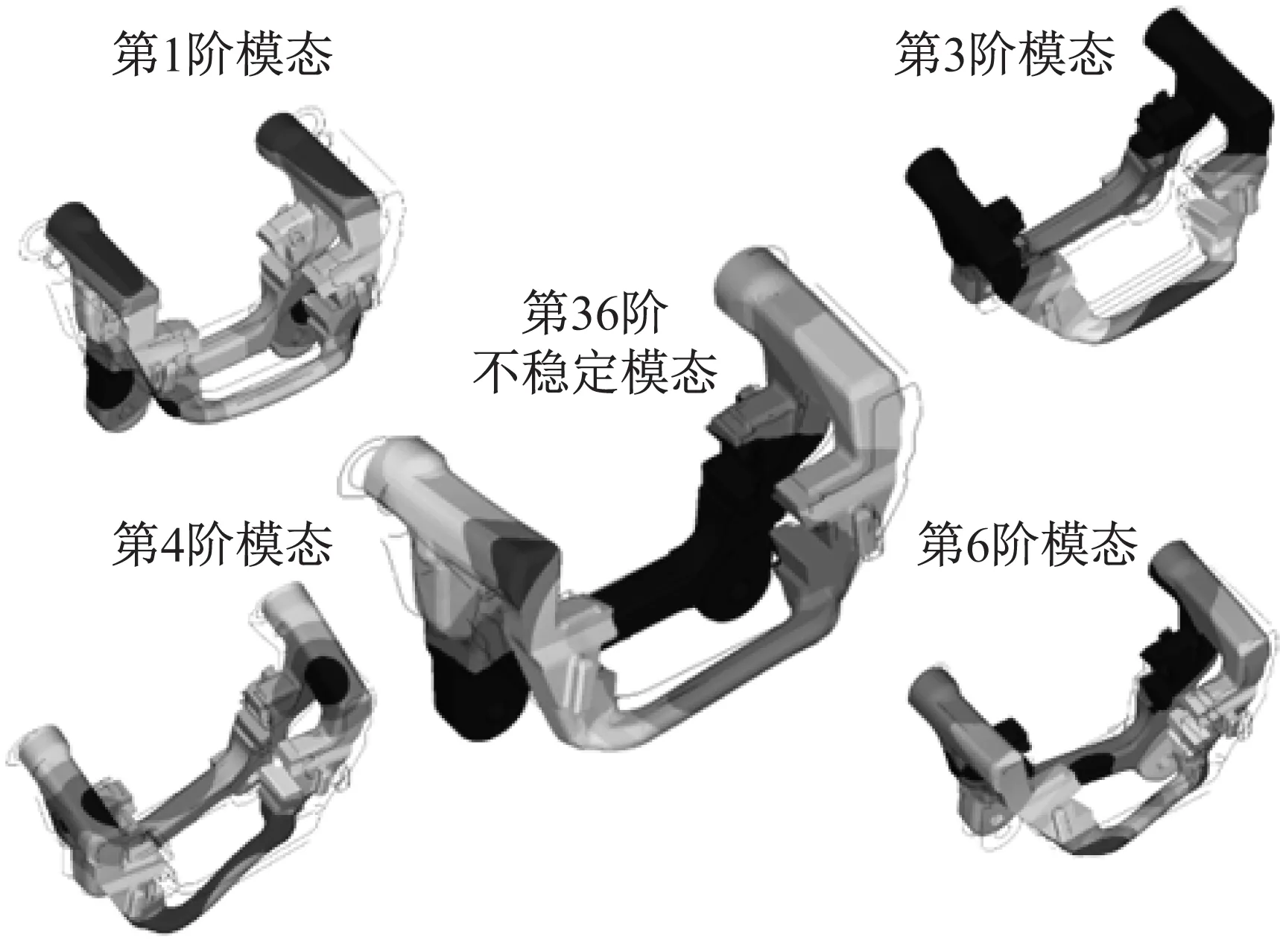
图7 36th不稳定模态中支架振型与其相关程度较高的自由模态振型的对比

4 制动尖叫问题改进

确认了支架的自由模态在系统不稳定模态中贡献量后，可以由图7中观察到支架的第1、3、4、6阶模态振型都表现为支架外端面梁的振动，对比同平台其他车型卡钳支架外端面梁的尺寸，发现此梁相对较细，刚度较弱，如图8所示，本文考虑通过增加支架外端面梁的厚度来提高支架的刚度，期望达到消除系统不稳定性的目的。

图8 卡钳支架的优化方案Fig.8 Modification of caliper bracket

支架修改前后其第1、3、4、6阶自由模态频率变化情况如表7所示。

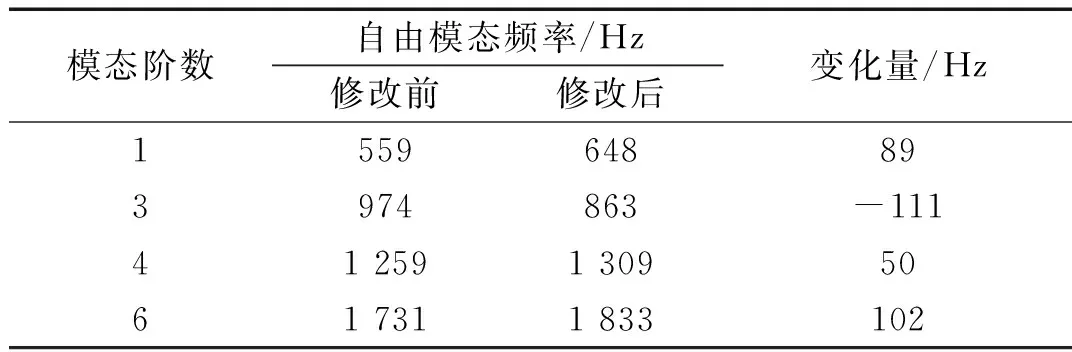
表7 支架修改前后模态频率对比

针对修改支架后的方案进行有限元复模态分析，其仿真结果如图9所示。

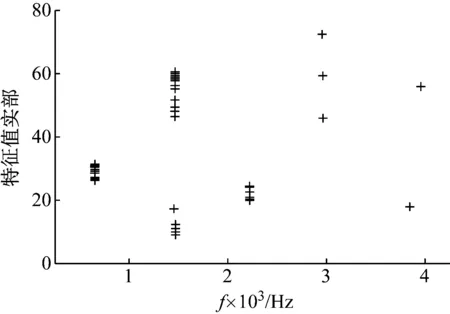
图9 修改支架后盘式制动器复模态分析结果Fig.9 Results of complex eigenvalue analysis after modifying the caliper bracket

从图9的CAE分析结果可以看出，原方案中集中在1 900 Hz的不稳定模态得到了消除，但新出现了1 500 Hz的不稳定模态。对于CAE分析结果中新出现的1 500 Hz的不稳定模态，考虑到以往实车上并未出现过1 500 Hz噪声问题，且其振型已不具有原噪声模态振型的特征，如图10，对新方案在台架上进行噪音搜索，未发现1 500 Hz和2 000 Hz的噪音问题，可以说明1 500 Hz不稳定模态属于“过预测”，修改支架的方案对改进2 000 Hz制动尖叫问题是有效的，因此可以推进此方案实车验证。

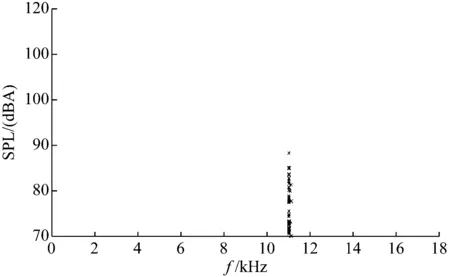
图10 修改支架后制动器台架噪音搜索试验结果Fig.10 Results of noise in brake bench test after modifying bracket

对于台架新出现的11 kHz附近噪音，按照复特征值分析方法，如欲将其消除，应重复以上分析过程，直至得到全面理想的抑噪效果[13]。但考虑到11 kHz噪音分贝值相对较低，且改进过程应充分考虑开发周期及试验成本，同时借鉴前期的开发经验，不同于 1 500～4 000 Hz的中低频制动尖叫应对措施，此11 kHz制动尖叫可通过调整消音片的阻尼特性及摩擦片的开槽倒角来快速匹配抑制，对这一噪音匹配过程，本文不作进一步论述。

5 结 论

(1) 利用有限元法建模及复特征值分析方法提取系统的不稳定模态，通过与出现制动尖叫时的ODS测试结果进行对比，确认对应的不稳定模态。

(2) 通过相关性分析找出与不稳定模态相关程度较高的实模态，然后统计这些相关程度较高的实模态的应变能信息来量化制动器子零件对系统不稳定模态的贡献，据此找到具有最大贡献量的部件。

(3) 通过优化具有最大贡献量的子零件结构，改变其模态，消除了对应2 000 Hz制动尖叫的系统不稳定模态，且台架验证未出现2 000 Hz噪音，说明了复特征值分析方法对于改善制动尖叫的可行性和有效性。