初始几何缺陷模式对单层球面网壳抗震性能的影响
张 明,侯积英 ,支旭东,李文亮
(1.东南大学 混凝土与预应力混凝土结构教育部重点实验室,南京 210018;2.西南交通大学 土木工程学院,成都 610031; 3.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室,哈尔滨 150090;4.哈尔滨工业大学 土木工程智能防灾减灾工信部重点实验室,哈尔滨 150090)
单层网壳结构属于初始几何缺陷敏感性结构,特别是大跨度和超大跨度单层网壳,初始几何缺陷能够较大幅度地降低其稳定性或其极限承载能力[1]。但是鉴于制作与拼装,实际工程中的单层网壳结构体系不可避免地存在初始几何缺陷。因此,在设计和分析过程中必须考虑初始几何缺陷对单层网壳工作性能的影响。研究发现,网壳的初始几何缺陷主要包括安装偏差、节点位置偏差、杆件缺陷-初弯曲和初偏心等[2]。对于初始几何缺陷的幅值,《空间网格结构技术规程》[3]在基于大量的算例研究,规定了“按网壳跨度的1/300”作为理论计算的取值;至于杆件的初始几何缺陷,《空间网格结构技术规程》规定在单层网壳结构设计中需限制杆件长细比而得到控制;而对于节点安装偏差分布模式,《空间网格结构技术规程》认为初始几何缺陷按最低阶屈曲模态分布时,对网壳稳定性承载力的影响是最不利的,因此其推荐采用最低阶屈曲模态来考虑节点安装偏差分布。在上述规定基础上,众多学者对单层网壳的初始几何缺陷施加方案进行了改进和完善,如部分学者经探索性研究之后认为基于结构最低阶屈曲模态来表征单层网壳的节点安装偏差分布模式比较合理[4-8];也有部分学者提出不同的初始几何缺陷施加方法,如第一阶非对称屈曲模态法[9]、以弯曲应力为主杆件数量占有效杆件总数的百分比最大为判断准则施加最不利初始几何缺陷法、局部几何缺陷法[10]、随机缺陷模态法[11-13]、模态叠加法、N阶特征缺陷模态法[14]。上述初始几何缺陷-节点安装偏差分布的探索多针对结构静力稳定性能,鲜有开展地震动作用下初始几何缺陷分布模式对单层网壳结构受力状态及失效影响的研究。
本文以唐山地区某假想百米跨度单层球面网壳以及其它不同跨度和矢高的单层球面网壳为例,研究四种不同初始几何缺陷模式对单层球面网壳动力工作性能和承载能力的影响,从而探索地震作用下单层球面网壳的最不利初始几何分布模式。
1 四种初始几何缺陷模式简介
目前施加初始几何缺陷的常用方法有一致缺陷模态法、特征值缺陷法和一阶振型缺陷法。由于随机模态有无限多种、计算量巨大,因此本文并未对单层网壳施加该类型初始几何缺陷模式。
1.1 一致缺陷模态法[15]
屈曲模态是结构屈曲临界点处的位移增量模式,最低阶屈曲临界点所对应的位移增量模式为结构的最低阶屈曲模态。用归一化的最低阶屈曲模态乘以某一幅值系数来模拟结构的初始几何缺陷分布模式,被称为一致缺陷模态法[15]。根据文献[16],一致缺陷模态又分为一致缺陷模态一和一致缺陷模态二。利用“弧长法”、对理想单层网壳开展一次完整的静力非线性全过程分析,之后对屈曲前、后两个邻近状态的位移形态做差值,最终获得的节点位移模式称为一致缺陷模态一。
对于一致缺陷模态一,可以通过特征方程(1)求解得到
[Ke(δ)+Kg(δ)]δ=μQ
(1)
式中:Ke(δ)为考虑材料非线性后、与位移域δ相应的切线刚度矩阵;Kg(δ)为与位移域δ相应的几何刚度矩阵;Q为外荷载;μ为与Q相应的荷载乘子。
基于式(1)求得荷载-位移曲线峰值时刻后一荷载步和峰值时刻前一荷载步对应的节点位移。这里,峰值时刻前一荷载步对应的节点位移向量的模记为Up-1,i,峰值时刻后一荷载步对应的节点位移向量的模记为Up+1,i,p代表峰值时刻的荷载频数,i代表节点编号。取峰值时刻后一荷载步和峰值时刻前一荷载步对应的位移差,记为
ΔUi=Up+1,i-Up-1,i
(2)
则根据一致缺陷模态一方法,施加给理想网壳结构的初始几何缺陷模式可以用ΔU表示
ΔU=R·ΔUi/|ΔUi|max
(3)
式中,R为缺陷值大小,本文取L/300。
在此基础上,获得修正后的单层网壳节点坐标Ux,Uy和Uz为
Ux=U0x+ΔUx
Uy=U0y+ΔUy
Uz=U0z+ΔUz
(4)
式中:U0x,U0y和U0z分别为理想单层网壳的节点三向坐标;ΔUx,ΔUy和ΔUz分别为基于式(3)获得的节点三向位移差值。
通过式(1)~(4)即可实现初始几何缺陷——一致缺陷模态一的施加。
在有限元计算方法中,改换“弧长法”为“牛顿拉普森法”,同样基于式(1),获得峰值时刻处对应的节点位移向量的模(记为Up,i)及峰值时刻前一荷载步对应的节点移向量的模(记为Up-1,i),而后基于下式求解出ΔUi
ΔUi=Up,i-Up-1,i
(5)
在式(5)的基础上,采用式(3)和式(4)便可实现一致缺陷模态二的施加。
1.2 特征值缺陷法
基于屈曲分析特征方程(式(6)所示)针对理想单层网壳结构的初始刚度矩阵,利用“分块兰索斯(LANB)”求得屈曲分析特征方程中最低阶特征值所对应的屈曲模态,然后将归一化的屈曲模态乘以某一幅值系数后、施加给理想网壳的节点坐标,该方法称为特征值缺陷法。
[Ke+λiKg(σ)]Φi=0
(6)
在特征值缺陷计算过程中,根据特征方程(6)采用“分块兰索斯(LANB)”法求解最低阶屈曲模态。但是式(6)中的Ke为不考虑材料非线性的弹性矩阵,Kg(σ)根据下式计算获得
[Ke+Kg(σ0)]δ=Q
(7)
式中,Kg(σ0)为与初始应力σ0相关的几何刚度矩阵。
获得单层网壳最低阶屈曲模态ΔUi后,借用式(3)和式(4)即可将特征值缺陷模态施加于理想单层网壳。另外,该缺陷模式仅考虑了节点安装偏差,未计入杆件弯曲。
1.3 一阶振型缺陷法
基于多自由度自由振动特征方程(式(8)所示),借用模态分析中的“分块兰索斯(LANB)”方法求解理想单层网壳第一阶自振频所对应的振型Φ1,然后将归一化的一阶振型乘以某一幅值系数R后、获得ΔU,而后根据式(4)修正理想网壳的节点坐标,该方法称为一阶振型缺陷法。
(8)
式中,ωn为结构自振圆频率。
理想单层球面网壳模型和施加四种缺陷后的单层球面网壳模型如图1所示,其所对应的结构自振频率如表1所示(屋面的设计荷载转化为了节点质量)。
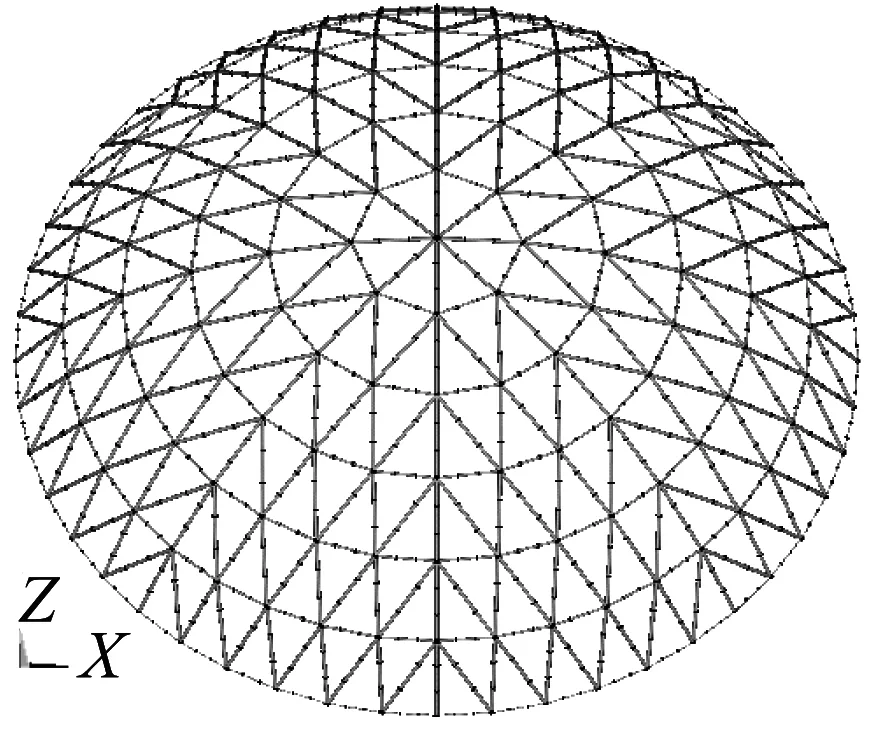
(a) 理想网壳(无缺陷)

(b) 一致缺陷模态一(c) 一致缺陷模态二

(d) 特征值缺陷(e) 一阶振型缺陷图1 网壳的四种初始几何缺陷Fig.1 Four initial geometric imperfections

表1 不同缺陷模式下网壳结构前10阶自振频率
从图1中可见,一致缺陷模态一和模态二均在顶点及第一环向上凸起,第二环处略有下凹,结构其它部位无明显变形,结构局部变形较为明显;特征值缺陷模式在模型中部环带有凹陷,节点偏差较多;一阶振型缺陷模式整体变形较大,偏差节点数量较多,但是弯曲杆件数量不是特别多,说明结构整体刚度削弱不是特别大。从表1中可见,施加四种缺陷模式后网壳的自振频率与理想网壳的自振频率均较为接近。相对而言,一致缺陷模态二所对应的自振频率与理想网壳的频率相差较大。
2 单层球面网壳有限元模型及地震波的选取
基于ANSYS有限元程序参数化设计语言编制不同类型的K8型单层球面网壳(如图2和3所示)研究不同类型初始几何缺陷对结构动力工作性能及承载能力的影响。网壳支座假定为与基础固接;杆件采用管单元(PIPE20,如图4所示),计算中考虑管单元的塑性和大挠度;杆件材料为Q235,材料本构关系如图5所示,屈服强度为235 MPa;动力计算过程中,结构阻尼采用经典阻尼-瑞利(Rayleigh)阻尼(阻尼比取0.02),同时考虑几何非线性和材料非线性;分别对不同类型单层网壳施加上述四种初始几何缺陷,最大缺陷幅值均取跨度的1/300。

图2 单层球面网壳结构示意图[17]Fig.2 Single-layer reticulated dome of Kiewit system

图3 单层球面网壳编号及说明Fig.3 The serial number and declaration of the dome

图4 管单元 PIPE20[17]Fig.4 The PIPE20 geometry

图5 材料本构关系Fig.5 Constitutive model of Q235
本研究采用发生于1976年7月28日的唐山地震主震实测三向地震动记录七条,编号分别为TS01-001、TS01-014、TS01-022、TS01-035、TS01-036、TS01-039、TS01-043。地震动三个方向峰值比值被调整为1∶0.85∶0.65,采样时间间隔为0.01 s。以TS01-001为例,其调整后的地震动记录如图6所示。

图6 TS01-001地震动Fig.6 The seismic wave of TS01-001
3 动力响应分析-算例分析
3.1 100 m跨度单层球面网壳在不同地震动作用下
本单层球面网壳假定为唐山市路南区某大型展览馆屋盖(如图2所示),跨度100 m、矢高30 m、节点与杆件之间为刚性连接、网壳周边与支座为刚性连接。屋面恒荷载为0.5 kN/m2,屋面均布活荷载为0.5 kN/m2,考虑半跨均布雪荷载(取100年重现期基本雪压,0.4 kN/m2),考虑风荷载(取100年重现期基本风压,0.45 kN/m2)。钢管截面根据当地场地条件所对应的最不利荷载组合及规范[3]中对于杆件长细比控制要求进行静力设计,并进行截面选择:主肋Φ480 mm×9 mm、1~3环环杆Φ325 mm×9 mm、4环和5环环杆Φ325 mm×7.5 mm、6环环杆Φ159 mm×5 mm、2~6环斜向杆件Φ480 mm×9 mm。鉴于网壳结构的重要性,取8度区罕遇地震动峰值(取510 mm/s2)对网壳结构的动力响应进行分析。其中,变形云图所图7所示,节点位移放大200倍;应力云图如图8所示;为定量体现结构整体受力特征,给出了结构整体变形能随地震动持续时间的关系,如图9所示。

(a) 一致缺陷模态一(b) 一致缺陷模态二

(c) 特征值缺陷(d) 一阶振型缺陷图7 地震波TS01-001作用下网壳变形云图(位移放大200倍)Fig.7 Deformation of the dome subjected to record TS01-001
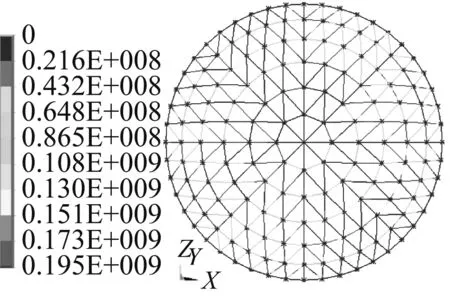
(a) 一致缺陷模态一(b) 一致缺陷模态二

(c) 特征值缺陷(d) 一阶振型缺陷图8 地震波TS01-001作用下网壳应力云图

(a) 一致缺陷模态一(b) 一致缺陷模态二

(c) 特征值缺陷(d) 一阶振型缺陷图9 地震波TS01-001作用下网壳总变形能
从图7可以看出,施加地震动TS01-001(8度区、罕遇地震)作用,考虑一致缺陷模式模态一、模态二和考虑特征值缺陷模式时,单层网壳呈现整体变形,最大节点位移分别为6.51 cm、6.52 cm和6.30 cm;考虑一阶振型缺陷时,单层网壳仍然呈现整体变形趋势,但最大节点位移有增加,约为7.87 cm。所施加四种缺陷模式的网壳在该条地震动作用下产生的最大节点位移均小于《空间网格结构技术规程》中3.5.1条中规定的单层网壳结构容许挠度值(1/400的跨度,250 mm)。从图8中可以看出,考虑一致缺陷和一阶振型缺陷模式时,应力较大的杆件主要集中网壳模型的中部,且施加一阶振型缺陷的网壳中部分杆件的应力达到屈服强度(235 MPa);考虑特征值缺陷模式时,应力较大杆件单元主要集中网壳中上部环杆处。从图9中可以看出,考虑一致缺陷模式模态一、一致缺陷模式模态二、特征值缺陷模式和一阶振型缺陷模式后,网壳结构在该条地震动作用下产生的最大整体变形能分别约为2.5×105J、2.5×105J、2.4×105J、3×105J。
通过上述分析,可以发现,四种缺陷分布模式下网壳的动力响应较为接近。考虑一阶振型模式分布时,网壳在该地震动作用下的最大节点位移、单元应力和结构整体变形能相对较大,且有部分杆单元的应力值接近了材料屈服强度。进一步,对考虑上述四种缺陷模式的网壳分别开展全荷载域动力时程分析,获得其动力失效荷载,如表1所示。

表1 地震动TS01-001作用下单层网壳的失效荷载
从表1中可以看出,施加一致缺陷模态一和一阶振型缺陷后,单层网壳的动力失效荷载相对较小。考虑到地震动的不确定性,对上述网壳分别施加表1中四种初始几何缺陷后、再分别输入峰值为510 mm/s2的所选择的唐山地震主震实测三向地震动其它六条记录,将计算所得网壳最大节位移值列于表2中。

表2 单层网壳在不同地震动作用下最大节点位移值
从表2中可见:①基本设防烈度8度区罕遇地震动作用下,所施加四种缺陷模式的网壳产生的最大节点位移均小于250 mm(单层网壳跨度的1/400),能够满足规范对于结构“大震不倒”的规定;②每种缺陷模式下不同地震动所对应的最大节点位移都具有一定的差异,表明地震动效应具有不确定性;③四种缺陷模式下,网壳结构节点动力位移比较接近。相对而言,施加一阶振型初始几何缺陷后,网壳最大节点位移值较大;④TS01-022地震动作用下,网壳最大节点位移值最大,其原因可能为该条地震波的卓越频率与该网壳的共振区比较接近或者重合。
3.2 不同跨度和矢高的单层球面网壳
在上述分析基础上,分别对跨度为40 m、60 m和80 m的单层球面网壳(屋面均布荷载分别取值为60 kg、200 kg、100 kg)分别施加上述四种初始几何缺陷模式,输入地震动TS01-001(加速度峰值同样取510 mm/s2),开展动力时程分析,获得施加四种初始几何缺陷模式后的不同单层网壳的最大节点位移,列于表3中。

表3 地震动TS01-001作用下不同单层网壳的最大节点位移
从表3中可见:①基本设防烈度8度区罕遇地震动作用下,所施加四种缺陷模式的网壳产生的最大节点位移均小于《空间网格结构技术规程》中3.5.1条中规定的单层网壳结构容许挠度值(单层网壳跨度的1/400),能够满足规范对于结构“大震不倒”的规定;②除网壳D40063外,对于矢跨比为1/3的单层网壳,施加一致缺陷模态一后网壳的最大节点位移值均较大;其它网壳,除D80107外,施加了特征值初始几何缺陷模式后网壳的最大节点位移值均较大。对于精细化分析模型,建议分别考虑施加四种初始几何缺陷模式后开展相关动力分析,而后取动力响应较大的缺陷模式作为该球面网壳的初始几何缺陷模式。
4 结 论
本文初步探索了四种初始几何缺陷模式(一致缺陷模态一、一致缺陷模态二、特征值缺陷和一阶振型缺陷)对单层球面网壳动力性能的影响。结论如下:
(1) 多数工况下,施加四种初始几何缺陷模式后的动力响应较为接近;
(2) 对于矢跨比为1/3的单层网壳,一致缺陷模态一对网壳的抗震性能较为不利;其它矢跨比工况下,特征值初始几何缺陷模式对网壳的抗震性能较为不利;
(3) 本文仅对单层球面网壳施加了四种初始几何缺陷模式开展了动力抗震性能研究,上述四种缺陷模式对于其它类型单层网壳的动力性能影响还需要在以后的研究中继续探索。
致谢
感谢中国地震局工程力学研究所“国家强震动台网中心”为本研究提供唐山地震强地震动记录支持。

