焊接环式箍筋约束高强混凝土柱抗震性能研究

白巨巨，李升才，朱永浦

(华侨大学 土木工程学院,福建 厦门 361021)

新型RCS组合结构由焊接环式箍筋约束高强混凝土柱、焊接六边形孔蜂窝钢梁和普通混凝土(含压型钢板)合成楼盖组成的组合框架结构。该RCS组合结构具有良好的抗震性能。首先，在高强RC柱中配置复合焊接环式箍筋，箍筋对混凝土具有较强的约束作用，能有效地提高构件的抗剪承载力和延性，并改善节点脆性破坏的性质，综合地提高结构的抗震性能。此外，通过控制钢梁的强度使梁端产生塑性铰，使得钢梁可以充分的耗散地震能量，并且采用与普通钢梁相比性能不明显下降的焊接六边形蜂窝钢梁，又进一步减少钢材用量、减轻结构自重。为推动此RCS组合结构的大规模应用，有必要对其主要受力构件即复合焊接环式箍筋约束高强混凝土柱进行抗震性能研究。李升才[1]在高轴压比下对焊接环式BCCS高强混凝土柱进行拟静力试验，研究参数主要是轴压比、配箍率、箍筋形式，研究该类构件的破坏过程、破坏形态、滞回曲线、延性性能、耗能性能,分析塑性铰区域剪切变形角。研究结果表明所有试件最终破坏均呈倒三角形的弯曲型破坏形态，且在较低轴压比和高配箍率条件下，此结构的各项抗震性能指标明显提升。苏俊省等[2]对不同箍筋强度的螺旋箍筋约束混凝土圆柱进行抗震性能试验，主要分析箍筋强度对试件破坏状态、滞回曲线、骨架曲线、抗弯承载力、变形能力、延性性能和耗能能力的影响。结果表明在低轴压比下试件采用高强度箍筋等强度代换普通箍筋时，试件承载力、变形能力、延性性能和耗能能力等抗震性能基本保持不变；但采用高强度箍筋可以减少钢筋用量。Eom等[3]进行了连续矩形或多边形螺旋箍约束混凝土柱的拟静力试验研究，分析了连续螺旋箍的形状、间距和直径对其抗震承载力的影响，试验证实了连续螺旋箍可以有效提高构件承载力、延性和耗能能力，而且提出了限制塑性铰区域纵向钢筋屈曲对螺旋箍竖向间距的要求。但目前研究普遍存在试件过少，参数变化范围较小等缺点，且对于轴压比、配箍率等关键参数对焊接环式RC柱抗剪承载力的研究大都进行定性分析，很难应用于工程实际，本文通过试验与有限元结合方式，一方面对试验结果进行验证，一方面扩大参数分析，在保证结论的准确性同时，针对轴压比，配箍率对柱的水平承载力的影响进行深入系统研究，建立起相应的数学模型，为设计人员提供参考。

1 试验介绍

1.1 试件设计

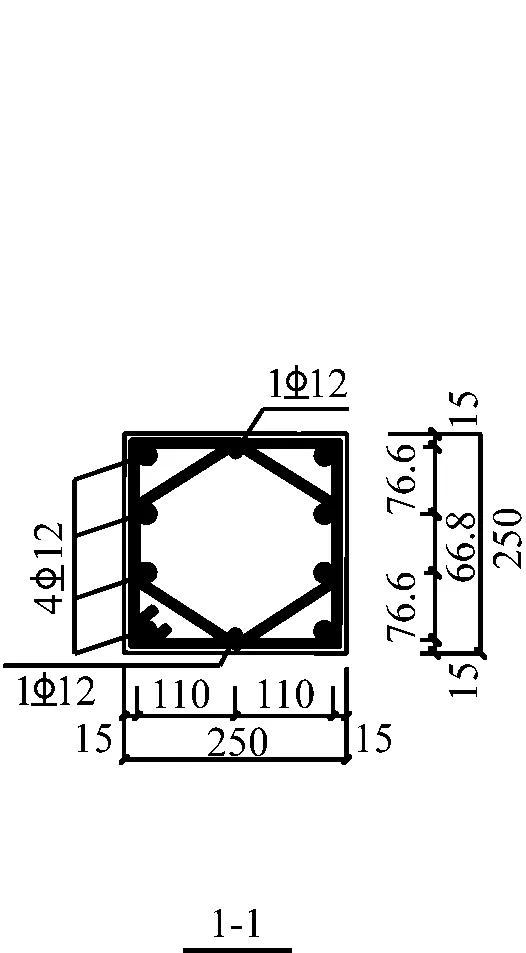
图1 试件尺寸与配筋构造Fig.1 Specimen size and reinforcement construction

1.2 试件加载制度

试验采用加载装置如图3。液压千斤顶主要是施加竖向力，其与柱子通过球铰相连，球铰可左右自由转动；水平力由MTS电液伺服加载系统进行控制，通过此系统施加水平位移来控制力的大小，加载制度见表3。

图2 焊接环式箍筋搭接焊形式Fig.2 Overlap welding form of welded ring stirrups

表1 试验各试件参数

表2 钢筋材料性能

图3 加载装置示意图Fig.3 Schematic diagram of loading device

试件在弹性阶段时，每级加载循坏一次，当试件进入屈服阶段后，每级循环变为三次。

2 有限元模型建立

2.1 材料本构关系选取

2.1.1 混凝土损伤塑性模型

ABAQUS软件中提供三种混凝土本构模型，分别为弥散裂缝模型(只适用于ABAQUS/standard中)、脆性破裂模型、塑性损伤模型。其中塑性损伤模型适用于混凝土的各种荷载分析、单调应变、循环荷载、动力荷载包含拉伸开裂和压缩破碎，此模型可以模拟硬度退化机制以及反向加载刚度恢复的混凝土力学特性。针对本次试验特点，混凝土本构关系选取混凝土塑性损伤模型。

表3 加载制度

2.1.2 混凝土单轴受压应力-应变曲线的选择

本文选取GB 50010—2002《混凝土结构设计规范》[4]所给出的混凝土单轴受压应力-应变曲线为基础，对混凝土本构关系进行试算。受压部分部分表达式为

(1)

式中：aa、ad为单轴受压应力应变曲线上升段、下降段的参数值，取值见文献[4];fc为混凝土的轴心抗压强度标准值;εc为混凝土轴心受压应变标准值;σ为混凝土受压应力;ε为混凝土受压应变。

受拉部分应力-应变曲线

(2)

式中：at为单轴受拉下降段参数值;at取值见文献[4];ft为混凝土的轴心抗拉强度标准值，εt为混凝土轴心受拉应变标准值，σ1为混凝土受拉应力，ε1为混凝土受拉应变。

2.1.3 钢筋本构模型

钢筋的本构采用理想双折线模型，即屈服前为完全弹性的，屈服后的应力—应变关系化为平缓的斜直线，斜率取Ep=0.01Es，数学表达式为[5]

(3)

式中：Es、Ep、fy别代表钢筋的屈服前弹性模量、屈服后的弹性模量和钢筋的屈服强度;σs为钢筋受拉应力;εs为钢筋受拉应变;εy为钢筋屈服应变。

在此种双线型模型中，反向加载刚度和初始刚度相同，不能反映混凝土反向加载时损伤积累的影响，这与实际钢筋混凝土的弯矩——曲率关系有较大差别，为此，引入Clough本构模型[6]子程序(如图4)，在模型中，反向加载曲线指向历史最大变形点(A点)，若该方向没有屈服则指向屈服点(B点)。

2.2 试件尺寸与模型建立

以试验的试件为基础建立有限元模型如图5，其中箍筋直径均为10 mm,纵筋直径20 mm，构造纵筋直径12 mm。结合试验测量结果并参考文献[6]，选定混凝土与箍筋的性能参数。

图4 Clough本构模型Fig.4 Clough constitutive model

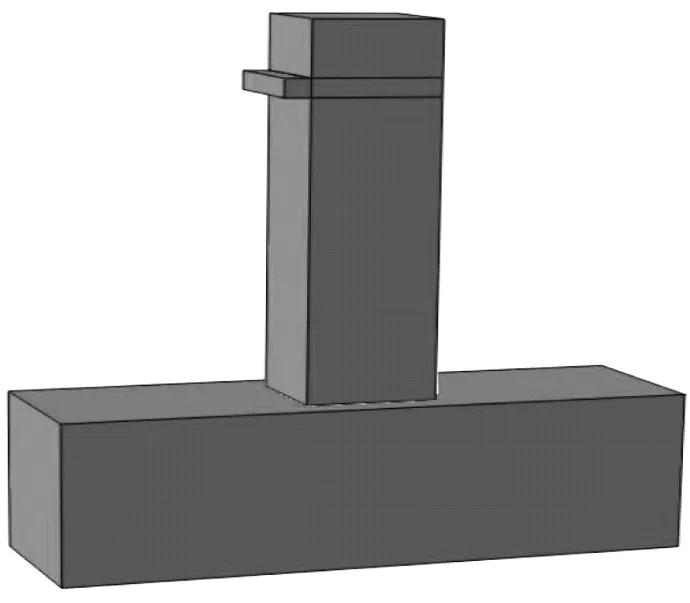
(a) 混凝土有限元模型(b) 钢筋骨架有限元模型图5 有限元模型Fig.5 Finite element model

2.3 单元类型及网格划分

根据模型变形及受力特点，混凝土选用八节点减缩积分格式的线性六面体单元C3D8R，钢筋骨架(箍筋和纵筋)采用两节点线性三维桁架单元T3D2。在有限元分析中，网格划分直接影响分析计算时间和分析结果精度，经过多次试算，在精度与计算收敛之间达到平衡，模型混凝土尺寸取30 mm，钢筋单元长度取13 mm,混凝土模型单元网格采用扫掠中性轴算法，由ABAQUS自动生成相应的网格单元。

3 有限元结果验证与分析

为验证数值模拟得到滞回曲线的准确性，根据试验中CCSRC-1*、CCSRC-3*、CCSRC-6*试件建立模型，将试验得到的滞回曲线与数值模拟结果做对比(如图6)，同时以CCSRC-3*为例，将构件损伤云图提出，对比其破坏形态(如图7)。

(1) 从图6中可以看出两者滞回曲线基本相同，卸载刚度一致，最大水平承载力从表4计算知平均误差为3.3%，正负方向荷载下降相比试验偏快；从图7可以看出有限元分析结束时，柱底部混凝土损伤较大且发生严重的变形，同时从CCSRC-3*极限破坏形态来看柱底两侧混凝土达到极限压应变而被压碎脱落，发生弯曲破坏，两者破坏形态较为一致。

(2) 数值模拟与试验结果相比：有限元计算的荷载位移曲线正反向较为对称,而试验曲线在反向加载时高于正向加载,可能原因有限元分析过程中试件的固定与位移加载较为准确，而在实际试验过程中试件制作安装与加载都存在偶然误差所导致的；试验滞回曲线下降段相对与数值模拟较为平缓，主要是由于有限元分析时钢筋本构模型采用双线性，导致有限元模拟过程中钢筋损伤累积相对于试验偏大，致使计算结果延性降低；计算结果的初始刚度较试验偏大，可能由于未考虑钢筋与混凝土之间的黏结滑移，且材料本构模型中材料的损伤与刚度退化都较为理想化，这与实际试验有所区别。

(3) 从表4及图7可以看出的模拟结果与试验结果基本吻合，表明有限元分析采用的材料本构关系及子程序可以体现出焊接环式箍筋约束混凝土柱在拟静力试验下的受力特点，能够反映不同参数下构件抗震性能。因此可以认为有限元模拟的结果具有较高的可靠性。

表4 试验与模拟承载力对比

图6 试验与模拟结果对比图

图7 破坏形态对比Fig.7 Comparison of failure patterns

4 扩大参数分析

为保证试验与模拟结果的准确性，尽可能减少其他因素的干扰，采用CCSRC-1*模型的各项数据，设计9个构件，与试验结果共同分析，探讨轴压比、配筋率对其抗震性能的影响规律。构件主要设计参数如表5。

5 抗震性能分析

5.1 滞回性能

5.1.1 滞回曲线

杨勇等[7]在对焊接箍筋混凝土框架柱抗震性能研究中发现在配箍率相同的情况下，随着试件轴压比降低，滞回曲线越来越饱满，耗能能力增强。为本文焊接环式箍筋约束高强混凝土柱的相应研究提供参考。

通过ABAQUS软件对所有有限元模型进行分析计算，将部分滞回曲线给出(如图8)；将试验得到的不同参数下试件的滞回曲线给出(图9)，一同进行分析与归纳，来增加本文所得出结论的可信度与准确性。

表5 构件的主要设计参数

(1) 通过对图8各构件滞回曲线计算分析可知：轴压比小的构件(CCSRC-4、CCSRC-10)，滞回曲线丰满且较为稳定；而轴压比大的构件(CCSRC-6、CCSRC-12)，其滞回曲线较为扁平；可以得出：随着轴压比的提高，构件耗能能力降低。

(2) 同时分别对图8的CCSRC-4和CCSRC-10、CCSRC-5和CCSRC-11、CCSRC-6和CCSRC-12对比分析：轴压比一定时，配箍率大的构件，在不同位移下的滞回环较好；配筋率较小的构件，其滞回曲线整体饱满度较差，耗能能力显著下降。

(3) 以上模拟得出的结论在试验滞回曲线图中得到很好的验证：CCSRC-1*(n=0.33)滞回曲线较为饱满，每次循环抗剪承载力衰减较慢，滞回曲线稳定；而CCSRC-4*(n=0.53)滞回环较差，滞回曲线下降段明显变陡；观察试验CCSRC-4*(ρV=2.28%)、CCSRC-5*(ρV=1.79%)、CCSRC-6*(ρV=1.39%)可以看出：配箍率较大的试件，其滞回曲线饱满，承载力衰减慢，抗震性能有较大的提升。

图8 各构件模拟滞回曲线Fig.8 Each member simulates hysteretic curve

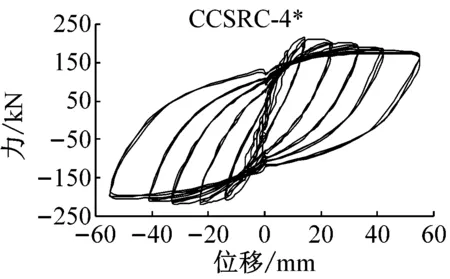
图9 各试件试验滞回曲线Fig.9 Test hysteresis curves of each specime

5.1.2 骨架曲线

骨架曲线可宏观反映出试件的各特征点的位移和荷载、延性、强度退化和刚度退化等抗震性能[8]。颜军等[9]通过对焊接封闭箍筋混凝土柱拟静力试验，分析不同轴压比下各柱的骨架曲线得到随着轴压比的增大,试件承载能力增大,但极限位移值越小,变形能力越差,延性降低越明显。

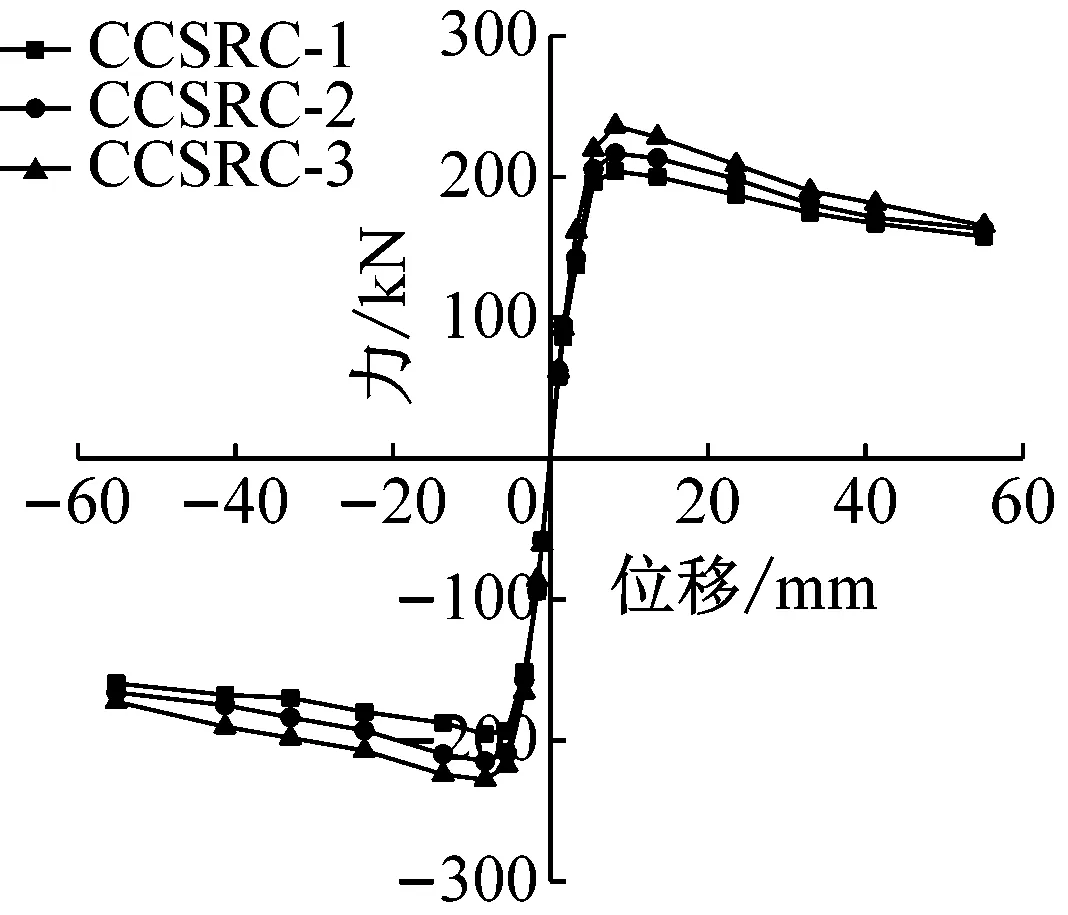
整理六个试件的数据，绘制骨架曲线(如图10)。并分析数值模拟的数据,得到的骨架曲线(如图11)，来探究轴压比、配筋率对骨架曲线的影响，与试验结果互相验证，并一同分析得出结论。从图10和11可看出：

图10 各试件骨架曲线Fig.10 Skeleton curve of each specimen

(1) 从本试验也可以看出在配箍率一定的情况下，随着轴压比的增大，骨架曲线在达到最大水平承载力后下降速度加快。从图11(a)知试件的承载力由CCSRC-1的204 kN增大到CCSRC-3的237 kN，增大了16.2%；从图11(b)可知试件的承载力由CCSRC-4的202 kN增大到CCSRC-6的233 kN，增大了15.3%；从图11(c)的结果知道试件承载力由CCSRC-7的198 kN增大到CCSRC-9的227 kN，增大了14.6%，可得出结论：轴压比越大，构件最大水平承载力也随之增大。

(2) 在轴压比一定时，高配箍率的构件在骨架曲线强度下降段表现得更加平缓。从图11(d)可知试件的承载力由CCSRC-7的198 kN增大到CCSRC-1的204 kN，增大3.0%；从图11(e)中知试件承载力由CCSRC-8的213 kN增大到CCSRC-2的216 kN，增大了1.4%；在图11(f)中试件承载力由CCSRC-9的227 kN增大到CCSRC-3的237 kN，增大了4.4%。可知随着配箍率的增大，构件最大水平承载力也增大。

(3) 由上述对比结果可得出轴压比对构件最大承载力的影响要强于配箍率，这一点也可从实际试验中得以验证：CCSRC-1*(ρV=2.28%、n=0.33)根据试验结果可知最大承载力为187 kN，而CCSRC-3*(ρV=1.39%、n=0.42)最大承载力为208 kN，增大了11.2%。

(a)(b)(c)

(d)(e)(f)图11 各构件骨架曲线对比Fig.11 Comparison of skeleton curves of various components

5.2 刚度退化

为了研究构件在低周反复荷载下的刚度退化规律，参考文献[10]，将刚度定义为各构件在每级荷载下的割线刚度，表达式如下

(4)

式中：Ki为第i次循环的割线刚度平均值；-Fi为第i次循环反向加载的水平峰值荷载；+Fi为第i次循环正向加载的水平峰值荷载；-Xi为第i次循环反向加载水平峰值荷载对应的位移；+Xi为第i次循环正向加载水平峰值荷载对应的位移。

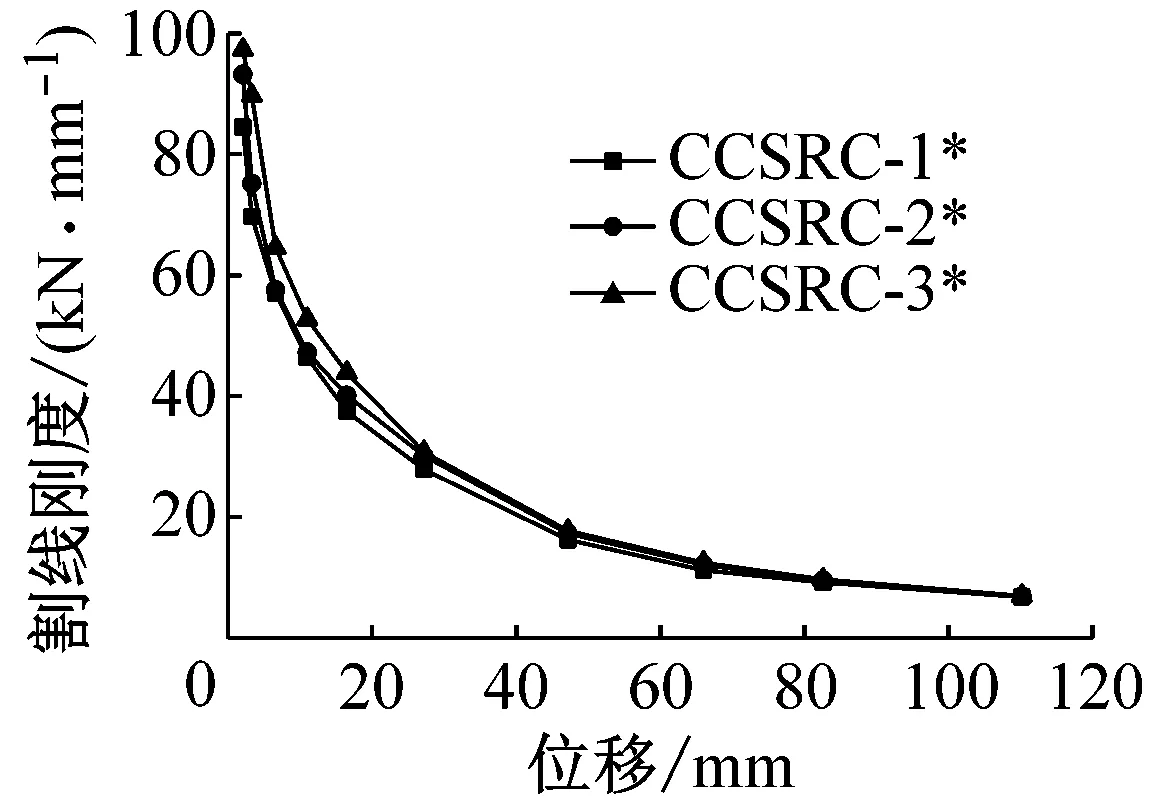
根据以上计算结果(图12)来探讨轴压比、配筋率对构件刚度退化的影响。由图12可知，各试件均未出现突然的刚度下降，表现出较为平稳的刚度退化，说明焊接环式箍筋约束高强混凝土柱在低周反复荷载作用下的损伤发展较平稳[11]。

(1) 从图12(a)可知：CCSRC-1*、CCSRC-2*、CCSRC-3*都是在较低轴压比下进行试验，相较于后三组，整体割线刚度都有着明显下降。

(2) 从图12(b)可以看出：当轴压比基本相同时，配筋率越大的试件,在加载初期刚度较大 但其刚度退化也越快,屈服荷载以后的刚度退化越缓慢。

(3) 从图12(c)、(d)、(e)可以看出：在配筋率一定的情况下，在加载初期，随着轴压比的增大，构件的割线刚度也随之增大，但在加载后期，轴压比小的构件刚度衰减较慢，曲线表现较为平稳，轴压比大的构件刚度退化速率较快，具体表现为在最后一次位移加载之后，轴压比大的构件割线刚度与轴压比小的构件还小；但随着配筋率的减小，改变轴压比，构件的割线刚度曲线分化越不明显。

5.3 延性分析

张兴虎等[12]以轴压比为参数对高强螺旋箍筋约束混凝土柱进行抗震性能研究发现轴压比是影响试件延性性能的主要因素之一，轴压比越高，高强螺旋箍筋约束混凝土柱延性性能越差。

本文采用位移延性系数来定量分析配筋率、轴压比对试件延性的影响。位移延性系数表达式如下

(a)(b)(c)

(d)(e)图12 不同参数下试件的割线刚度对比Fig.12 Comparison of secant stiffness of specimens under different parameters

(5)

式中:u为位移延性系数；Δu为极限位移，取最大水平力下降到85%时对应的位移；Δy为屈服位移,各构件的屈服位移采用等能量法[13]确定，具体计算方法见图13，根据试验结果，将每根柱子的位移延性系数计算并整理见表6。

(1) 根据规范规定，普通钢筋混凝土柱的极限位移角为0.02，但根据计算焊接封闭箍筋约束高强混凝土极限位移角均远大于0.02，说明此种构件延性较好，抗倾覆能力强，具有良好的抗震性能。

图13 计算示意图Fig.13 Schematic diagram

表6 加载过程骨架曲线特征点计算结果

(2) 对比CCSRC-1*和CCSRC-4*、CCSRC-2*和CCSRC-5*、CCSRC-3*和CCSRC-6*，发现柱子的延性分别增大21.4%、16.3%、20.4%，可以看出在配筋率一定的情况下，轴压比较低时，极限位移较大，变形能力强，具有良好的延性。虽然随着轴力增大，对构件前期割线刚度有一定提高，到加载后期，由于P-Δ效应等因素的影响，构件承载力衰减加快，延性随之下降。

(3) 分析CCSRC-4*、CCSRC-5*和CCSRC-6*，在轴压比基本相同情况下，试件配筋率由CCSRC-6的ρV=1.39%增大到CCSRC-4的ρV=2.28%时，延性由4.83变为5.79，增大19.8%。由此可知：提高配筋率可以有效改善构件的延性。主要因构件达到最大水平承载力之后，箍筋约束核心混凝土的横向变形，使其进入三向受力状态，导致其有较高变形能力，延性得以提高。

(4) 对表6数据进行分析：较高轴压比可以延缓柱子裂缝的出现，且对柱子的延性有着明显的降低作用，从表中知道CCSRC-4*配筋率即使为2.28%，但其延性为5.79，与配筋率为1.39%的CCSRC-3*的延性5.82，只相差0.03，说明在高轴压比情况下，提高配筋率对试件延性提高作用较小。

5.4 耗能性能

耗能能力是评价构件抗震性能的重要指标。李升才等[14]在高轴压比下对密置密置焊接环式高强复合箍筋约束高强混凝土柱进行抗震性能研究，通过对不同轴压比下柱子的等效黏滞系数计算发现随着轴压比的增大,等效黏滞阻尼比减小,耗能性能变差。本文采用同样方法，用等效黏滞系数he来定量描述构件的耗能能力。选取屈服后构件五个位移幅值级数(1/50、1/35、1/25、1/20、1/15)，来计算构件每个滞回环的等效黏滞系数，将数值模拟与实验结果整理，如图14。he的计算简图如图15，等效黏滞系数计算he计算方法如下

(6)

式中：SECF和SEDF为椭圆阴影部分面积;SADO和SBCO为三角形面积。

(a)(b)(c)

(d)(e)(f)

(g)(h)(i)图14 等效阻尼系数对比Fig.14 Comparison of equivalent damping coefficients

图15 计算简图Fig.15 Calculation diagram

从图14中可知,构件等效黏滞系数随着幅值的增大而增大，表示耗能能力逐渐增加，且随着加载位移的增大，增幅逐渐降低，主要是由于随着加载位移的不断增大，受力区混凝土损伤加剧，逐渐退出受力工作，内部纵向钢筋开始发挥作用，致使弹性变形占总变形的比例增大，故其增幅逐渐降低；对图14的(a)、(b)、(c)、(i)进行分析可知：随着轴压比的增大，构件在各个加载级数的等效黏滞系数整体下降，耗能能力越来越差；观察图14的(d)、(e)、(f)、(h)可以得到：配筋率对构件耗能能力有着一定的影响，配筋率越大，等效黏滞系数就越大，即构件耗能能力就越强。利用试验结果即图14的(g)可知：在轴压比增大，配箍率降低的情况下，构件的等效黏滞系数降低，耗能能力变差，与前述结论一致。从图中可知构件在屈服后每级加载等效耗能系数均大于0.3，说明焊接环式箍筋约束高强混凝土柱有良好的耗能能力。

6 抗震承载力公式

(1) Priestley等[15]通过研究循环荷载作用下钢筋混凝土柱的抗剪强度，认为柱抗剪强度由混凝土提供的抗剪强度Vc；横向约束钢筋下形成的析架提供的抗剪强度Vs；在柱子上的轴力所形成的拱机构所提供的抗剪强度Vp，即钢筋混凝土柱抗剪强度为这三者抗剪强度贡献的总和。

(2) 在建立焊接环式箍筋约束高强混凝土抗剪计算公式时，主要参考规范GB 50010—2002的格式和参数，采用有限元数据进行回归分析得到关键参数，利用试验数据验证公式的正确性。本文以扩大参数的9组模拟数据为基础，将继续设计6个不同构件，来保证公式的可靠性，一共15个构件，进行回归分析，新设计构件参数见表7。

表7 构件的主要设计参数

(3) 对于焊接环式箍筋约束高强混凝土柱，其抗剪承载力Vh和普通混凝土柱相似，仍然有三部分构成，主要是混凝土提供的抗剪承载力Vc、箍筋提供的的抗剪承载力Vs和轴力提供的抗剪承载力Vn，格式如下

Vh=Vc+Vs+Vn

(7)

(4) 对于普通混凝土柱来说，规范中认为轴力N对抗剪承载力影响较小，通过将轴力乘以一个系数来表现这种影响，且对于轴力做出规定：当N<0.3fcA时，取N值；当N>0.3fcA时，取N=0.3fcA。此处A为构件的截面面积。通过试验与数值模拟可知，此种做法与本结构的试验结果有所差别，轴压比在此种结构中对抗剪承载力有着较大的贡献，因此查阅文献[16]，利用拱机构剪力传递机制，假定受压区高度为h/2，这样轴力的合力作用在受压区形心处，由平衡条件可得

(8)

(5) 由于箍筋在钢筋混凝土梁与钢筋混凝土柱中作用机理相似，因此参考规范GB 50010—2002中，箍筋在本结构中的对抗剪承载力的影响依旧取

(9)

其中AyV=nAyV1，分析焊接环式箍筋结构与传统斜截面受剪机理的桁架模型可知，外环箍在构件抗剪承载力的提高中发挥主要作用；对于内环箍来说，它能充分发挥箍筋的径向约束力，提高混凝土部分的抗剪能力，但在箍筋部分的抗剪能力上，作用相对较小，故n取2；由于内环箍的存在限制了外环箍的发展，而且在柱达到最大水平承载力时，与裂缝相交的箍筋达到了屈服强度，但要考虑拉应力可能不均匀，特别是靠近剪压区的箍筋可能达不到屈服强度，考虑以上因素对箍筋强度进行折减，折减系数为0.7，即fyV1=0.7fyV；在低周往复荷载作用下，由于混凝土损伤、退化，导致横向钢筋的锚固下降和丧失，从而降低桁架模型所提供的抗剪能力[17]，从试验结果来看，配箍率越大，箍筋间距越小，此种影响就越明显，因此引入与箍筋间距有关的影响因子β，对箍筋抗剪能力的数学模型进行修正。

(6) 对于焊接环式箍筋约束高强混凝土柱来说，其较普通混凝土柱对核心混凝土约束强，根据规范规定，参考普通混凝土柱混凝土部分抗剪承载力公式，通过模拟结果进行回归分析，对混凝土部分抗剪承载力的系数α进行修正，对于剪跨比λ的修正由于缺乏试验数据，因此依然采用规范规定即可。

(7) 综上所述并参考规范，建立焊接环式箍筋约束高强混凝土柱的抗剪承载力公式如下

(10)

式中：λ为剪跨比；α为混凝土部分抗剪承载力的系数；ft为混凝土抗拉强度设计值；s为箍筋间距。

由以上公式为基础，利用数值模拟数据，进行回归分析和修正，对于此种结构，建议采用以下公式进行抗剪承载力计算

(11)

式中：β的取值与箍筋间距有关，根据实验结果回归分析可定义：当箍筋间距s=55时，β取值为0.5，当箍筋间距s≥100，β取值为1，当箍筋间距介于二者之间，采用线性内插法。

(8) 为验证公式的正确性，利用本文回归分析得到的焊接环式箍筋约束高强混凝土柱抗剪承载力公式，计算每根柱的抗剪承载力，与试验结果进行对比，具体见表8。从表中可以看出规范公式所得结果平均值为0.915，变异系数为0.171，表明规范公式离散性较大，所得结果可靠度较低，普通混凝土柱抗剪承载力公式并不适用于焊接环形箍筋约束高强混凝土柱，而本文根据模拟数据回归分析所得公式的计算结果平均值为0.982，变异系数为0.028，相比规范公式，有了很大的改进，更加符合试验结果，表明本文建议公式具有更高的可靠度，可为设计人员提供科学的依据。

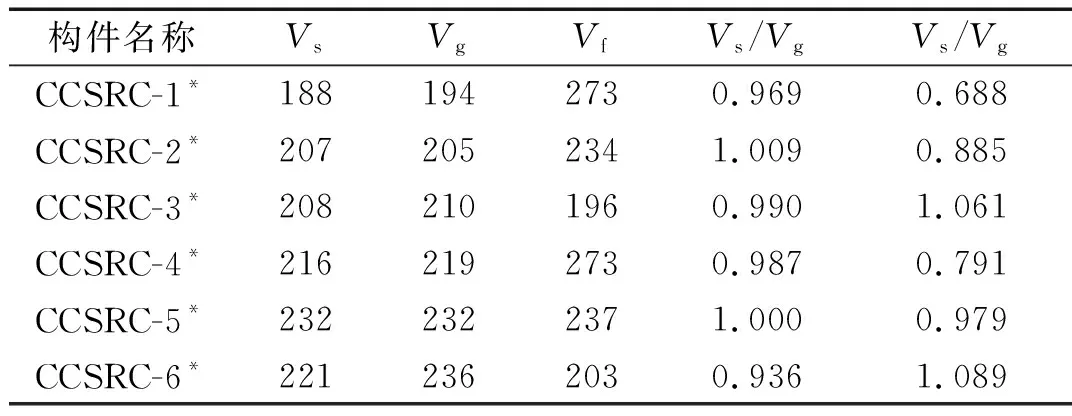
表8 两种抗剪公式计算结果对比

由表8可知：(1) 计算承载力所涉及的材料强度均为实测强度。

(2)Vs、Vg、Vf单位为kN；Vs代表试验测得的最大抗剪承载力；Vg为利用本文回归分析得出的抗剪承载力公式的计算值；Vf为参考规范GB 50010—2002中偏心受压构件斜截面受剪承载力公式的计算值，公式如下：

(12)

7 结 论

(1) 通过ABAQUS软件对焊接环式箍筋约束高强混凝土进行数值分析，与试验结果的滞回曲线进行对比，两者符合较好。

(2) 轴压比对构件的抗震性能影响较大。在配箍率一定的情况下，随着轴压比的增大，构件的承载力提高，极限位移变小，延性降低越发明显，耗能能力变差；轴压比大的构件在达到最大承载力之后，其下降过程较为陡峭，构件承载力有较大的下降。

(3) 通过分析配箍率的影响因素可以发现：轴压比一定时，配箍率大的构件其承载力也随之增大；随着配箍率的增大，构件的极限位移变大，延性变好，耗能能力增强；增大配箍率，构件承载力下降较为平缓。

(4) 本文通过查阅有关钢筋混凝土抗剪承载力文献，又结合混凝土结构设计规范，采用扩大参数有限元分析数据，回归得到有关焊接环形箍筋约束高强混凝土柱抗震承载力公式并利用试验结果进行验证，结果表明：本文提出公式与结果较为吻合，较之规范所提供的公式，精度有了很大提高，可为设计人员提供参考。