载体加速度对静电驱动微机械陀螺响应的影响分析

张利娟，张华彪，李欣业，王雅雪，于 涛

(1.河北工业大学 机械工程学院，天津 300134;2.天津职业技术师范大学 汽车与交通学院，天津 300222;3.天津商业大学 机械工程学院，天津 300134)

微机械陀螺由于其体积小、重量轻、制造成本低、易于批量生产、响应稳定等优点，广泛应用于航空航天、汽车、电子等领域[1-2]。微机械陀螺中非线性因素，如支承梁的非线性刚度、驱动/检测静电力等广泛存在，因此微机械陀螺的非线性动力学问题成为了近年来的研究热点。

Asokanthan等[3]研究了单轴振动微陀螺仪在输入角速度周期性波动下的非线性不稳定性。在角速度输入小幅周期波动的情况下，采用了一种基于平均法的渐近方法，得到了由参数共振引起的幅频特性曲线。Braghin等[4]考虑一个MEMS线振动陀螺，发现支撑梁的非线性硬化特性使得结构的共振峰向更高的频率弯曲。Martynenko等[5]研究了一种具有弹性杆的MEMS音叉陀螺仪，推导了敏感结构在运动基础上弯曲振动的非线性微分方程，采用渐近双尺度法研究了陀螺在运动基础上的非线性动力学问题。Mojahedi等[6]研究了微纳陀螺在直流电压和基础运动作用下的静态和动态的非线性响应。李欣业等[7-8]分别对简谐激励和参数激励的三次非线性刚度的微机械陀螺的动力学及时滞反馈控制进行研究，分析了系统参数和反馈增益及时滞对振幅和分岔特性的影响。尚慧琳等[9]研究了参数激励和立方非线性的切向梳齿驱动微陀螺，给出了Hopf分岔条件，揭示了系统参数对驱动和检测模态振幅和分岔行为的影响机制。文永蓬等[10]探讨了驱动微弹性梁和检测微弹性梁的非线性刚度对微陀螺输出的影响规律。郝淑英等[11-12]分析了驱动和检测刚度非线性对双检测微陀螺的幅频曲线、共振频率偏移的影响规律。Hamed等[13]研究了具有线性和非线性参数激励的微陀螺仪的动力学、能量传递和振动控制。Awrejcewicz等[14]研究了带扭转关节的微机械陀螺，考虑了刚度和关节非线性的影响，多尺度法分析了系统在主共振和内共振的情况的稳态响应。Tsai等[15]考虑了弯曲刚度非线性和静电力非线性，研究了的微陀螺仪在不同的驱动频率和固有频率下的不稳定区域，求解了系统的稳态周期响应。

在实际工作中，微机械陀螺的载体，如导弹、无人机等，在工作工程中往往需要进行复杂的机动动作，过载可达30倍～50倍重力加速度。载体的运动会导致微机械陀螺系统的响应发生变化，导致测量出现误差，甚至发生系统故障。Thakur等[16]利用简化耦合谐振器分析了载体加速度对含刚度误差的MEMS音叉陀螺输出的影响，并提出了减小加速度影响的建议。Ali[17]研究了时变的载体加速度和温度引起的微机械陀螺误差的补偿问题。Bancroft等[18]研究了人走路和跑步引起的微机械陀螺响应误差的补偿。已有研究主要针对载体运动影响的补偿和消除，并未涉及机理分析，非线性因素也未得到充分考虑。本文针对载体加速度对微机械陀螺系统的动力学响应的影响进行分析，考虑载体在微陀螺驱动和检测两方向的运动建立系统的动力学方程，重点关注载体加速度对微机械陀螺系统响应的影响。

1 考虑载体运动的微机械陀螺系统的动力学方程

考虑图1所示的微机械陀螺，图2是其等效弹簧质量模型，其中m为微陀螺的敏感质量，xa-oa-ya为绝对坐标系，微机械陀螺与载体固联，载体在绝对坐标系的水平和竖直方向分别有位移xb,yb，同时有绕铅垂轴的角位移θ；x-o-y为载体坐标系，x为微陀螺的驱动方向，y为检测方向，敏感质量沿驱动和检测方向的位移分别为x,y，则微机械陀螺敏感质量在绝对坐标系中的位移可表示为

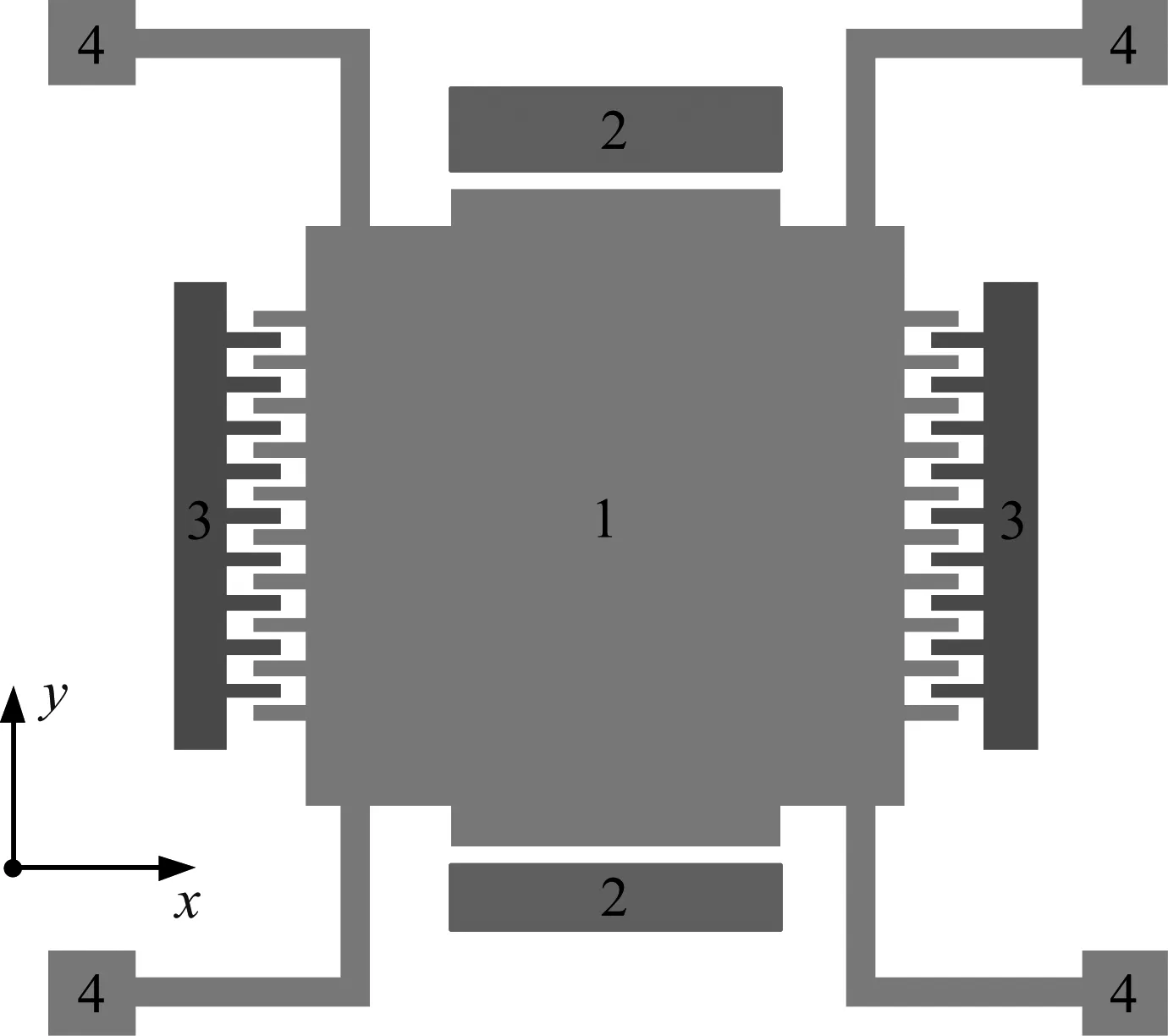
1-敏感质量;2-检测电极;3-驱动电极;4-锚点图1 微机械陀螺结构示意Fig.1 The schematic representation of MEMS gyroscope

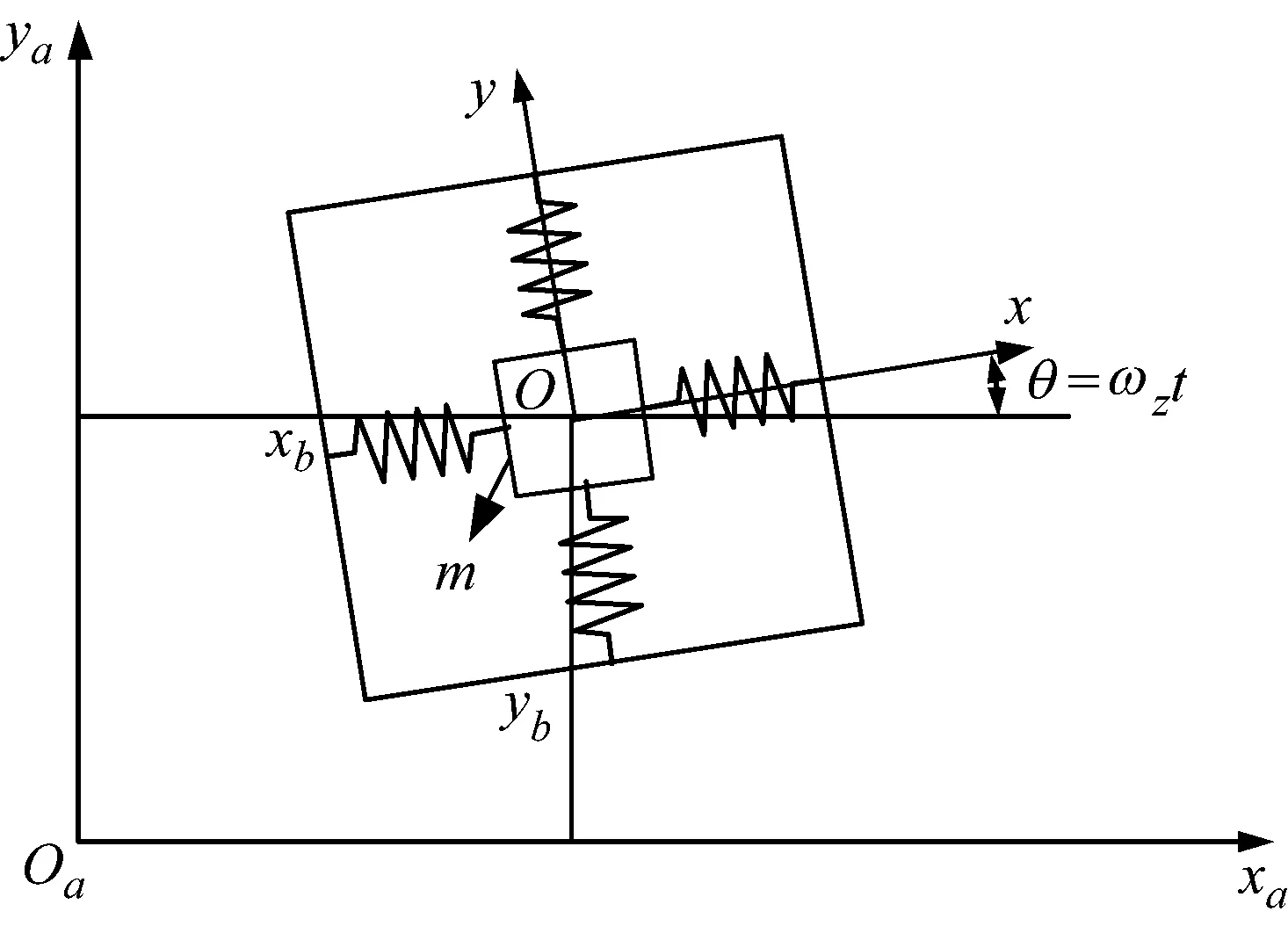
图2 微机械陀螺的等效弹簧质量模型Fig.2 Model of MEMS gyroscope as spring-mass system

xa=xcosθ-ysinθ+xb

ya=xsinθ+ycosθ+yb

(1)

其中θ=ωzt。对式(1)求导，可得敏感质量在绝对坐标系中的速度为

(2)

则敏感质量的动能为

(3)

考虑微机械陀螺的支承结构的三次非线性刚度，则其弹性势能为

(4)

考虑系统为真空封装，忽略气体阻尼，只考虑结构阻尼，则系统的瑞利耗散函数为

(5)

根据拉格朗日方程可求得微机械陀螺系统的动力学方程如下

(6)

其中,Fx,Fy分别为驱动和检测方向的静电力，其表达式如下[19]

Fx=Excosωt

(7)

其中

(8)

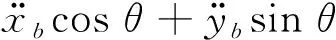
(9)

(10)

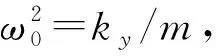
Y″+GX′+Y+βYY3+ξYY′+As-EYFY=0

其中G为无量纲陀螺力，βX,ξX和βY,ξY分别是驱动和检测方向的无量纲的非线性刚度系数和阻尼系数，Ad,As分别是载体在驱动和检测方向的无量纲加速度，EX,EY分别为驱动和检测电压相关的无量纲参数，上述无量纲参数表达式如下：

2 周期响应分析

本节利用谐波平衡法求解系统的周期响应。为初步了解系统周期响应的特征，首先对式(10)进行数值仿真，图3给出了Runge-Kutta法的计算结果，在载体有加速度时系统的振动响应偏离了平衡位置，因此设方程的解为

X=A0+A1cosΩτ+A2sinΩτ

Y=B0+B1cosΩτ+B2sinΩτ

(11)

注意到FY为分式项要将其展开为如下傅里叶级数形式方能进行计算。

FY=C0+C1cosΩτ+C2sinΩτ

(12)

其中

(13a)

(13b)

(13c)

这里采用留数定理[20]求解各展开项的系数，从而避免将FY展开为泰勒级数，引起不必要的误差。定义z=exp(iθ)，其中θ=Ωτ，则

(14)

将式(14)代入到式(13a)中，根据留数定理有

(15)

其中

zk为包含在单位圆内f(z)的孤立奇点。被积函数只有2个二级极点在单位圆内，分别是

(16)

于是有

k=1,2,m=2

(17)

将式(17)代入式(15)，可得

(18)

同理可求得

(19)

将式(11)和(12)代入式(10)，比较同次谐波系数有

(20)

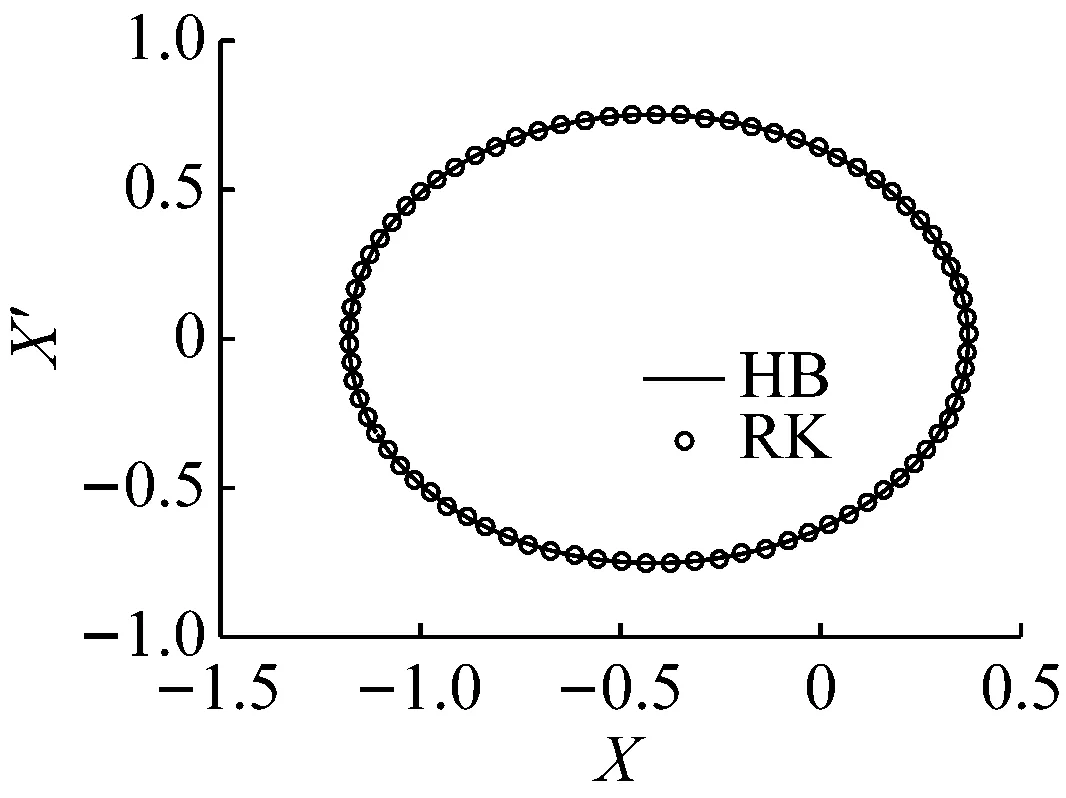
(a) EX=EY=0.04,Ad=0.4,As=0

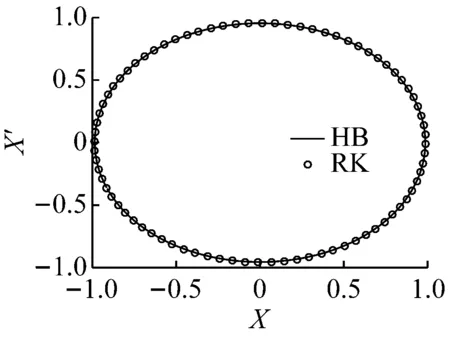
(b) EX=EY=0.04,Ad=0,As=0.4HB-谐波平衡法;RK-Runge-Kutta法图3 谐波平衡解与Runge-Kutta法数值解的对比Fig.3 Comparison of harmonic balance solution with numerical solution by Runge-Kutta method

3 载体加速度对系统响应特性的影响分析

幅频特性对于微机械陀螺至关重要，因此我们针对驱动和检测电压对系统幅频特性的影响进行了研究，图4和图5分别给出了驱动和检测电压对系统幅频特性的影响，可以看到检测电压的变化对幅频特性曲线的分岔形式影响很小；随着驱动电压的变化，系统在检测方向的幅频曲线出现了三种不同的分岔形式：① 没有静态分岔点的情况，如EX=0.01,EY=0.04时；② 幅频曲线峰值的右侧出现静态分岔点的情况，如EX=0.02,EY=0.04时；③ 幅频曲线峰值两侧都出现静态分岔点的情况，如EX=0.04,EY=0.04时。因此本文将考虑EX=0.01，EX=0.02，EX=0.04三种驱动电压情况(EY=0.04)，分别讨论载体加速度对系统响应特性的影响。

图6是驱动方向加速度对系统幅频特性的影响，可以看到在驱动方向的振幅随加速度增大而增大，检测方向的振幅随加速度的增大反而在减小。同时注意到在EX=0.01和EX=0.02时，幅频特性的分岔形式随加速度的变化没有发生改变，而在EX=0.04,Ad=0.4时，幅频特性峰值左侧的两个静态分岔点消失。为了说明驱动方向加速度对微陀螺性能的影响，图7给出了驱动方向加速度为不同值时，无量纲陀螺力对微陀螺检测振幅的影响，在载体没有加速度时，EX越大，影响曲线的斜率越大，即系统的灵敏度越大。随驱动方向加速度的增大，系统的灵敏度变小，且曲线的线性程度也发生了变化。

(a) EY=0.02

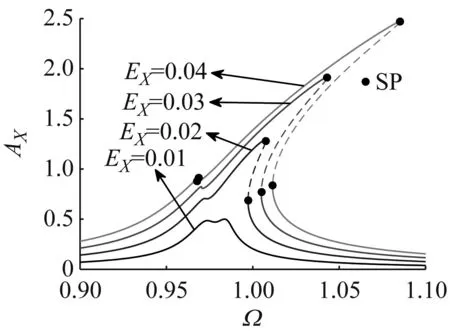
(b) EY=0.04SP-静态分岔点图4 驱动电压对微陀螺幅频特性的影响Fig.4 Effect of driving voltage on the amplitude-frequency characteristic of MEMS gyroscope

(a) EX=0.02

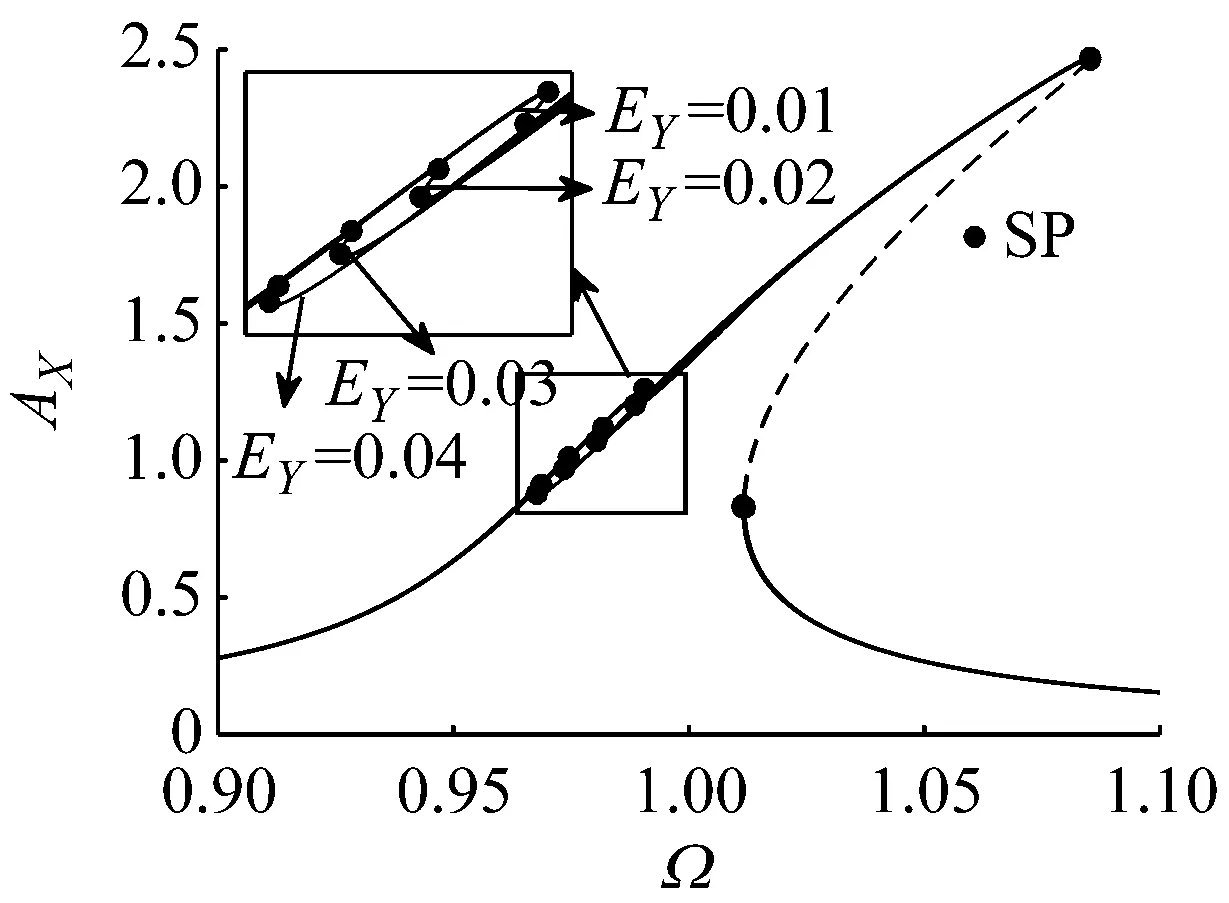
(b) EX=0.04图5 检测电压对微陀螺幅频特性的影响Fig.5 Effect of detecting voltage on the amplitude-frequency characteristic of MEMS gyroscope

为了精确分析载体加速度对系统响应零偏、灵敏度和非线性程度的影响。采用最小二乘法对上述曲线进行线性拟合，定义拟合方程为

AYp=SG+AB

(21)

其中S为灵敏度，AB为零偏，有

AB=AY(G=0)

(22)

同时将拟合后的曲线与原始曲线进行比较，定义非线性度为

(23)

显然图7中驱动方向的加速度没有引起零偏，图8是载体驱动方向加速度对系统灵敏度和非线性度的影响曲线，可以看到随驱动方向加速度的增大，系统的灵敏度逐渐降低。当EX=0.01和0.04时非线性度随加速度的增大整体趋势为减小，EX=0.02时非线性度随加速度的增大变化平缓。因此对于主要承受驱动方向加速度的微机械陀螺的设计，应主要考虑加速度对灵敏度的影响。

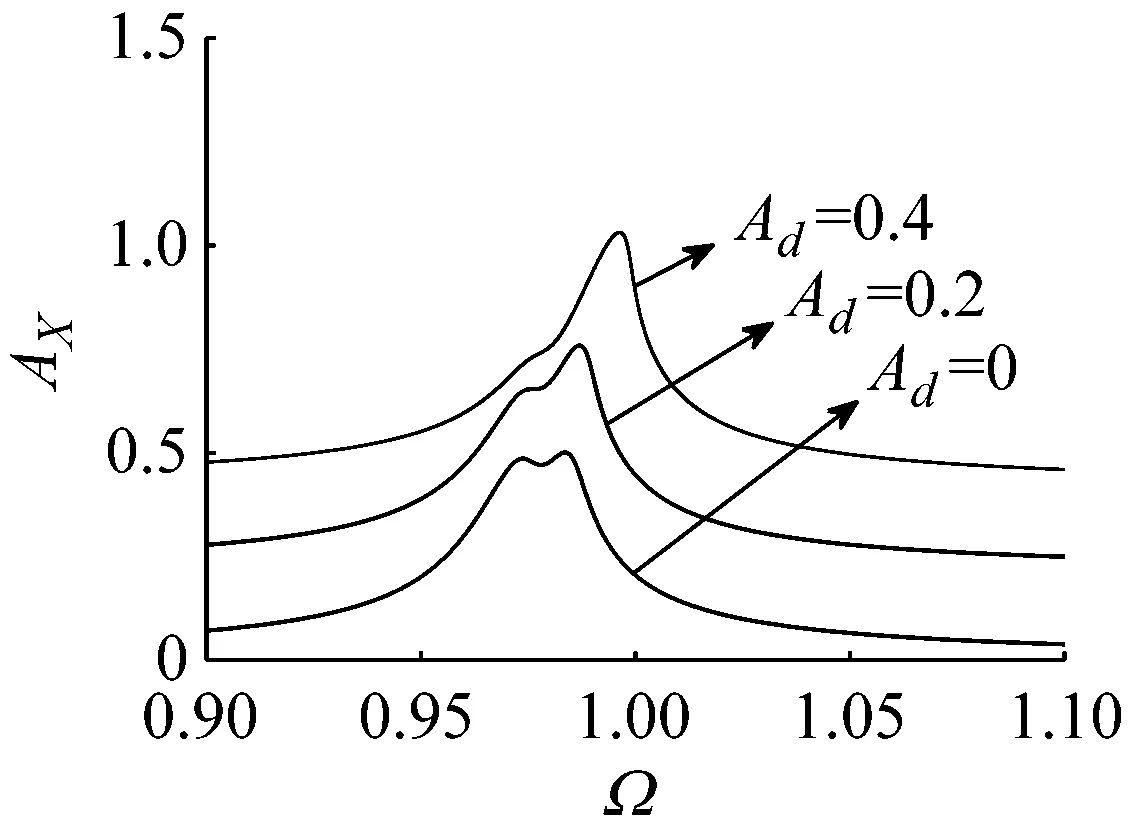
(a) EX=0.01(b) EX=0.02(c) EX=0.04图6 驱动方向加速度对系统幅频特性的影响EY=0.04Fig.6 Influence of driving acceleration on the amplitude-frequency characteristic

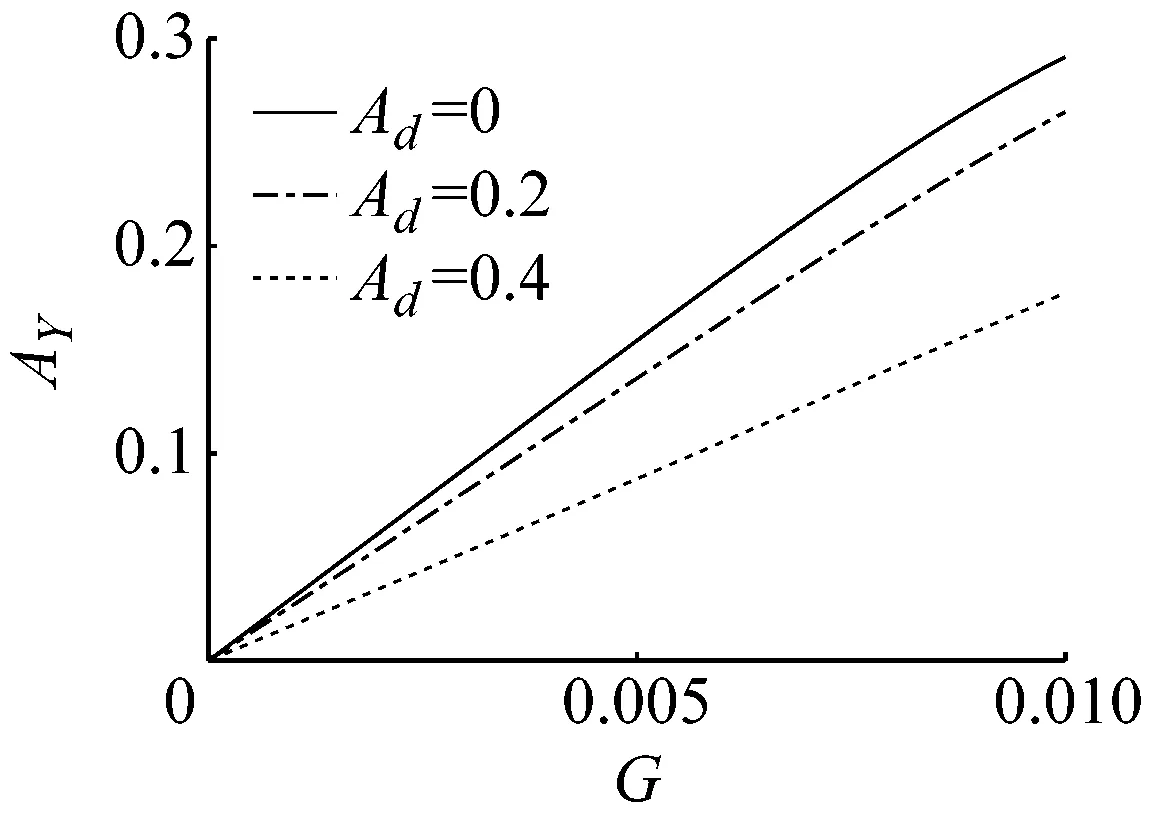
(a) EX=0.01(b) EX=0.02(c) EX=0.04图7 无量纲陀螺力对微陀螺检测振幅的影响Ω=0.975Fig.7 Effect of non-dimensional gyroscope force on detecting amplitude of MEMS gyroscope

图8 驱动方向加速度对灵敏度和非线性度的影响Fig.8 Effect of acceleration in detection direction on sensitivity and nonlinearity

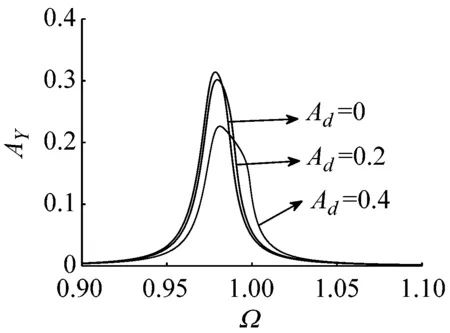
图9给出了检测方向加速度对系统幅频特性的影响，可以看到在EX=0.01时，驱动方向的峰值振幅随加速度增大而增大，而在EX=0.02和0.04时，检测方向加速度对驱动方向幅频特性的影响很小，其影响更多的体现在峰值左侧静态分岔点位置的变化。检测方向非共振区域的振幅随载体检测方向加速度的增大而增大，峰值振幅的变化则较为复杂。为了说明检测方向加速度对微陀螺性能的影响，图10给出了载体检测方向加速度为不同值时，无量纲陀螺力对微陀螺检测振幅的影响，在载体具有检测方向加速度的情况下，无量纲陀螺力为零时，系统的响应振幅也不为零，即系统出现了零偏；同时曲线的灵敏度和线性程度也随检测方向加速度的变化发生了改变。图11是检测方向加速度对系统零偏、灵敏度和非线性度的影响曲线，其中零偏随检测方向加速度线性增大，而且比例系数不受驱动电压变化的影响。EX=0.04时，系统灵敏度随检测加速度增大而减小，非线性度先增大后减小，而EX=0.01和0.02时，灵敏度在检测方向加速度较小时，随加速度变化平缓，非线性度的变化也较小；在检测方向加速度较大时，灵敏度急速降低，非线性度也发生了剧烈的变化。因此在载体承受的检测方向加速度较小时，可选取较小的驱动电压，并重点考虑零偏的补偿；而在载体承受的检测方向加速度较大时，需要同时考虑加速度对系统零偏、灵敏度和非线性度的影响。

(a) EX=0.01(b) EX=0.02(c) EX=0.04图9 检测方向加速度对系统幅频特性的影响Fig.9 Effect of detecting acceleration on the amplitude-frequency characteristic

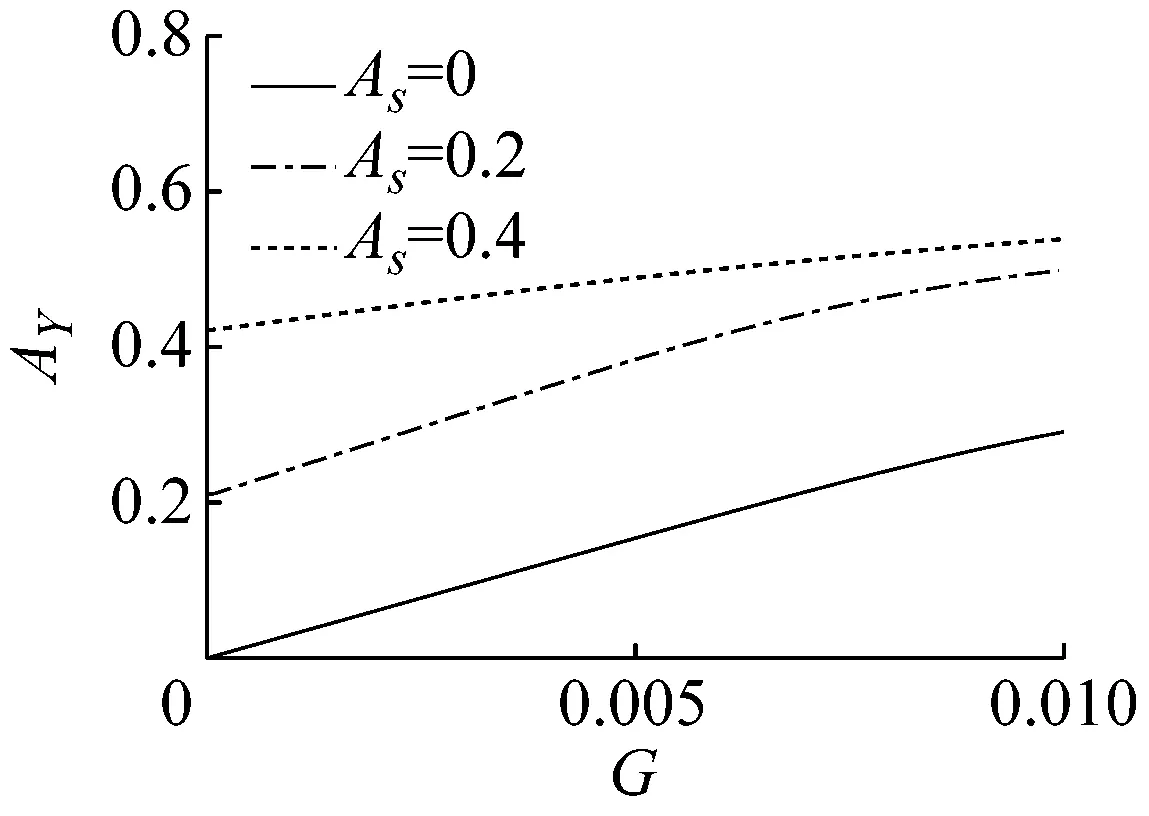
(a) EX=0.01(b) EX=0.02(c) EX=0.04图10 无量纲陀螺力对微陀螺检测振幅的影响Fig.10 Effect of non-dimensional gyroscope force on detecting amplitude of MEMS gyroscope

图11 检测方向加速度对零偏、灵敏度和非线性度的影响Fig.11 Effect of acceleration in detection direction on zero bias,sensitivity and nonlinearity

4 结 论

本文考虑非线性支承刚度、非线性的检测静电力，利用拉格朗日方程建立了微机械陀螺系统的动力学方程，针对载体加速度对微陀螺响应特性的影响开展研究。通过对系统的动力学方程进行数值仿真，发现载体的加速度会导致系统的振动响应偏离原始的平衡位置。利用谐波平衡法结合留数定理直接求解含分式项的动力学方程，得到了系统的周期响应，分析了驱动/检测载体加速度对系统幅频特性和性能参数的影响。研究发现驱动方向的加速度不会导致零偏，但会引起系统的灵敏度降低；检测方向的加速度会导致零偏的出现，零偏和检测方向加速度的大小成正比，但比例系数与驱动电压大小无关。系统驱动电压较小时，较小的检测方向加速度对系统的灵敏度和非线性度影响很小；而在驱动电压或者载体检测方向加速度较大时，系统的灵敏度急剧减小，且非线性度也发生了剧烈变化。