双段消能摇摆结构体系的地震反应特性研究

李国强，张文津，王彦博，孙飞飞

(1.同济大学 土木工程防灾国家重点试验室，上海 200092；2.同济大学 土木工程学院，上海 200092)

单段消能摇摆结构体系是一种抗震性能与可恢复性能良好的结构体系[1-5]，主要由四部分组成：主体结构、单段摇摆结构、耗能构件以及刚性连杆。主体结构承担了大部分的建筑使用功能，一般为框架结构。单段摇摆结构选用刚度较大的钢筋混凝土摇摆墙或摇摆钢桁架，附设于主体结构旁，可以控制各楼层发生均匀变形，遏制薄弱层的产生，提高整体结构的延性和承载力。耗能构件(如位移型阻尼器或速度型阻尼器)一般布设于摇摆结构变形较大的位置，高效耗能的同时将塑性损伤集中于局部区域，以便震后修复或更换。刚性连杆连接单段摇摆结构与主体结构，保证两者变形协调。

然而当主体结构高度较高时，为保证摇摆结构的整体刚度，需增大摇摆结构的截面，这有可能影响建筑的布置，并增加建造成本。2009年—2013年，Wiebe等[6-8]发现：如果在中间楼层位置将整片柱脚可抬起的摇摆钢桁架打断，通过自复位钢索牵引形成双段串联的摇摆结构，可以实现摇摆结构的分段设计，并且降低了高阶振型对于摇摆结构设计内力的影响。但Wiebe等的研究侧重于双段摇摆机制对高阶振型下地震作用的抑制效果，尚未关注双段摇摆结构对于高层建筑变形模式的控制作用。2010年，Psycharis[9]推导了双段串联的摇摆刚体在简谐激励下的动力响应。2016年，冯玉龙等[10]提出一种在屈曲约束支撑框架结构一侧附设连续摇摆结构的体系。2018年Ther[11]进一步研究了多段摇摆刚体的抗震性能，提出了考虑刚体间接触的理论算法，并通过振动台试验进行验证。既有研究表明，多段摇摆机制可以减小结构的地震响应，但是，多段摇摆结构对于主体框架各楼层变形的控制效果、多段摇摆机制应用于实际结构之后整体结构的抗震性能与抗倒塌性能，需要进一步研究。

为拓展消能摇摆结构体系对于高层建筑的适用性，减小高阶振型的影响，进一步提升主体结构的抗震性能，本文对双段消能摇摆结构体系进行了研究。采用有限元分析方法比较双段消能摇摆钢桁架-框架结构与传统支撑-框架结构、单段消能摇摆钢桁架-框架结构、单段摇摆钢桁架-框架结构、双段摇摆钢桁架-框架结构在地震作用下的弹塑性动力响应，研究了双段消能摇摆结构体系的抗震性能、可恢复性能与抗倒塌性能。

1 双段消能摇摆结构体系抗震机理

单段消能摇摆结构体系(single-rocking structure with dampers，SRD结构)存在两方面局限性：

(1) 适用高度的限制。随着结构高度的增加，摇摆结构的弯曲线刚度不断减小，对各楼层变形模式的控制效果不断减弱。为保障各楼层发生均匀变形，需提高摇摆结构截面的弯曲刚度，但这往往会占用较多的建筑空间，并增加建造成本。

(2) 摇摆结构的设计需求受高阶振型影响较大。地震作用下，单段摇摆结构控制主体框架各楼层的变形趋于线性，并抑制了高阶振型对应的变形模式。一阶振型所引起的地震作用对于摇摆结构设计内力的影响较小，而高阶振型的影响较大。

双段消能摇摆结构体系(dual-rocking structure with dampers，DRD结构)有望克服以上两方面局限性，如图1所示。DRD结构实质上是对SRD结构的一种改进：将单段摇摆结构在中间楼层位置分段为双段串联的摇摆结构，以位移型阻尼器(本文选用屈曲约束柱，buckling restrained column，BRC)连接两个分段摇摆结构，一对BRC的等效抗弯刚度按照与摇摆结构抗弯刚度相等的原则确定。小震下BRC不发生屈服，结构呈弯剪型变形，内力分布与传统支撑框架结构(brace frame structure，BRF结构)类似；中、大震下BRC屈服，上、下半段摇摆结构保持弹性并发生摇摆，分别控制上、下段主体框架均匀变形。

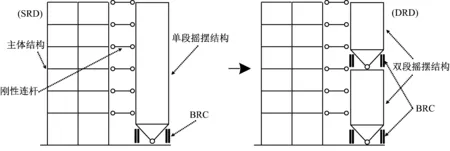
图1 双段消能摇摆结构体系

相比于SRD结构，DRD结构的优势主要体现在三个方面：

(1) 双段摇摆机制拓展了结构的适用高度。相比于单段摇摆结构，两个分段摇摆结构的弯曲线刚度提升近一倍，能够控制对应主体框架结构的变形更加均匀。高层建筑中，如果单段摇摆结构无法提供控制主体结构各楼层均匀变形所需的约束刚度，可以采用双段摇摆结构。

(2) 减小高阶振型对于摇摆结构设计内力的影响。摇摆结构与主体框架在各楼层位置通过刚性连杆(对应实际结构中的楼板)保持变形协调，图2给出了单段摇摆结构和双段摇摆结构对于主体框架前两阶振型控制机理的示意图。单段摇摆结构在抑制高阶振型、控制框架各楼层发生近似线性变形(趋于一阶振型)的同时，自身也会产生较大内力。将单段摇摆结构在中间楼层打断为双段摇摆结构，可以释放其与主体框架结构各阶振型形状之间的变形差，降低了双段摇摆结构内力水平。单段摇摆结构与框架一阶振型形状之间的变形差较小、与二阶振型形状之间的变形差较大，改进为双段摇摆结构之后，可显著降低主体框架二阶振型下摇摆结构的内力水平，对主体框架一阶振型下摇摆结构内力水平的影响相对较小。

(3) 双段消能摇摆结构体系可在更多位置布设阻尼器，耗能效率较单段消能摇摆结构体系有所提高。

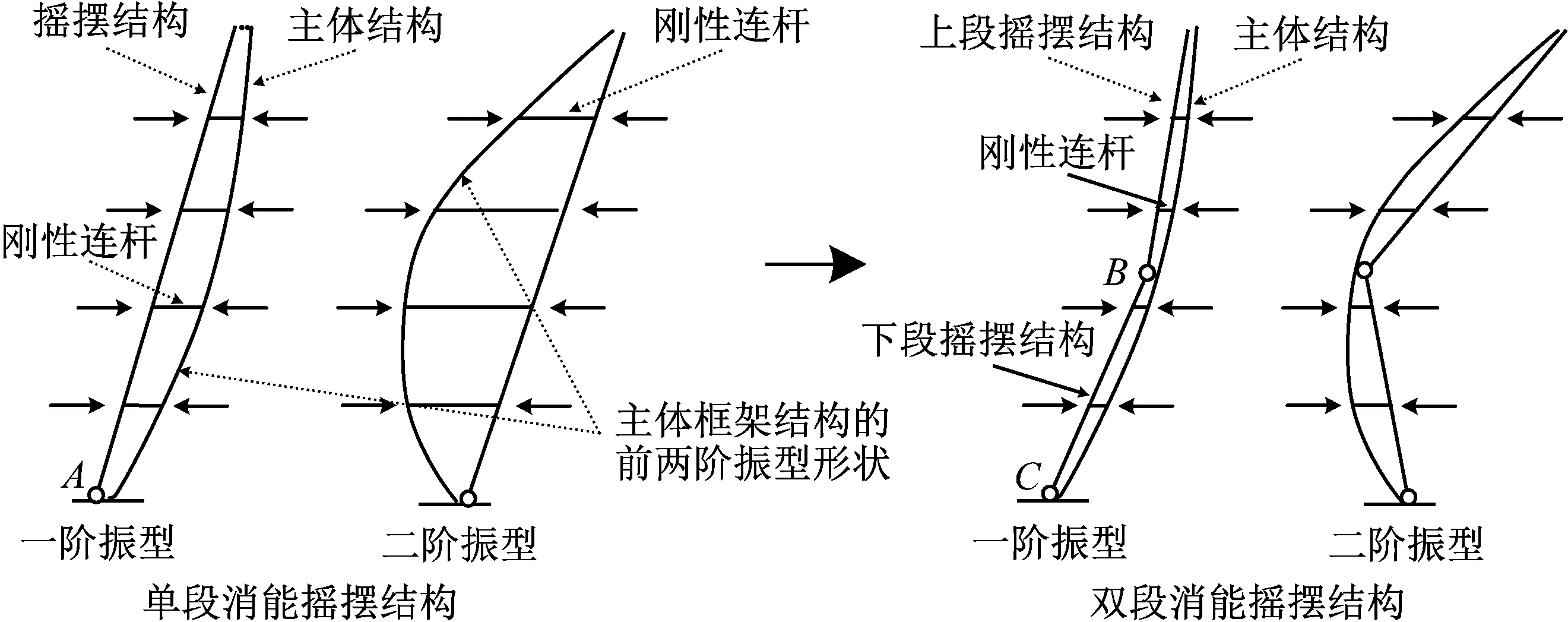
图2 双段摇摆结构对结构前两阶振型的控制

2 结构参数与计算模型

2.1 原型结构

根据我国GB 50011—2010《建筑抗震设计规范》[12]和GB 50017—2013《钢结构设计规范》[13]，设计了某20层支撑-框架结构(BRF结构)，图3(a)给出了结构示意图。设防烈度9度0.2g，场地类别III类第三组，特征周期0.65 s，楼面恒载6.0 kN/m2，活载2.0 kN/m2，经过归并后的构件截面信息如表1所示。钢材选用Q345，弹性模量为2.06×105MPa，泊松比为0.3。

仅以BRC替换BRF结构中支撑结构的底层柱，其余结构保持不变，可得到SRD结构，如图3(b)所示；仅以BRC替换BRF结构中支撑结构的底层柱和第11层柱，其余结构保持不变，可到DRD结构，如图3(c)所示；分别去除SRD结构、DRD结构中的BRC，即得到单段摇摆钢桁架-框架结构(single-rocking frame structure，SRF结构，见图3(d))和双段摇摆钢桁架-框架结构(dual-rocking frame structure，DRF结构，见图3(e))。

(a) BRF结构(b) SRD结构(c) DRD结构(d) SRF结构(e) DRF结构

表1 结构构件截面信息

2.2 弹塑性分析模型

采用OpenSees软件建立了BRF结构、SRF结构、DRF结构、SRD结构、DRD结构的弹塑性有限元分析模型。主体框架结构的梁、柱构件以及支撑结构的竖向构件使用基于力的梁柱单元(force-based beam-column element)模拟，通过纤维截面集成单元刚度矩阵。每根构件划分为四段，考虑材料非线性与重力二阶效应。

本文采用基于力的梁柱单元模拟其力学性能。两端为铰接。每根支撑划分为四段，初始缺陷按半波正弦的形式施加，幅值取构件长度的1/300，考虑材料非线性与几何非线性效应。按照以上支撑构件的建模方法，本文模拟了Black等[14]的试验，如图4所示，有限元分析结果与试验结果较吻合，OpenSees软件对于支撑构件的模拟能够准确反映其在往复荷载下的力学特性。为了保障摇摆结构具有足够的刚度和承载力，应通过设计保证摇摆结构的支撑杆件在地震作用下不发生屈曲，亦不进入屈服。

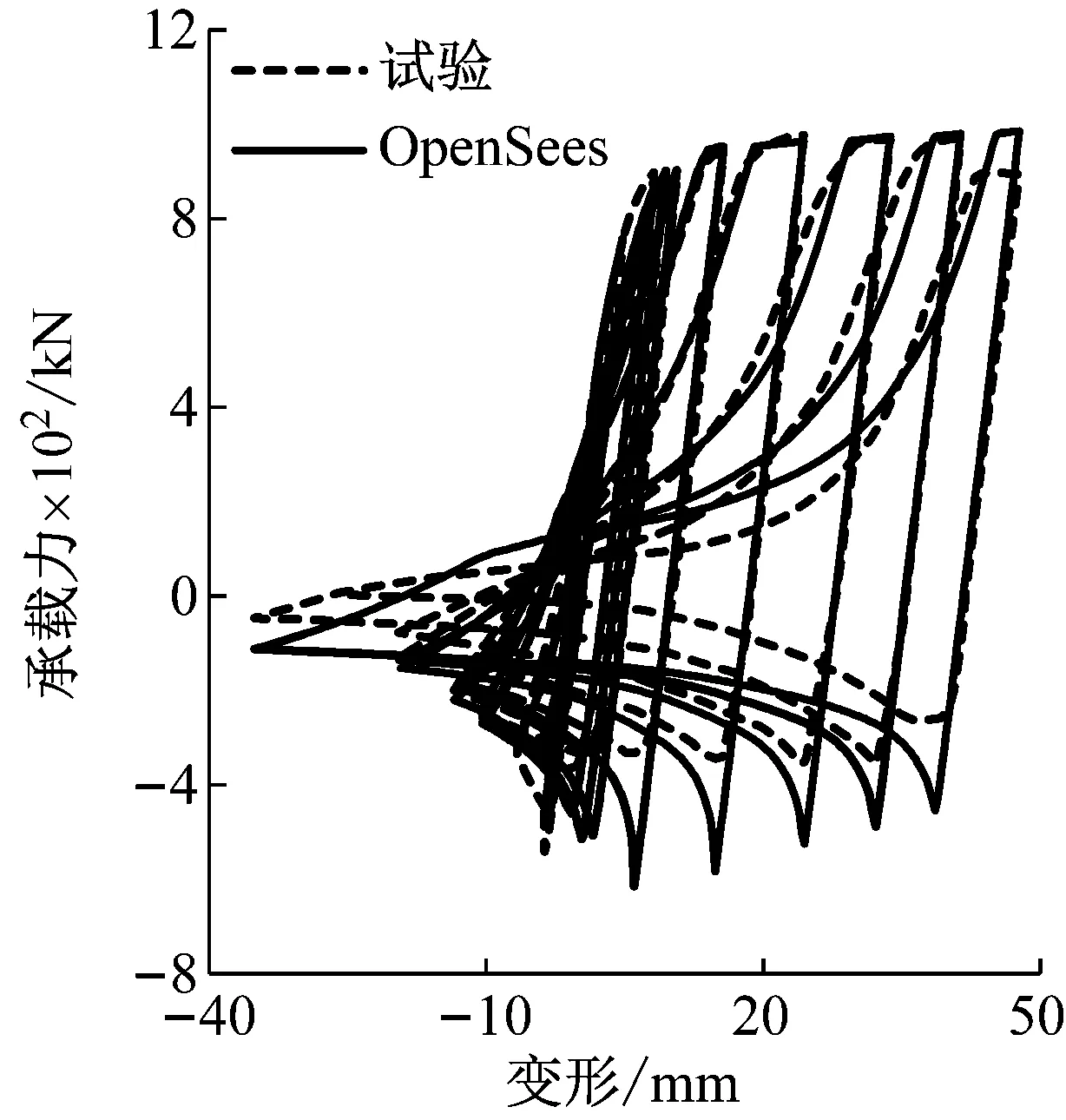
图4 支撑构件试验的有限元验证Fig.4 Finite element verification of brace test

Q345钢材使用双线性随动强化模型，BRC采用Giuffre-Menegotto-Pinto模型(OpenSees中Steel02模型)，服从等向强化规则。BRC以桁架单元(truss element)模拟，其弹性刚度与所替换支撑弦杆的轴向刚度相等。BRC相关设计参数如表2所示，滞回参数按照黄波等[15]的试验进行标定，如图5所示，结果较吻合。

表2 BRC设计参数

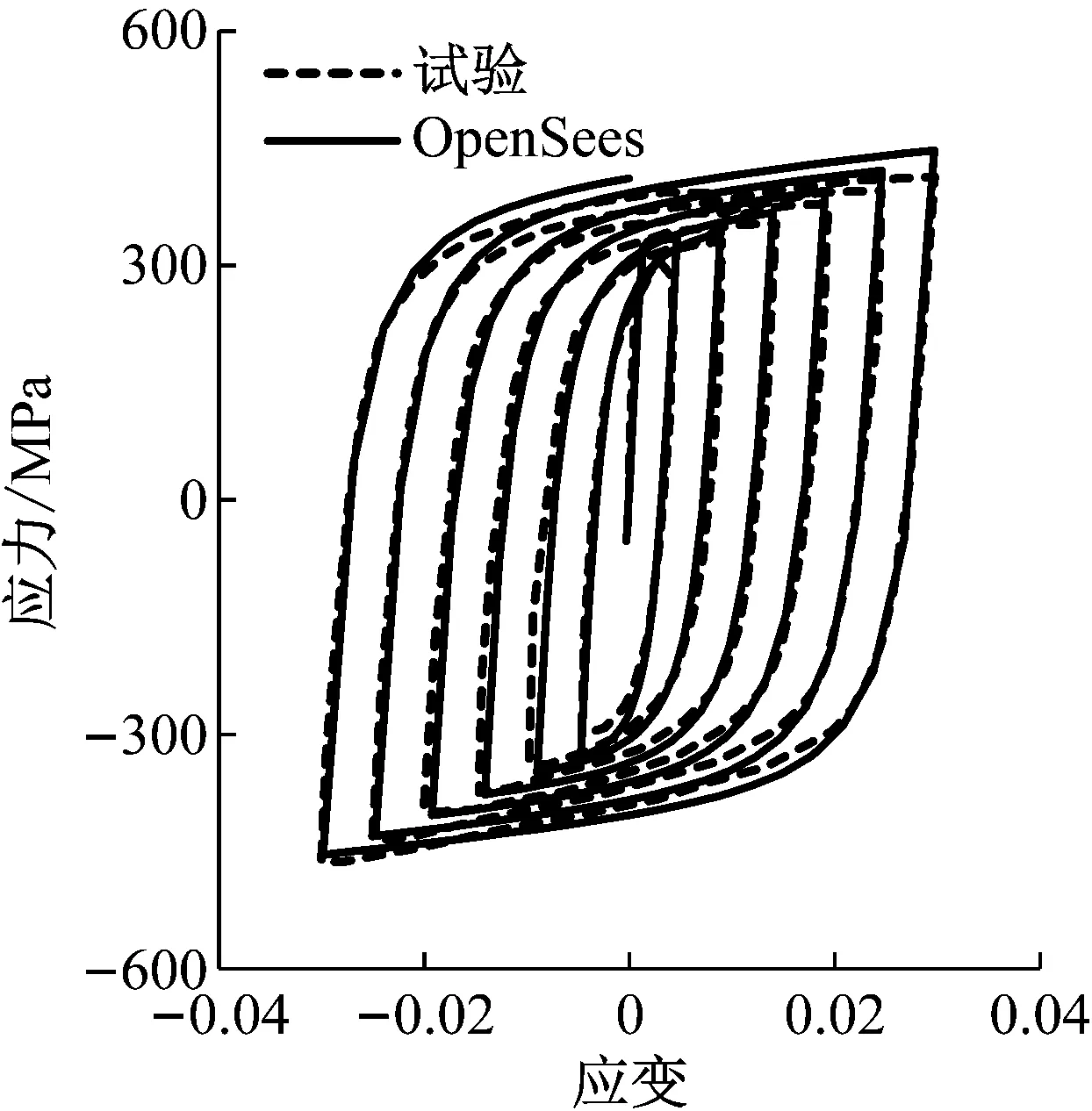
图5 BRC滞回参数的标定Fig.5 Calibration of hysteretic parameters of BRC

2.3 地震波

本文仅讨论罕遇地震作用下结构的弹塑性动力响应，从ATC-63[16]推荐的地震动记录集中选择8条地震动作为输入激励，地震动信息如表3所示。将峰值加速度(peak ground-motion acceleration，PGA)调幅至70 gal(设防地震)，8条波加速度反应谱如图6所示。

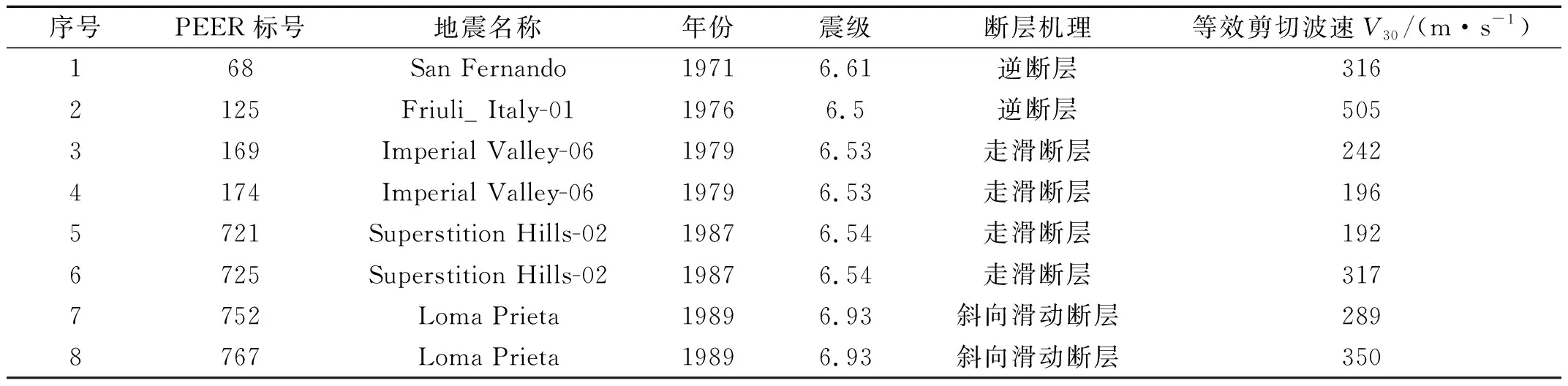
表3 时程分析所用的地震动记录集

3 结构弹塑性地震反应分析

3.1 静力推覆分析

对BRF结构、SRD结构、DRD结构、SRF结构和DRF结构进行模态分析，各结构的前三阶周期如表4所示。DRD结构与SRD结构前三阶周期完全一致，说明DRD结构的刚度与SRD结构刚度完全相同；DRD结构、SRD结构前三阶周期略大于BRF结构，说明DRD结构、SRD结构的刚度略小于BRF结构。

此外，BRC可以为结构提供弹性刚度，SRD结构的刚度大于SRF结构，且DRD结构的刚度大于DRF结构。由于双段摇摆结构对框架结构二阶振型的变形抑制作用显著减小，DRF结构的二阶模态刚度较SRF结构降低了29.3%。

各结构在推覆荷载作用下的承载力与对应的最大层间位移角如表4所示，图7给出了BRF结构、SRD结构、DRD结构、SRF结构和DRF结构在推覆荷载作用下基底剪力与最大层间位移角之间的关系曲线，可知：

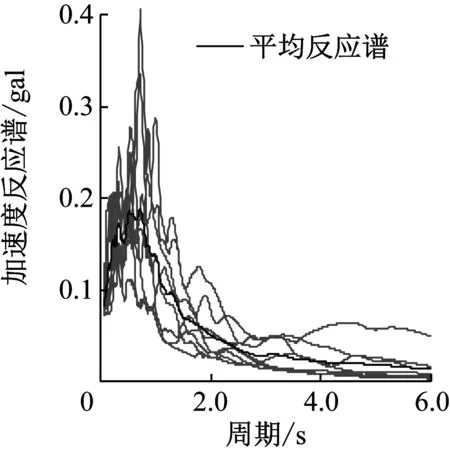
图6 地震动记录的加速度反应谱Fig.6 Acceleration spectrum of earthquake waves

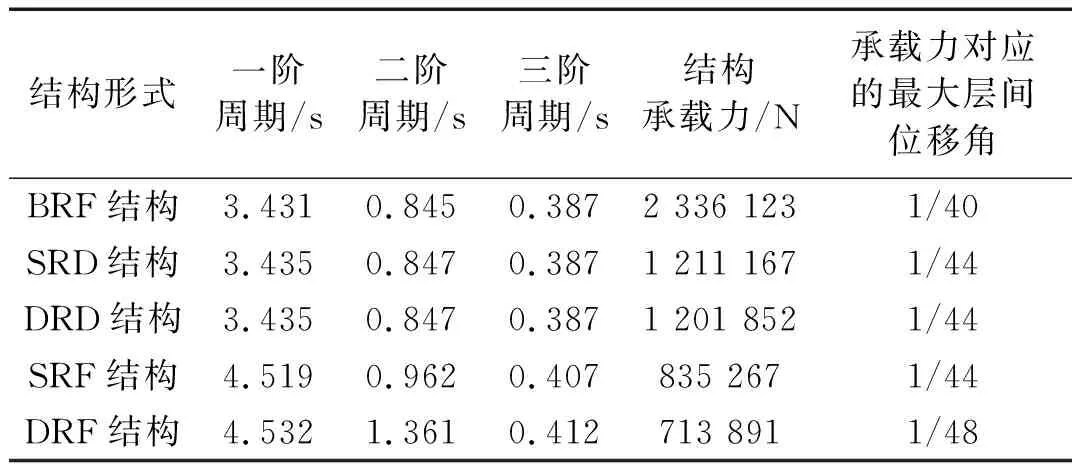
表4 各结构自振周期和静力推覆分析结果

(1) BRF结构承载力最高。BRC可以提高结构的抗侧刚度与承载力，SRD结构承载力大于SRF结构，且DRD结构承载力大于DRF结构。由于DRF结构在中部楼层被削弱，其承载力小于SRF结构。

(2) DRD结构的中部BRC不屈服、底部BRC屈服，其弹塑性抗侧刚度和承载力与SRD结构基本相当，承载力较BRF结构下降了48.6%。

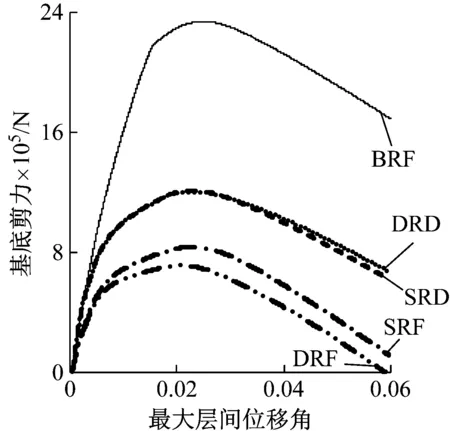
图7 结构基底剪力与最大层间位移角的关系Fig.7 Relationship between base shear force and peak story drift

3.2 弹塑性时程分析

按规范将8条地震动的峰值加速度(peak ground-motion acceleration，PGA)调幅至620 gal，研究BRF结构、SRD结构、DRD结构、SRF结构和DRF结构在罕遇地震下的弹塑性动力响应。图8给出了五种结构的地震响应，包括：最大层间位移角、残余层间位移角、最大结构楼层剪力、最大支撑构件轴力以及摇摆钢桁架的最大弦杆轴力。由图8可知：

(a) 最大层间位移角对比(b) 残余层间位移角对比(c) 结构楼层最大剪力对比

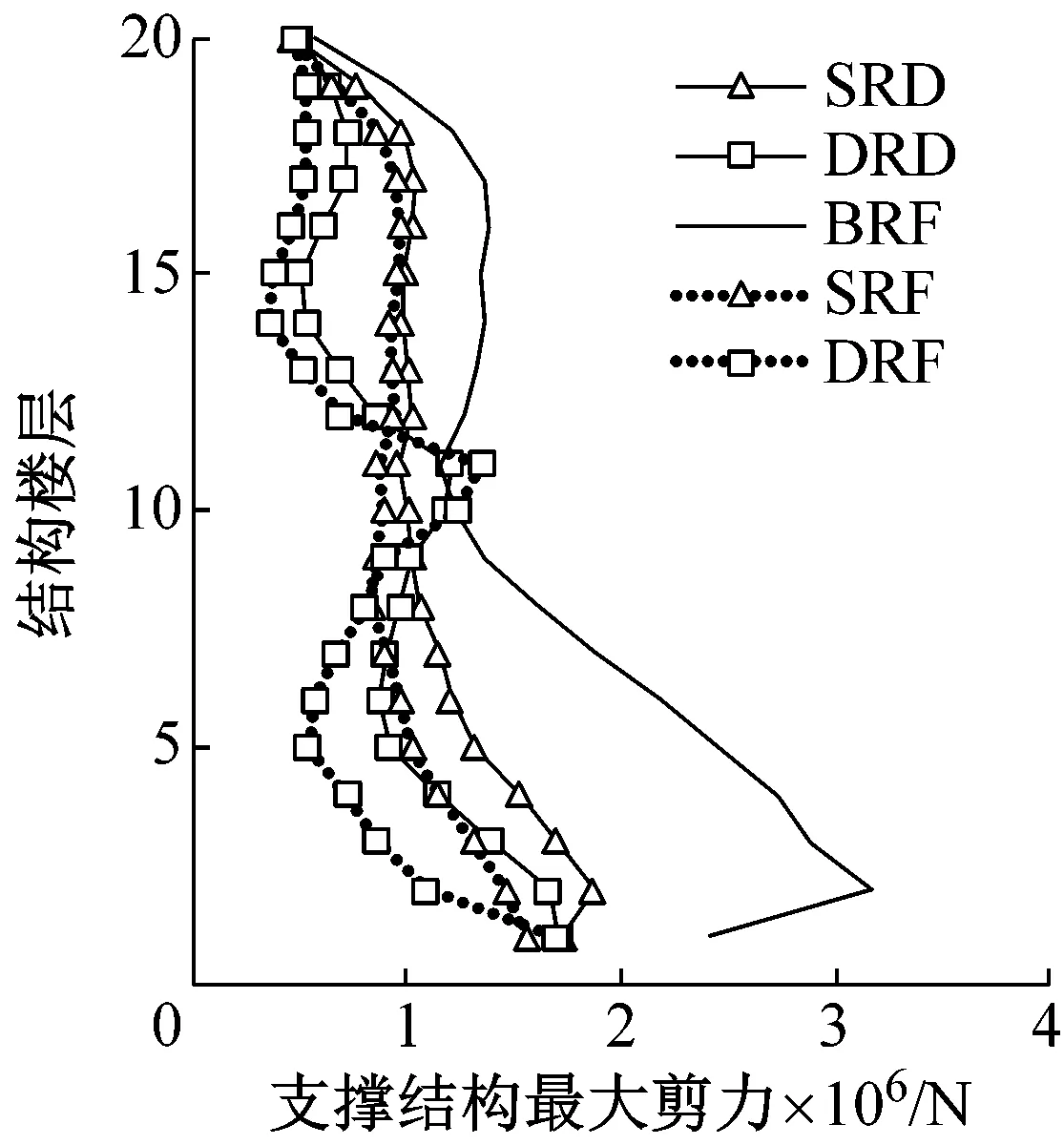
(d) 支撑结构最大剪力对比(e) 钢桁架弦杆最大轴力对比图8 不同结构的地震响应Fig.8 Dynamic response of analysis structures

(1) 摇摆钢桁架能够提高主体结构的抗震性能。相比于BRF结构，SRF结构最大层间位移角减小了31.3%，所承担的地震作用显著减小(楼层剪力减小54.8%，支撑构件轴力减小58.3%，摇摆钢桁架弦杆的轴力降低86.4%)。由于结构刚度和承载力较低，SRF结构的残余变形大于BRF结构，但是仍然满足1/200的建议限值[17]，且SRF结构各楼层的残余变形分布较均匀。

(2) BRC保障了摇摆结构的抗侧刚度与承载力，可以提升整体结构的抗震性能与可恢复性能。一方面，相比于SRF结构，SRD结构的最大层间位移角降低25.6%，残余层间位移角降低34.8%；另一方面，相比DRD结构，虽然DRF结构所承受的地震作用进一步降低，各楼层变形更均匀，但是其最大层间位移角增加41.9%，残余层间位移角增大59.8%，中间分段楼层支撑杆件的轴力增加了10.8%。因此，消能摇摆结构体系(双段体系和单段体系)必须配置位移型阻尼器，以保障体系的抗侧刚度与承载力。

(3) 双段消能摇摆结构体系的地震响应较单段消能摇摆结构体系进一步降低。相比于SRD结构，DRD结构的最大层间位移角减小了23.2%，残余层间位移角降低41.7%，摇摆结构的内力水平显著下降(楼层最大剪力减小38.0%，摇摆桁架弦杆的最大轴力降低68.8%，支撑构件的最大轴力降低49.2%)，抗震性能与可恢复性能更为优越。同时，双段摇摆机制抑制了高阶振型的影响，可以控制主体结构变形更均匀，摇摆结构的构件内力沿高度分布亦更均匀。

(4) 相比于传统支撑框架结构，双段消能摇摆结构体系的抗震性能与可恢复性能更加优越。罕遇地震作用下，DRD结构的动力响应较BRF结构显著减小：最大层间位移角减小37.5%，上部楼层残余层间位移角减小44.1%，最大楼层剪力下降58.8%，支撑杆件最大轴力下降62.7%，摇摆钢桁架弦杆最大轴力下降76.5%。

3.3 结构弹塑性地震反应的不均匀性

为描述结构变形的不均匀程度，采用文献[18]推荐的无量纲指标：层间位移集中系数FDC(drift concentration factor，DCF)，按式(1)进行计算。

(1)

式中:[Δ]为层间位移角向量;H为结构总高度;Δi为第i层层间位移角;hi为第i层层高。

表5 结构层间变形集中系数DCF

结构平均DCF值如表5所示，可知：

(1) 摇摆结构可以控制主体结构各楼层变形更加均匀。BRF结构DCF最大，各楼层变形最不均匀。

(2) 相比于单段摇摆结构，双段摇摆结构可以控制主体结构对应各楼层的变形更均匀。DRD结构的DCF小于SRD结构，其各楼层变形更加均匀；DRF结构的DCF小于SRF结构，其各楼层变形亦更均匀。

(3) BRC对摇摆结构存在反力，会加剧主体结构变形的不均匀性。SRF结构的DCF小于SRD结构，其各楼层变形更均匀；DRF结构的DCF小于DRD结构，其各楼层变形亦更加均匀。

3.4 结构损伤分布

为描述结构的塑性损伤分布，根据式(2)的原理编制了OpenSees软件的后处理程序，用以计算各类构件累积塑性耗能占地震输入总能量的比例。式中，γi表示第i类构件的累积塑性耗能占比，i可表示框架梁、框架柱等构件；Epi表示第i类构件的累积塑性耗能；Ein表示地震动输入总能量；Fij(t)表示i类构件的第j个单元在全局坐标系下节点力时程函数；Δij(t)表示i类构件的第j个单元在全局坐标系下节点位移时程函数；mj表示第j个集中质量；ug(t)表示一致激励下的地震动加速度时程函数；xj(t)表示第j个集中质量的位移时程函数。

(2)

图9给出了BRF结构、SRD结构、DRD结构、SRF结构和DRF结构框架梁累积塑性耗能占地震输入能量的比例，图10给出了不同构件的累积塑性耗能占地震输入能量的比例，表6给出了框架柱累积塑性耗能占地震输入能量的比例。

图9 框架梁累积塑性耗能占比Fig.9 Energy dissipation ratio of frame beams

图10 不同构件累积塑性耗能占比Fig.10 Energy dissipation ratio of different components

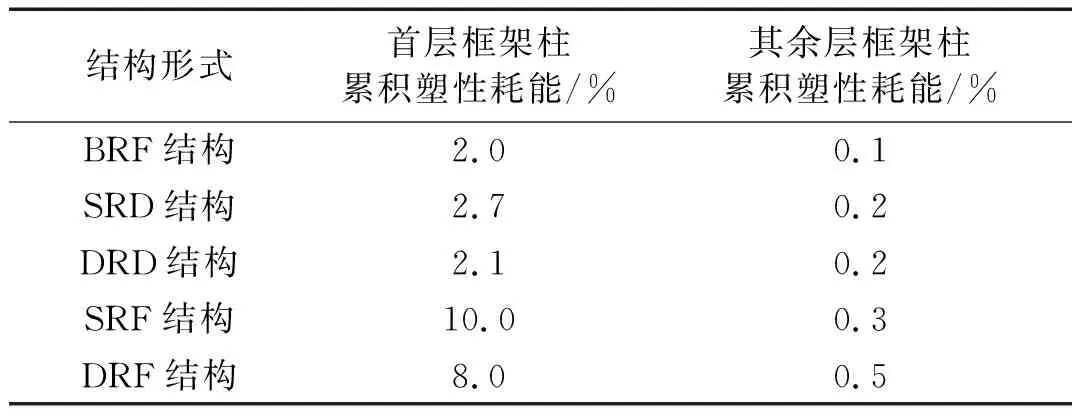
表6 框架柱累积塑性耗能占比

由表6可知：

(1) 框架结构的累积塑性耗能集中于框架梁，呈“强柱弱梁”的损伤机制，原型结构设计合理。

(2) SRD结构与DRD结构主体框架的累积塑性耗能小于BRF结构，结构塑性耗能集中于阻尼器，消能摇摆结构体系的抗震性能良好。双段摇摆机制相比于单段摇摆机制，主体框架的塑性损伤更小、BRC耗能更充分，结构抗震性能更加优越。

(3) 由于DRF结构和SRF结构的刚度和承载力小于BRF结构，两者主体结构在地震作用下的塑性损伤高于BRF结构。DRF结构的抗震性能优于SRF结构，其框架结构累积塑性损伤小于SRF结构。

(4) BRF结构塑性损伤集中于上部楼层的框架梁，SRD结构、DRD结构的塑性损伤沿结构高度分布较均匀，可见摇摆钢桁架能够控制结构各楼层均匀变形，有助于遏制薄弱层的产生。

(5 )SRD结构、DRD结构、SRF结构和DRF结构框架柱的塑性损伤集中于首层，其余楼层框架柱基本保持弹性。摇摆钢桁架对于首层框架柱存在附加约束，首层框架柱的塑性损伤较BRF结构更严重。

4 结构易损性评估

为评估不同结构体系的抗倒塌性能，分别对BRF结构、SRD结构、DRD结构、SRF结构和DRF结构进行增量动力时程分析(incremental dynamic analysis，IDA)。本文选用ATC-63推荐的50条地震动记录作为输入激励，其加速度反应谱信息如图11所示。

4.1 计算指标

本文选取PGA作为地震动强度指标(intensitymeasure，IM)，以100 gal作为调幅增量，取至2 000 gal，共计20种取值；选用结构最大层间位移角作为工程需求参数(engineering demand parameter，EDP)。根据《建筑抗震设计规范》，钢结构的抗震性能水准可以划分为：基本完好(P1)、轻微损坏(P2)、中等破坏(P3)以及不严重破坏(P4)四类，对应的层间位移角限值为：1/300、1/200、1/100和1/55，以此作为结构四种性能水准的划分标准。

图11 用于IDA的地震动加速度反应谱Fig.11 Acceleration response spectrum of waves for IDA

根据文献[19]，可假设结构在指定IM下的EDP服从对数正态分布。当IM为c时，结构EDP对性能水准Pi(i=1,2,3,4)的超越概率Pfi|(IM=c)可按式(3)计算，式中λ表示IM为c时结构的倒塌比例，Φ表示标准正态分布的累积概率函数，μln(EDP)|(IM=c)表示IM为c时ln(EDP)的均值，σln(EDP)|(IM=c)表示IM为c时ln(EDP)的标准差。当IM遍历IDA过程中所有的PGA取值，对应Pfi连接所得的曲线即为该结构对于性能水准Pi的易损性曲线。

(3)

4.2 易损性分析

假定BRF结构、SRD结构、DRD结构、SRF结构和DRF结构对四种性能水准的易损性曲线服从累积正态概率分布函数，经光滑处理后如图12所示。各条易损性曲线的特征参数如表7所示，特征参数包括均值μ与抗倒塌储备系数(collapse margin ratio,CMR)。

均值表示结构对指定性能水准的超越概率达到50%时所对应的IM指标，反映了结构平均抗倒塌能力，均值越高，结构抗倒塌能力越强。

抗倒塌储备系数表示结构对某性能水准超越概率为50%时的IM指标与罕遇地震所对应IM指标的比值，即均值μ与400 gal的比值，CMR越高，结构抗倒塌能力越强。计算CMR时为保证选取的性能水准与规范[12]罕遇地震对应的IM指标一致，以1/50的层间位移角限值作为性能水准P0，获得不同结构对于P0的易损性曲线，从而得到相应的CMR1/50,IM=400。

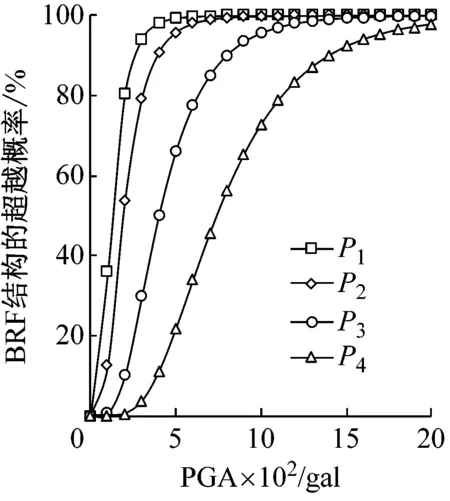
(a) BRF结构的易损性曲线(b) SRD结构的易损性曲线(c) DRD结构的易损性曲线

(d) SRF结构的易损性曲线(e) DRF结构的易损性曲线图12 不同结构对四种性能水准的易损性曲线Fig.12 Fragility curves of analysis structures to four limited states

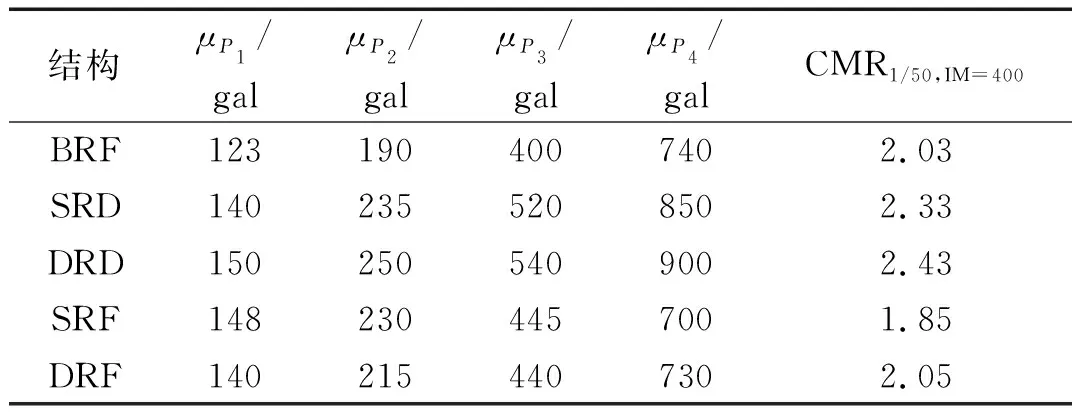
表7 不同结构易损性曲线的特征参数

分别提取IM为70 gal(多遇地震)、200 gal(设防地震)、400 gal(罕遇地震)、620 gal(极罕遇地震)时，各分析结构对于四种性能水准(P1～P4)的超越概率，可得易损性矩阵，如表8所示。

由表8可知：

(1) 在不同地震作用下，DRD结构对于各性能水准的超越概率均小于SRD结构，易损性曲线的均值μ大于SRD结构，抗倒塌储备系数值CMR更大，双段消能摇摆结构体系的抗震性能与抗倒塌性能比单段消能摇摆结构体系更优越。

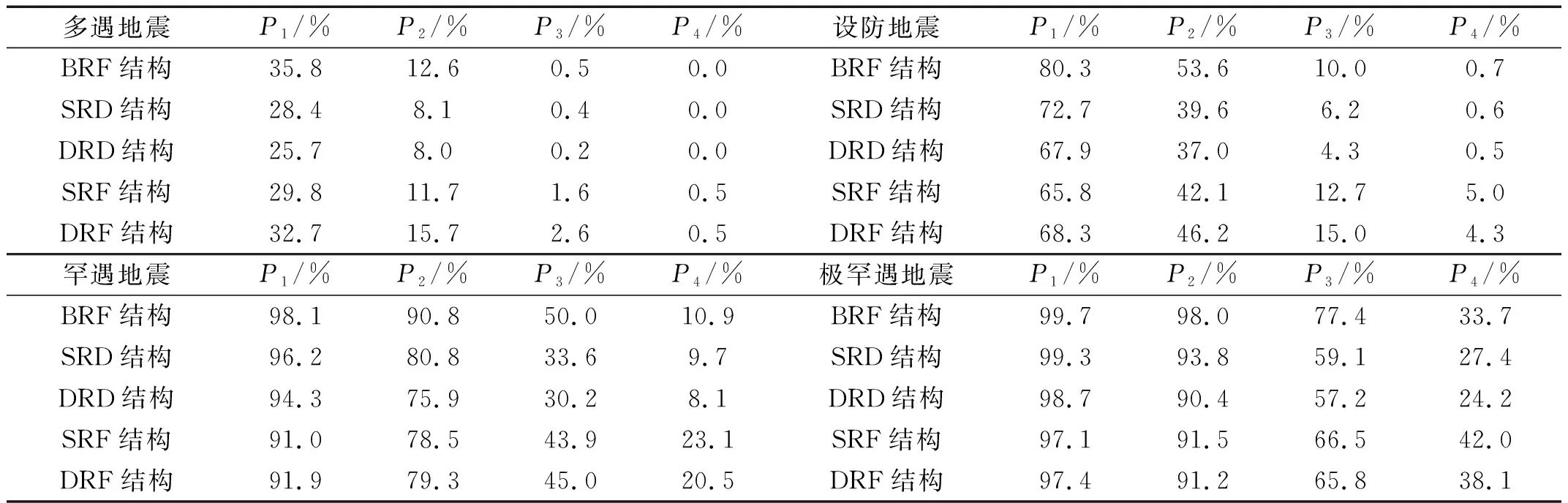
表8 不同结构的易损性矩阵

(2) 在不同地震作用下，BRF结构对于各性能水准的超越概率均大于SRD结构和DRD结构，易损性曲线的均值μ低于SRD结构，CMR更低，其抗震性能与抗倒塌性能不如SRD结构和DRD结构。

(3) 在不同地震作用下，DRF结构对性能水准P4(不严重破坏)的超越概率大于BRF结构，SRF结构对性能水准P4(不严重破坏)的超越概率大于DRF结构。摇摆结构虽然可以控制主体结构各楼层均匀变形，遏制薄弱层产生，但因其刚度和承载力较弱(缺少BRC)，SRF结构与DRF结构的抗倒塌性能不如BRF结构。此外，双段摇摆结构体系较单段摇摆结构体系抗倒塌性能更优越。

(4) 从抗倒塌储备系数来看：含有BRC的消能摇摆结构体系抗倒塌能力优于传统支撑框架结构，且双段消能摇摆结构体系的抗倒塌性能优于单段消能摇摆结构体系；不含BRC的摇摆结构体系因刚度和承载力较低，抗倒塌能力不如传统支撑框架结构，双段摇摆结构体系的抗倒塌性能优于单段摇摆结构体系。

5 结 论

单段消能摇摆结构体系较难应用于高层建筑，摇摆结构的设计需求受高阶振型影响较大。本文提出了双段消能摇摆结构体系。通过对几种不同结构进行静力弹塑性分析、动力弹塑性时程分析以及增量动力时程分析，评估了双段消能摇摆结构体系的抗震性能、可恢复性能与抗倒塌性能，得出以下结论：

(1) 相比于传统支撑框架结构体系，双段消能摇摆结构体系的抗侧刚度与承载力有所下降，但是其在罕遇地震作用下的动力响应和残余变形显著减小(最大层间位移角减小33.9%，残余层间位移角减小44.1%)，摇摆结构的内力水平更低(支撑杆件最大轴力下降62.7%)，结构累积塑性损伤程度更低(框架结构累积塑性耗能占比减小51.4%)，主体结构各楼层变形更加均匀(层间变形不均匀系数DCF减小15.6%)，抗倒塌性能更优越(抗倒塌储备系数CMR增加16.5%)。

(2) 相比于单段消能摇摆结构体系，双段消能摇摆结构体系的抗侧刚度和承载力与之相当，罕遇地震反应显著减小(最大层间位移角减小21.5%，楼层最大剪力减小32.9%)，残余层间位移角减小57.3%，摇摆结构内力更小(支撑杆件最大轴力下降65.3%)，各分段主体结构的楼层变形更均匀(层间变形不均匀系数DCF减小6.8%)，结构塑性损伤程度更低(框架结构累积塑性耗能占比减小29.0%)，抗倒塌性能更优越(抗倒塌储备系数CMR增加4.3%)。与单段摇摆机制相比，双段摇摆机制可以提高结构的抗震性能、可恢复性能与抗倒塌性能，抑制高阶振型的影响，降低摇摆结构的设计需求，可应用于更高的建筑。

(3) 相比于不含BRC的双段摇摆结构体系，包含BRC的双段消能摇摆结构体系具有更高的抗侧刚度和承载力，其地震反应显著降低(最大层间位移角减小41.9%)，震后残余变形更小(残余层间位移角减小59.8%)，主体结构的塑性损伤程度更低(框架结构累积塑性耗能占比减小67.7%)，抗倒塌性能更优越(抗倒塌储备系数CMR增加15.6%)。