钢框架结构在坠落块体撞击作用下的动力效应分析

乔惠云，罗才松，马永超，陈 誉

(1．福建工程学院 土木工程学院，福州 350118；2．福建省土木工程新技术与信息化重点实验室，福州 350118；3．福州大学 土木工程学院，福州 350116)

连续性倒塌是指初始局部构件破坏向其它构件扩展，最终导致结构整体破坏或者大范围区域的倒塌。一般来说，局部构件失效主要影响正上方的剩余结构，其传力路径与构件失效前相比发生较大变化，表现出不同的抗倒塌机制，比如悬链线效应、压拱效应和空腹效应。Yang等[1-2]通过静力加载试验研究梁柱子结构在中柱失效下从弯曲效应向悬链线效应发展情况。周育泷等[3]建立了梁板子结构在压拱效应下的抗连续倒塌分析模型。钱凯等[4]研究边柱失效下梁-板子结构依靠压拱机制抵抗倒塌的机理。Qiao等[5-6]采用顶层子结构模型估算了空腹效应贡献。

需要注意的是，局部构件失效引起局部块体撞击下层构件，甚至局部构件掉落冲击下层结构的情况。如果下层结构的撞击承载能力小于撞击荷载甚至发生局部倒塌，会改变上层结构的边界条件，阻碍上层结构通过抗倒塌机制传递不平衡荷载，整个框架可能会发生连续倒塌。结构撞击问题由于其高度非线性，对应的研究较少。程小卫等[7]、邹淼等[8]、崔娟玲等[9]和王银等[10]分别通过试验和有限元方式研究了各种柱结构在侧向撞击作用下的动力性能。韩大伟等[11]研究矩形薄板在面内撞击荷载下动力屈曲性能。还有一些研究关于梁结构的撞击行为，Vlassis等[12]分析上层梁撞击下层梁的动力反应，吴波等[13]分析上层楼板撞击下层楼板的抗倒塌机制。Fujikake等[14]对一组混凝土梁进行落锤冲击试验，霍静思等[15]进行了一系列落锤冲击钢梁或节点的试验，研究梁或节点的抗冲击力学性能。Wang等[16]对梁在冲击荷载下的动力性能进行参数研究，建议用能量来估计钢梁在冲击荷载下的动力特性。还有学者采用拟静力方法分析动力撞击问题，并提出合适的动力放大因子[17-19]。

下层结构能够抵抗撞击荷载，是多层框架抵抗连续倒塌研究的重要组成部分。本文研究框架梁在撞击荷载下的动力反应，主要考虑完全塑性撞击和完全刚性撞击两种极端情况，根据撞击理论分析和数值分析，并结合梁的变形能函数，估算被撞击梁最大位移的上限值和下限值。

1 钢梁承受撞击的理论分析

框架结构受到坠落块体的撞击，与撞击点的位置和撞击力的大小有关。将坠落块体视为刚体，通过动量守恒和能量守恒定律来获得撞击力的大小。根据撞击过程有无较大的能量损失，将撞击过程分为完全塑性撞击和完全刚性撞击。撞击过程是一个复杂的动力过程，介于完全塑性和刚性撞击之间。

1.1 完全塑性撞击

(1)

完全塑性撞击使块体和被撞梁合为一个整体，假设梁呈现三角形刚塑性破坏机制，其速度场如图1所示，三角形顶点的速度为vm1。由于块体和框架梁的撞击力很大，两者组成系统的内力远大于系统受到的外力，近似认为系统的角动量守恒。

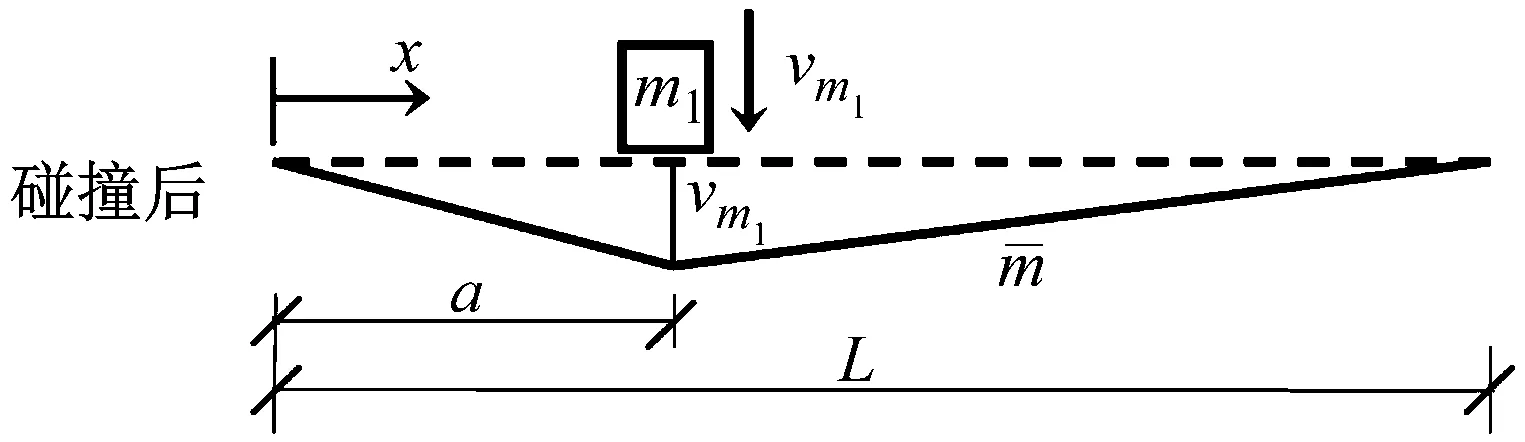
图1 完全塑性碰撞前后梁的速度场分布

(2)

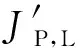
(3)

(4)

(5)

整理式(2)得到完全塑性撞击后梁在撞击点的速度vm1为

(6)

若撞击点位于梁跨中(a=0.5L)，式(6)可简化为

(7)

1.2 完全刚性撞击

完全刚性撞击使块体和被撞击梁在撞击结束后独立运动。块体的反弹速度为v2，被撞击梁呈现刚塑性破坏机制，速度场呈三角形分布，如图2所示，框架梁撞击中心的速度为vm2。

按照与完全塑性撞击分析类似方法，将撞击系统以撞击点为界限分为两部分，刚性撞击系统在碰撞前和碰撞后的角动量守恒关系为

(8)

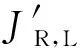
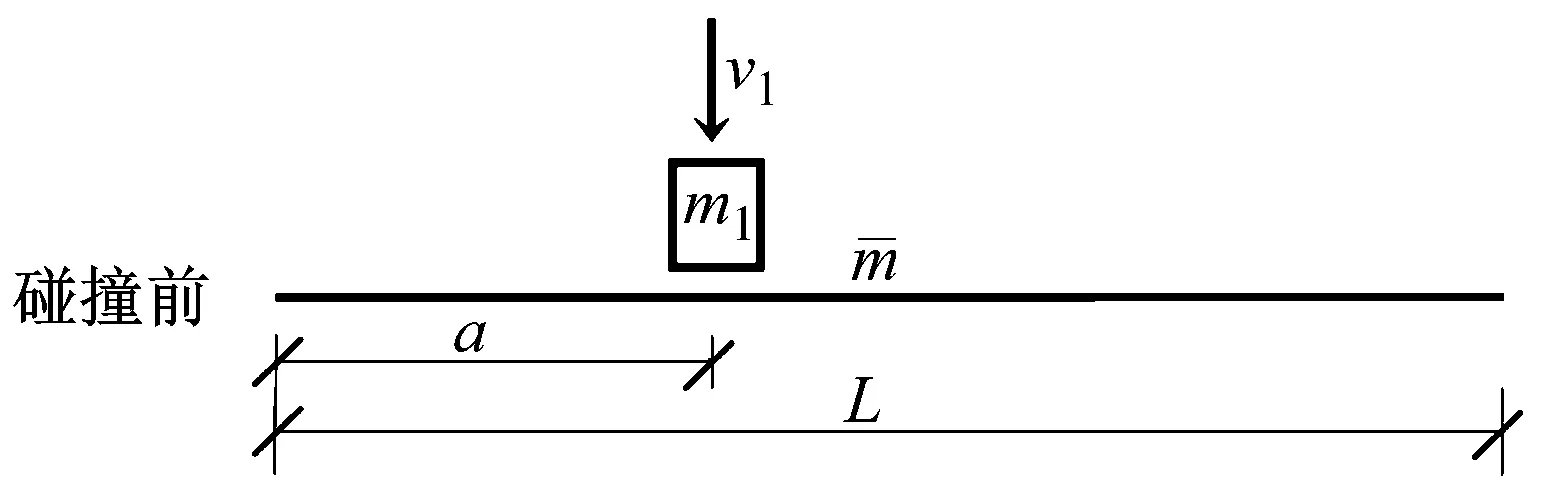
图2 完全刚性碰撞前后梁的速度场分布

和右侧分别对梁A端和B端的角动量，可由式(9)、(10)和(11)分别表示为

(9)

(10)

(11)

整理角动量平衡等式(8)，得到完全刚性撞击后梁的速度vm2由块体反弹速度v2表示为

(12)

完全刚性撞击的能量损失可以忽略不计，满足能量守恒定律，块体撞击力对被撞梁做功WE等于被撞梁的能量变化，包括梁的动能EK，结构阻尼能量耗散ED，结构变形能量EA，被撞梁的能量变化表示为

EK+ED+EA=WE

(13)

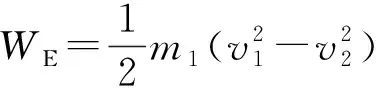
(14)

对式(14)左侧积分运算，并整理得到

(15)

完全刚性撞击后可能发生多次反弹，有多次能量传递，实际撞击过程结束时，被撞击梁获得的动能相对较高，为了简化只考虑第一次撞击和反弹引起的能量传递。依据式(12)动量守恒和式(15)能量守恒定律，计算得到撞击后梁的速度vm2为

(16)

若撞击点位于梁跨中，即a=0.5L，且撞击块体的质量远小于被撞击梁的总质量，式(16)可简化为

(17)

1.3 理论模型验证

图3 有限元模型Fig.3 The finite element model

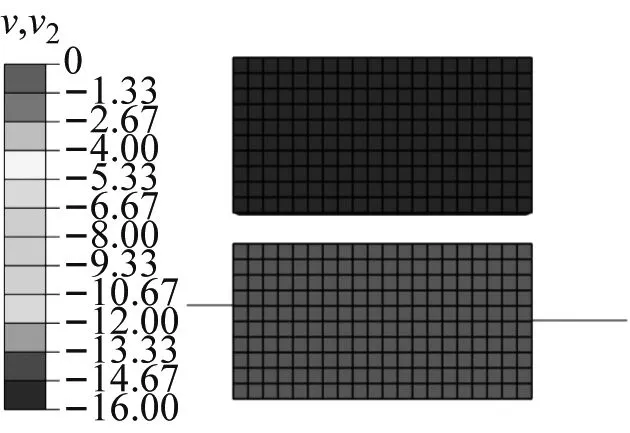
(a) 碰撞前vm=0(b) 碰撞中vm=vm，max(c) 碰撞后图4 撞击过程速度云图Fig.4 Velocity nephogram of impact process

在基本模型的基础上，改变坠块的速度v1和质量m1等参数，计算撞击后钢梁的速度vm，并和完全刚性和塑性理论模型对比，如图5所示。

2 评估撞击后梁的位移

碰撞问题是一个高度非线性问题，梁被撞击以后的动力特性对研究其受力至关重要，其中最大位移是一个关键动力特性。完全塑性撞击和完全刚性撞击是两种极端情况，可以确定梁在块体撞击后最大位移的上限值和下限值。

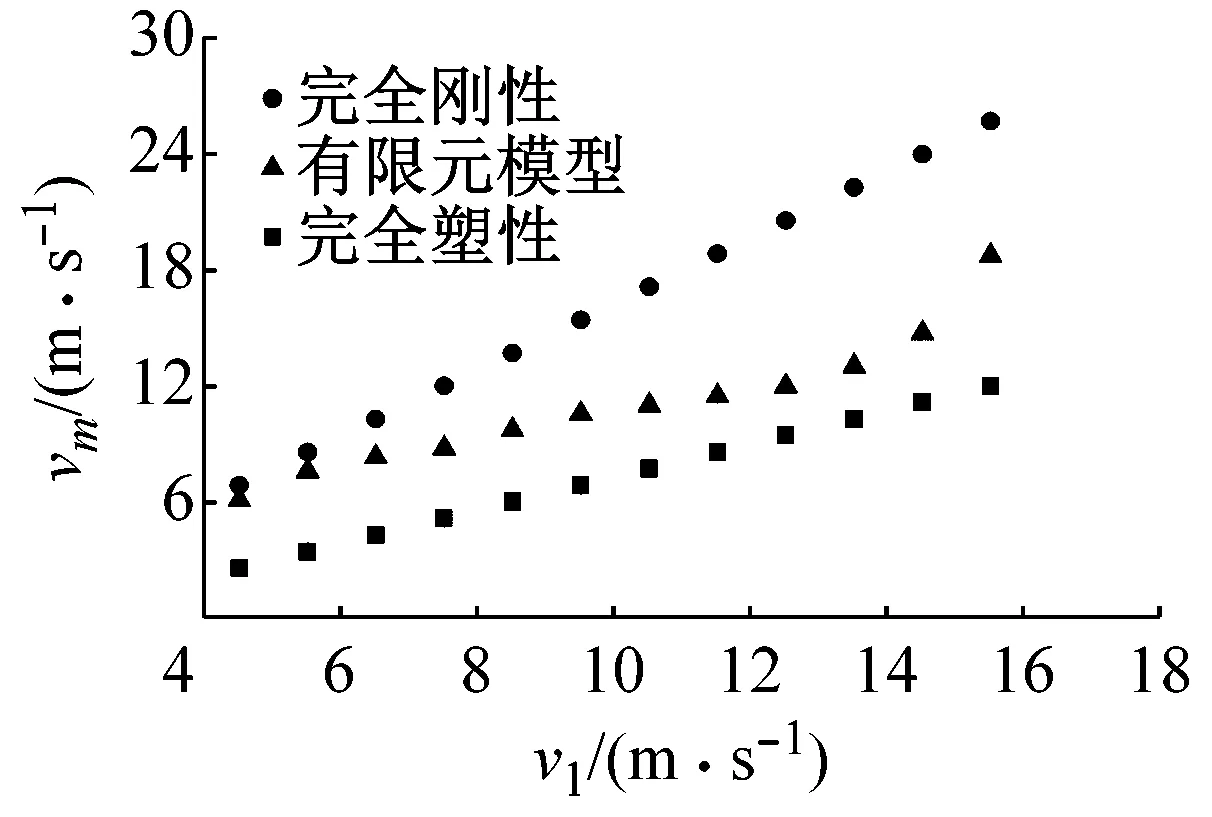
(a) 坠块速度v1的影响(b) 坠块质量m1的影响(c) 坠块落点位置a/L的影响

(18)

完全刚性撞击后，梁的动能Ek由vm2表示为

(19)

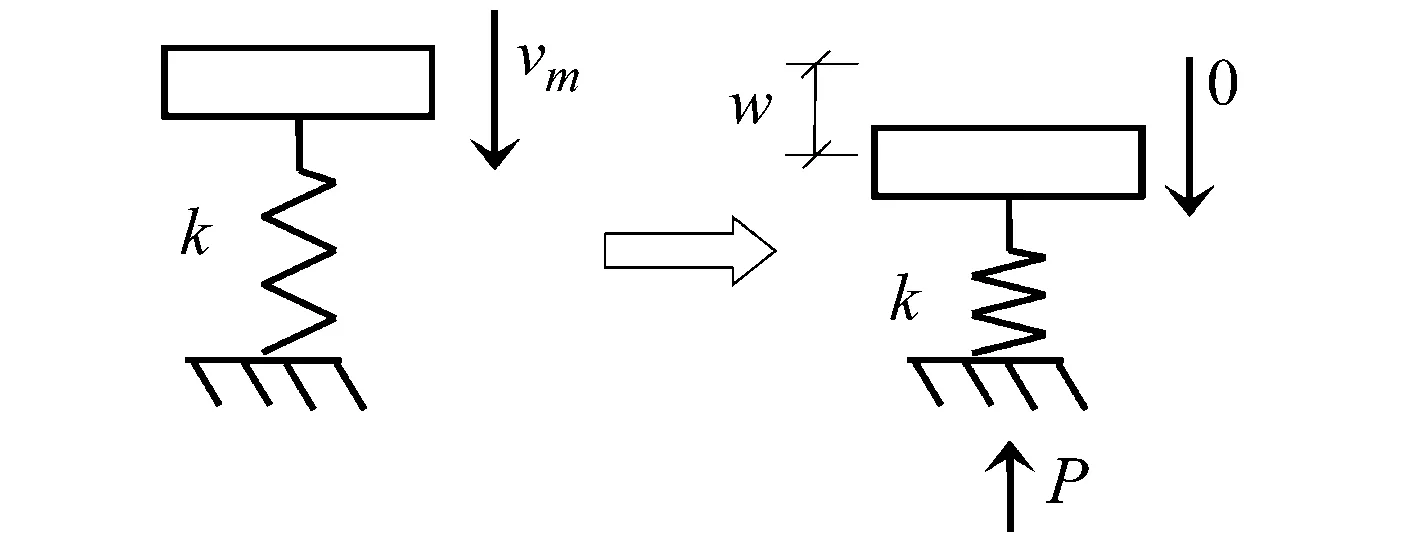
(a) 能量转化系统

(b) 柱的抗力-位移关系图6 动能转化为变形能Fig.6 Conversion of kinetic energy into deformation energy

在图6(a)中，碰撞系统中梁的刚度k不是一个定值，随梁位移w变化而变化。刚度k可由Izzuddin[20]推导的抗力-位移关系来表达，如图6(b)所示，抗力P随位移w先后经历四个阶段：弹性阶段、塑性阶段、悬链线过渡阶段和悬链线阶段。当撞击后梁的速度从vm降低到零，撞击点达到其最大竖向位移时，认为动能Ek全部转化为梁的变形能R(w)。梁的变形能R(w)大小等于图6(b)曲线下包围的面积。乔惠云等[21]采用双跨梁子结构模型计算梁的变形能R(w)，将其应用到撞击梁，如式(20)所示

(20)

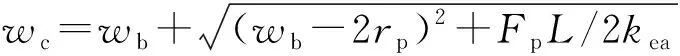
根据式(20)变形能R(w)函数和能量守恒定律，估算框架梁被撞击后的最大位移，步骤如图7所示。框架梁受坠落块体撞击后的最大位移，除了与块体的速度、质量、撞击点位置有关，还与框架梁自身的刚度和变形耗能情况有关。

3 撞击有限元模型

3.1 建立模型

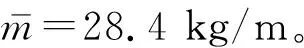
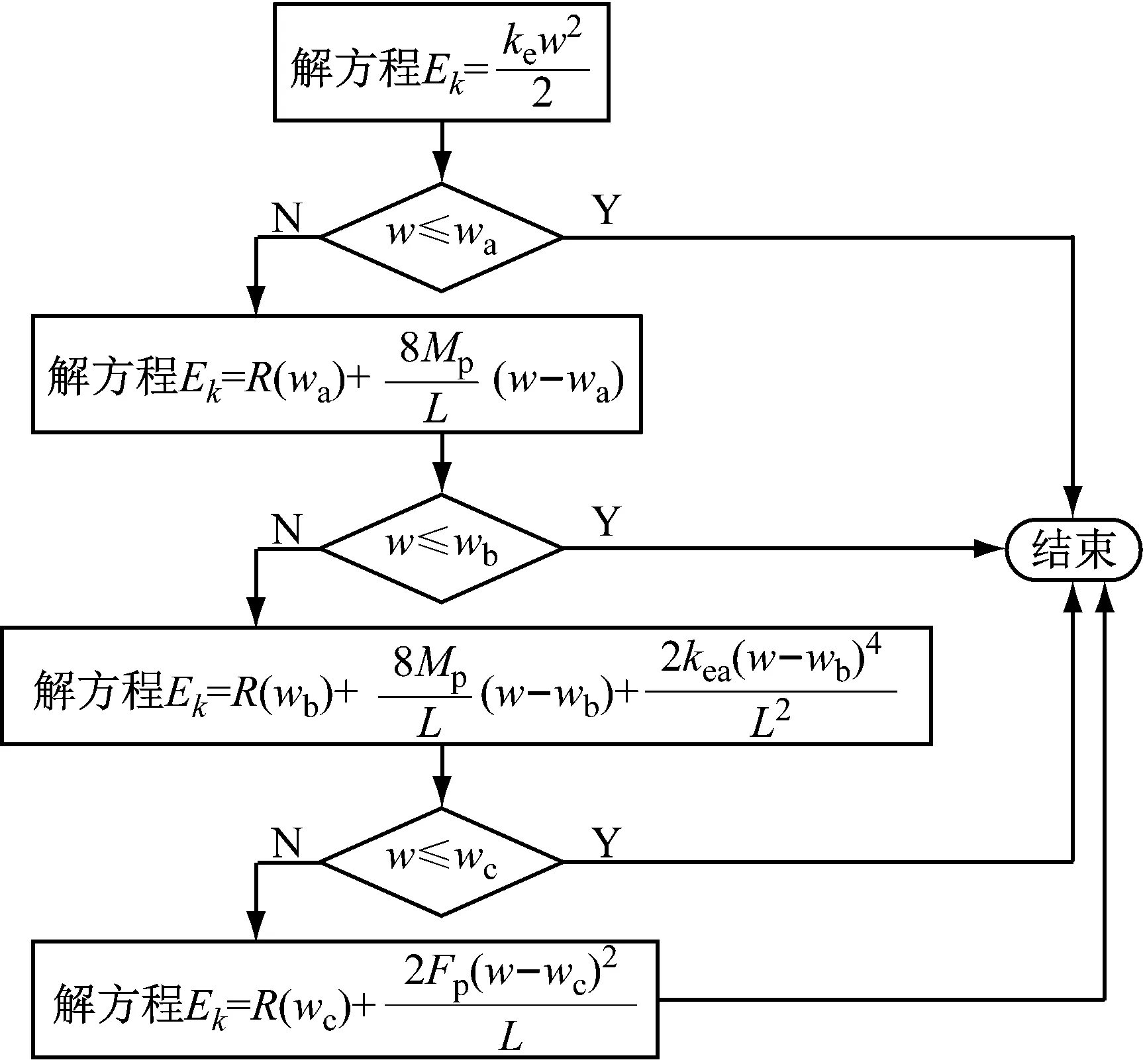
图7 最大位移计算步骤Fig.7 Steps of maximum displacement calculation

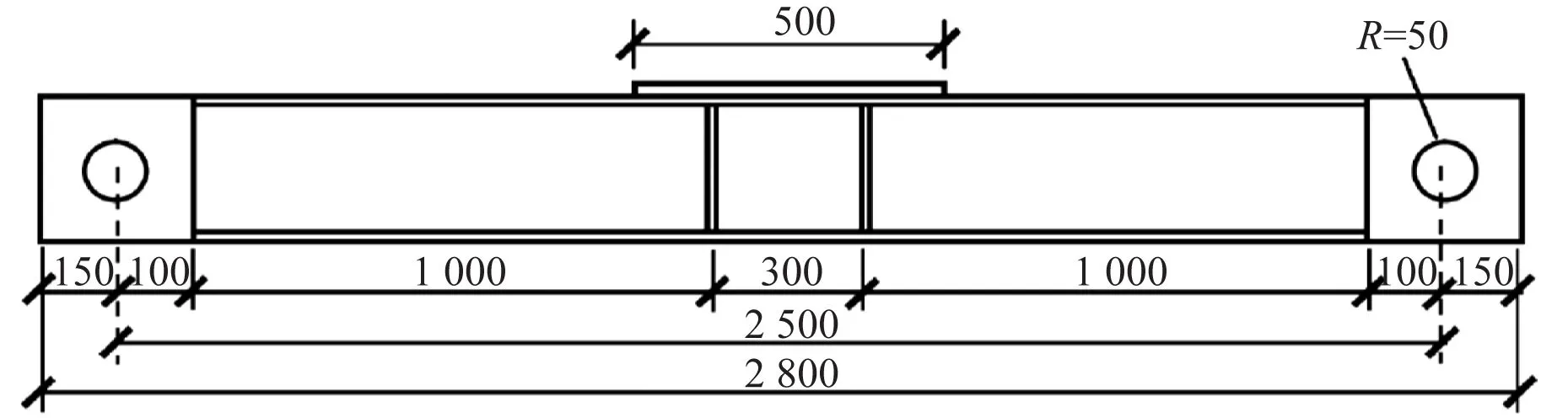
图8 钢梁尺寸示意图Fig.8 Schematic diagram of steel beam size

表1 试件的基本参数

采用ABAQUS软件建立钢梁试件的精细化有限元模型。被撞击梁和落锤均选用能克服“剪切自锁”和“沙漏”问题的8节点减缩积分单元(C3D8R)。落锤采用直径为200 mm、高度为200 mm的圆柱体，初始速度由预定义场施加，改变落锤的密度实现落锤重量变化。

为保证计算精度又兼顾计算效率，钢梁的撞击点和两端约束位置需加密网格，网格尺寸为10 mm，其它区域的网格尺寸为20 mm。落锤与钢梁的接触面采用通用接触，接触面的法向为“硬”接触，切向的摩擦因数为0.3。

碰撞等动态分析时材料受应变率影响很大，钢材的应变率采用Cowper-Symonds模型[22]，屈服应力与应变率的关系为

(21)

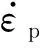
3.2 模型验证

落锤与钢梁之间的撞击力F时程曲线如图9所示，曲线包含峰值阶段、稳定阶段和衰减阶段，将模拟结果与试验结果对比，稳定阶段吻合较好；峰值阶段的模拟值与试验值差别较大，这是由于峰值荷载对接触方式更为敏感，模型采用的法向“硬”接触与实际撞击时刻接触面变形差别较大；衰减阶段模拟时间普遍比试验结果小，这是由于在有限元模拟的最后阶段重锤会反弹，而在试验过程中，为了避免重锤反弹跌落在试件以外区域，产生不安全因素，重锤的顶部连着钢撑杆，这种构造措施使得重锤只能下落，不能反弹，从而延长了碰撞时间。

钢梁撞击点的位移时程曲线如图10所示，将试件的模拟值与试验值对比，两者误差均小于5%。对比图9撞击力时程和图10位移时程曲线，发现撞击力处于峰值阶段时，钢梁位移值不大，而钢梁位移最大值发生在撞击力的稳定阶段。

撞击力时程曲线反映构件开始被撞击时有剧烈的动力特征，特别是撞击时间在t=0.3 ms以前，撞击力剧烈变化。取试件HR4-3应力云图为例说明，如图11所示。当t=0.05 ms时，钢梁与重锤边缘接触区域的应力为478 MPa，其它区域的应力几乎为0，钢梁最大位移为5×10-3mm；当t=0.15 ms时，钢梁与重锤边缘接触区域的应力向腹板发展，加劲肋逐步被包含在内，最大应力为541 MPa，钢梁最大位移为0.7 mm；当t=0.25 ms时，由于加劲肋的刚度大于腹板的刚度，应力沿着加劲肋向腹板和下翼缘发展，应力峰值出现在与加劲肋连接的下翼缘后，开始向支座方向传递，钢梁最大位移为2 mm；当t=16 ms时，撞击力已经达到稳定阶段，整根钢梁参与抵抗撞击力的作用，钢梁位移为60 mm，接近梁的最大位移60.8 mm。对比分析说明钢梁位移最大值发生在撞击力的稳定阶段。

4 理论分析验证

对块体撞击后的四个钢梁进一步分析，采用理论简化计算方法分析试件最大位移的上限值和下限值。根据完全塑性和完全刚性两种极端撞击确定速度等要素，并确定钢梁在两种极端情况下的动力特征。

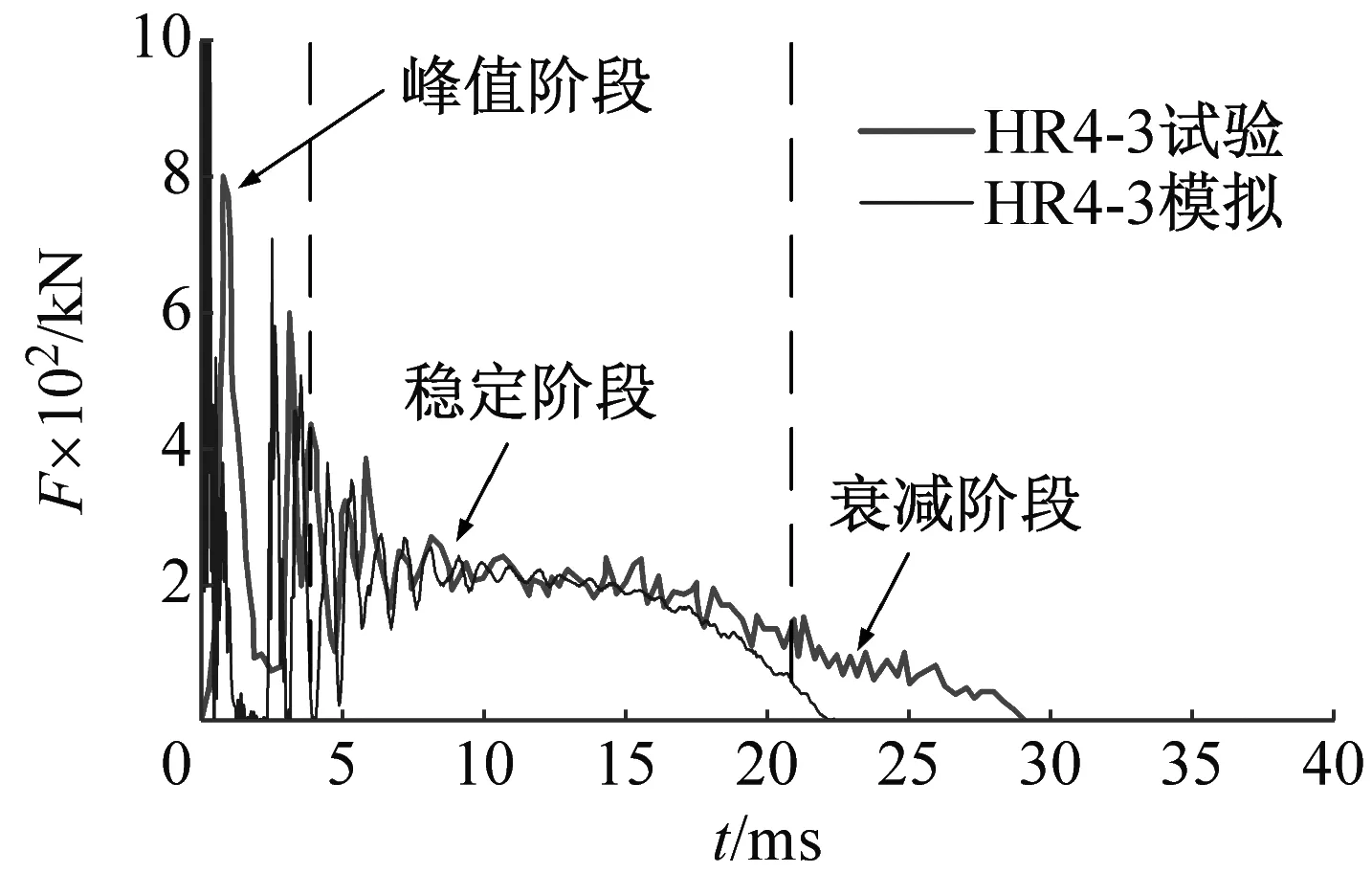
(a) HR4-3

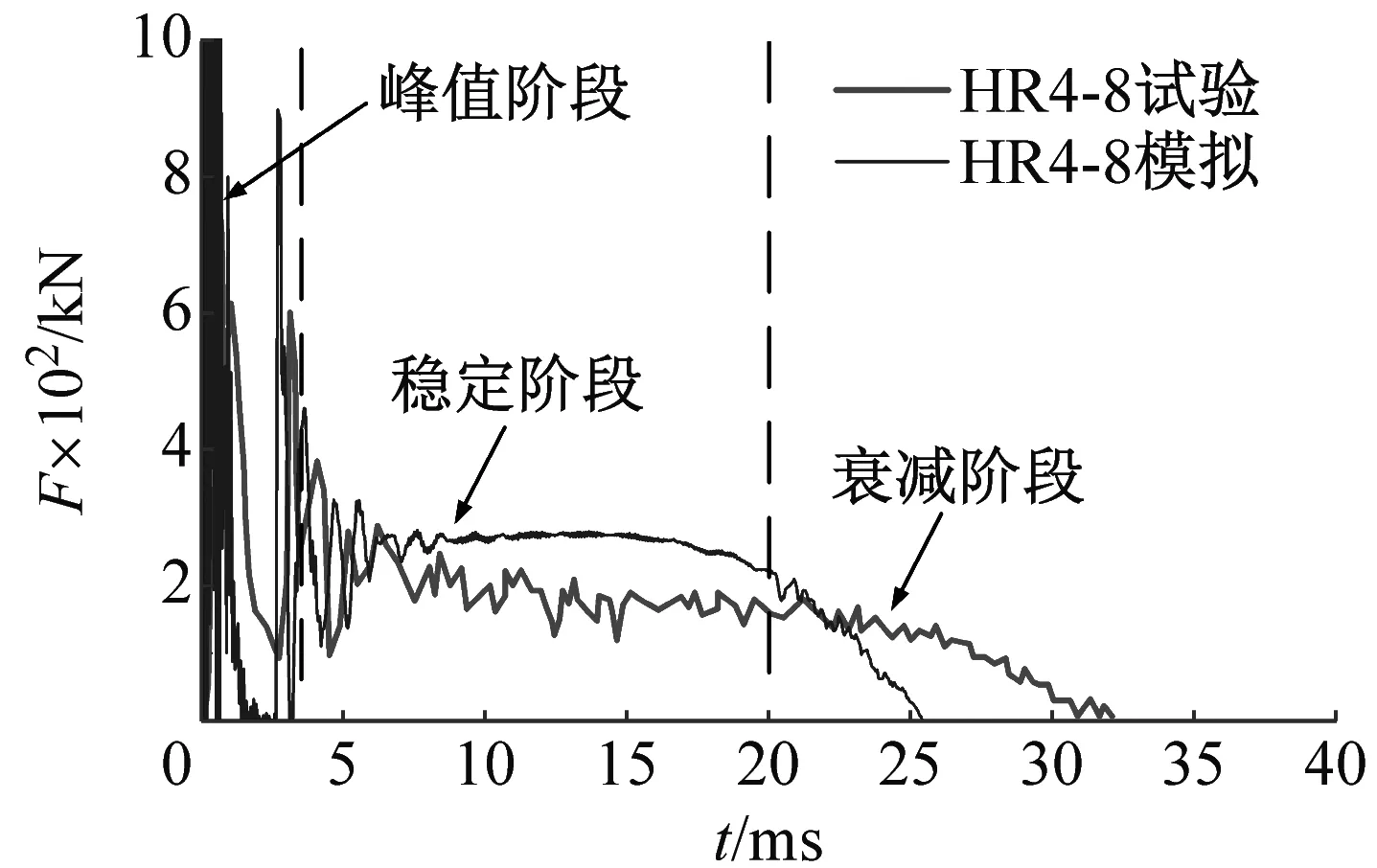
(c) HR4-8

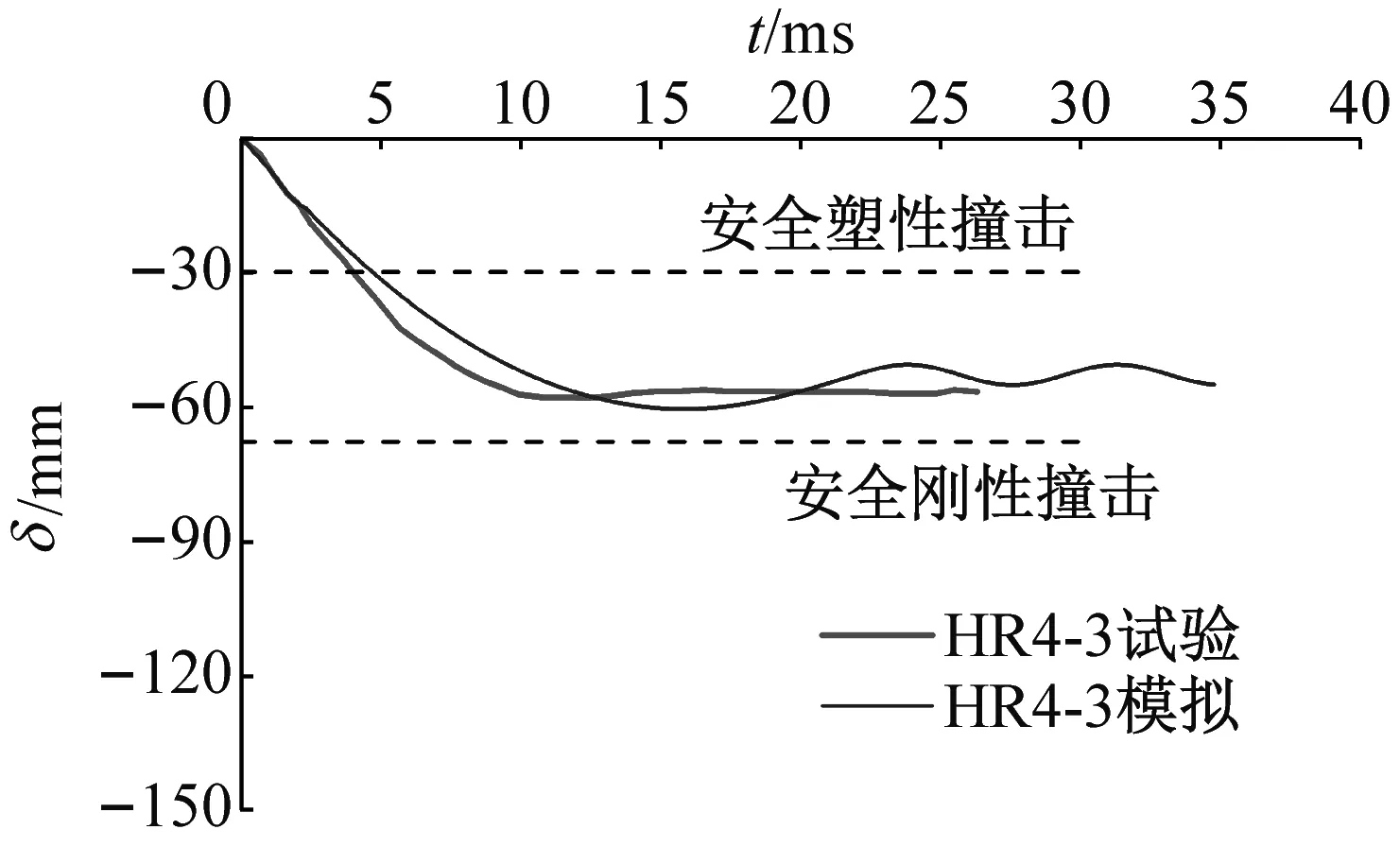
(a) HR4-3

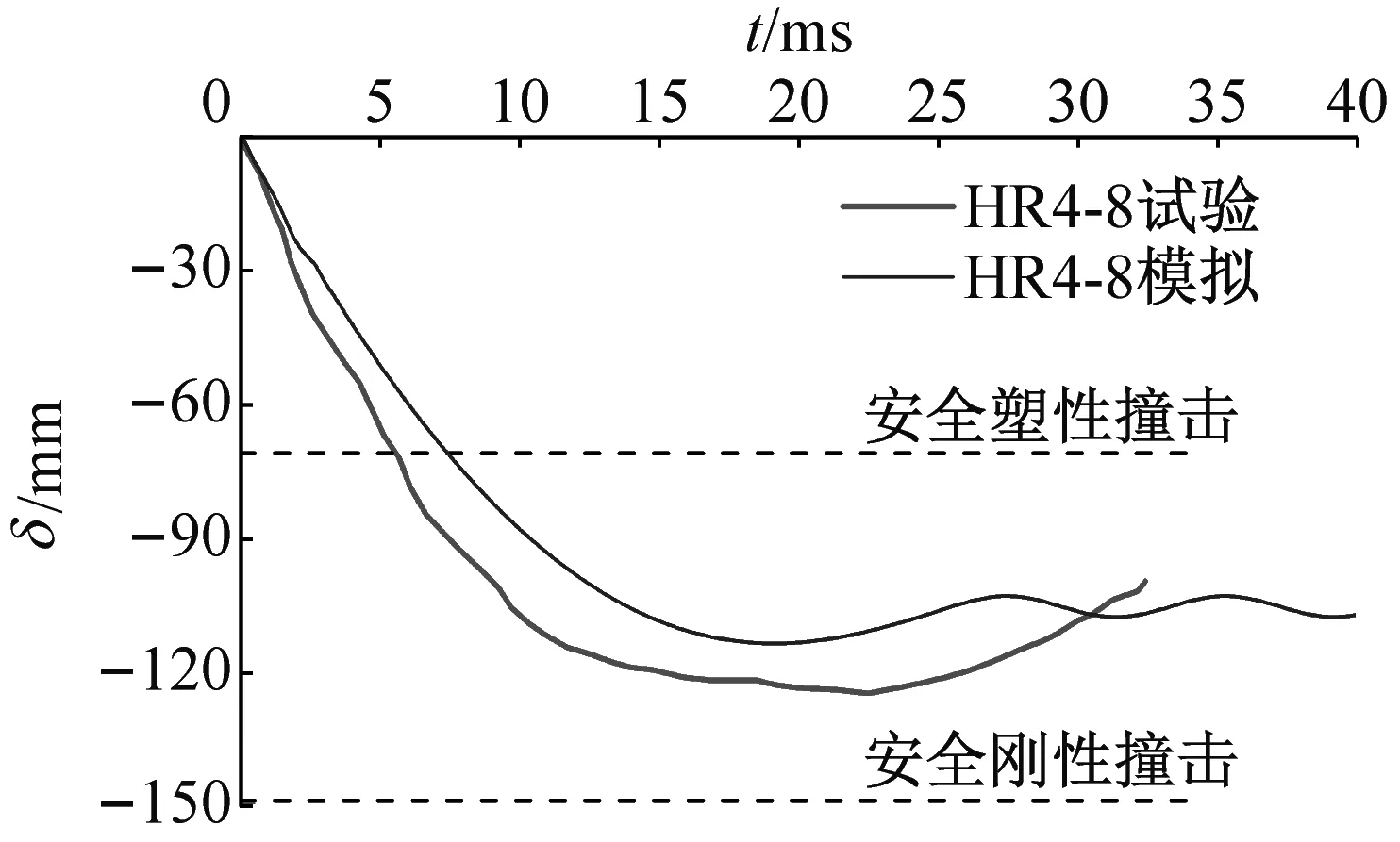
(c) HR4-8

(a) t=0.05 ms

(c) t=0.25 ms

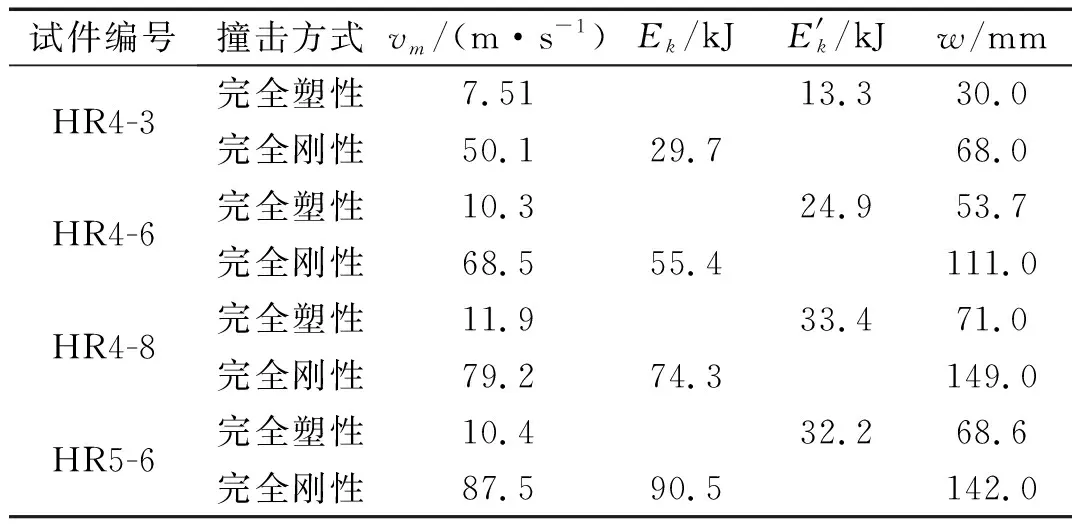
表2 理论分析结果

钢材的屈服强度在动力荷载作用下比较敏感，Malvar等[23]认为需要将钢材静力屈服强度乘以动力放大系数FDI(dynamic increase factor,DIF)，根据霍静思等的建议，动态屈服强度fyd=FDI·fy=1.73×251=434 MPa，弹性模量E=1.89×105MPa，钢材的密度采用7 800 kg/m3。由式(20)计算被撞击钢梁在不同阶段的变形能。将计算结果与试验结果和模拟结果对比，如图10所示，表明可以采用完全塑性和完全刚性两种极端碰撞情况初步估算碰撞后梁的最大位移，为实际坠落块体撞击框架梁的情况参考。

5 结 论

本文研究落层撞击引起框架结构的动力响应，考虑了两种极端情况：完全塑性撞击和完全刚性撞击，主要结论如下：

(1) 框架梁受块体撞击介于完全塑性撞击和完全刚性撞击之间，根据两种极端情况可以估算框架梁在块体撞击后最大位移的上限值和下限值。

(2) 构件开始被撞击时有剧烈的动力特征，撞击力处于峰值阶段时，框架梁的位移来不及发生变化，位移最大值发生在撞击力的稳定阶段。

(3) 坠落块体速度小时，与梁碰撞接近于完全刚性撞击，坠块速度较大时，与梁碰撞接近于完全塑性撞击。

(4) 坠块撞击点在跨中附近时，理论模型与有限元模型差别较小，撞击点位于约束端时，完全刚性理论计算值比模拟值偏大。