基于光滑粒子流方法的全断面岩石掘进机盘形滚刀侧向力研究

赵晓旭，贾春强，孙 佳，侯祥林

（沈阳建筑大学机械工程学院，辽宁沈阳110168）

目前，中国已成为世界上隧道盾构技术应用最多的国家，而全断面岩石掘进机（TBM）作为一种技术密集型成套装备，已经成为各种长大岩石隧道施工的首选。盘形滚刀是TBM的主要破岩工具，刀盘在推力和扭矩作用下使滚刀实现滚压破岩运动，这种运动是一种复杂的空间运动。在破岩过程中，盘形滚刀除了受到正压力和滚动力的作用，还会受到侧向力作用，甚至会出现侧向力大于滚动力的情况。盘形滚刀受力分析是确定TBM刀盘推力和扭矩的基础，但是由于没有一个普遍接受的模型，刀盘设计中很少考虑滚刀侧向受力因素。另外一些研究表明，侧向力有时同滚刀磨损、轴承损坏以及刀盘受力不均等问题关系密切，因此，侧向力研究对于延长滚刀寿命、优化刀盘布局以及改善TBM施工工艺等具有重要意义［1］。

盘形滚刀破岩的物理现象和力学特征非常复杂，是典型的大应变大变形问题［2］，科研工作者不断地进行了研究，目前已经取得了很多有意义的成果。Rostami［2］采用全尺寸线性岩石切割机（LCM）实验对滚刀的破岩过程进行了研究，分析了盘形滚刀受力的规律。美国科罗拉多矿业学院（CSM）的Rostami等［3］基于实验提出了半理论的CSM预测模型。Bruland［4］基于工程数据建立的NTNU模型，能够对滚刀正压力和滚动力进行预测。Cho等［5］、程军等［6］采用有限元方法，对滚刀压痕试验与线性切槽试验进行仿真分析，并对TBM刀具破岩机理进行了研究，结合光滑粒子流体动力学（SPH）方法对TBM盘形滚刀在破岩接触区的受力特点进行了研究［7］。这些分析都是以正压力和滚动力为主，很少对侧向力进行研究。刘建琴等［8］应用非线性有限元分析软件ABAQUS，建立了单滚刀回转切削模型，得出回转切削时，安装半径较小的滚刀侧向力和滚动力相差不大甚至大于滚动力。夏毅敏等［9］在利用回转切削试验机（RCM）进行的实验中发现滚刀刀圈承受很大的侧向力。这些结果为进一步对滚刀侧向力研究建立了重要的理论与实验基础。

光滑粒子流体动力学是一种无网格数值方法，非常适合解决大变形、大应变、极大载荷情况时出现的网格扭曲和变形问题。在有限元网格划分时，通常采用删除单元的方式解决材料在滚刀作用下的脆性失效问题，但这样处理同时也会产生一定的误差［10］；而SPH方法会保留失效的粒子继续参与运算，可最大限度地减少这种误差。本文首先分析了盘形滚刀破岩过程的运动学规律，然后综合滚压破岩机理建立基于SPH的复合仿真模型，并利用实验数据进行验证，在此基础上对不同刀位安装半径的滚刀侧向受力进行分析，并进一步研究了刀间距、滚刀加载次序等因素对滚刀所受侧向力的影响问题。

1 盘形滚刀破岩点侧向运动分析

全断面岩石掘进机工作时，盘形滚刀与掌子面直接接触，在刀盘的驱动下既有公转运动也有自转运动。滚刀破岩点的运动轨迹为一条空间曲线。盘形滚刀旋转一周，破岩点参与破岩一次，破岩过程就是破岩刃上无数破岩点的破岩集合，因而破岩点的运动特点与滚刀受力密切相关。

根据滚刀空间运动规律，利用齐次矩阵（D-H矩阵）法对破岩点的运动规律进行分析，建立盘形滚刀破岩运动模型，如图1所示。为简化模型，选取了1/4的掌子面，其上是中心为O2的滚刀，滚刀半径为r，刀位安装半径为R，刀盘推进速度和距离分别为v和s，刀盘的转角和转速分别为q和w，滚刀自转角和转速分别为a和l。图中分别建立3个空间坐标系：通过刀盘中心轴线OZ轴的固定坐标系OXYZ，其中XOY平面为掘进机初始掘进面；与刀盘固连的动坐标系O1X1Y1Z1，原点O1在刀盘回转轴线上，并随着刀盘推进和旋转；与盘形滚刀固连的动坐标系O2X2Y2Z2，原点O2在滚刀中心处，绕Y2轴自转的同时绕刀盘中心轴线公转并随着刀盘整体推进。

图1 盘形滚刀滚压破岩运动示意图Fig.1 Motion diagram of rock breaking by disc cutter

在t时刻，a=λt，q=wt，由盘形滚刀作纯滚动得到rλ=Rw，全断面岩石掘进机掘进速度为v，且s=vt。可以得到盘形滚刀破岩刃上任意点K关于时间t的运动学方程为

式中：（xP，vP，zP）为k点的初始位置坐标，给定贯入度P，可得破岩过程中该破岩点沿刀盘径向的侧向位移ds为式中：t1为滚刀破岩点在开始破岩的时刻；t2为该点运动到最大侵深的时刻。

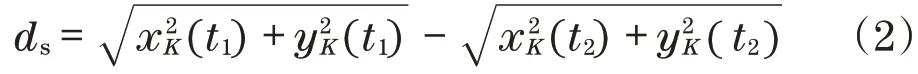
实际上，滚刀在掌子面上滚压运动会形成一个槽形压痕轨迹，槽形截面与滚刀截面形状有关，若刀圈截面为矩形，则槽形压痕的宽度w为

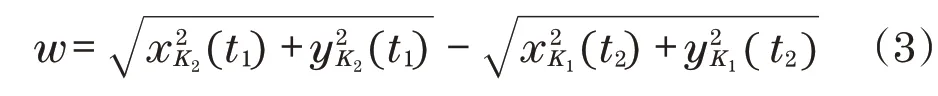
式中：K2为刀圈外侧破岩点；K1为相应刀圈内侧破岩点。

图2 为工程中常用的17”常截面（CCS）滚刀侧向位移随滚刀安装半径之间的关系曲线，滚刀直径432 mm，贯入度P=8 mm，刀尖宽度15 mm。由图可见，刀位安装半径较小时，刀尖侧向位移很大，然后随着刀位安装半径的增加迅速减小。由于滚刀的侧向位移，滚刀槽形压痕的槽宽均大于滚刀宽度，刀位安装半径越小，宽度越大，随刀位安装半径增加，逐渐趋向刀尖宽度。

同样当破岩点由最大侵深点返回到岩石表面的过程也会有侧向位移，而且与侵入过程的侧移方向相反，考虑到刀尖宽度因素，在破岩过程中，滚刀两侧都会由于侧向位移而受到复杂的侧向力作用。

2 数值仿真模型

盘形滚刀的破岩机理非常复杂，由于实验研究成本很高，而理论模型对复杂的工程环境适应性有限，近年来随着计算机技术的发展，数值仿真技术在盘形滚刀破岩机理研究领域应用越来越广泛。

2.1 数值模型建立

图2 不同刀位安装半径R的破岩点侧向位移和槽形压痕宽度的关系曲线（贯入度P=8 mm）Fig.2 Side displacement of the rock breaking point and the width of groove under different installation radius R（penetration is 8 mm）

根据盘形滚刀运动破岩规律，本文建立SPH粒子和有限元网格的复合仿真模型，如图3所示，模型包括滚刀（单刀或双刀）和岩石，滚刀包括刀圈和芯轴两部分。模型空间坐标系OXYZ位于刀盘旋转中心线和滚刀自转中心线的交汇处，R为刀位安装半径，D为刀间距。刀圈采用矩形截面模拟17常截面（CCS）的盘形滚刀，刀尖宽度15 mm。滚刀采用有限元网格划分，刀圈边缘两侧节点处各设置10个测量点，用于输出节点受力。滚刀刀圈材料具体参数如表1所示，芯轴设置为刚体，仿真过程中不考虑滚刀的磨损。对芯轴施加绕OZ轴的角速度ω，并带动刀圈公转，同时对刀圈施加绕芯轴转动的自转角速度为滚刀半径，模拟滚刀的滚动破岩运动。

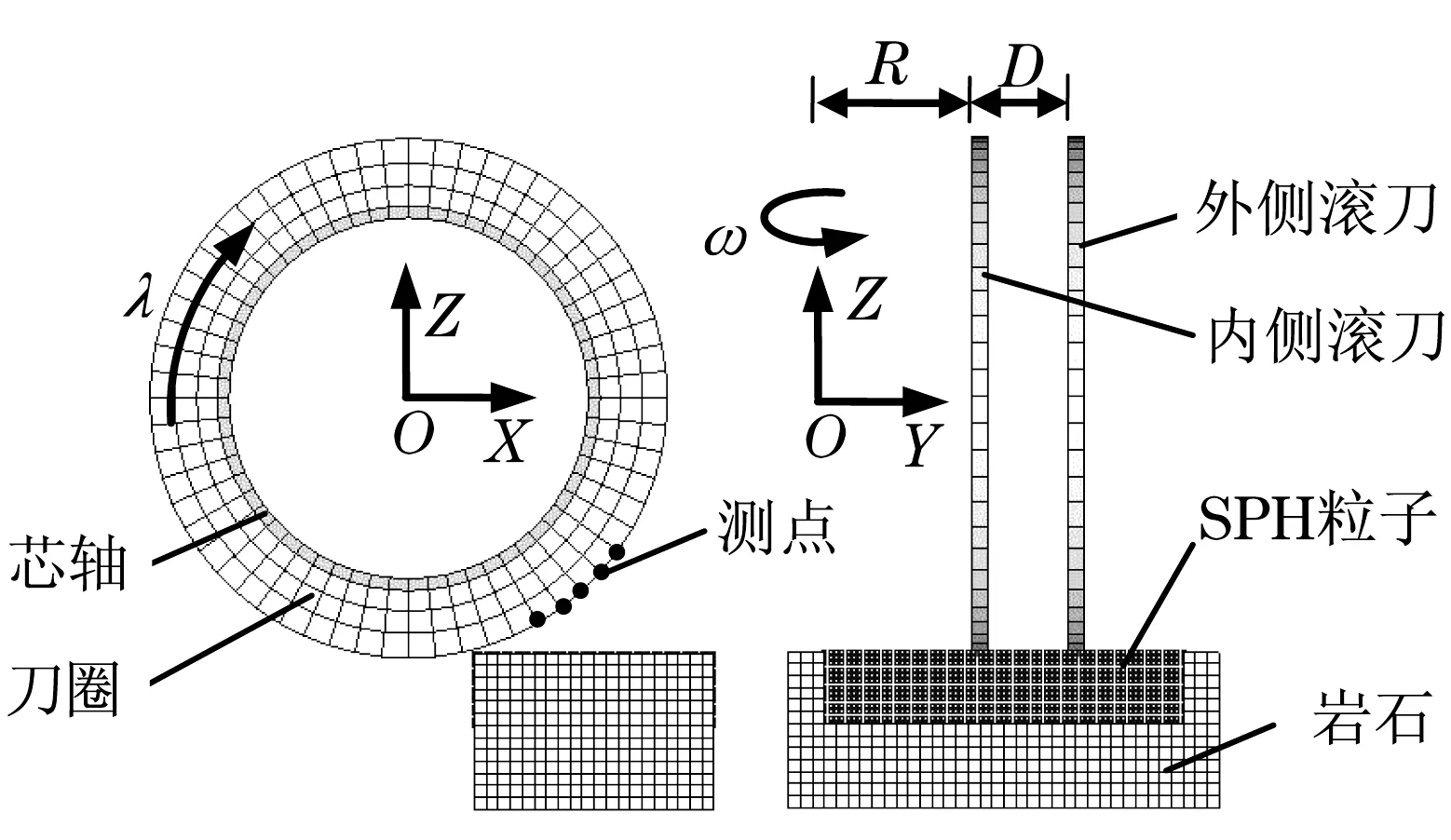
图3 盘形滚刀破岩过程的数值模型Fig.3 Numerical model for rock breaking by disc cutters

为节省计算时间，岩石采用复合网格划分，与滚刀接触的部分采用SPH粒子，其余部分划分为有限元网格，两者之间耦合连接。岩石底面施加固定约束边界条件，侧面约束垂直方向的运动。同时在这四周及底部施加透射边界条件，以防止反射回的应力波干扰，使岩石模型的尺度效应减小到最小。滚刀与岩石间接触设为拉格朗日/拉格朗日外部接触类型。

岩石采用本地花岗岩，假设为各项同性的均质材料，力学参数如表1所示。岩石的弹塑性本构行为用线性Drucker-Prager函数模拟，并结合Stassi硬化函数表达岩石的脆性行为。在盘形滚刀作用下，岩石的失效形式主要为拉伸断裂和剪切破坏为主，岩石材料的失效准则采用主应力/应变失效准则。考虑到岩石的动态破碎过程，选择失效准则中的裂纹软化选项。

表1 岩石和滚刀的力学参数［11］Tab.1 Mechanical parameters of rock and disc cutter［11］

2.2 模型验证

由于工程设计中还没有普遍接受的通用的侧向力预测模型，本文通过仿真模型中得到的正压力和滚动力数据，同线性切割试验（LCM）结果和CSM模型结果比较，以验证数值模型的正确性和可行性。

试验在北方重工盾构机国家重点实验室全断面岩石滚刀综合试验台上进行，如图4所示。该设备是在美国科罗拉多矿业大学线性切割机的基础之上重新优化设计的一台全尺寸线性切割机，能同时进行两把滚刀的滚压试验，可模拟刀盘在不同贯入度、刀间距下岩石切割过程。试验模拟盘形滚刀对岩石的顺次切削过程，即两把滚刀以一定的相位角顺次运动，当前刀产生的裂纹相对稳定后，再加载后刀。实验和仿真均采用相同方案，在滚刀贯入度P分别为3、5、8、10、12 mm，滚刀直线进给速度v=1 000 mm/s，刀间距s保持80 mm不变，进行系列试验和仿真。图5为试验过程高速照片。

图4 全断面岩石滚刀综合试验台Fig.4 Full size linear cutting comprehensive test machine

CSM模型美国科罗拉多矿业学院提出的盘形滚刀受力预测模型，包括正压力Fn和滚动力Fr，在国内外TBM设计中应用非常广泛，模型计算公式为

图5 试验过程照片Fig.5 Photos of the testing process

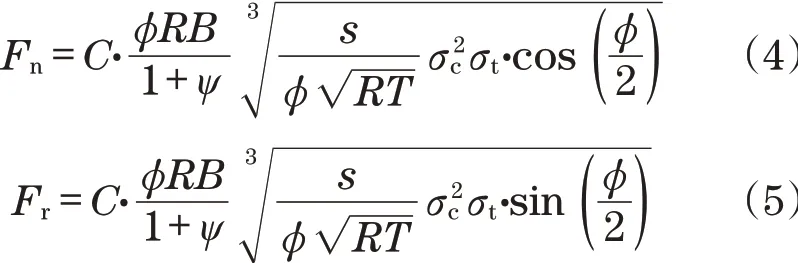
式中：φ为滚刀刀刃与岩石的接触角；R为盘形滚刀半径；B为滚刀刀刃宽度；ψ为滚刀刀尖压力分布系数，随着刃宽减小而增大，一般取-0.2～0.2；C为类似于φ角的无量纲系数，一般情况下C≈2.12；s为刀间距；σc为岩石单轴抗压强度；σt为岩石的抗拉强度。

为便于结果比较，均取滚刀受力稳定阶段的平均值，得到刀间距为80 mm情况下的平均正压力和平均滚动力，如图6所示。图中可见，曲线趋势基本一致，仿真得到的正压力和滚动力相对于CSM模型计算结果更接近于试验结果，因此，仿真模型能够反映滚刀破岩过程中受力规律，可以进一步对侧向力进行分析。

3 侧向力仿真及结果分析

3.1 刀位安装半径对滚刀侧向受力影响分析

为研究不同刀位安装半径盘形滚刀破岩过程中所受侧向力，模型采用单刀模式。滚刀公转角速度ω=3.4 rad/s，同时，根据不同刀位安装半径，对滚刀施加相应的自转角速度。利用刀尖两侧测点，测量破岩过程中各节点受力情况。图7为刀位安装半径为250 mm的仿真过程中岩石和滚刀的应力分布图。图中可知，有大量的粒子由于受滚刀的挤压从两侧大量飞出。

图6 仿真与试验和预测模型的比较结果Fig.6 Comparison results of simulation with test and CSM prediction model

图7 刀位安装半径为250 mm的应力分布图Fig.7 Stress of rock and cutter，which installation radius is 250 mm

仿真过程记录滚刀刀尖两侧测点的受力情况，图8为刀位安装半径为250 mm和1 000 mm时刀尖两侧测点侧向受力随时间变化的曲线，贯入度4 mm。实线表示刀尖内侧（刀盘回转中心方向）测点受力，虚线表示刀尖外侧测点受力。由图可见：内外受力差别很大，刀尖内侧受力大于刀尖外侧受力，而且方向相反。在时间上外侧稍微滞后于内侧，根据滚刀破岩点的运动规律，刀尖内侧一点在侵入破岩时，有一个向刀盘回转中心方向的侧向位移，因而引起侧向受力；而刀尖外侧点是在破岩点侵出过程中有一个向刀盘外侧方向的侧向位移而引起侧向受力，和内侧受力方向相反。

图9 为不同刀位安装半径刀尖一点所受最大侧向力的变化规律曲线，贯入度4 mm，刀盘转速为3.4 rad/s。实线为刀尖内侧测点，虚线为刀尖外侧测点。图中所见，刀位安装半径较小时刀尖内侧受力变化特别迅速，随着刀位安装半径增加，逐渐变小，而刀尖外侧一点受力则要相对平稳一些。滚刀破岩过程中所受侧向合力是破岩区所有接岩点受力的合力。图10为不同刀位安装半径的滚刀侧向力变化规律曲线，贯入度4 mm，刀盘转速为3.4 rad/s，蓝线为最大侧向力，红线为平均侧向力。由图可见，所有侧向受力均指向外侧，而且刀位安装半径小时侧向力较大，随刀位安装半径增加，逐渐变小。

图8 刀尖两侧测点侧向力受力随时间变化的曲线Fig.8 The curve of the lateral force of the measuring points on both sides of the disc cutter tip with time

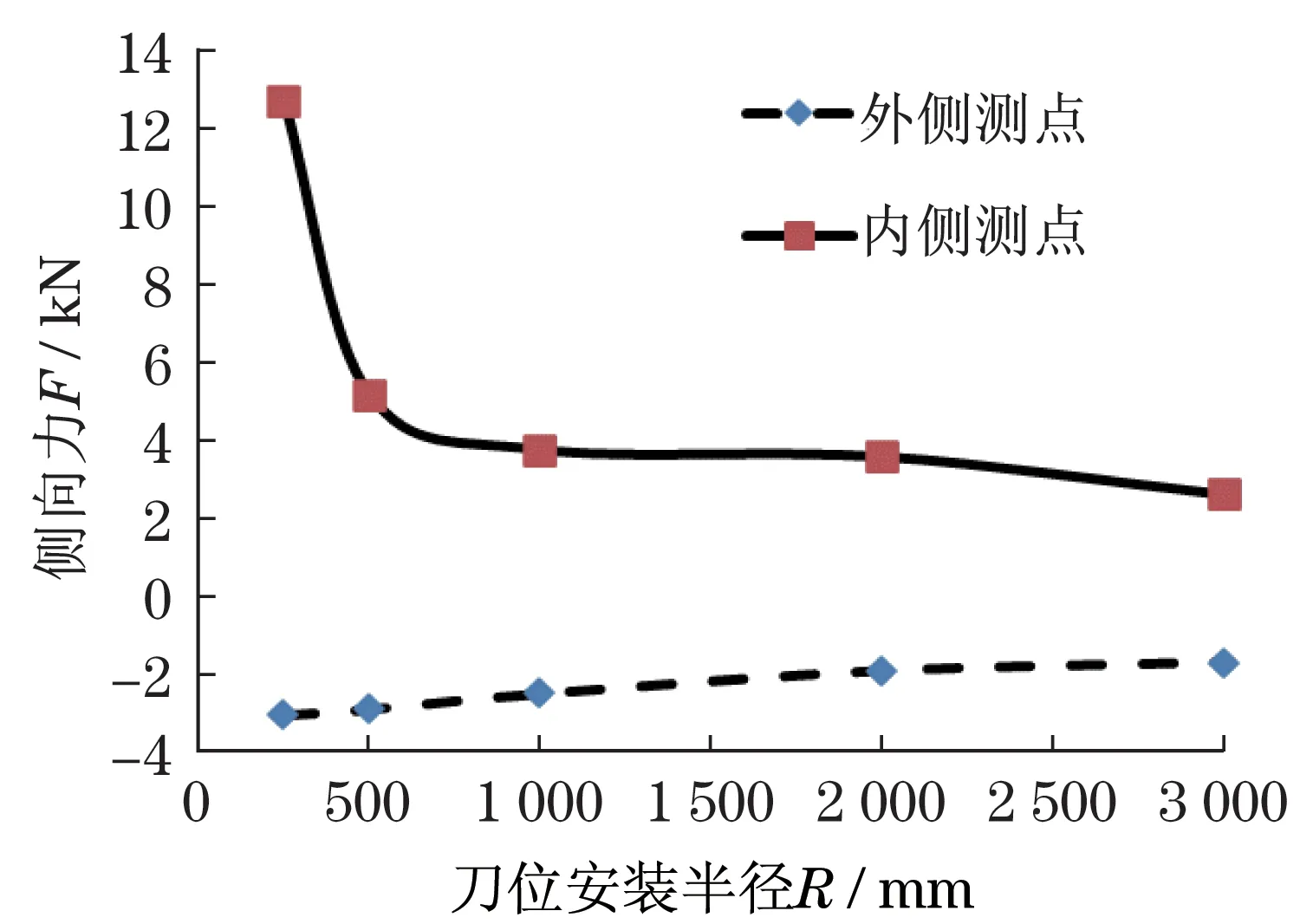
图9 不同刀位安装半径R刀尖测点所受最大侧向力Fig.9 The maximum side force on the measuring point of the cutter tip with different installation radius R

3.2 滚刀顺次切削时不同加载方式对侧向力的影响

图10 不同刀位安装半径R的滚刀侧向受力Fig.10 Side force on the disc cutter with different installation radius R

TBM工作过程中，刀盘上所有滚刀同时工作，正刀在刀盘的带动下顺次破岩，每一把滚刀都是在相邻滚刀破岩的基础上进行的，且滚刀一侧都会有一个临空面，影响破岩效果。考虑到滚刀回转破岩及相邻滚刀的内外加载顺序不同也对滚刀侧向受力产生影响，滚刀受力非常复杂。仿真采用不同刀间距的双滚刀模型，第1把滚刀刀位安装半径设为1 000 mm，先进行破岩；然后第2把滚刀进行破岩，研究第2把滚刀的破岩效果，模拟刀盘旋转过程中滚刀实际的破岩状态。仿真过程中贯入度保持4 mm。图11为滚刀顺次加载破岩仿真过程中的应力分布图，此时为内侧先行加载的状态。

图11 滚刀顺次加载破岩仿真过程中的应力图Fig.11 Stress diagram of sequential loading disc cutters during rock breaking simulation process

图12 分别为刀间距为40 mm时内侧先行和外侧先行破岩第2把滚刀侧向受力随时间变化关系的曲线。由图可见，由于加载顺序不同，对于40 mm刀间距，滚刀受力大小和方向不同，内侧先行时滚刀受侧向力指向刀盘中心，而外侧先行时滚刀受侧向力指向刀盘外侧。这是由于内侧滚刀先行加载后，对第2把滚刀的内侧受力有影响，使其减小，因而滚刀总侧向力减小，甚至改变方向；当外侧滚刀先行加载，正好相反，第2把滚刀外侧受力减小，导致总侧向力增加，因而内侧先行滚刀所受平均侧向力小于外侧先行情况。

图12 第2把滚刀破岩侧向力变化曲线，刀间距为40 mm Fig.12 The curve of force on the second cutter during rock breaking process，the cutter space is 40 mm

图13 为不同刀间距情况下滚刀侧向力的分布规律。实线为外侧滚刀先行加载，虚线为内侧滚刀先行加载。由图所见，当刀间距很小时，侧向力都很小，这是由于刀间距小，相应破岩量较小的缘故。随刀间距增加，两者都经过最大值后逐渐减小。当刀间距足够大时，由于相邻两刀互相影响变小，侧向力趋于相同。结果表明，滚刀旋转滚压破岩时，内侧先行加载时滚刀受侧向力较小，滚刀受力情况要好。

图13 不同刀间距的滚刀受侧向力Fig.13 Side force on the disc cutter under different space between two cutters

4 结论

（1）采用SPH方法对TBM盘形滚刀破岩过程进行三维数值仿真，可以得到盘形滚刀在不同工况下所受侧向力，在一定的情况下可以代替实验研究，节约研发成本。

（2）盘形滚刀破岩点在破岩过程中有侧向位移，内侧破岩点所受侧向力要大于外侧破岩点，而且方向相反。滚刀整体受力是所有破岩点受力合力的结果，刀位安装半径越小，侧向力越大，随着安装半径变大，侧向力迅速变小。

（3）滚刀回转破岩过程中，破岩临空面同加载顺序滚刀侧向力有很大影响，回转半径相同情况下内侧先行加载好于外侧先行加载，可以为刀盘布局设计提供参考。