高中数学解题教学的外显与内化——以几何题为例

刘锦发

（上杭县第一中学，福建 龙岩 364200）

数学解题教学是以数学问题为载体、学情为起点，通过深入分析问题的内在本质，总结解决的一般方法，让学生理解数学、学会“数学的思维”的教学活动.它关注的不单是解题的“结果”，更在乎解题的“过程”，引领学生体验“探路”的经历是解题教学的关键.没有人怀疑过解题教学对数学学习的重要作用，但不同的人对解题教学的理解和操作却有很大差别.不少教师有重一招一式的归类，轻思想方法的提炼；多讲“怎样解”、少问“为什么这样解”等教学弊端，当引以为戒.

一、教学理念应从“教解法”转向“教想法”

学生解题受阻多数源于所学知识与需要解决的问题无法链接，思考过程中出现知识断层，或者所用知识与解题缺乏一定的逻辑关系.因此，解题教学要善于帮助学生消除思维定式的负迁移，在问题的疑难处设置问题串，诱导学生深入分析，让其知道解法的由来，尽量避免直接抛出解法的做法.

（1）将C 和L 化为直角坐标方程；（2）求C 上的点到L 距离的最小值.

本题条件中所给的椭圆参数方程和课本所学的离心角为变量的形式有明显不同，这是学生解题障碍之处.教学中，教师可通过问题的分解来引导学生“探路”：

二、课堂立意应从“解题技能”转向“思想方法”

数学是思维的体操.解题教学不只是教学生会解这一个题目，不可只强调解题的技能技巧，而应全方位、多角度地引导学生深入挖掘其蕴含的思想和方法，要通过问题的解决把知识与知识之间的关系紧密联系起来，并在此过程中获得数学活动的基本经验.只有让学生充分感悟其中的数学思想，才能使学生获得更多的积累和提升.

例2：直线L过点P(-4,0)，与圆C:(x-1)2+y2=5交于A、B两点，A是线段PB的中点，求直线L方程.

这是某老师在一次解题教学公开课的案例，大致过程如下：

上述教学过程更多的是教师展示解题技能，学生除了“赞叹”之外可能就是“茫然”，是一题多解教学的常见误区（如法4 圆幂定理几乎没有学生知道，法5 也很少学生可以想到）.解题教学要帮助学生理清各种解法的思考视角，还要对不同方法进行比对，使之产生顿悟（本题中的顿悟就是“方程思想”），从而让学生明白：“方程思想”是解决解析几何题的基本思想方法.如法3 就是“方程思想”下的简解，不会给学生留下“总是用韦达定理”的错觉.而“方程思想”恰恰是本题教学需要达到的高度，而该教师缺乏这样的意识，没有把教学中核心和本质的东西点出来，是明显的教学不足.

三、问题解决应从“教师展示”转向“学生探究”

教学是教师与学生之间的双向活动，在教师主导的前提下，更需要增强学生的主体地位，让学生深度学习才能有效提升思考能力.解题教学不是让教师展示解题结果，而要引导学生积极参与解题全过程，经历如何决定解题的方向、如何选择解题的方法、如何完成解题的方案等过程，诱导学生主动深入地学习.将知识的传递过程转变为引领学生共同探究的过程，让教师思维“可视化”，从中学会“找路”的方法.

例3：平面单位向量a、b满足a⊥b，且(a-c)·(b-c)=0，求向量c的模的取值范围.

此题很多学生觉得无从下手，教师在教学时，可先引导学生思考：

（1）题目知道的条件有哪些？

（2）需要探求的问题是什么？

（3）题目与什么数学概念相关？

（4）此题转化的关键是什么？

（5）方程(a-c)·（b-c)=0 有哪些处理策略？

经过一番探究之后，再让有思路的同学说“思维过程”：

施教之功，贵在引路，妙在开窍.该教师的教学没有自己抛出题目答案，而是通过剖析题目要素，促进学生探寻各信息间的连接点，在学生说“思维过程”的基础上，逐步深入对问题本质的认识，慢慢形成解题方案.在互动的过程中，让不同学生之间的思维不断碰撞，并从中发现“数化”和“形化”是平面向量问题的常用处理策略.

四、能力发展应从“解决问题”转向“审题和反思”

解题教学的关键不是“解题”，而是“教学”.教师要善于让学生知晓：条件怎样发散？结论怎样集中？怎样从条件中获取怎样解这道题的逻辑起点、推理目标及沟通起点与目标之间联系的更多信息；并在解后能将自己的解题活动作为思考的对象.在总结提升中实现从“一题”到“一类”的转变，才能真正学会分析问题和解决问题的方法，学会审题和解后反思是学生能力发展的关键.

反思3：思维障碍是什么?解决途径有哪些？用到了哪些方法？这些方法是如何想到的?它们体现了什么数学思想？

经历上述反思过程，能帮助学生理顺解题的逻辑关系，形成规范化思考问题的品质；领会运算对象的多样性和数学运算应用的广泛性，从中提炼对以后的解题有指导意义的信息，涵育数学建模素养.

五、解后反思应从“流于形式”转向“真正落实”

解题教学是一个递进的过程，没有让学生经历“感”“悟”，教师讲得再透彻，学生在作业或考试中未必能快速正确解题.有些教师浅尝辄止，讲完一题马上就讲下一题.其实，只有真正落实解后反思，通过问题将学生引向反思解题过程的思维偏差处、易混易错点、关键点是如何突破的，方法可否进行完善和优化，题目的背景是什么，能否进行变式、推广和延伸等，特别要重视对问题本身和学生解题过程的剖析，才能提高辨别能力和解题应对能力，将学生的思维引向更深处.

例5：点P(1,2)在抛物线C：y2=2px上，直线l经过点Q(0,1)，且与抛物线交于A,B两点，直线PA、PB 分别交y 轴于点M,N.

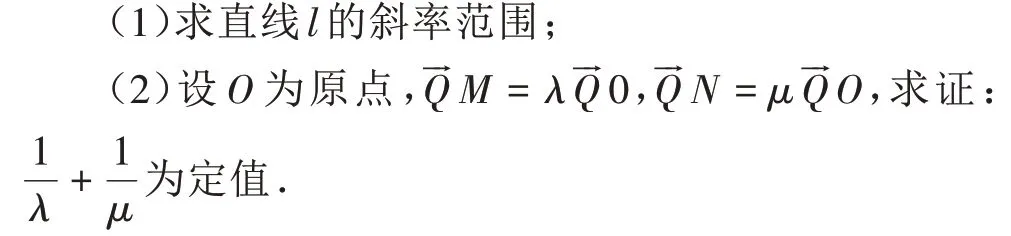
本题是解析几何中经典的定值问题，教师可从以下途径引导学生解后反思：

反思1：直线PQ与抛物线的位置关系是什么？（容易验证直线PQ是抛物线的切线，同时y轴也是该抛物线的切线）.

反思2：处理定点、定值问题的通性通法是什么？（通过设参数或取特殊值来确定，或将问题涉及的几何式转化为代数式、三角问题，再证明该式是恒定的）.

反思3：若将抛物线改为椭圆、双曲线，结论是否成立？（结论仍然成立：设Q点是圆锥曲线K“外部”任意一点，过点Q分别引圆锥曲线K的两条切线QP,QR，切点分别为P,R，过点Q 分别引圆锥曲线K的“割线”，与其交于A,B两点，直线PA、PB与另一条切线QR交于M,N，若

反思4：如果圆锥曲线的两条切线改为两条割线，结论是否成立？（结论仍然成立：设ANCD是圆锥曲线K的内接四边形，直线AB,CD相交于点O，过O任作一直线l与K交于R,S两点，且与直线AC,BD分别相交于P,Q，则

设计这样的问题让学生去反思，能有效调动学生主动深入思考，驱动学生寻找试题在高等数学中仿射几何的背景，在问题的拓展与变式过程中探究不变的本质，在不变的本质中寻找变的规律性，才能有效防止学生套题型、机械模仿现象的发生，也才能促进学生“四基”的形成和“四能”的提升.

数学解题教学策略多种多样，但必须得法！除了上述策略之外，还必须基于学情，要理解学生，要有站在学生的立场和循序渐进的恒心，让学生有“说”的机会、“思”的途径、“问”的时间、“悟”的时间，才能将外显的解题教学活动内化为学生的思维活动.