多重Ⅰ型混合截尾样本的Weibull分布参数估计*
秦 睿
(广西师范大学数学与统计学院,广西桂林541004)
0 引言
在产品的可靠性试验,生物医学实验的寿命评估,工程学的疲劳可靠性分析等领域中,受到试验时间和成本等因素的影响,大量试验产生了不完整数据,实际生活如在临床医学研究中,由于研究成本、研究对象失访或中途退出研究、研究对象因其他情况死亡等因素,造成研究人员无法观察所有研究对象完整的试验过程,出现收集到不完整数据的情形。例如,定时截尾、定数截尾、混合截尾等都是不完整数据情形,其中多重Ⅰ型混合截尾情形在实际生活中广泛存在。
为了解产品的可靠程度,工程学的材料耐疲劳程度等各项指标,研究人员需要从上述不完整数据情形中统计分析相应的结果。不同于完整数据样本的统计分析,截尾样本需要提前对样本数据进行处理后,选择适当的统计方法才能得到比较可靠的结果,为研究人员的决策提供依据。
现已有大批专家学者对Ⅰ型混合截尾样本进行了大量的研究。在Ⅰ型混合截尾方案测试中有n个寿命是独立同分布的随机变量x,当测试中有m(m≤n)个单元失效或者测试时间达到预先设定的测试停止时间T,则整个测试停止,此时分别有如下两种数据情况,第一种当测试中有m(m≤n)个单元失效,则能够观察到m个完整的寿命数据为x1,n≤x2,n≤…≤xm,n,测试停止时间为xm,n;第二种当测试时间达到预先设定时间T,则能够观察到d个完整的寿命数据为x1,n≤x2,n≤…≤xd,n,其中d<m,xd,n≤T<xd+1,n,测试停止时间为T。整个测试系统的停止时间定义为min{xm,n,T}。Epstein(1954)在文献[1]中提出Ⅰ型混合截尾方案次序统计量的应用。在分布已知的情况下,陈家鼎(1989)在文献[2]证明了基于随机截尾数据的威布尔分布参数最大似然估计具有强相合性;刘焕彬(1994)在文献[3]中证明了在Ⅰ型混合截尾情况下最大似然估计的强相合性。Bedbur(2019)等在文献[4]中研究了多重序贯次序样本下威布尔分布参数的统计推断,证明了最大似然估计的一致性和渐近有效性。Górny(2020)等在文献[5]中讨论了在多重Ⅰ型混合删失序贯样本情况下指数分布的最大似然估计,并用实际样本数据证明了估计的有效性。目前针对多重Ⅰ型混合截尾样本情形的参数估计鲜有人研究。因此,本文利用最大似然估计方法对多重Ⅰ型混合截尾样本情形下的两参数威布尔(Weibull)分布参数进行估计。
1 参数估计
假设寿命随机变量X服从一个比例参数和形状参数分别为λ和c的两参数威布尔分布,其关于随机变量X的概率密度函数(PDF)和累积分布函数(CDF)分别为

其中,比例参数(scale parameter)λ≥0 和形状参数(shape parameter)c≥0。
多重Ⅰ型混合截尾方案是指,假设测试人员能够观察到试验样本的寿命为Xij,1≤i≤k,1≤j≤mi,其中设测试系统有k个测试组,第i个测试组有ni个试验样本,设定第i个测试组的固定失效数为mi(mi≤ni)和测试停止时间为Ti>0,1≤i≤k。则多重Ⅰ型混合截尾的第i组第j个次序统计量为

第i组测试停止时间为
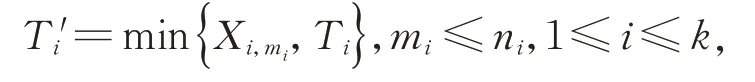
第i组测试观察到失效个数为

其中I(-∞,Ti](x)表示x的示性函数,即x∈(-∞,Ti]示性函数为1,否则为0。整个测试观察到失效的总个数为

参考Kamps U(1995)在文献[6]中提出的次序统计的联合密度函数,则关于多重Ⅰ型混合截尾样本下威布尔分布的参数λ和c的似然函数定义为

将两参数威布尔分布的PDF(1)式和CDF(2)式带入(3)式得到似然函数

为求解当(4)式达到最大时的参数λ和c的估计值̂和̂,需要先对(4)式取对数得

其中ai是独立于参数λ和c的常数。
把对数似然函数(5)式分别关于参数λ和c求偏导并令为0 得下式

因此,最大似然估计̂和̂只需满足下式即可

通过(6)式可以看出,最大似然估计̂和̂没有具体的显示表达式,因此在计算估计值上采用简单有效的牛顿-拉弗森方法(Newton-Raphson method)迭代求解(6)式方程组。
设

则牛顿-拉弗森方法迭代方程为

其中

具体参数λ和c的牛顿-拉弗森方法迭代算法描述如下,假设预先给定一个非常小的常数γ,本文给定γ=10-8,
(1)给定迭代次数l=0, 初始值λ0和c0;
(2)根据(7)式计算并更新cl+1;
(3)根据(7)式计算并更新λl+1;
(4)如果|cl+1-cl| <γ成立,则停止迭代,输出参数最大似然估计值
(5)否则重复步骤(2), (3), (4), (5)。
最大似然估计的精度可以用偏差和均方误差来表示,也能展现出估计值的稳定性,但不够直观。置信区间能简单和直观地给出参数估计值的精度和可靠程度。本文基于Thoman D R(1969)等文献[7]中的定理A 和定理B 构造参数的精确置信区间。
在参数λ=1 和c=1 的威布尔分布情形下,设参数λ和c的最大似然估计分别为和。根据文献[7]定理Ac独立于参数λ和c的分布,且与具有相同的分布。其中̂为多重Ⅰ型混合截尾样本下威布尔分布参数c的最大似然估计。因此,可用的分布来构造未知参数c的置信区间。
设l1,l2为任意两个常数,使得下式在置信水平为1-α的条件下成立

由于与同分布,将=代入(8)式可 得,

最终可得,置信水平为1-α的威布尔分布参数c的置信区间为

设t1,t2为任意两个常数,使得下式在置信水平为1-α的条件下成立


最终可得,置信水平为1-α的威布尔分布参数λ的置信区间为

2 模拟研究与实例分析
假设两参数威布尔分布参数真值分别为λ=2 和c=2,那么对应参数估计的偏差(BIAS)和均方误差(MSE)见表1。
表1 展示的是样本总量分别为50, 100, 200, 500 的比例参数λ和形状参数c都为2 时的两参数威布尔分布,在b= 3 5 的多重Ⅰ型混合截尾方案下参数最大似然估计的偏差(BIAS)和均方误差(MSE)。根据表1 可以看出,最大似然估计的偏差和均方误差都随样本总量的增大而减小,说明参数的最大似然估计表现出良好的稳定性和有效性。

表1 最大似然估计的偏差(BIAS)和均方误差(MSE)
表2 展示的是分组比例分别取1/2, 3/5, 4/5 中不同值时,比例参数λ和形状参数c都为2 时的双参数威布尔分布,在样本总量为100 的多重Ⅰ型混合截尾方案下参数最大似然估计的偏差(BIAS)和均方误差(MSE)。根据表2 可以看出,最大似然估计的偏差和均方误差均随分组比例的增大而减小,说明最大似然估计是符合实际情形和逻辑,可应用性较好。

表2 b 取不同值时参数估计的偏差(BIAS)和均方误差(MSE)
实际案例分析数据来源于Proschan(1963)在文献[8]给出并讨论的13 架波音飞机空调系统的故障时间间隔(小时)数据,规定飞机完整运行2000 小时后,必须对飞机进行保养维护工作。Proschan(1963)对数据进行分析发现每架飞机空调系统的故障时间间隔分布呈形状参数c为1 的威布尔分布。
我们考虑使用飞机编号为7808 至7814 的7 架飞机空调系统故障时间间隔观察值数据,对数据进行处理后应用多重Ⅰ型混合截尾方案,即在整个过程中,共有k=7 组数据,设定每组观察都观察25 次,即ni=25,1≤i≤k,规定飞机在保养维护周期内出现14 次及以上空调故障,就必须进行保养维护工作,即固定观察失效数量mi=14,1≤i≤k,固定停止时间为Ti=2000,1≤i≤k。则通过实际观察值可以得到如下变量的数值,每架飞机保养维护周期的运行时间(停止时间)为

每架飞机保养维护周期内空调故障次数(失效个数)为
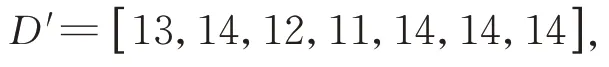
利用最大似然估计方法对多重Ⅰ型混合截尾样本情形下的两参数威布尔分布参数进行估计,得到比例参数的最大似然估计̂=1952.12 和形状参数的最大似然估计̂=1.05,其分布的总体均值为1999.07。
从得到的结果可以看出,将本文的估计方法运用到实际案例中,得到的结果是良好,可接受。前人学者已证明了上述数据服从形状参数c为1 的威布尔分布,此处的形状参数估计值为̂=1.05,两者相差很小,也符合数值模拟研究给出的结果。此外,通过比例参数和形状参数的最大似然估计计算出的总体均值为1999.07,表示在保养维护周期内飞机运行时间为1999.07 小时,即飞机空调故障时间满足飞机运行2000 小时强制保养维护规定,保证了飞机运行时的安全性和可控性,说明方法是可应用性良好,符合实际情况。
3 结论
本文探究了在多重Ⅰ型混合截尾样本情形下,两参数威布尔分布的参数估计问题。将多重Ⅰ型混合截尾样本进行次序统计量处理后,得到次序统计量的联合密度函数,进而使用最大似然估计方法计算得到参数估计,利用牛顿-拉弗森迭代法求解出参数估计值,并给出参数的精确置信区间。数值模拟研究与实例分析结果表明,基于最大似然估计方法能快速得出参数的估计和精确置信区间,同时参数估计值表现出良好的稳定性和可应用性。此外,在求解参数估计值时,使用了牛顿-拉弗森迭代法,可能会使参数估计值陷入局部最优解中,不能得到更加准确的参数估计值,后期需要在参数估计值求解的方法上进一步加强。另外,后续可以考虑使用贝叶斯估计等其他方法估计参数。

