基于贪婪元胞遗传算法的工序排序优化问题*
邓燕兰,熊菊霞,郑宏宇,姚光磊
(广西民族大学数学与物理学院,广西南宁530006)
0 引言
计算机辅助工艺设计(Computer Aided Process Planning, CAPP)在计算机工艺规划等方面有重要的应用。[1]CAPP 主要分为三步:第一,特征识别,即对零件的特征进行分类和识别;[2]第二,确定提取出来的特征的加工操作和加工资源;[3]第三,在设计和制造实践的条件约束下,确定加工成本最低的操作顺序及其对应的加工资源。[4]工序排序优化问题属于第三步,在已知加工特征,及其每个特征的加工操作和候选加工资源的基础上,通过规划得到最优加工方案。它以最小化总成本为目标;以确定满足优先关系约束的加工工序的顺序,以及每个加工工序使用的加工资源为主要任务。
工序排序优化问题的可行方案包括可行工序序列(Feasible Operation Sequence, FOS),及FOS 中每个工序对应使用的机床资源、刀具资源和进刀方向(Tool Approach Direction, TAD)。工序的排序,候选加工资源的选择是相互联系、相互制约的,因此工序排序优化问题已被证明是一类具有NP-hard 性质的组合优化问题。[5]它的求解方法主要分为两类:一类是精确方法,主要包括分枝定界法[6]和线性规划法[7];另一类是近似方法。近几年来随着智能优化算法的发展,很多专家和学者都开始利用智能优化算法求解组合优化问题。[8]针对工序排序的优先级限制,Li等人[9]提出了求解工序排序优化问题的混合遗传算法和模拟退火算法,使用优先约束调整算法对交叉和变异后生成的不可行解进行修复。Huang 等人[10]将图论与矩阵理论相结合,提出了一种混合图遗传算法,采用启发式算法将变异算子生成的不可行方案调整到可行域。Yun 等人[11]提出了基于拓扑排序(TS)的遗传算法,利用优先关系的有向无环图生成FOS,有效处理了初始种群加工工序的优先关系约束问题。Su 等人[4]提出了求解工序排序优化问题的改进遗传算法(ESGA),设计了使交叉后染色体仍然满足优先关系约束的交叉算子,在迭代过程中保持了加工方案的可行性。窦建平等人[12]提出基于可行工序序列的遗传算法(FOSOGA),设计了保持加工方案可行性的交叉算子和变异算子。除此之外,也有很多其他的算法应用在工序排序优化问题的求解中,比如Guo等人[13]提出了求解工序排序优化问题的粒子群算法(PSO),Hu 等人[14]提出了求解工序排序优化问题的蚁群算法(ACO)等。
元胞遗传算法(CGA)是将遗传算法(GA)和元胞自动机相结合而形成的一种新的算法,利用元胞自动机的邻域结构实现遗传算法的选择操作,使其更符合现实世界的生物进化特点,通过重复的局部相互作用,实现全局计算。[15]CGA 算法在组合优化问题中具有广泛的应用,例如:旅行商问题[16]、无线电能传输网路径寻优问题[17]、柔性车间调度问题[18]等。但是,目前CGA 算法在工序排序优化问题上的应用还很少。本文在CGA 算法的基础上引入拓扑排序算法(TS)、贪婪算法和精英个体保留策略,提出一种求解工序排序优化问题的贪婪元胞遗传算法(GCGA),从而有效地解决工序排序优化问题。
GCGA 算法与现有求解工序排序优化问题的遗传算法相比,其新颖之处主要在于:将CGA 算法应用于工序排序优化问题的求解,通过元胞自动机的邻域结构避免陷入局部最优;引入贪婪算法生成初始种群的加工资源,降低初始种群中染色体的总成本;分别在交叉和变异后设置精英个体保留策略,避免劣解进入种群。
1 工序排序优化问题
1.1 问题描述
工序排序优化问题涉及加工工序排序、机床选择、刀具选择和TAD 选择四个方面。加工工序排序受到优先关系的约束,其约束可以用有向无环图来描述,一般称此有向无环图为工序优先图,如图1 为案例ANC-101 的工序优先图。[4]由于有向图在运算时不方便使用,所以本文使用优先矩阵来表示工序的优先关系。

图1 ANC-101 的工序优先图
机床、刀具和TAD 的选择受到实际制造生产的约束,只能从候选资源中进行选择。选择不同的加工资源会产生不同的加工成本,具体的加工成本分为五部分:机床成本、刀具成本、机床变换成本、装夹变换成本和刀具变换成本。产生上述变换成本的情况由表1~3 所示。

表1 机床变换条件

表2 装夹变换条件

表3 刀具变换条件
由表1~3 可以看出,在连续两次加工中使用不同的机床,将会产生机床变换成本;在连续两次加工中使用不同的机床或者不同的TAD,将会产生装夹变换成本;在连续两次加工中使用不同的机床或者不同的刀具,将会产生刀具变换成本。因此,最小化总成本意味着最优加工工序序列的机床、刀具和TAD 的变换次数较少。[19]
1.2 数学模型
工序排序优化问题的加工成本包括:机床成本、刀具成本、机床变换成本、装夹变换成本和刀具变换成本。为计算成本引入表4 的符号定义,具体的计算公式如下。

表4 符号定义
总的机床成本,即所有加工工序所使用的机床成本之和,记为:TMC。工序数量为:N。

总的刀具成本,即所有加工工序所使用的刀具成本之和,记为:TTC。

总的机床变换成本记为:TMCC,机床变换次数记为:NMC。
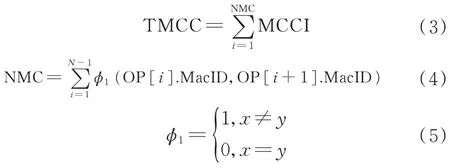
总的装夹变换成本记为:TSCC,装夹变换次数记为:NSC。


总的刀具变换成本记为:TTCC,刀具变换次数记为:NTC。
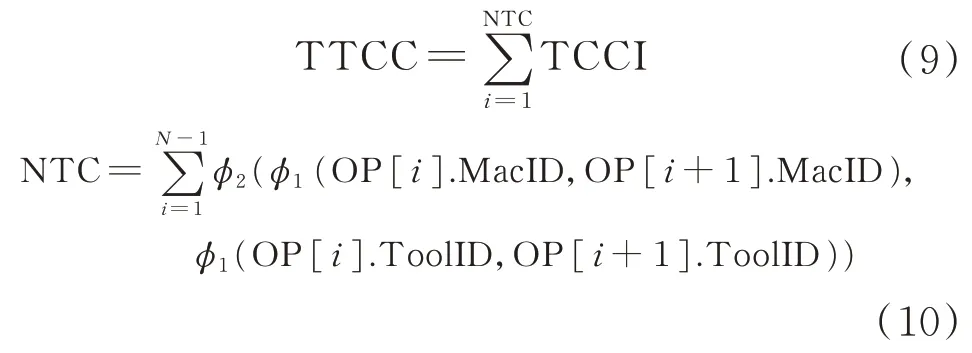
总成本记为:TC,成本的权重分别为:w1,w2,w3,w4,w5。

2 贪婪元胞遗传算法(GCGA)
贪婪元胞遗传算法(GCGA)在元胞遗传算法的基础上,针对工序排序优化问题的特点,使用拓扑排序算法(TS)生成初始种群的可行工序序列(FOS),引入贪婪算法生成初始FOS 的加工资源,并且使用结合精英个体保留策略的交叉算子和变异算子来保持解的可行性和避免劣解进入解空间。
2.1 种群初始化
工序排序优化问题的可行方案包括FOS 及其对应的加工资源,加工工序使用整数编码方式进行编码,加工资源使用对应编号表示,表5 给出了案例ANC-101 的一个最优方案。初始种群的产生可分为两个方面:FOS 的生成和加工资源的生成。

表5 ANC-101 最优解
2.1.1 FOS 的生成
为了方便计算机计算,本文使用优先矩阵表示加工工序的优先关系。优先矩阵由0 和1 组成,若第i行第j列的值为1,则代表工序i需要在工序j之后执行,否则工序i和工序j无优先关系。因此,整行全部为0 的工序表示此工序不需要在其他工序之后操作,可以选择此工序作为第一个操作工序。当执行完第一个操作工序之后,原来需要在此工序之后执行的操作就不再受此工序的约束,即可以将此列的所有非零值更改为0。使用优先矩阵进行工序排序的过程与TS 使用有向图生成FOS 的过程是类似的。
FOS 的生成步骤如下:
1)通过加工工序的优先关系得到优先矩阵。
2)随机选出一个整行全部为0 的工序i(与之前选择过的工序不重复)作为当前操作的工序。
3)用0 替换第i列的所有值为1 的位置。
4)重复2)和3),直到确定所有工序的次序。
下面展示了含有5 个加工工序的可行工序序列的生成示例。
1)生成优先矩阵,如图2(a)所示,此时矩阵第1、2行的值全为0,可随机选择工序1 和工序2。
2)若选择工序1,则将矩阵第1 列的值全更改为0,得到的优先矩阵如图2(b)所示。此时矩阵第1、2 和3 行的值全为0,除去已选择的工序1,可随机选择工序2 和工序3。
3)若选择工序3,则将矩阵第3 列的值全更改为0,得到的优先矩阵如图2(c)所示。此时矩阵第1、2 和3 行的值全为0,除去已选择的工序1 和工序3,只有唯一选择工序2。
4)选择工序2,并将矩阵第2 列的值全更改为0,得到的优先矩阵如图2(d)所示。此时矩阵第1、2、3 和4 行的值全为0,除去已选择的工序1、2 和3,只有唯一选择工序4。

图2 可行工序序列生成示例的优先矩阵
5)选择工序4,此时只剩唯一选择工序5,故直接选择工序5,完成工序排序操作,最后得到的工序为1-3-2-4-5。
2.1.2 加工资源的生成
加工工序的加工资源分为3 个部分:机床、刀具和TAD,每一个工序都有其候选的加工资源,从中选择不同的加工资源会产生不同的成本。若是从候选资源中随机选择加工资源,则得到的总成本会具有较大的随机性,导致优化性能的降低。为此,本文将贪婪算法应用于初始FOS 的加工资源的生成,降低初始解的总成本。使用贪婪算法生成FOS 的机床资源的具体步骤如下:
1)选择第一个操作工序的候选机床中成本最低的机床作为此工序使用的机床。
2)从第二个操作工序开始执行以下步骤:
a)选择当前操作工序的候选机床中成本最低的机床Mac1。
b)选择上一个操作工序使用的机床Mac2。
c)如果Mac2并不是当前操作工序的候选机床,或者和Mac1相同,则令当前操作工序使用的机床为Mac1。否则执行下一步。
d)计算使用Mac1产生的成本C1和使用Mac2产生的成本C2。

e)如果C1<C2,则令当前操作工序使用的机床为Mac1,否则为Mac2。
使用贪婪算法生成FOS 的刀具资源和TAD 的步骤与上述使用贪婪算法生成FOS 的机床资源的步骤是类似的。若是刀具的选择,则成本的计算公式更改为刀具成本、机床变换成本和刀具变换成本之和;若是TAD 的选择,则由于TAD 本身不产生成本,因此无需计算成本,直接使用上一次操作工序的TAD,或者在候选资源中随机选择。
2.2 交叉和变异
交叉算子和变异算子是遗传算法的精髓,是影响算法优化性能的重要因素。[20]由于工序排序优化问题的加工方案分为FOS 和FOS 的加工资源两部分,所以需要分别对FOS 和FOS 的加工资源进行交叉和变异。本文设计了结合文献[4]提出的交叉算子、文献[12]提出的变异算子和精英个体保留策略的交叉算子和变异算子,在对FOS 执行交叉和变异时能够保持FOS 的可行性,并且使用精英个体保留策略决定保留的染色体,符合优胜劣汰的自然法则。
2.2.1 交叉
针对工序排序优化问题,本文先是在保持加工工序的加工资源不变的情况下对加工序列进行双点交叉,交叉后比较母体和子代染色体的总成本,保留总成本较少的染色体。其次,在保持FOS 不变的情况下,分别使母体FOS 的每个加工工序的加工资源以0.5 的概率变为另一个母体的对应工序的加工资源,得到新的子代染色体再和母体进行比较,同样保留总成本较少的染色体。
针对母体P1和P2的FOS 的交叉步骤如下:
1)随机生成两个切点k1和k2,同时令Q1=P1,Q2=P2。
2)选择Q1中位于k1和k2两切点之间工序Q1(k1:k2),在P2中找到工序Q1(k1:k2)。
3)以P2中工序Q1(k1:k2)的先后顺序重排Q1(k1:k2),但不改变工序的加工资源,即可得到P1的子代Q1。
4)使用Q2和P1分别替代Q1和P2执行第2 步和第3 步,得到P2的子代Q2。
5)分 别 计 算P1、P2、Q1和Q2的 总 成 本S1、S2、T1和T2。
6)如果S1>T1或S2>T2,则 令P1=Q1或P2=Q2,否则不保留Q1或Q2。
FOS 进行交叉操作之后得到的子代染色体的加工工序仍然满足工序优先关系的约束条件,保证了解空间的可行性。此外,针对FOS 的交叉操作不改变加工工序的加工资源,所以子代染色体的机床成本和刀具成本是不变的。但是,加工工序顺序的改变可能会使机床变换成本、装夹变换成本和刀具变换成本发生改变。所以,为了避免劣解进入解空间,FOS进行交叉操作后再进行精英个体保留策略是非常有必要的。同时,加工资源的选择也是影响总成本的重要因素,FOS 进行交叉后需要再对加工工序的加工资源进行交叉。针对母体P1和P2的FOS 的加工资源的交叉步骤如下:
1)令Q3=P1,Q4=P2,从母体P1的第一操作工序开始执行第二步。
2)生成 随 机 数r,若r>0.5,则选择P2对应工序的加工资源作为Q3的加工资源。
3)对所有的加工工序执行完第2 步后,即可得到P1的 子代Q3。
4)令Q4和P1分别替代Q3和P2执 行第2 步,得到P2的 子代Q4。
5)分 别 计 算P1、P2、Q3和Q4的 总 成 本S1、S2、T3和T4。
6)如果S1>T3或S2>T4,则 令P1=Q3或P2=Q4,否则不保留Q3或Q4。
2.2.2 变异
为了保持FOS 的可行性,使用结合TS 的双点变异。同时,在对FOS 进行变异操作之后进行与交叉操作类似的精英个体保留策略。针对FOS 加工工序的加工资源的变异操作,以0.5 概率将原加工资源替换为随机选择的候选资源中的加工资源。对母体P的变异操作的具体步骤如下:
1)随机生成两个切点k1和k2,同时令Q=P。
2)选择Q中位于k1和k2两切点之间工序Q(k1:k2),生成工序Q(k1:k2)的优先矩阵。
3)按照2.1.1 中生成FOS 的步骤生成工序Q(k1:k2)的新次序并取代旧次序,加工资源不变。
4)分别计算P和Q的总成本S和T。
5)如果S>T,则令P=Q,否则不保留Q。
6)随机生成两个切点l1和l2,同时令R=P。
7)对R的两个切点l1和l2之间的加工序列对应的加工资源执行以下步骤。
a)生成随机数r,若r<0.5,则不改变当前工序的加工资源,否则执行下一步。
b)随机选择候选资源中的加工资源替换当前工序的加工资源。
8)得到P的子代R,再计算P和R的总成本S和Y。
9)如果S>Y,则令P=R,否则不保留R。
2.3 GCGA 的流程
贪婪元胞遗传算法(GCGA)在二维空间中对染色体进行遗传操作,即将种群中的每个染色体放置在一个二维网格中,然后对每一个染色体及其最优的邻居染色体进行交叉和变异操作。在元胞自动机模型中,常用的2 维元胞自动机的邻居类型有:von Neumann 型、Moore 型以及扩展的Moore 型[21],如图3所示。本文所使用的邻居类型为Moore 型,一共有8个邻居。

图3 2 维元胞自动机的邻居类型
图4 为GCGA 算法的流程图,其具体步骤如下:

图4 GCGA 算法的流程图
1)输入加工工序的优先矩阵及其候选加工资源,可选机床的成本、可选刀具的成本、机床、刀具和装夹变换一次的成本,交叉概率和变异概率,种群规模和最大迭代次数。
2)初始化种群中染色体的FOS。
3)初始化FOS 的加工资源。
4)计算种群中每个染色体的总成本。
5)当迭代次数小于最大迭代次数时,执行以下步骤:
a)对种群中的每一个染色体,选择其最优的邻居染色体组成母体。
b)生成随机数,如果随机数小于交叉概率,则对母体的FOS 执行交叉操作。同时对母体的FOS 的加工资源执行交叉操作。
c)生成随机数,如果随机数小于变异概率,则对母体执行变异操作。
d)计算当前种群最优染色体并保存。
3 实验分析
3.1 实验参数
为验证GCGA 的优化性能,实验采用文献[4]及文献[9-14]共同使用的案例ANC-101。ANC-101为具有20 个加工工序的工序排序优化问题,其工序优先关系如图1 所示,机床资源如表6 所示,刀具资源如表7 所示,特征和操作信息如表8 所示。机床、装夹和刀具变换一次的成本分别为160、100 和20,5 种成本的权值均为1。根据文献[4]和文献[9-14]使用的种群规模和最大迭代次数,把种群规模设置为144,最大迭代次数设置为200。实验独立重复进行10 次。

表6 机床信息

表7 刀具信息

表8 ANC-101 的特征、操作、TADS 和制造资源
实验条件:MATLAB 2018b,处理器为Intel(R)Core(TM) i7-10510U CPU @1.80 GHz 2.30 GHz,内存为12 G。
3.2 实验结果及分析
经过10 次独立重复实验,得到如下实验结果:在10 次独立重复实验中,每一次均能得到最优值2530,表5 为其得到的最优方案,并且最早收敛代数为9,图5 为其进化曲线。由此可见,GCGA 算法具有较高的稳定性。

图5 进化曲线
为了验证GCGA 算法的优化性能,将GCGA 算法与文献[4]提出的ESGA 算法、文献[9]提出的混合遗传算法和模拟退火算法、文献[10]提出的混合图遗传算法、文献[11]提出的TSGA 算法、文献[12]提出的FOSOGA 算法、文献[13]提出的PSO 算法和文献[14]提出的ACO 算法等7 种算法进行对比,10 次独立重复实验得到的总成本的最优值、最差值、平均值和最早收敛代数的对比结果如表9 所示。
由表9 可以看出:在上述8 种算法中,只有文献[4]提出的ESGA 算法、文献[12]提出的FOSOGA 算法、文献[14]提出的ACO 算法和本文提出的GCGA算法获得了最优值2530,其余的算法获得的最优值都较大。并且,本文提出的算法获得的平均值和最差值都优于其余的7 种算法。同时,在10 次独立重复实验中,最早收敛代数为9,比文献[12]提出的FOSO⁃GA 的最早收敛代数38 要早。

表9 8 种算法的计算结果
实验数据结果充分表明:GCGA 算法在求解工序排序优化时具有较高的稳定性、收敛速度及收敛精度。
4 结论
为了解决CAPP 中的工序排序优化问题,本文提出贪婪元胞遗传算法(GCGA)。该算法在元胞遗传算法的基础上,引入元胞自动机的Moore 型邻域结构避免陷入局部最优;利用优先矩阵实现拓扑排序算法,确保初始种群中每个染色体的加工顺序满足优先关系的约束;引入贪婪算法生成初始种群的加工资源,提高初始方案的质量;设计结合精英个体保留策略的交叉算子和变异算子,保证解空间在迭代过程中的可行性。GCGA 算法能够有效解决工序排序优化问题,能为实际工业生产提供丰富的理论指导。

