含空间自回归误差的空间自回归模型的经验欧氏似然推断*

唐 洁

（广西师范大学数学与统计学院，广西桂林541004）

0 引言

含空间自回归误差的空间自回归模型(Spatial Autoregressive Model with Spatial Autoregressive Disturbanc⁃es，简记为SARAR):

其中，n是空间样本数量；ρj,j=1,2 是空间自回归系数且|ρj| ＜1,j=1,2；βk×1是相应回归系数向量；Xn=(x1,x2,…,xn)′是n×k数据矩阵,包括k列解释变量；Yn=(y1,y2,…,yn)′是n×1 维被解释变量;Wn和Mn是已知的n×n空间权重矩阵（非随机）；ϵ(n)是空间误差模型n×1 的误差向量

SARAR 模型是更一般的空间计量模型，它对存在空间依赖性的数据有较好的解释作用，无论是滞后项存在依赖性还是扰动项存在空间依赖性。它将存在空间误差效应的空间误差模型(SEM)与空间滞后效应的空间自回归模型(SAR)结合起来，分别对应于ρ1=0 与ρ2=0 的情形。

经验似然方法是由Owen 在文献[1]中提出的一种参数推断方法。通过经验似然方法研究SARAR 模型则是文献[2]的主要工作。但是经验似然方法在求解过程中会出现没有显示解的情况，且计算复杂。为了解决这些问题，Owen 在文献[3]中提出用经验欧氏似然来代替经验似然。而罗旭在文献[4]中，就系统地研究了经验欧氏似然，发现了可以很好地解决经验似然中的棘手问题，并且经验欧氏似然也同样拥有大样本性质。基于此，本文通过经验欧氏似然方法来研究SARAR 模型。

1 主要结果和证明

记An(ρ1) =In-ρ1Wn,Bn(ρ2) =In-ρ2Mn并且假设An(ρ1)和Bn(ρ2)是非奇异矩阵。于是可以得到：

此时，假设ϵ(n)是正态分布的，则Yn服从期望为An1(ρ1)Xn β，方差为的正态分布。

于是，Yn的拟似然函数为：

其中ϵ(n)=Bn(ρ2){An(ρ1)Yn-Xn β}。

进而，Yn的拟对数似然函数为：

令上述偏导数等于0，可以获得以下估计方程：

则Fi-1⊆Fi，是Fi-可测的，并且E(|Fi-1) =0。因此，{,Fi,1≤i≤n}和{,Fi,1≤i≤n}构成两个鞅差序列，且

根据(2)到(7)可以得出参数θ≜(β′,ρ1,ρ2,σ2) ∈Rk+3的估计方程，令

通过ωi(θ)提出θ的经验欧氏似然比统计量

其中，{pi}满足

在本文中，记μj=E(ϵji),j=3,4，用Vec(diagA)表示由矩阵A的对角线上的元素构成的列向量，用‖a‖表示向量a的第二范数，用1n表示由1 作为元素组成的n维列向量，为了获得经验欧氏似然比统计量的渐近分布，需要给出以下假设条件：

A1.{ϵi,1≤i≤n}是均值为0，方差有限的独立同分布随机变量序列，且存在η1＞0，使E|ϵ1|4+η1＜∞。

A2.假设Wn,Mn,A-1n(ρ1),B-1n(ρ2)及{xi}满足以下条件：

（i）矩阵Wn，Mn，A-1n(ρ1)，B-1n(ρ2)行元素和列元素的绝对值之和均一致有界；

（ii）{xi}是一致有界的。

A3.存 在常数cj＞0,j=1,2,使 得0 ＜c1≤λmin(n-1c) ≤λmax(n-1Σk+3) ≤c2＜∞,其 中λmin(A)和λmax(A)分别表示矩阵A的最小和最大的特征值，且

其中，

引理1在(A1)～(A3)假设条件下，当n→∞时，有

见文献[4]的引理3。

定理1在(A1)～(A3)假设条件下及模型(1)下，当n→∞时，有-2Ln(θ)→dχ2k+3，其中，表示自由度为k+3 的卡方分布。

证明：SARAR 模型下经验欧氏（对数）似然函数为：

利用拉格朗日乘子法给出Ln(θ)的表达式。为此取

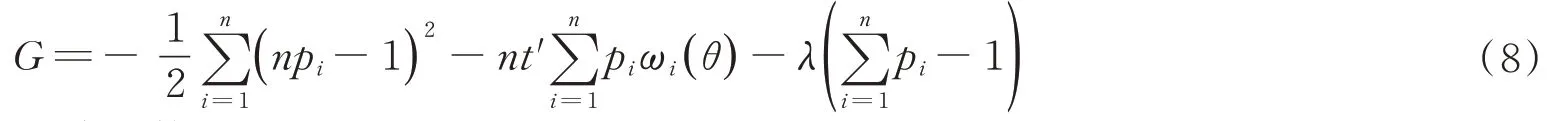
其中t′∈Rk+3。对G求关于pi的偏导数，得

并令

在(9)式两边对i从1 加到n求和，得

上式化简可得

由(10)～(12)可得

由引理1，得

由此完成了定理1 的证明。