考虑随机共因失效的战时合成部队任务成功概率
王双川, 贾希胜, 胡起伟, 曹文斌, 郭驰名
(1.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003; 2.中国人民武装警察部队指挥学院 勤务保障系, 天津 300100)
0 引言
合成部队是陆军编制体制调整改革中组建的新型部队和主要作战力量,其相关课题是新形势下陆军研究的热点。战时装备维修保障是短时间内恢复装备战斗能力、确保部队持续作战的必要手段,对于战斗成败具有直接影响,其核心和根本是提高装备任务成功概率。任务成功概率是在规定条件下和规定任务剖面内,武器装备完成规定任务的概率[1],是评估装备维修保障效能的重要指标。因此,战时合成部队任务成功概率评估是战时衡量合成部队完成任务能力、优化合成部队装备维修保障方案的有效方法。
国内外学者对装备任务成功概率评估问题开展了许多卓有成效的研究工作[2-3]。文献[4-6]分别以部件、装备功能单元和单台装备为研究对象,采用解析或仿真的方法对其任务成功概率进行评估;文献[7]利用基于半马尔可夫系统的矩阵积分方程,对具有时间冗余的系统任务成功概率进行评估;文献[8]建立了k/n系统任务成功标准的静态模型和动态模型,并根据有限马尔可夫链嵌入法得到了两种模型的不同状态空间和转移概率矩阵;文献[9]基于生灭过程研究了给定维修保障方案下复杂系统的任务成功概率;文献[10]基于集值随机过程建立了可修多状态两阶段任务系统任务成功性评估模型;文献[11]建立了基于扩展的面向对象Petri网的多阶段任务系统(PMS)任务成功概率评估模型;文献[12]基于多值决策图模型和马尔可夫模型,对多状态PMS任务成功性进行评估;文献[13]考虑备件数量和维修能力,在分析各阶段任务之间逻辑关系的基础上,评估可修PMS任务成功概率;文献[14]给出了一个基于全概率定律和条件概率的递推公式,对不完全故障覆盖条件下k值和部件故障时间分布随阶段变化的k/n系统任务成功概率进行评估;此外,文献[15]研究了舰载机执行着舰任务时的成功概率;文献[16]考虑组合阶段需求和部件的可修性,基于系统行为模型和连续时间马尔可夫链对PMS任务成功性进行分析;文献[17]认为装备任务成功概率近似等于装备备件短缺数满足任务成功要求的概率,并据此建立了作战单元任务成功性评估模型;文献[18]描述并分析了装备体系任务流程,然后通过离散事件仿真分析了装备体系任务成功性;文献[19]针对动态k/n结构系统,利用多值决策图对其任务成功概率进行评估;文献[20-21]分别基于蒙特卡洛仿真和二元决策图方法,评估随机共因失效(RCCF)事件发生情况下装备任务成功性;文献[22]建立了一种用于任务时间冗余情况下PMS任务成功概率评估的Petri网仿真模型;文献[23]融合系统多阶段运行数据,利用动态贝叶斯网络方法评估了系统任务成功概率。综合来看,现有研究成果主要有以下3个特点:1)对平时任务成功性评估问题研究较多,对战时任务成功性评估问题研究较少;2)对装备关键部件、装备子系统和单台装备任务成功性评估问题研究较多,而对复杂武器系统、作战单元或建制部队任务成功性评估问题关注较少;3)建模时常假设一次系统停机只有一个部件失效、换件修理时间忽略不计等,与实际情况不符。
因此,本论文针对合成部队作战任务,考虑装备共因失效(CCF)和换件修理时间,对战时合成部队任务成功性进行评估。同时,鉴于合成部队装备的多样性、合成部队多作战单元协同作战任务的复杂性、RCCF事件到达时间和作战任务持续时间的随机性等,建立战时合成部队任务成功概率评估的解析模型困难较大,而仿真方法具有强大的行为建模能力且比较容易实现,本文采用蒙特卡洛方法对合成部队作战任务成功概率进行仿真评估。
1 战时合成部队任务成功概率评估的理论基础
1.1 合成部队装备层次结构分析
合成部队装备内容和层次分析是构建合成部队作战任务剖面、分析合成部队装备CCF及其维修保障特点的前提。在总体层次上,按照合成部队编制,合成部队编配有坦克、步战车、装甲输送车、火箭炮、榴弹炮、地空导弹车、工程防化装备、电子对抗装备等多种类型的装备,表现出品种全、数量多的显著特征。在具体装备层次上,从装备结构角度,合成部队装备可划分为多个子系统,包括底盘系统、液压系统、电气系统、炮控系统、火控系统、指挥通信系统等(不同类别的装备主要功能不同,因此,所含的装备子系统可能存在差异)。在装备子系统层次上,各子系统由多个部件构成且可以有多种结构,如串联结构、并联结构、混联结构、表决结构等。综上所述,合成部队装备层次结构如图1所示。
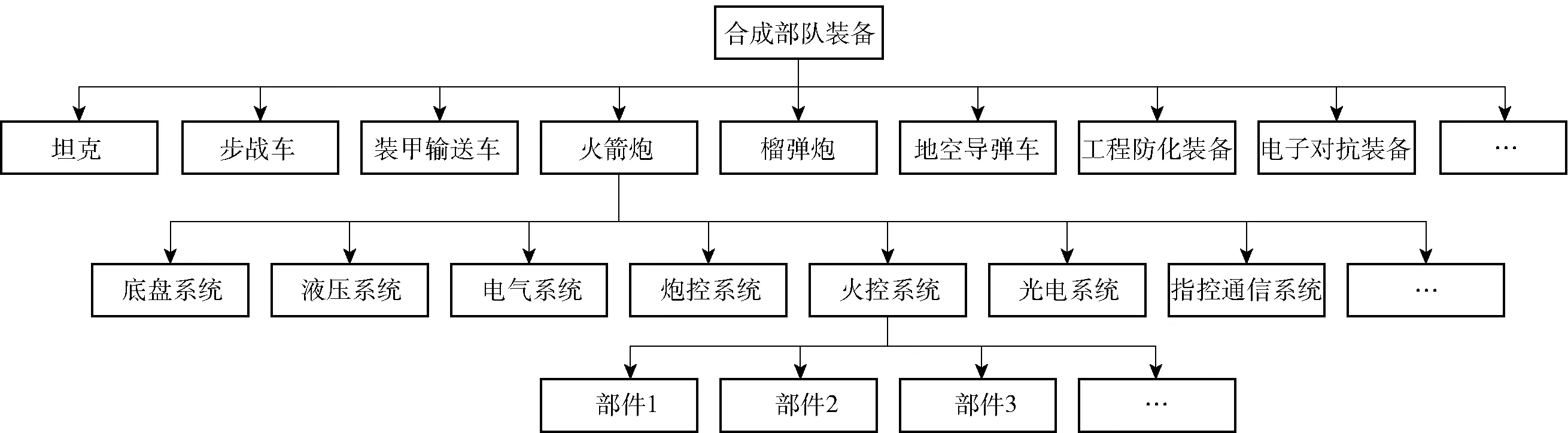
图1 合成部队装备层次结构Fig.1 Hierarchical structure of equipment of synthetic forces
1.2 合成部队作战任务剖面构建
合成部队是由多类型作战单元综合集成的有机整体,各作战单元之间的主要任务、主战装备、部署位置、任务环境等各不相同,因此,合成部队任务的成功完成需要多个作战单元的协同、配合。可见,战时合成部队任务成功概率评估本质上是对合成部队多作战单元协同作战任务成功概率进行评估。其中,作战单元是指能在一定范围内独立遂行作战任务的作战单位,主要包括作战装备及其保障系统等。这里以2个作战单元(分别为CU1和CU2)为例,说明合成部队多作战单元协同作战任务剖面,如图2所示。图2中,CU1中的作战装备是由n1台EQ1装备构成的装备群(表示为EQG1)和n2台EQ2装备构成的装备群(表示为EQG2),CU2中的作战装备是由n3台EQ3装备构成的装备群(表示为EQG3)。
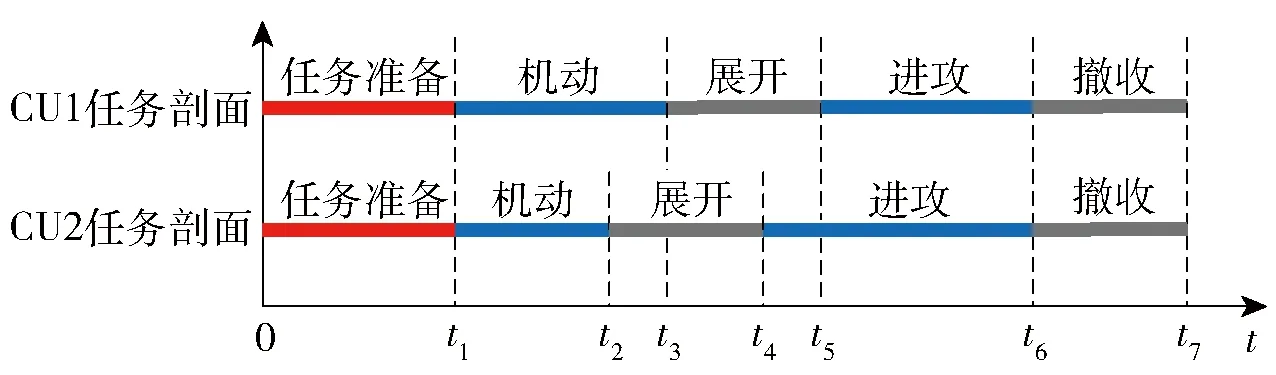
图2 合成部队作战任务剖面示例Fig.2 An example of combat mission profile for synthetic forces
1.3 合成部队装备CCF和维修保障特点分析
分析战时合成部队装备CCF及其维修保障特点,是为解决战时合成部队任务成功性评估问题进行合理假设和建模的前提。敌方火力打击是战时装备损伤的主要来源,且常常导致装备系统中多个部件同时失效,因此, CCF是战时合成部队装备丧失战斗能力的主要因素。所谓CCF,是指系统内多个部(组)件在同一时刻由于共同原因所导致的失效[24],而导致CCF的事件称为CCF事件。因此,敌方火力打击是一类典型的CCF事件。易知,交战过程中敌方火力打击的时刻、次数都是随机的,所以合成部队装备CCF的时刻和次数也是随机的。文献[20-21,25-27]将这类具有随机性的CCF称为RCCF,将具有随机性的CCF事件称为RCCF事件。此外,根据装备实装实打试验数据[28],装备在遭受火力打击时,会以一定的概率造成装备系统内部件失效,且各部件失效的概率有所不同。综上所述,对战时合成部队任务成功性进行评估,应当充分考虑合成部队装备CCF的随机性、不确定性及其产生的影响。
在新的维修体制下,合成部队装备维修保障具备以下2大特征:一方面,合成部队装备维修保障是按照装备子系统划分分别展开实施的,对应地,将合成部队装备维修保障人员按照装备子系统类别进行编组;另一方面,合成部队装备维修保障属于部队级维修范围,主要通过换件修理对待修装备实施修复。
2 问题描述与假设
以图2所示的合成部队进攻阶段任务为研究对象,开展战时合成部队任务成功性评估问题研究。设该阶段任务中,合成部队任务的成功要求是任意时刻至少保持r1台EQ1装备、r2台EQ2装备和r3台EQ3装备均处于完好状态,若一类或多类装备的完好数量低于所设阈值时,只要在允许抢修时间ta内通过维修保障使得完好状态装备的数量恢复到阈值水平,则认为任务仍然能够成功,求该合成部队成功完成进攻阶段任务的概率。
为有效开展研究,本文结合作战任务模型,作出如下假设:
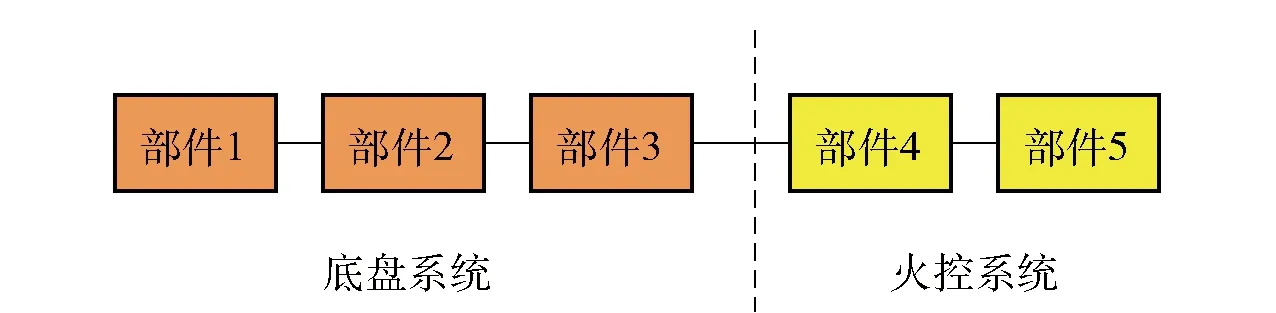
1)完成该阶段作战任务需要各装备的底盘系统和火控系统同时工作;
2)单台装备只有损伤和完好两种状态,且在进攻阶段开始时各个装备均处于完好状态;
3)CU1进攻阶段任务时间(图2中的t5时刻至t6时刻)服从参数为λm的指数分布,CU2任务开始时刻早于CU1任务开始时刻Δt(CU2任务时间是图2中的t4时刻至t5时刻);
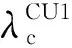
5)部件失效后立即换件修理,修理时间均服从对数正态分布,且维修时装备不受RCCF事件影响;
6)除备件外,合成部队其他维修保障资源均满足需求。
3 战时合成部队任务成功概率仿真评估
针对第2节描述的问题,可以采用蒙特卡洛仿真方法对合成部队多作战单元协同作战任务成功概率进行评估,步骤如下:
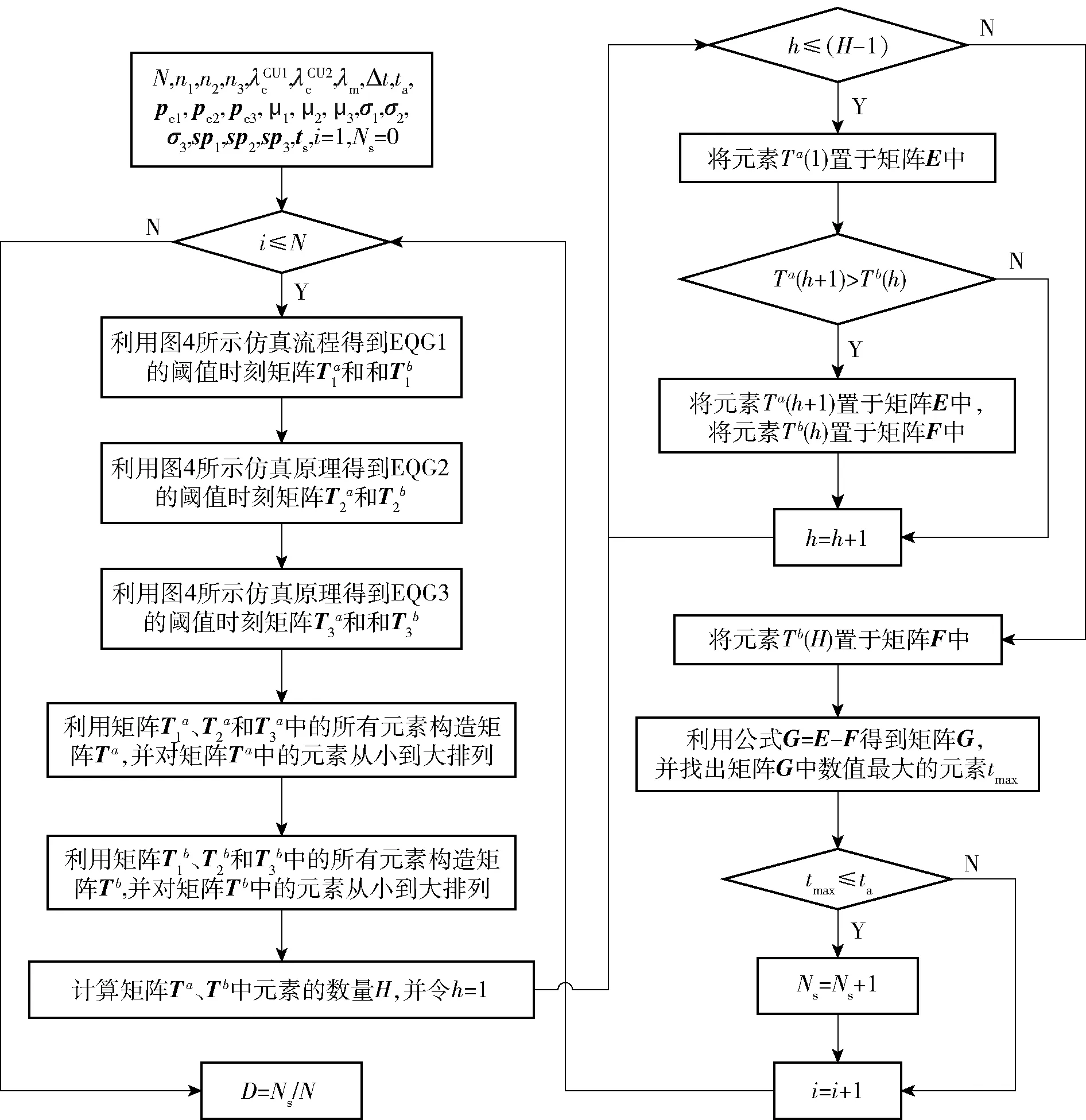
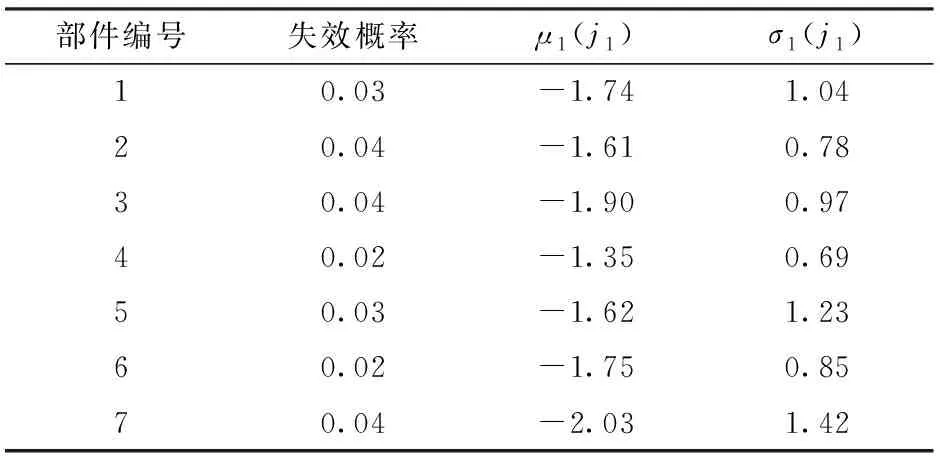
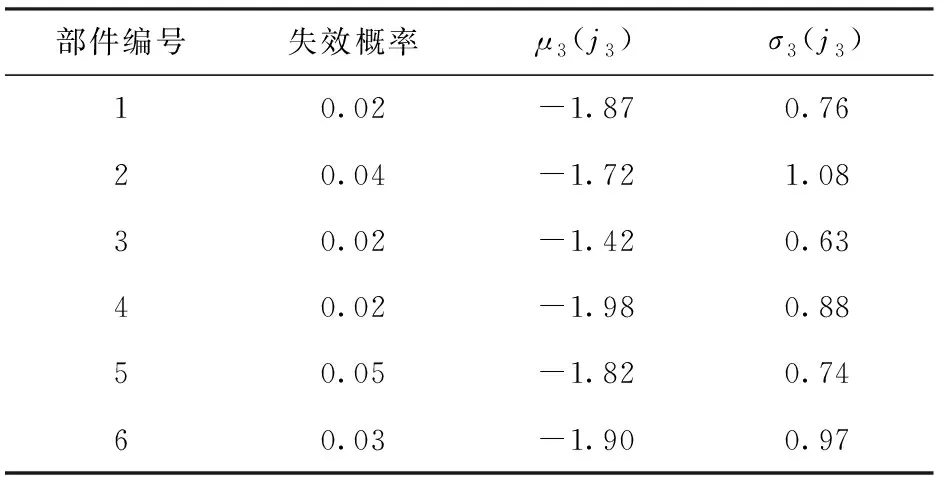
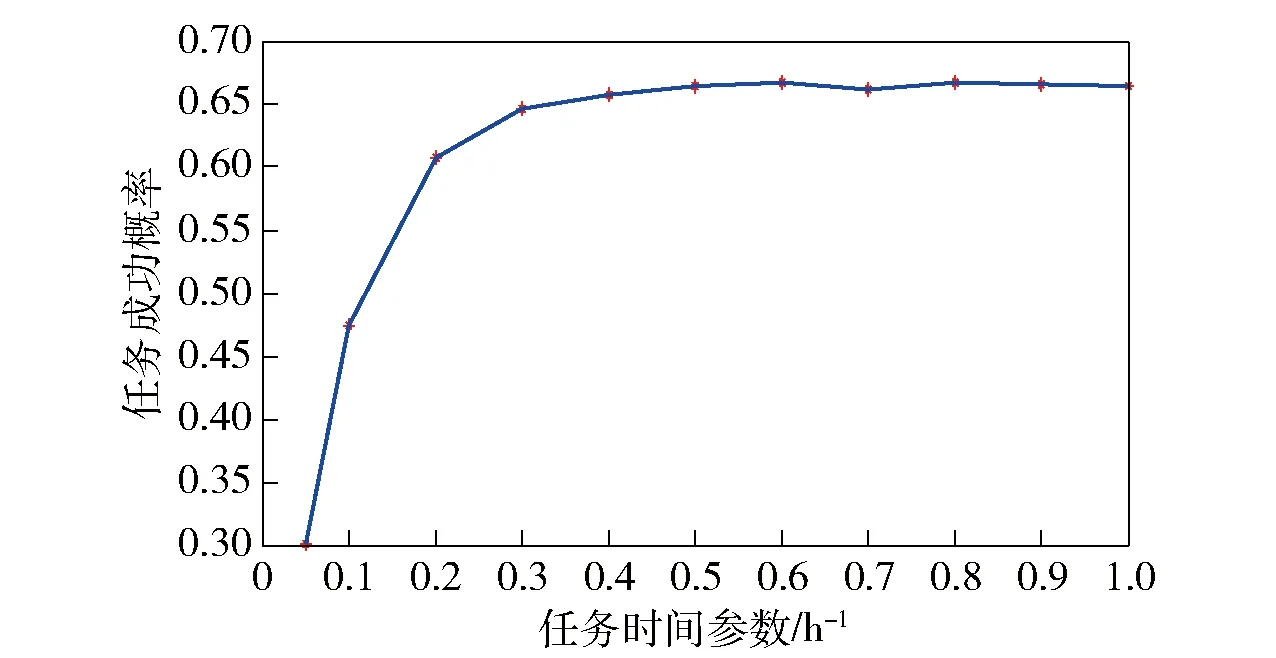
步骤1通过仿真方法,计算任务时间内各个时刻EQG1中处于完好状态的装备数量,并记录其“开始 步骤2根据合成部队装备任务成功要求,首先找出所有阈值时刻中开始不满足合成部队任务成功要求的所有时刻,构造矩阵E,之后,从所有阈值时刻中找出开始满足合成部队任务成功要求的所有时刻,得到矩阵F; 步骤3令G=F-E,并找出矩阵G中数值最大的元素tmax; 步骤4给定合成部队任务允许抢修时间ta,比较ta和tmax的大小关系,若tmax≤ta,则合成部队任务成功; 步骤5按照设置的仿真次数,重复执行步骤1~步骤4,并记录总任务成功次数,继而得到合成部队任务成功概率。 需要说明的是,“开始 根据步骤1所述,本节以EQG1为例,说明装备群阈值时刻的计算流程。当仿真次数为i时,为便于计算,不妨设CU2进攻阶段任务开始时刻为0 h,CU1进攻阶段任务时间为tm(tm为根据参数λm随机产生的进攻阶段任务时间),则CU1进攻阶段任务开始时刻为Δt,结束时刻为(tm+Δt)。EQG1阈值时刻仿真计算流程如图3所示,具体步骤为: 1)输入相关参数,具体包括:CU1任务开始时刻Δt、EQ1装备数量n1、RCCF事件到达CU1的时间间隔参数λc1、任务时间tm、RCCF条件下EQ1装备各部件的失效概率矩阵pc1(EQ1装备中部件数量为κ1,编号k1=1,2,…,κ1,其中:底盘系统部件数量为κc1,编号为1,2,…,κc1;火控系统部件数量为κf1,编号为κc1+1,κc1+2,…,κc1+κf1;显然,κ1=κc1+κf1)、各部件失效后换件修理时间参数矩阵μ1和σ1、备件携行量矩阵sp1,并将仿真时钟ts1的初始值设为元素均为Δt的1×n1矩阵(即任务开始时刻装备j1(j1=1,2,…,n1)的当前仿真时钟ts1(j1)=Δt)。 图3 EQG1阈值时刻确定仿真流程Fig.3 Simulation flow to determine critical moments of equipment group 1(EQG1) 3)若w1≤y1,则建立零矩阵tr1=(0)n1×κ1,之后,令j1=1,并执行第4步,否则,跳转至第10步。 4)若j1≤n1,则执行第5步,否则,令w1=w1+1,并执行第3步。 5)比较第w1次RCCF事件达到的时刻tc1(w1)与装备j1的当前仿真时钟ts1(j1)的大小,若ts1(j1)≥tc1(w1),则ts1(j1)的值保持不变,若ts1(j1) 6)基于装备系统结构函数判断装备j1状态,若装备j1完好,记其状态Y1(j1)=1,然后,令j1=j1+1,并跳转至第4步,否则,记ts1(j1)为装备j1的损伤时刻,并将ts1(j1)的值置于stf1中,然后执行第7步。 7)记装备j1中未失效部件k1的维修时间tr1(j1,k1)=0;对于失效的部件k1,若其备件库存量sp1(k1)>0,则随机生成维修时间tr1(j1,k1),同时,部件k1的备件库存量sp1(k1)=sp1(k1)-1,若失效部件k1库存量为0,则将该部件维修时间记为tr1(j1,k1)=-1. 8)统计矩阵tr1第j1行元素中“-1”的数量m1,如果m1>0,则表示本次RCCF事件造成装备损伤后备件出现短缺,此时,令装备j1当前时钟ts1(j1)=tm+Δt+1,并将ts1(j1)的值置于str1中;如果m1=0,则表示本次RCCF事件造成装备损伤后储备备件充足,此时,执行第9步。 10)将stf1和str1中元素由小至大排序,之后,在区间[Δt,tm+Δt]内以0.01 h为步长,统计各时刻完好装备数量,可得矩阵Re1(易得,Re1中共有q1=tm/0.01+1个元素)。 图4 战时合成部队任务成功概率仿真评估流程Fig.4 Evaluation flow of mission success probability based on simulation during wartime 在已知各装备群阈值时刻的基础上,依据步骤2~步骤5所述过程,基于蒙特卡洛仿真方法的战时合成部队任务成功概率评估过程如图4所示,具体仿真过程为: 2)若i≤N,则执行第3步,否则,跳转至第12步。 5)统计Ta、Tb中元素的个数H,并用Ta(h)、Tb(h)分别表示Ta、Tb中的第h个元素,令h=1. 6)若h≤(H-1),则将元素Ta(1)置于矩阵E中,然后,执行第7步,否则,将元素Tb(H)置于矩阵F中,然后,跳转至第9步。 7)若Ta(h+1)≥Tb(h),则将元素Ta(h+1)置于矩阵E中,将元素Tb(h)置于矩阵F中,并执行第8步,否则,直接执行第8步。 8)h=h+1,跳转至第6步。 9)令G=F-E,找出矩阵G中数值最大的元素tmax. 10)若tmax≤ta,则本次任务成功,即Ns=Ns+1,并执行第11步,否则,直接执行第11步。 11)i=i+1,跳转至第2步。 12)利用公式D=Ns/N,计算合成部队任务成功概率。 图5 进攻阶段EQ1装备结构Fig.5 Structure of an EQ1 equipment during attack phase 图6 进攻阶段EQ2装备结构Fig.6 Structure of an EQ2 equipment during attack phase 图7 进攻阶段EQ3装备结构Fig.7 Structure of an EQ3 equipment during attack phase RCCF条件下EQ1装备、EQ2装备、EQ3装备各部件的失效概率及失效后的换件修理时间参数分别如表1、表2、表3所示。 任意给定备件携行方案,如EQ1装备的备件携行量sp1=(6,7,6,5,6,5,7)、EQ2装备的备件携行量sp2=(7,6,8,6,5)、EQ3装备的备件携行量sp3=(5,7,6,4,7,6)。此时,使用MATLAB软件,基于图3、图4给出的仿真流程进行编程,可以得到战时合成部队任务成功概率D=0.610. 可见,利用本文模型可以对合成部队多作战单元协同作战任务成功概率进行评估,验证了模型的可用性和有效性。 表1 RCCF条件下EQ1装备各部件的失效概率和修理时间参数 表2 RCCF条件下EQ2装备各部件的失效概率和修理时间参数 表3 RCCF条件下EQ3装备各部件的失效概率和修理时间参数 为了探究战时合成部队任务成功概率与任务时间的关系,基于上述备件携行方案,分别计算任务时间参数λm取不同值时的战时合成部队任务成功概率D,得出D随λm的变化关系,如图8所示。 图8 任务时间与战时合成部队任务成功概率的关系Fig.8 Relationship between mission time and mission success probability of the synthetic forces during wartime 由图8可知,在给定备件携行方案下,随着λm的增加(即进攻阶段任务时间的减少),战时合成部队任务成功概率呈增长态势,但当λm≥0.2时,即进攻阶段平均时间小于5 h时,战时合成部队任务成功概率变化幅度不大。因此,在sp1=(6,7,6,5,6,5,7)、sp2=(7,6,8,6,5)、sp3=(5,7,6,4,7,6)的备件携行方案下,为取得战争胜利,应尽可能将进攻阶段任务时间控制在5 h以内。可见,本文模型亦可用于给定备件携行方案下作战任务时间的优化。 任意调整各类装备的备件携行量,对合成部队进攻阶段任务成功概率进行评估。例如,当各类装备的备件携行量均增加3时(此时,sp1=(9,10,9,8,9,8,10)、sp2=(10,9,11,9,8)、sp3=(8,10,9,7,10,9)),可得战时合成部队任务成功概率D=0.706. 可见,各类备件的携行数量对战时合成部队任务成功概率具有直接影响。因此,在本文评估模型的基础上,可以以最大化战时合成部队任务成功概率为目标,进一步研究战时合成部队备件携行方案的优化问题,从而为战时合成部队携行备件的优化配置提供决策依据。 本文以陆军新调整组建的合成部队为研究对象,分析了合成部队装备及其维修保障特点,建立了合成部队作战任务剖面,提出了战时合成部队进攻阶段任务成功要求,然后,采用仿真方法研究了给定备件携行方案、考虑换件修理时间以及敌方火力打击服从指数分布等情况下的合成部队进攻阶段任务成功概率评估问题,并通过算例分析验证了提出方法的可用性及有效性,为评估战时合成部队任务成功概率提供了一种有效方法和思路,对于合成部队建模和多作战单元任务成功概率评估具有一定的借鉴意义。下一步,在本文研究基础上可以从以下2个方面进行拓展研究:1)开展进攻阶段合成部队备件携行量优化模型及算法研究;2)分析机动、展开、撤收阶段的任务特点,采用有效方法对战时合成部队多阶段任务成功概率进行科学评估。3.1 各装备群阈值时刻仿真计算

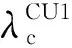
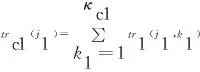

3.2 合成部队任务成功概率评估

4 算例分析
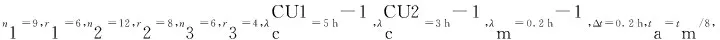



5 结论

