基于样本冗余度的主动学习优化方法

范纯龙 王翼新 宿 彤 张振鑫

1(沈阳航空航天大学计算机学院 辽宁 沈阳 110136) 2(辽宁省大规模分布式系统实验室 辽宁 沈阳 110136)

0 引 言

近几年，图像识别及其分类是深度学习领域中的重要应用，其中有监督学习是重要方法之一。但是利用该方法解决图像分类问题需要大量的有标签数据，然后利用分类器的参数学习样本中的特征，从而达到较好的分类效果。对于大量有标签数据的需求，网络技术的普遍应用可以使人们很容易获得海量数据，但是在一些实际应用中[1-3]，取得无标签样本很容易而标注样本是代价昂贵或耗费时间的。基于此类常见的问题，Angluin[1]提出了“主动学习”。

主动学习的目的是减少对样本数据的标注成本，用最少的有标签样本达到接近全样本训练效果。主动学习按照样本抽样模式可分为流样本模式和池样本模式，由于流样本模式的选择策略需要根据不同的任务进行适当的调整，很难作为通用方法使用。所以，近些年来主动学习主要在池样本模式上发展[4-6]，即在固定的大量无标签样本集中，根据选择策略反复选择对当前分类器而言信息量大的样本，其中按照选择策略原理不同，主要有基于不确定度[3,5,7-8]、泛化能力[9-10]、模型空间[11-12]等方法。这些策略都是根据样本与当前分类器或样本分布之间的关系，每次选择的样本数量多、信息量大且训练效果明显，但是没有考虑到样本对分类器而言信息重叠问题，即信息冗余问题。尽管每次选择样本的信息量足够大，但是信息冗余问题会导致选择多余的无意义样本，主动学习会因此失去意义。

主动学习的分类器选择主要有SVM[5,7,13]、神经网络[3,8-9,14]和KNN分类器[15]。为了解决选择样本信息冗余问题，很多学者在以SVM为分类器的基础上做了很多研究[13,16-17]，提出了样本相似性、代表性等概念解决了该问题。但是这些方法在计算这些指标时的计算量很大，且在多分类时训练分类器个数较多，实用性不高。进一步地，有学者提出将神经网络作为分类器，神经网络有能同时进行多分类且分类效果好的优点。目前方法主要考虑如何更准确度量样本不确定性，利用不确定性选择分类边界附近样本，并将之作为信息量大的样本。在解决信息冗余问题上，由于神经网络没有明确的可解释性，除了可视化方法外，无法明确地判断样本对神经网络的信息具体是什么，所以目前方法考虑更好地度量样本对分类器的不确定性[3,8-9,14,18]，没有考虑冗余问题。

综上所述，SVM在计算量大、样本类别多的情况下训练麻烦，在以神经网络为分类器条件下没有解决多个样本之间信息冗余问题。针对此问题，提出DRAL(Discriminative And Redundancy Active Learning)方法，该方法用带有多层感知机(multi-layer perception，MLP)的卷积神经网络CNN计算得到样本潜变量向量表示样本信息，用不确定性方法选择信息量大的样本构成候选集，利用余弦距离从候选集选出信息量大且冗余度小的样本集。不确定性方法经过该方法提升后，在LeNet-5和NIN(Network in Network)[19]神经网络上，用Mnist、Fashion-mnist和Cifar-10数据集测试，在相同准确率条件下，最低减少11%标记样本。

本文的主要贡献在于：通过利用神经网络计算的潜变量，在度量样本信息量基础上提出一种降低样本冗余度方法。

1 相关工作

样本选择策略是主动学习过程中的核心问题，在池样本模式下，根据不同分类器有不同选择策略。

以SVM为分类器条件下，利用样本与支持向量之间的距离明确地度量了样本的信息量，例如SVM的批模式主动学习方法等[20-22]，但是考虑到样本之间分布问题,使用最大均值差异(Maximum Mean Discrepancy,MMD)[23]度量了样本集之间的分布差异，从而保证了无标签集和有标签集的分布一致性，例如边缘分布批模式方法(Batch Mode Active Learning,BMAL)[13]、代表性方法(Discriminative and Representative Model Active Learning,DRMAL)[16]。进一步地，使用相似度稀疏模型(Dissimilarity-based Sparse Modeling Representative Selection,DSMRS)[24]和互信息方法度量了样本集之间相似性从而降低了样本集之间的冗余性。例如自适应主动学习方法[15]、凸规划主动学习方法(Convex Programming Active Learning,CPAL)[25]等。

以神经网络为分类器条件下，与SVM类似，越接近分类边界的样本信息量越大，目前大多数采用不确定性方法度量。由于神经网络未能明确解释原因，有些学者认为当前方法选择样本不够接近分类边界，需要重新选择在分类边界附近的样本，例如：计算多次dropout后的结果均值作为最终分类结果的贝叶斯算法(Deep Bayesian Active Learning, DBAL)[8]；利用生成对抗样本的Deepfool算法[26]攻击无标记样本(Deep Fool Active Learning, DFAL)算法；考虑到样本分布关系，为了保证有标记样本集和无标记样本集的分布一致性，利用加入了分类器自定标签的高可信样本方法(Cost-Effective Active Learning,CEAL)[27]，用欧氏距离把样本选择问题变成K中心问题[9]，这些方法都保证了分布一致性且可以选择信息量大且数量多的样本，但是没有解决信息冗余问题。本文提出DRAL方法降低了冗余度，达到更好的效果。

2 问题描述

本节定义了主动学习问题，通过带有MLP的CNN中的“潜变量”间接度量了样本信息量和样本信息冗余度。结合主动学习过程，定义了最小化冗余度问题。

假设有m类n个样本。基于池样本选择样本模式的主动学习问题如下：

问题1假设有标记集样本数量为nL，L={xi|i=1,2,…,nL}；无标记集样本数量为nU，U={xi|i=1,2,…,nU}，xi∈Rk且nL+nU=n；样本标签集：Y={yi|i=1,2,…,nL}且yi∈Rm。CNN模型的损失函数为l(L,Y;f(θ))，其映射为RnL×k×RnL×m→RnL。每次从U中选择k个样本构成Si集放入到L中，主动学习问题为：

minLE[l(L,Y;f(θ))]-E[l(L+U;f(θ))]

其中损失函数是信息交叉熵函数，即：

(1)

式中：T是迭代次数;1{·}是指示函数，当CNN预测正确时为1，否则为0；p(yi=j|xi；θ)是经过Softmax过程后在j类的输出结果。

由于CNN没有明确的可解释性，所以明确样本对CNN的具体信息是什么很困难。鉴于此问题，假定CNN经过卷积层后接有MLP全连接层，并规定MLP中的隐层输出向量为潜变量，通过潜变量抽象表示样本信息。潜变量向量的模长表示信息量，通过计算样本间距离大小表示信息冗余。常用距离度量有欧氏距离和余弦距离，余弦距离计算效果更好且计算得出结论相同，所以选择余弦距离。进一步地，内积度量样本间的信息冗余度，即内积越大表示潜变量的相似度越高，被比较的两个样本间的信息量冗余度越高。

I=[I1,I2,…,In]

为了解决问题1，通过降低冗余度达到该目的，即选择信息量大且冗余度小的样本集。问题1变为如何选择样本集Si，使得样本间冗余度最小。

问题2假设已有冗余度矩阵R，从U中选择样本集Si，使得R的均值最小，即：

minLaverage(R)

3 冗余度方法

冗余问题主要在多次选择的Si样本集之间或者单次选择的Si集中样本之间。假设每次选择完Si，经过标记后CNN在集合L上收敛，因此，每次迭代选择的Si样本集之间信息冗余少，冗余问题主要在Si集中的样本之间。

图1 si集的冗余度问题分析情况

3.1 不确定性方法

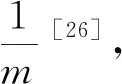
(1) 低可信度[26]:

x*=argmaxx[1-p(ymax|xi;θ)]

(2)

式中：ymax=max(yi=j|xi;θ)。样本在各个分类概率中的最大值由小到大排序，选择前K个样本。

(2) 信息熵[26]:

(3)

按照信息熵由大到小排序，选择前K个样本。

(3) 贝叶斯估计[8]:

(4)

在多次dropout值条件下平均分类结果，然后结合式(2)和式(3)选择样本。

3.2 冗余度算法

如图1(a)所示，上述不确定性方法选择样本过程仅是按照给定计算指标排序选择一些样本作为Si集，该过程中并没有考虑样本冗余，从而选择了无意义的样本。基于此问题提出DRAL方法，如图1(b)所示，将位于CNN分类边界附近的样本构成候选样本集，该集合包括所有类别。最后，从该候选样本集中选择冗余度小的样本子集。

根据不确定性方法选择位于CNN分类边界附近的样本构成候选样本集。计算所有候选样本间的潜变量间余弦距离矩阵：

(5)

利用距离矩阵得到冗余度小的样本集，即每次从候选集选出与待标记集最不相似的样本，特别地，若L为空集则选择与候选集最相似样本。冗余度算法如算法1所示。

算法1冗余度算法

输入：距离矩阵D；样本数目k。

输出：待标记样本集L。

1. While |L|

2. IfL=∅:

3.P=average_column(D);/*根据式(5)计算距离矩阵D行均值向量*/

4. Index=min(P);/*得到与整个候选集最相似的样本索引*/

5. Else

6.D1=D(L);P=average_row(D1);/*按照L中样本在候选集中索引，把D行向量拼接成D矩阵，计算D列均值*/

7. Index=max(P);/*取出与L样本集最不相似的样本*/

8.L=L+index;/*做标记，放入L中*/

9.D=L-D；/*按照L中样本在候选集中索引，把D列向量删除*/

10. End while

11. returnL

3.3 DRAL方法

从上述算法可看出，利用余弦距离、冗余度算法的目的是从候选样本集中选择具有类别多样性、冗余度小的样本集。结合上述不确定性方法，DRAL算法过程如算法2所示。

算法2DRAL算法

输入：有标签样本集L；无标记样本集U；每次选择样本数K；候选样本数NK；最大迭代次数T；当前迭代次数t。

输出：CNN模型。

1. 在L上初始化CNN；

2. whilet

3.C=uncertain(U);

/*根据不确定方法(1)或方法(2)或

/方法(3)，在U中选择NK个样本，构成候选集C*/

4.Dis=D(C);

/*计算所有样本之间余弦距离，构成距离矩阵D*/

5.Q=R(Dis,K);

/*由算法1可得，从候选集C中得到样本

/数目为K的待标记样本集Q*/

6.L=L+Q;U=U-Q;

/*在有标签集添加Q，从无标签集删除Q*/

7. CNN=train(CNN,L);

/*在L上训练CNN*/

8. end while

9. return CNN

假设在无标记样本池中，一轮内选出K个样本，以LeNet-5网络为分类器有S个卷积核，设单个卷积核计算时间为ts，DRAL方法和不确定性方法的时间复杂度分析如下：

不确定性方法：

TU=Ts+Tk

(6)

DRAL方法：

TD=Ts+Tk+TR

(7)

式中：Ts是经过网络训练时间;Tk是排序选择样本时间;TR是冗余度计算时间。

Ts=tsKS=O(tsS)

(8)

Tk=K=O(1)TR=NK=O(N)

(9)

显然，tsS≫N>1，则Ts≫TR>Tk，时间主要消耗在训练神经网络上，则式(6)与式(7)有如下关系：

TU≈TD≈O(tsS)

(10)

由式(10)可得出两种方法的运行时间大致相同。

4 实验与结果分析

4.1 数据集和网络结构

在Lenet和NIN模型上对Mnist、Fashion-mnist,以及Cifar-10进行多次实验。神经网络结构见表1和表2，数据集的说明如下：

(1) Mnist：28×28灰度图，共10类。用于识别手写数字数据集，其中:训练集50 000幅，验证集5 000幅，测试集10 000幅。实验用10 000幅作为无标记样本池。

(2) Fashion-mnist：28×28灰度图，共10类。用于识别时尚服装数据集，其中:训练集50 000幅，测试集10 000幅。由于复杂度比Mnist更高，实验用20 000幅作为无标记样本池。

(3) Cifar-10：32×32×3彩色图，共10类。用于识别普适物体的小型数据集，其中:训练集50 000幅，测试集10 000幅。实验用20 000幅作为无标记样本池。

表1 Mnist和Fashion-mnist实验网络结构

表2 Cifar-10实验网络结构

续表2

4.2 实验参数

为了降低实验偶然性的影响，每个数据集实验都是平均了5次的结果。每次实验中，为了避免模型在训练过程中具有倾向性，每次迭代选择的验证集是从现有的有标签集中的每类随机均匀抽取2%样本，且在各个数据集实验的CNN初始化网络参数一样。

实验使用Python平台的Keras工具包，将DRAL方法与不确定性方法中的低可信度[26]、信息熵[26]和贝叶斯方法[8]进行了多次对比。对于Mnist数据集，n0=100,T=15,N=3,K=100,特征向量长度128，网络结构见表1。对于Fashion-mnist数据集，n0=200,T=20,N=10,K=150，特征向量长度256，网络结构见表1，特别地，Fc层输出长度变为256。Cifar-10数据集，考虑到数据集复杂性和网络训练问题为了能减少过拟合和结果稳定性，dropout值降低，n0=1 000,T=20,N=30,K=150，dropout=0.25，特征向量长度512。本文实验对比的是3.1节的不确定性方法。

4.3 实验结果分析

为了验证DRAL算法有效性，由于数据集的复杂度不同，因此不同的数据集使用不同的网络结构。结果见图2。

图2 DRAL算法在不同数据集上的实验结果

可以明显看出，DRAL算法在原有的不确定性方法中有明显的提升。以不确定性方法的最高准确率所需样本为对比，在Mnist中，不确定性方法达到98%时，entropy最高减少28%样本，Bayesian方法最低减少16%样本；在Fashion-mnist中，不确定性方法达到85%时，least最高减少30%样本，entropy最少减少14%样本；在Cifar-10中，三种方法在达到52%准确率时，least最高减少22%，Bayesian最少减少11%样本。从上述结果分析可知，DRAL方法在三种方法最高减少30%样本，最低减少11%样本。

从这些结果中可以发现，原来的三种不确定性方法所选择的样本的信息对于分类器而言具有冗余性。因为DRAL算法主要是经过冗余度算法选出冗余度小的样本集。图2中准确率升高，相同样本数目下，信息量变大，冗余度因此降低。以时间为代价，DRAL方法可以合理有效提升不确定性方法。

为了降低潜变量特征向量长度和候选样本数目对样本冗余度研究的影响，对潜变量特征向量长度和候选样本数目进行了实验。在Fashion-mnist中，特征向量分别是128和256以及候选样本数目分别是300和1 000的条件下，都经过DRAL-least方法的两组实验。信息冗余度与特征向量长度和候选样本数目关系实验结果如图3所示。

图3 DRAL算法中特征向量长度和候选样本数与冗余度的关系

图3(a)实验是在Fashion-mnist数据集中，候选样本数量1 000的条件下，特征向量长度分别为128和256。由于CNN在最后一层的宽度不同，所以初始化网络参数不一致，对于此问题，本实验尽可能让初始化网络在测试集上效果相同。可以看出，当模型准确率达到80%时，前者比后者多了100个有标记样本。所以，特征向量越长所带有的信息量更多。

图3(b)实验是在同样的数据集中，在n0=200、T=20、K=100、特征向量长度为256的条件下，候选集的样本数量分别是300和1 000，初始化网络参数均相同。同样地，当模型准确率达到80%时，前者比后者多用了100个有标记样本。通过该实验可以比较出，若候选样本数量较少时，候选样本集所带有的信息量不足，但冗余度小，此时会受到样本数目的影响。

经过上述实验可以看出，经过CNN计算得出的特征向量维度越高，候选样本越多带有的信息量越多，经过DRAL算法提升后效果越明显。而所选择的候选样本数目越多，信息冗余性越强。经过DRAL算法提升效果越好。

5 结 语

在主动学习池样本选择模式下，本文提出一种减少样本信息冗余的DRAL方法，使用不确定性方法经过CNN选择大量的候选样本构成候选集，在候选集中利用样本余弦距离关系进行第二次筛选，从而得到信息量较大且冗余度小的样本集。该方法可以有效地减少样本数据冗余，进一步减少模型所需的有标记样本数量。未来可以进一步优化不确定性方法。