基于粒化单调的不完备混合型数据增量式属性约简算法
张雨新 孙达明 李 飞
1(唐山工业职业技术学院信息工程系 河北 唐山 063299)
2(东北大学计算中心 河北 秦皇岛 066004)
0 引 言
属性约简[1-2]又称为特征选择,目前在机器学习和数据挖掘等领域发挥了很重要的作用[3]。然而在实际工程应用中,数据集往往是不断动态增加的,而传统的属性约简算法进行运用时会产生大量的重复计算和时间开销,不利于实际的应用。为了改善这一局限性,学者们将增量式学习应用在传统的属性约简中,提出了增量式的属性约简方法[4-5],从而满足了动态数据集属性约简的时效性。
不完备信息系统[6]是一种常见的信息系统类型,即数据集中的某些属性值是缺失的。对于这类数据集,学者们不断地进行了增量式的属性约简研究。Meng等[7]基于不完备信息系统的正区域提出了一种快速的属性约简算法,用来提高对于动态数据的属性约简效率。Shu等[8]针对不完备信息系统属性变化的情形,提出了正区域的增量式更新,进而构造出了相应的增量式属性约简算法。针对这类问题,李成等[9]也提出了类似的算法,同时Shu等[10]针对不完备信息系统对象增加的情形,设计了一种新的增量式属性约简算法。进一步地,Shu等[11]提出了一种改进的增量式属性约简算法,优化了原先算法的效率。根据一致性度量,Xie等[12]在对象增加、属性增加、属性值变化方面,提出了一种新的增量式属性约简算法。针对区分矩阵的方法,丁棉卫等[13]提出了一种二进制区分矩阵的不完备系统增量式属性约简算法。在其他类型的不完备信息系统中,Luo等[14]提出了一种不完备多尺度信息系统的增量式算法。
然而,实际数据环境下的很多不完备信息系统既包含了离散型的属性也包含了连续型的属性,称这类信息系统为不完备混合型信息系统[15],目前对这类信息系统的增量式属性约简研究甚少。本文针对这一问题,提出一种属性增加时的增量式属性约简算法。
对于不完备混合型信息系统,Zhao等[15]将邻域关系和容差关系进行结合,提出了邻域容差关系,并根据该二元关系,在不完备混合型信息系统下提出了邻域容差条件熵,相应的属性约简算法也被提出。本文在Zhao等的基础上,证明邻域容差关系随属性增加时的粒化单调性;然后基于这种粒化单调性,研究邻域容差条件熵的增量式更新,并利用该更新机制设计出相应的增量式属性约简算法;最后通过实验来验证算法的有效性。
1 基本理论
1.1 粗糙集模型与不完备混合型信息系统
在粗糙集理论[3]的研究范畴内,数据集被格式化成信息系统的形式。通常一个信息系统可简单表示为一个三元组IS=(U,AT,V),其中:U称为信息系统的论域,是数据集所有对象的集合;AT称为信息系统的属性集;V表示信息系统所有属性值的集合,即对于∀x∈U且∀a∈AT,a(x)∈V,这里a(x)表示对象x在属性a下的属性值。在实际中,信息系统的属性值可能是缺失的,并且连续型的属性值和离散型的属性值并存,对于这类信息系统,称之为不完备混合型信息系统[15]。
对于不完备混合型信息系统,Zhao等[15]联合邻域关系和容差关系提出了一种邻域容差粗糙集模型,该模型通过构造邻域容差关系来对论域进行知识粒化,作为该模型的理论计算基础。
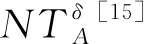
(a(y)=*)∪((a∈AD→a(x)=a(y))∩
(a∈AN→|a(x)-a(y)|≤δ))}
(1)
式中:δ为邻域半径,是一个非负常数;“*”表示缺失的属性值。


式中:U={x1,x2,…,xn}。
1.2 不完备混合型信息系统的条件熵与属性约简
属性约简是粗糙集理论的研究重点[3],属性约简的目的是对原信息系统中选择一个极小的属性子集,使得这个属性子集与原属性集具有相同的分类能力[16-17]。在不完备混合型信息系统中,Zhao等[15]基于条件熵的方式提出了一种属性约简方法。
定义1[15]对于不完备混合型信息系统IS=(U,AT,V),U={x1,x2,…,xn},邻域半径为δ。属性子集A1,A2⊆AT诱导的邻域容差粒化分别表示为:
那么A2关于A1的条件熵定义为:
(2)

(3)
式中:[xi]D表示对象xi在决策属性集D下的等价类。
定义2[15]对于不完备混合型决策信息系统IS=(U,C∪D,V),若red⊆C是该信息系统的条件熵属性约简,则同时满足:
(1)E(D|C)=E(D|red)。
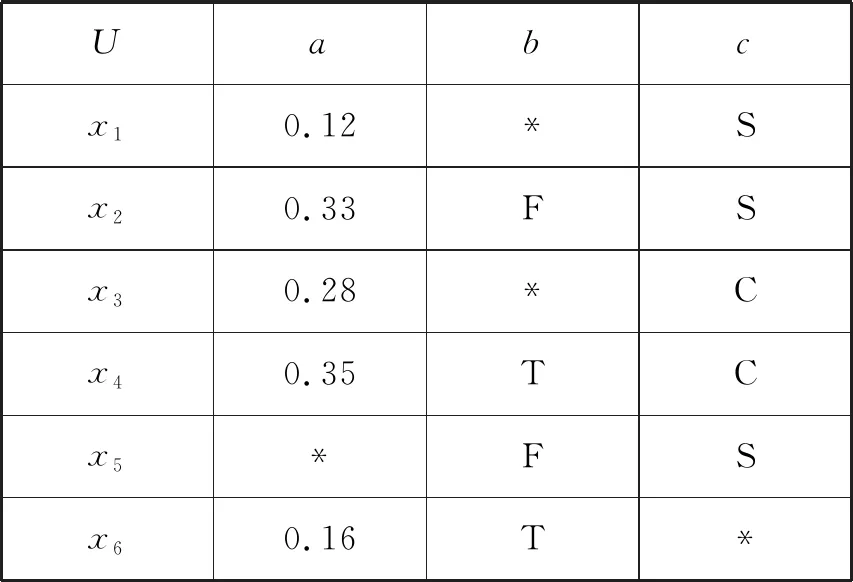
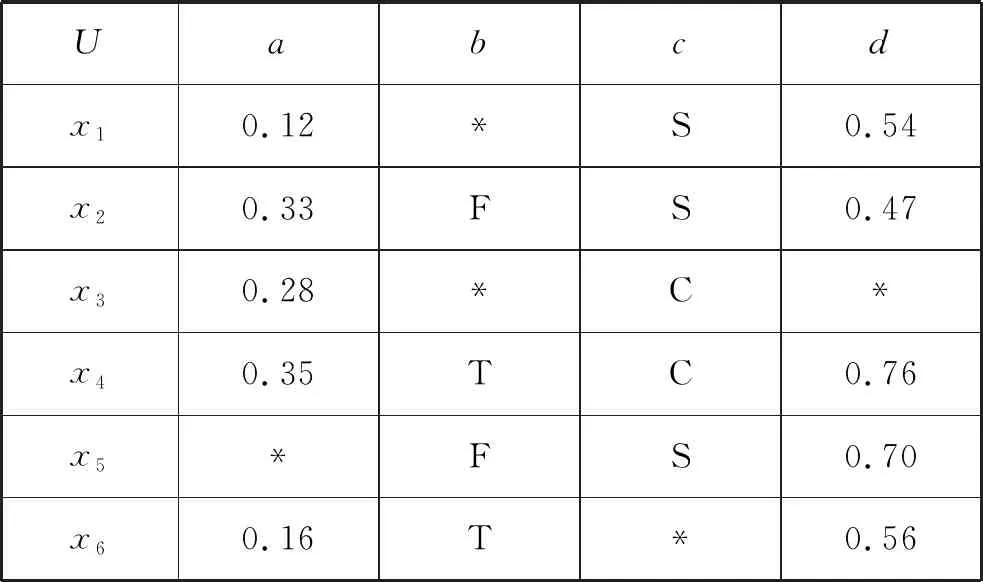
(2) ∀a∈red,E(D|red) 基于定义2所示的属性约简定义,其对应的属性约简算法如算法1所示。 算法1[15]不完备混合型信息系统的条件熵属性约简算法 输入:不完备混合型决策信息系统IS=(U,C∪D,V),邻域半径δ。 输出:属性约简结果red。 步骤1初始化red←∅。 步骤2令E(D|φ)=1。遍历C-red中每个属性a,计算属性a的条件熵属性重要度: sig(a)=E(D|red)-E(D|red∪{a}) 步骤3对于步骤2中C-red所有属性,找出属性重要度最大的属性,记为amax。 步骤4若sig(amax)=0,则转步骤5;若sig(amax)>0,则red←red∪{amax},并返回步骤2。 步骤5返回属性约简结果red。 在算法1中,通过条件熵作为启发式函数进行属性的选择,直至达到条件E(D|C)=E(D|red)成立时算法终止,选择出的red为最终的属性约简结果。算法1的时间复杂度为O(|C|2·|U|2)[15]。 在实际应用领域,信息系统时刻处于动态更新之中,此时传统的属性约简算法不再有效[4],对传统的算法构造增量式学习,设计出增量式的属性约简是目前的主要研究方向[8-14]。属性集的动态增加是信息系统动态更新的一种常见情形,对于条件熵的属性约简算法,当不完备混合型信息系统有新的属性集加入时,计算新的约简时需要重新进行条件熵的计算,这无疑会增加时间开销。本节针对不完备混合型信息系统中属性集增加的情形,提出条件熵的增量更新方法。 对于完备型的信息系统,当属性增加时,由于论域的粒化满足单调性,因此学者们通过等价类的变化进行相关启发式函数的增量式计算[8-9,12]。本节同样采用这一思路,通过邻域容差类的粒化单调性去更新条件熵,提出一种高效的条件熵增量式更新方法。 证明:由于P⊆Q,根据邻域容差关系的定义有: 证毕。 性质1表明,对于不完备混合型信息系统的邻域容差关系,当属性集增加时,其中每个对象的邻域容差类是逐渐减小的,即邻域容差类满足粒化单调性。 例1表1所示的是一个不完备混合型信息系统,其中:论域U={x1,x2,x3,x4,x5,x6};属性集AT={a,b,c};属性a为连续型属性;属性b和属性c为离散型属性;“*”表示缺失的属性值;F、T、S、C代表了对应的属性值,无实际含义。 表1 不完备信息系统 令P={a,b},Q={a,b,c},邻域半径δ=0.1。根据邻域容差类的定义,有: 令: (4) 定义3表明,在不完备混合型信息系统中,当属性集发生增加时,一部分邻域容差类会减小,一部分邻域容差类可能保持不变。根据如上所述的变化规律,接下来可以推导出条件熵的增量式更新。 E(A2|A′1)=E(A2|A1)-Δ (5) 证明:根据定义1有: 根据性质1有: 根据集合的计算法则,可以得到: 又由于: 所以: 对于∀x∈U,记: 那么 因此: 显然∀x∈U有Ψ(x)⊆Φ(x),即: |Φ(x)|-|Ψ(x)|=|Φ(x)-Ψ(x)|= 因此E(A2|A′1)=E(A2|A1)-Δ,其中: 根据定义3,其中: 即: 因此: 那么: 证毕。 E(D|A′)=E(D|A)-Δ 例2在例1的基础上,假设不完备混合型信息系统增加属性集ΔA={d},新的信息系统如表2所示,此时AT′={a,b,c,d}。 表2 新的不完备信息系统 根据定义1有: 根据定理1有: 如果采用定义1的方法,得到的计算结果是一致的。 本节根据条件熵增量式更新,提出不完备混合型信息系统属性增加时的条件熵增量式属性约简算法。 对于不完备混合型信息系统IS=(U,C∪D,V),约简集为red。当新的属性集ΔC加入条件属性集时,新的信息系统表示为IS′=(U,C′∪D,V′),其中C′=C∪ΔC。算法2所示为基于属性增加时的条件熵增量式属性约简算法。 算法2属性增加时不完备混合型信息系统的条件熵增量式属性约简算法 输入:增加属性集ΔC后新的不完备混合型决策信息系统IS′=(U,C′∪D,V′);邻域半径δ;旧信息系统IS的属性约简red;条件熵E(D|red)。 输出:新的属性约简结果red′。 步骤1初始化red′←red。 步骤2根据条件熵E(D|red)按照定理1增量式计算新的条件熵E(D|C′),判断E(D|C′)与E(D|red)之间的大小关系:若E(D|C′)=E(D|red),那么跳转入步骤5;若E(D|C′) 步骤3遍历C′-red′中每个属性a,计算属性a的条件熵属性重要度: sig(a)=E(D|red′)-E(D|red′∪{a}) 找出C′-red′中属性重要度sig(a)最大的属性,记为amax。 步骤4若sig(amax)=0,那么跳转入步骤5,若sig(amax)>0,则red←red∪{amax},并返回步骤3。 步骤5对于属性集red′中的每个属性a,若存在E(D|red′-{a})=E(D|red′),那么red′←red′-{a}。重复进行步骤5,直到不存在这样的属性。 步骤6返回属性约简结果red′。 表3所示为实验中所使用的数据集,其中所有的数据集均来源于UCI 标准数据集库,在这6个数据集中,Cylinder、Sick和Annealing为连续型和离散型属性混合的不完备数据集。整个实验环节采用Windows 7操作系统、Inter (R) Core (TM) i7-2700 CPU (3.5 GHz)和8.00 GB内存的个人电脑,算法采用MATLAB 2015b进行编程实现和运行。 表3 实验数据集 本实验的流程如下,首先分别使用算法1和算法2对表3中的6个数据集分别进行动态的属性约简,通过比较属性约简所需的时间开销来证明所提出算法的增量式属性约简效率。在属性约简的过程中,通过比较每次数据集属性约简结果的分类精度,来验证所提算法属性约简的优越性。 表3所示的是静态的不完备数据集,为了模拟数据集属性动态变化的情形,本实验采用原始数据集属性递增的方式进行处理,即原始数据集按照属性平均分成7个属性子集,从属性空集开始每次增加一个属性子集来生成数据集属性的一次动态更新,这样便可以实现数据集属性的7次更新。整个实验均采用这种方式进行实验。 在算法1和算法2中,邻域半径δ是算法的入参,它的取值不同对最终的属性约简结果将产生很重要的影响,本节将通过实验的方法对邻域半径δ选取合适的参数。对邻域半径在[0,0.3]中以0.02为间隔分别进行取值,然后将对应的邻域半径分别作为算法2的入参进行增量式属性约简,每次增量式属性约简将会得到对应的属性约简集,利用SVM分类器对约简集进行分类精度计算,从而得到该约简集下的分类精度,所有数据集的实验结果如图1所示。 (a) Cylinder (b) Sick 观察图1可以发现,随着数据集属性增量次数的增加,属性约简结果的分类精度是逐渐增大的,对于不同的邻域半径δ,当取值在0.12~0.16之间时得到的分类精度大致是最高的,本实验将邻域半径设定为δ=0.14进行实验。其中数据集Mushroom的分类精度不随邻域半径的变化而变化,这主要是由于该数据集为不包含连续型属性的数据集,因此实验结果不受邻域半径影响。 图2所示为算法1和算法2在6个数据集下动态属性约简的用时比较结果。 (a) Cylinder (b) Sick 数据集刚开始进行增量式更新时,算法1和算法2的属性约简用时相近,当数据集更新次数逐渐增多时,两种算法的约简用时出现明显的差距,其中算法1的增加速率逐渐增大,而本文所提出的算法2,随着属性更新次数的增加,其约简用时增长较为缓慢。出现这种现象的主要原因是由于算法2是一种增量式的属性约简算法,数据集每次更新后,算法会在之前属性约简结果的基础上进行计算,避免了对旧数据集的重复计算;同时对于属性的逐渐增加,信息系统论域的粒化愈加精细,导致信息系统再增加属性集时,对象的容差类很难发生很大的变化。因此算法2具有较高的动态属性约简效率。 属性约简旨在找到与原始属性集具有相同区分能力的属性子集,而具有相同区分能力的属性子集可能具有不同的分类性能,因此具有更高分类性能的属性子集则更加优越。本节比较两类算法属性约简结果的分类性能,其中属性集的分类性能通过支持向量机分类器(SVM)进行评估,即通过属性子集十折交叉验证的分类精度去衡量。 在数据集属性每次动态更新中,算法1和算法2都会得到当时数据集的属性约简结果,然后利用SVM分类器对约简结果进行分类训练,便得到了对应的分类精度,其结果如表4所示。可以发现本文所提出的算法2在大部分情形下具有较高的分类性能,例如:在数据集Sick中,算法2在第6次的更新结果中分类精度达到了86.42%,而算法1只有83.08%;在数据集Iono中,算法2第5次实验结果的分类精度为99.92%;在数据集Mushroom中,算法2第6次实验结果的分类精度为95.37%。在某些情形下,算法1的分类精度稍高于算法2,例如数据集Cylinder的第3次结果,数据集Annealing的第2次结果等。结果表明算法2的约简结果具有较高的分类性能。 表4 增量式属性约简分类精度比较 % 综合整个实验部分的所有实验结果,可以看出本文提出的条件熵增量式属性约简算法比传统的算法具有更高的增量式属性约简性能。同时所提出的增量式属性约简算法对于属性增加的动态数据集,具有很高的属性约简效率,因此可以证明所提出的增量式算法的有效性。 本文通过邻域容差关系随属性增加时的粒化单调性,研究了邻域容差条件熵的增量式更新,并且根据这种更新机制提出一种不完备混合型信息系统属性增加时的增量式属性约简算法。实验证明了所提出算法的有效性。接下来将进一步探索不完备混合型信息系统对象增加时的增量式属性约简问题。2 属性变化时条件熵的增量式学习


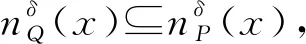
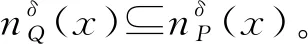

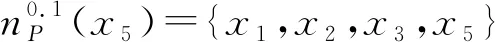
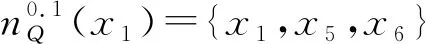
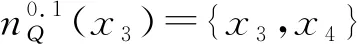
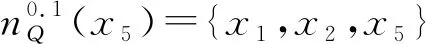


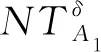


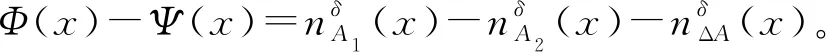

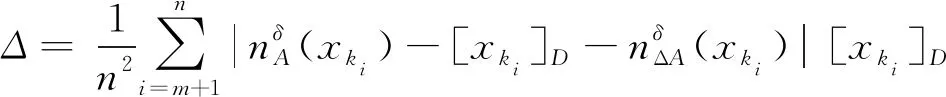
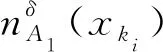
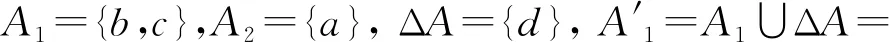
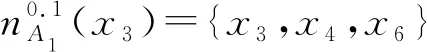
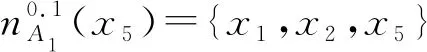
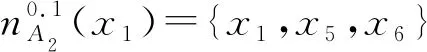
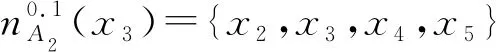
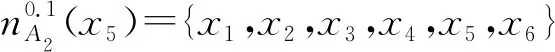

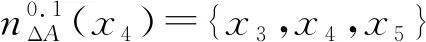

3 增量式属性约简算法

4 实验分析
4.1 实验设计与流程
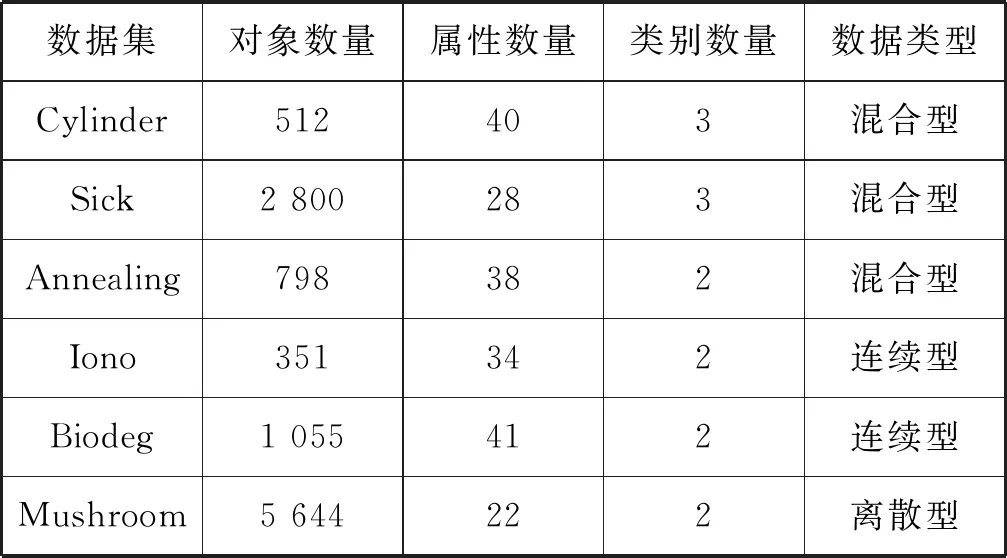
4.2 参数设置
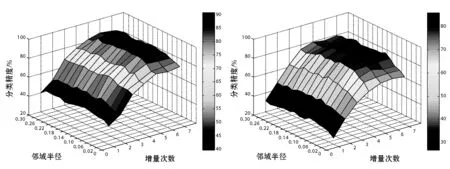
4.3 属性约简效率的比较
4.4 属性约简结果的分类性能比较
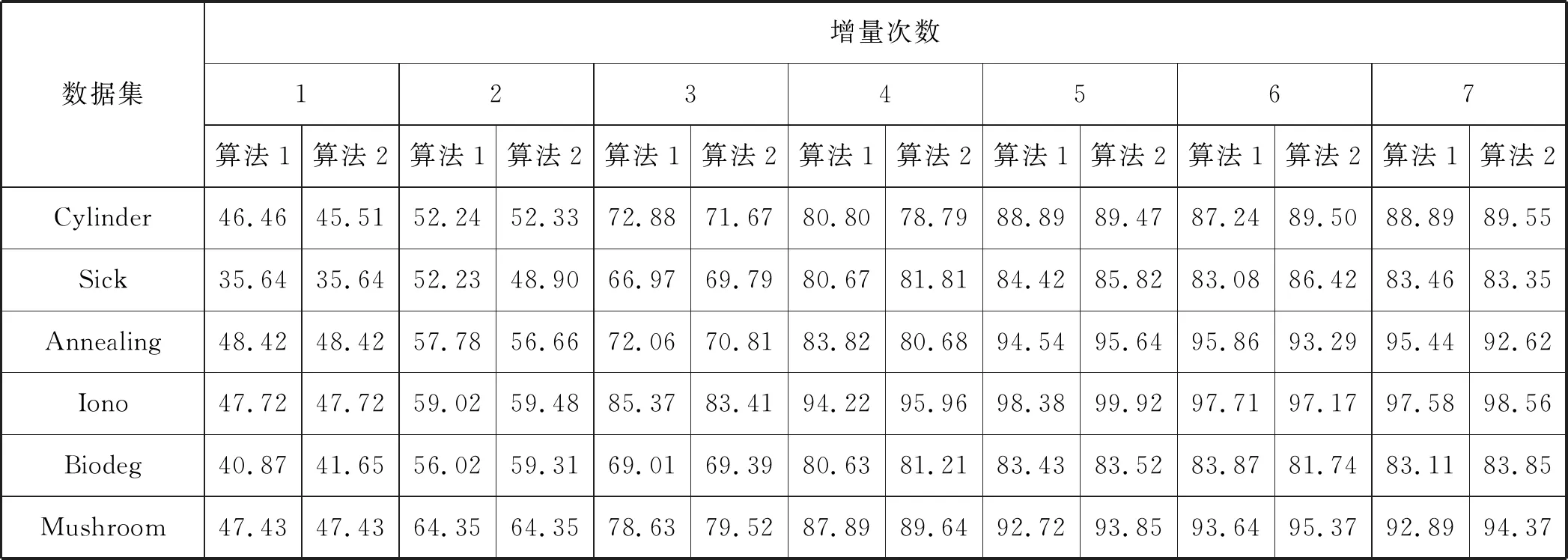
4.5 实验总结
5 结 语

