球状物体作微形变时弹性势能的研究

于凤军, 汤振杰，田俊龙，张希威

(安阳师范学院 物理与电气工程学院，河南 安阳 455000)

1 一般情况下的弹性势能密度

一般情况下, 应变和应力都用张量[2]描述, 在直角坐标系Oxyz中, 设应变张量的各分量为exx,exy,exz,eyx=exy,eyy,eyz,ezx=exz,ezy=eyz,ezz; 应力张量的各分量为:σxx,σxy,σxz,σyx=σxy,σyy,σyz,σzx=σxz,σzy=σyz,σzz. 由文献[2]式(12.5-3)可知, 当应变张量的各分量改变δeij(i,j=x,y,z)时，应变能密度w的增量为

δw=σxxδexx+σyyδeyy+σzzδezz+

2σxyδexy+2σyzδeyz+2σzxδezx

(1)

文献[2]式(12.6-7)给出各向同性的均匀弹性体的胡克定律：

(2)

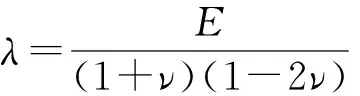
(3)

由于本文所研究的系统不可压缩, 即无体积膨胀, 故上式中的相对体膨胀为

θ′=exx+eyy+ezz=0

(4)

对于球体, 取球坐标系(r,θ,φ)更方便, 应变张量的分量为err,erθ,erφ,eθr=erθ,eθθ,eθφ,eφr=erφ,eφθ=eθφ,eφφ.考虑式(4), 将式(3)变换到球坐标系, 得弹性势能密度

(5)

当应变张量eij(i,j=r,θ,φ)已知时，通过上式在球内进行积分，就可得到弹性势能.

2 弹性球的形变描述

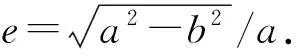
图1 弹性球形变为长旋转椭球

(x2+y2)/b2+z2/a2=1

(6)

将x=rsinθcosφ,y=rsinθsinφ,z=rcosθ代入上式得

(7)

由于e<<1，将上式展开, 仅保e的最低次项

(8)

上式是椭球表面在球坐标系中的方程, 其中P2(cosθ)是勒让德函数.

当弹性球表面形变为椭球表面时, 其体内每一点将离开原来的位置产生微小位移. 设点(r,θ,φ)处质点的位移为

S(r,θ,φ)=Srer+Sθeθ+Sφeφ

(9)

其中,er,eθ,eφ分别是径向、经线切向、纬线切向的单位向量,Sr、Sθ、Sφ分别是位移沿er,eθ,eφ方向的分量，它们都是点的坐标(r,θ,φ)的函数. 根据文献[3]式(13.5.14)知, 应变张量分量与位移分量的关系为

(10)

式(8)、式(9)、式(10)构成对弹性球形变的描述. 如果知道位移分量Sr、Sθ、Sφ的具体函数式, 则通过式(10)可以确定应变张量，再由式(5)和体积分计算, 求弹性势能.

3 位移分量Sr、Sθ、Sφ函数式的确定

由于弹性球沿z方向拉长为长旋转椭球, z方向处于er、eθ构成的平面内, 故体内各质点的位移可能有er、eθ方向的分量, 不可能有eφ方向的分量, 即Sφ=0. 因为椭球具有绕z轴的旋转对称性, 所以Sr、Sθ与φ无关, 仅是r、θ的函数,故设Sr=u(r)f(θ),Sθ=v(r)g(θ),其中u(r)、f(θ)、v(r)、g(θ)是待定函数. 综上所述, 位移分量可表示为

(11)

本问题的边界条件是: 球面上各质点的径向位移使球面变成由式(8)决定的椭球面, 各点的切应力和切应变为0, 即erθ|r=R=0. 此外, 还受到不可压缩条件(4)的约束, 并且位移为有限值. 下边利用这些条件求待定函数.

根据式(8), 球面上质点的径向位移条件、即边界条件为

(12)

令式(11)第一式中r=R, 并与式(12)对比，得

(13)

f(θ)=P2(cosθ)

(14)

故Sr=u(r)P2(cosθ). 将此表达式和Sθ=v(r)g(θ)代入式(10)第四式运算，将得到erθ的表达式(注:下边所有复杂的公式推导皆由Mathematica软件完成)，然后再利用边界条件erθ|r=R=0，得

(15)

由上式可得,g(θ)=Kcosθsinθ, 其中

(16)

为常数. 将式(14)、上述g(θ)代入式(11)得

(17)

在球坐标系中, 不可压缩条件(4)可变换作:

err+eθθ+eφφ=0

(18)

把式(17)分别代入式(10)的前三式后, 一并代入式(18)化简, 有如下结果:

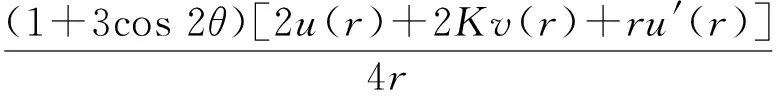
(19)

由于上式中因子(1+3cos 2θ)不恒等于0, 故有2u(r)+2Kv(r)+ru′(r)=0, 即

(20)

根据上式和式(17), 位移分量表示为

(21)

至此, 位移分量函数式(21)中仅剩一个待定函数u(r).u(r)的一个边值条件为式(13), 另一边值条件可由式(20)先确定出v(R)、v′(R)，再代入式(16)得到

R2u″(R)+2Ru′(R)+4u(R)=0

(22)

下面由最小势能原理确定u(r)满足的微分方程. 将式(21)代入式(10), 式(10)再代入式(5), 并在整个球内积分, 可得弹性势能:

26r2u′2+32ruu′+32u2]dr

(23)

显然,W的大小与u的函数形式有关. 根据最小势能原理, 当一个力学系统平衡时, 势能取最小值. 因此，现在的问题是上式中当u取何种函数形式时能使W最小,W的最小值是什么. 这是一个泛函的极值问题[4]. 令

26r2u′2+32ruu′+32u2

(24)

将上式代入欧拉方程[4]:

(25)

可得u(r)满足的方程:

r4u″″2+8r3u′″-24ru′+24u=0

(26)

上式是欧拉型常微分方程, 对其有现成的解法[5], 其特征方程为

γ(γ-1)(γ-2)(γ-3)+8γ(γ-1)(γ-2)-

24γ+24=0

(27)

这是一个一元4次方程, 容易验证，γ的4个根为: -4,-2,+1,+3. 故u(r)的通解为

u(r)=Ar-4+Br-2+Cr+1+Dr+3

(28)

其中,A、B、C、D是待定常数. 当r=0时u(r)有限, 所以A=B=0. 据此, 将式(28)分别代入边值条件(13)、(22)，得二元一次方程组:

(29)

解得:C=8e2/15,D=-e2/(5R3). 故由式(28)得

(30)

把上式代入式(21), 可得位移分量函数式的最终结果

(31)

4 弹性势能的计算结果

将式(30)代入式(23)运算, 可得弹性势能

(32)

其中,V=4πR3/3为球体积.

5 讨论

1) 与直杆的弹性势能对比. 式(32)表明, 当弹性球形变为长旋转椭球时, 其弹性势能与变形参数——椭球偏心率e的4次方成正比, 与弹性模量和体积成正比. 我们将这一结果与直杆的弹性势能作个对比. 令式(8)中θ=0, 可得弹性球在z方向的半径相对变化:(r-R)/R=e2/3, 这也是直径沿z方向的相对变化Δd/d=e2/3, 即e2=3Δd/d. 另外, 切变模量与杨氏模量关系为μ=G=E/(1+ν)/2. 将上二式代入式(32)

(33)

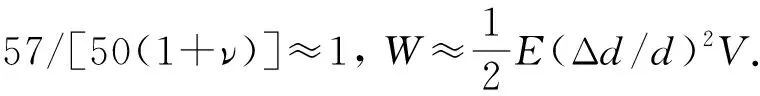
2) 弹性势能分布.将式(31)代入式(10), 式(10)再代入式(5), 可得势能密度与点坐标(r,θ,φ)的关系:

24r2(7r2-8R)cos 2θ+9r4cos 4θ]

(34)

根据上式能够了解势能密度沿径向的变化情况. 如图2，设原点的势能密度为wo，以比值r/R为横轴，以比值w/wo为纵轴， 分别作出θ沿0°、45°、90° 3个方向上w/wo随r/R的变化曲线. 图中3条曲线自下而上分别对应0°、45°、90°. 显然, 椭球中心的势能密度最大.大体上讲, 距中心越远, 势能密度越小.这一特点也可以通过“等势能密度线”图看出. 图3给出了通过z轴的任一剖面内的“等势能密度线”图,图中亮度与w成正比. 可以看出, 中心的亮度最高,w最大；偏离中心越远, 亮度越低，w越小.等密度线近似是椭圆, 其长轴垂直于z轴, 这意味着“等势能密度面”近似为绕z轴的扁旋转椭球面.

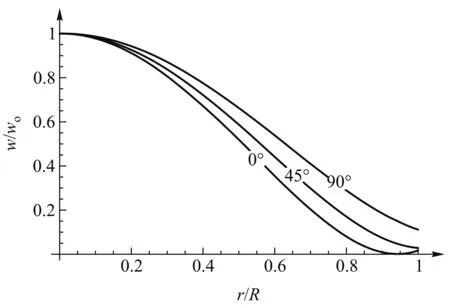
图2 势能密度随径向的相对变化

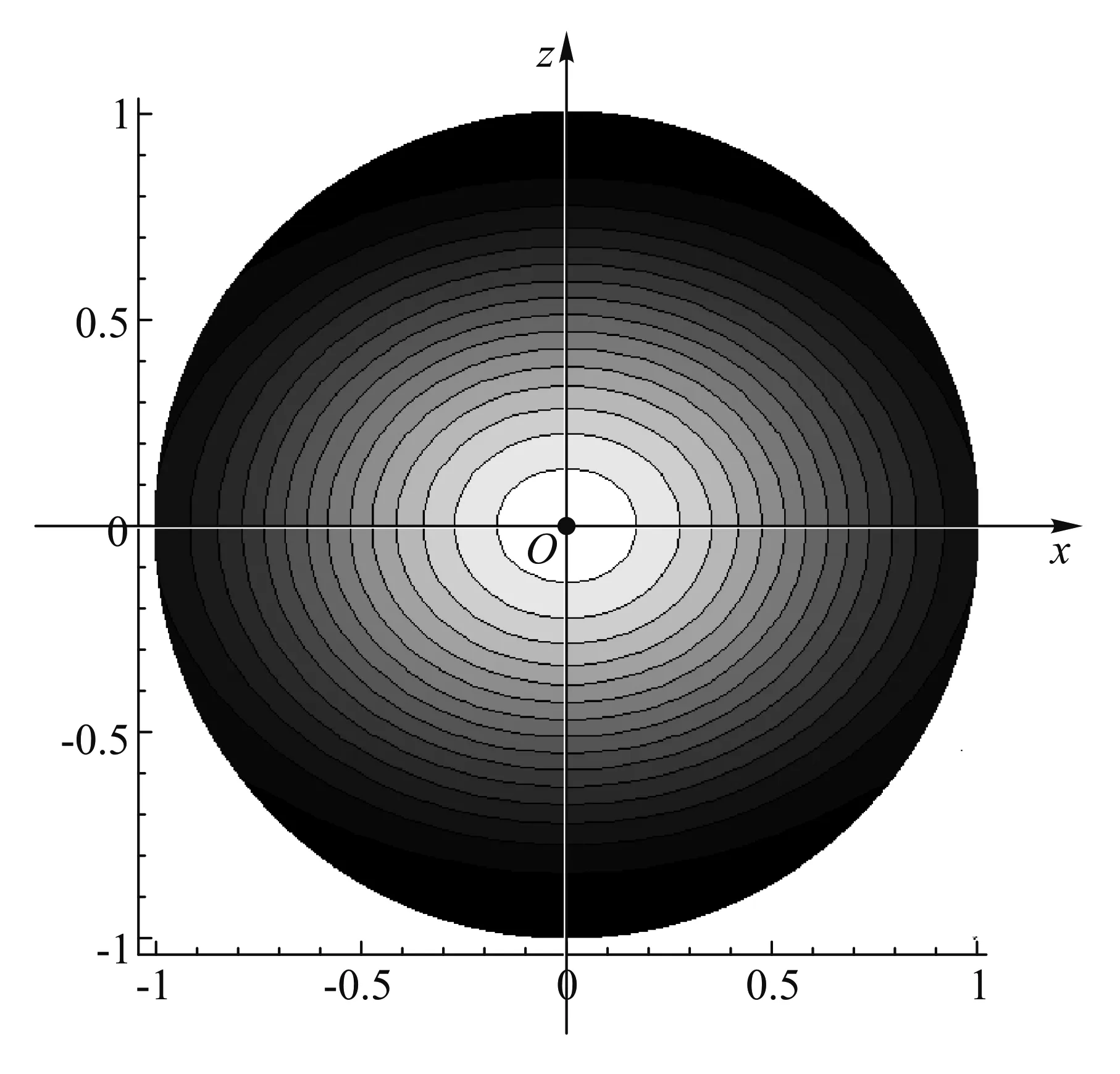
图3 等势能密度线

结语：以上求出一个弹性球形变为长旋转椭球时的弹性势能或应变能. 首先, 通过应变能密度增量公式和胡克定律，导出应变能密度与应变张量的关系式(3)，利用标准椭球方程导出弹性球在保持体积不变的前提下形变的几何描述式(8)；然后，通过一个原理、六个条件确定出位移函数式(31), 它们分别是最小势能原理、椭球沿z方向拉长条件、绕z轴的旋转对称条件、球面上各质点的径向位移条件、球面上各点的切应力切应变为0条件、不可压缩条件、位移有限条件. 最后通过弹性势能密度与应变张量的关系、应变张量与位移分量的关系和体积分，得到本文想要的结果，并且进行了有益的讨论. 本文以阐述物理定律、物理原理和物理条件的如何应用为主线，对于数学部分，由于运算工作量很大，对求偏微分、多重积分、化简等，都使用Mathematica软件完成. 因此，本文不仅能作为弹性势能方面的教学案例，也可作为学生学习Mathematica软件的实践素材.