求解变分不等式问题和不动点问题公共点的惯性次梯度外梯度算法

黄 瑕， 夏福全， 张双德

（四川师范大学 数学科学学院，四川成都610066）

0 引言

设H是Hilbert空间，〈·，·〉和‖·‖分别表示H中的内积和范数，C⊂H是一个非空闭凸集，映射F：H→H.经典的变分不等式问题为：求x*∈C，使得

为简单起见，记变分不等式问题（1）为VI（C，F），VI（C，F）的解集为SOL（C，F）.设映射S：C→C为非扩张映射，即

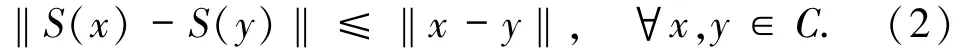
用Fix（S）表示S的不动点集合，即Fix（S）＝｛x∈C：S（x）＝x｝.

本文考虑的问题为：求x*∈C，使得

为了在Hilbert空间中求Fix（S）与SOL（C，F）的公共点，很多学者提出多种迭代算法［1-8］.在2006年，Nadeshkine等［4］提出了一种求Fix（S）与SOL（C，F）的公共点的迭代算法其中，F：H→H为单调Lipschitz连续映射，Lipschitz常数为L＞0，且在

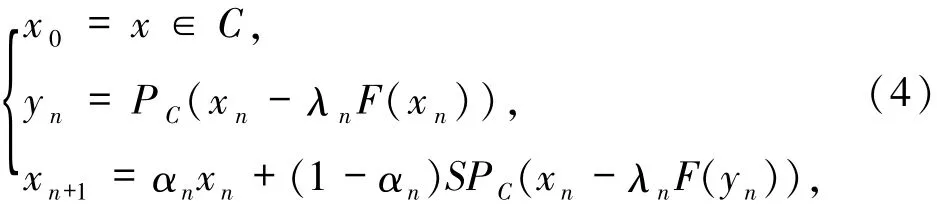
S：C→C为非扩张映射的条件下，证明如果Fix（S）∩SOL（C，F）≠Ø，由该算法生成的序列｛xn｝弱收敛到z∈SOL（C，F）∩Fix（S）.注意到，该算法在每次迭代过程中都会计算2次到C上的投影，如果C是一般的非空闭凸集，投影难以实现.Censor等［7］提出的修正的次梯度外梯度算法6.1，改进了（4）式.他们将（4）式中第二个到C上的投影替换成到一个特定的半空间Tn上的投影，而在Tn上的投影有显示表达式，容易计算.其算法（记为算法1）具体迭代如下：

Censor等［7］在SOL（C，F）非空和F是单调Lipschitz连续映射的条件下证明了该算法生成的序列｛xn｝弱收敛到Fix（S）与SOL（C，F）的公共点.

近年来，惯性型算法的研究备受人们的关注.惯性型算法起源于“带摩擦的重球”动力系统，详见文献［9-10］，其主要特点是利用上一步迭代点以及当前迭代点，通过迭代获得下一步迭代点，目的是加快收敛速度［11-13］.许多学者将惯性算法应用到不同的问题上，比如针对某些可分离的非凸优化问题.Ochs等［14］提出了惯性forward-backward分裂法；针对强凸问题，Ochs等［15］提出了惯性近似算法；针对变分不等式问题，Dong等［16］提出了惯性收缩算法.

受以上文献研究成果的启发，本文将Censor等［7］介绍的修正的次梯度外梯度算法与惯性算法相结合，提出一种解变分不等式问题解集与非扩张映射不动点集的公共点的惯性次梯度外梯度算法，并且在一定的条件下，证明由该算法生成的序列弱收敛到Fix（S）与SOL（C，F）的公共点.

1 预备知识

用xn→x表示序列｛xn｝∞n＝0强收敛到x，用xn⇀x表示序列｛xn｝∞n＝0弱收敛到x.首先给出本文会用到的定义和引理.

定义1.1设C⊂H为非空闭凸集，对∀x∈H，定义

为x在C上的投影.

引理1.1［17］设C⊂H为非空闭凸集，x∈H，则

引理1.2［18］设H为Hilbert空间，则

引理1.3［18］设C⊂H为非空闭凸集，T：C→C是一个非扩张映射，且Fix（T）≠Ø.如果C中序列｛xn｝满足则有z＝T（z）.

定义1.2设映射F：H→H，映射S：C→C，其中C⊂H为非空闭凸集，称F在集合C上是：

1）L-Lipschitz连续的，如果存在常数L＞0，满足

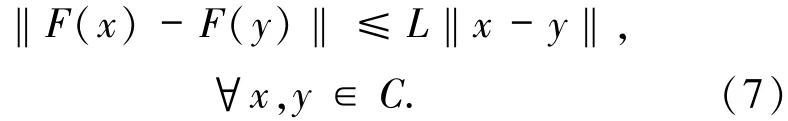
2）单调的，如果

定义1.3令A：H→→2H是实Hilbert空间中的一个集值映射.如果A是单调的，即

〈w-v x-y〉≥0， ∀w∈A（x），v∈A（y），且A的图G（A）：＝｛（x，w）∈H×H：w∈A（x）｝没有包含在任何其他单调算子的图中，则称A是极大单调算子.

很明显，A是极大单调算子当且仅当对任意（x，w）∈H×H，如果〈w-vx-y〉≥0，∀（v，y）∈G（A），则有w∈A（x）.

引理1.4［19］设｛φn｝、｛δn｝和｛αn｝是［0，+∞）中的序列，满足

且对任意n≥1，存在一个实数α满足0≤αn≤α＜1，则以下结论成立：

引理1.5［20］设C⊂H为非空闭凸集，｛xn｝是H中的一个序列，满足以下2个条件：

2）｛xn｝的每个序列弱聚点都在C中.则｛xn｝弱收敛到C中一点.

2 算法及收敛性分析

设序列｛αn｝是非减的，0≤αn≤α＜1，选取σ，δ＞0，满足

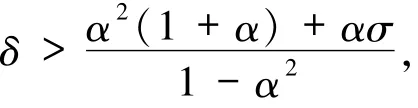
设序列｛βn｝满足

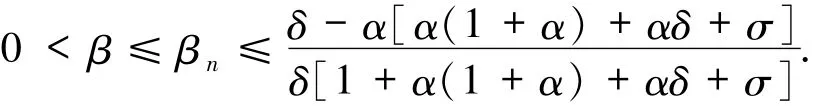
注1显然有βn∈（0，1）.

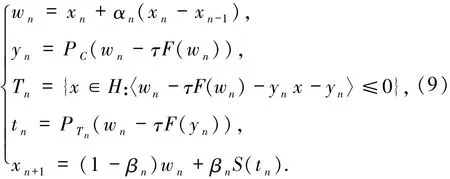
算法2选择初始点x0，x1∈H，τ＞0，

假设以下条件成立.

条件2.1F：H→H是单调映射.

条件2.2F：H→H是Lipschitz连续映射，其Lipschitz常数为L＞0.

条件2.3Fix（S）∩SOL（C，F）≠Ø.

定理2.1假设条件2.1-2.3成立，则当0＜时，由算法2生成的序列｛xn｝弱收敛于SOL（C，F）∩Fix（S）中的一点.

证明 令u∈SOL（C，F）∩Fix（S），由引理1.1以及F的假设条件有

因为F是单调的，可得

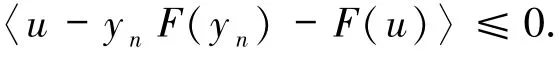
因为u∈SOL（C，F）∩Fix（S），可得

所以

而

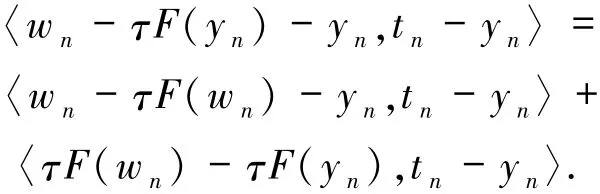
由Tn的定义以及tn∈Tn，可得

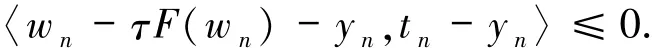
因此

由（10）和（11）式可得

由（6）、（8）、（9）及（13）式有

由（6）式可得

又

经整理后，可得

其中

根据ρn的定义，有

由（19）式以及βn∈（0，1），可得

分别定义序列

结合｛αn｝的单调性和φn≥0，有

由（18）式可得

根据δ和σ的选取以及βn所满足的条件，可以证明

事实上，根据ρn的定义有

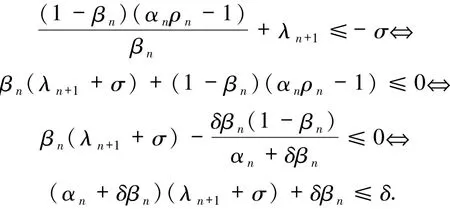
由（20）式知

又因为

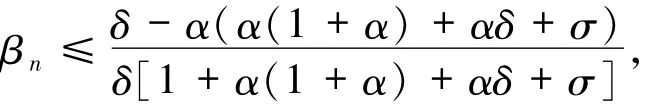
可得（23）式中最右边的不等式成立，因此，（22）式成立.

由（21）和（22）式得

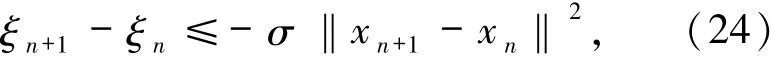
故序列｛ξn｝是非增的.又｛αn｝是有界的，得

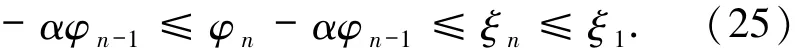
从而有

结合（24）和（25）式，有

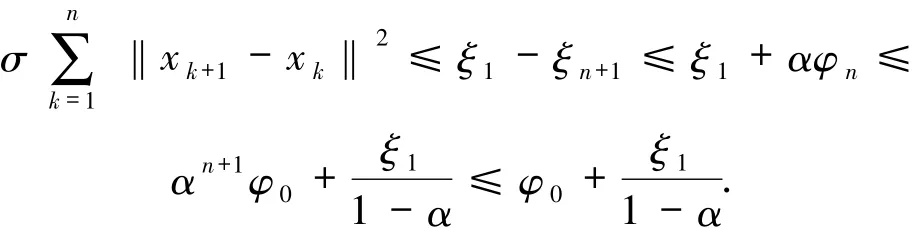
从而

因此

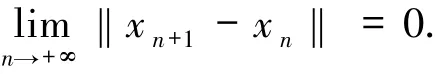
又由（18）式得

因为ρnαn＜1，可得

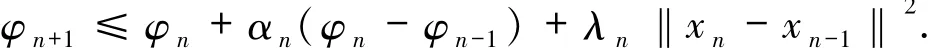
由引理1.4知存在，可推出｛xn｝是有界的.又

由（26）式可得

进而有

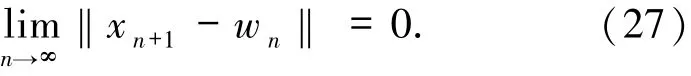
又

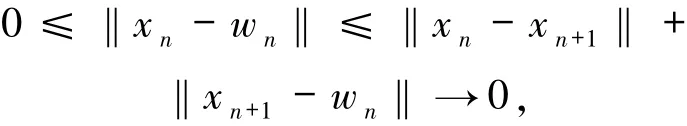
可得

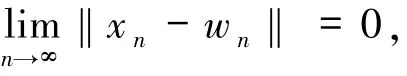
因此，序列｛wn｝也是有界的.

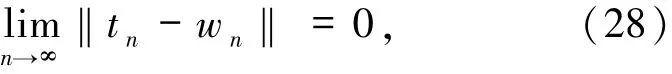
因此，序列｛tn｝也是有界的.由（12）式，可得

由（28）式可得

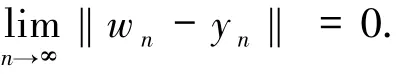
又序列｛xn｝是有界的，则存在子序列｛xn j｝弱收敛于＾x.此外，也可得相应子序列｛wn j｝、｛yn j｝也弱收敛于＾x.

接着证明＾x∈SOL（C，F）∩Fix（S）.定义算子

其中NC（v）称为C在v处的法锥，即

易知A（v）是极大单调算子，且A-1（0）＝SOL（C，F）.

如果（v，w）∈G（A），则w-F（v）∈NC（v），有由yn j∈C，可得

由yn的定义和引理1.1，可得

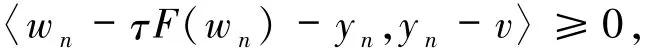
或

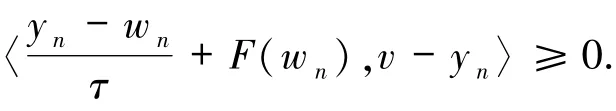
因此，有

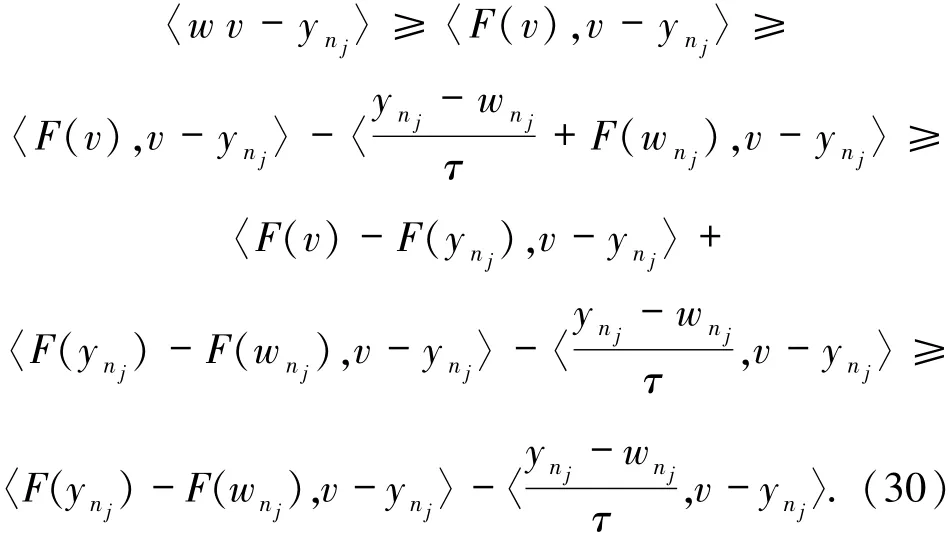
对（30）式两边关于j→∞取极限，得

因A是极大单调的，可得0∈A（＾x），即

又

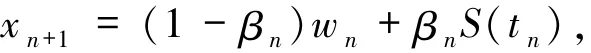
有

由（27）式可得

又

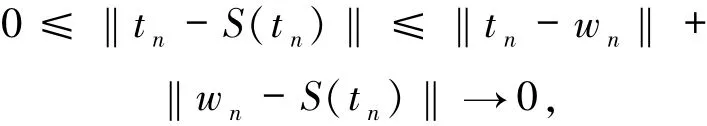
可得

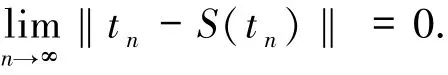
应用引理1.3，有＾x∈Fix（S），故

1）对任意p‖存在；

2）如果xn j⇀p，有p∈SOL（C，F）∩Fix（S）.由引理1.5知｛xn｝弱收敛于SOL（C，F）∩Fix（S）中的一点.

3 数值结果

本节给出算法1和算法2在以下一个简单例子中的计算机检验结果.这些结果都是用Matlab R2017a在CPU型号为Intel（R）Core（TM）i5-3230M（双核，主频为2.60 GHz）和内存为4.0 GB的笔记本电脑上运行的.算法1和算法2选取的参数一致，均取0.4.算法的终止条件为max｛‖wn-tn‖，‖wn-xn+1‖｝≤ϵ，分别取ϵ＝10-4，ϵ＝10-6和ϵ＝10-8作为算法的停止标准.用CPU记运行所花费的时间，用iter记迭代的步数.

例1定义C＝｛x∈R2｜e0≤x≤e1｝，其中e0＝（-10，-10），e1＝（10，10）.设映射F：R2→R2，映射S：R2→R2，

容易证明（详见文献［16］），F是单调且Lipschitz连续的映射.以（1，3）为初始点，通过改变例子中ϵ的取值来对比算法1与算法2，例子的数值结果见表1.

表1 数值结果Tab.1 The numerical result

注2从表1的数值实验结果来看，在相同的精度条件下，算法2迭代的步数比算法1的少，运行所花费的时间也比算法1少.