一种基于椒盐噪声密度的滤波算法

董林鹭， 向 洋， 林国军， 杨平先

（四川轻化工大学自动化与信息工程学院 人工智能四川省重点实验室，四川自贡643000）

图像在传输中受到电磁干扰，使图像产生噪声.其中，椒盐噪声是影响图像信息准确获取的因素之一［1］.特点是随机改变，图像中像素值，使其为暗点或亮点，去除椒盐噪声的研究从未停止过［2-3］.随着滤波技术的发展和工程要求的不断提高，许多学者提出了各种滤波算法［4-7］，如经典中值滤波（MF）［8］计算过程简单、滤波处理速度快，但滤波效果随着噪声密度增加而变差.自适应中值滤波（AMF）［9］利用窗口遍历图像，通过对比窗口内像素值关系，达到滤波效果，同样对于高密度噪声滤波效果较差.针对高密度椒盐噪声，王志军［10］提出一种自适应中值梯度倒数加权的图像滤波算法.该算法自适应调节窗口大小检测出椒盐噪声并进行中值滤波处理，同时通过设定的阈值对高斯噪声进行梯度倒数加权平滑，以达到滤除混合噪声的目的.兰霞等［11］等提出了一种迭代的中值滤波算法，该方法首先依据像素的强度值判断噪声点的位置，然后在循环迭代的处理框架内 对噪声像素进行逐步恢复，但是对复杂模型的噪声效果还不够理想.可知不同算法在不同噪声密度、不同场景下优点和缺点不同.因此，对图像批量处理时预先估计出噪声密度，自适应选取该密度下性能（滤波效果和滤波处理时间）最优的滤波算法，这样才能满足实际工程要求.

结合滤波实际情况，提出了一种基于现有的滤波算法在不同的椒盐噪声的密度下，自适应选取滤波效果较好且滤波处理时间短的算法，对噪声图像进行滤波处理.为了实现该想法，本文提出了一种根据滤波算法，去噪效果和滤波时间的综合评价公式，判断出不同密度下综合性能最优的滤波算法，避免单一滤波算法在处理批量噪声图像时视觉效果与滤波处理时间不能兼顾的矛盾.同时将噪声污染区域单独分离出来处理避免未被污染区域像素集被二次污染，保护图像细节，对于密度过高的椒盐噪声图像该方法保护细节能力相对变弱.

1 滤波算法性能分析

1.1 各滤波算法峰值信噪比、滤波时间的确定不同类型滤波算法根据计算复杂度可分两类.第一类，算法简单处理时间快，但滤波效果较差；第二类，滤波算法复杂滤波效果较好，滤波时间相对较长.本文从滤波效果与滤波处理时间两方面综合考虑后结合滤波性能判定公式，得到各类滤波算法在不同噪声密度下的性能参数.

对噪声图像分别利用加权中值滤波（WFM）、极值中值滤波（EMF）［12］、开关中值滤波（SMF）［13］、自适应中值滤波进行去噪实验，得到滤波算法在不同椒盐噪声密度下，各算法的峰值信噪比和滤波时间，如表1所示.其中，WZ表示未处理的噪声图与原图的峰值信噪比（PSNR）.选取了30幅265×265大小8 bit的标准matlab实验图片作为实验样本，分别加10%～90%密度的椒盐噪声，取峰值信噪比W，运行时间t的平均值进行比较，确定出滤波算法库.信噪比表达式为

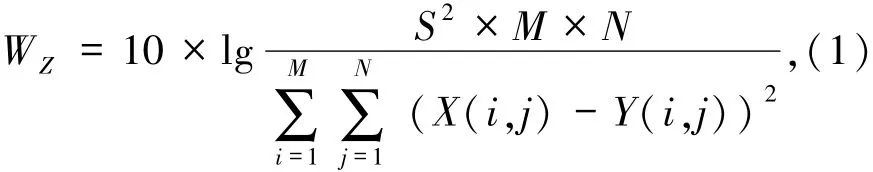
其中，M和N分别为图像横向和纵向的像素个数，X（i，j）为原始图像的灰度值，Y（i，j）为经过滤波器处理后的图像灰度值，S为图像中可能出现的最大灰度值（本文选用灰度级为8位图像，则S＝255），由（1）式可得，当PSNR值越大这滤波图像与原图越接近.

表1 各种滤波算法对30幅图像滤波后的平均PSNR值和t值的比较Tab.1 Comparison of the average PSNR value and t-value after 30 image filtering with various filtering algorithms

1.2 综合评价公式的确定波算法的性能，应同时包含峰值信噪比与滤波时间t两个参数，有的滤波算法在低噪声密度下，峰值信噪比值较高，但处理时间是其他滤波算法的几十倍甚至上百倍，就不能判定该滤波算法性能最优.下面提出一种结合滤波效果与滤波处理时间的判别公式，对滤波算法作出综合评价，表达式

其中，Sn表示滤波算法性能系数，Wn表示图像滤波处理后的PSNR值，WZ表示未处理的噪声图与原图的PSNR值，t表示滤波处理时间.

利用表1数据，从三方面对综合评价公式的合理性进行验证.

1）在相同噪声密度下，取两种滤波算法对其峰值信噪比（PSNR）和滤波时间进行比较.要求其中一种算法的峰值信噪比和滤波时间都要优于另一种.

噪声密度在10%时，WMF的峰值信噪比为27.55、滤波时间为0.051 6.SMF的峰值信噪比为34.17、滤波时间为0.021 4.对比数据，SMF滤波效果和滤波时间都优于WMF，则SMF滤波性能优于WMF.利用综合评价公式求得SMF的性能值为21.85大于WMF的性能值11.76.判断出SMF性能优于WMF.判断结果前后一致.

2）在相同噪声密度下，取两种滤波算法对其峰值信噪比和滤波时间进行比较.要求，其中一种算法的峰值信噪比优于另一种，滤波时间两者接近.

噪声密度在30%时，WMF的峰值信噪比为25.29、滤波时间为0.059 9.SMF的峰值信噪比为28.39、滤波时间为0.055 9.对比数据，在滤波时间接近的情况下，峰值信噪比大的性能较优，则SMF的性能优于WMF.利用综合评价公式求得SMF的性能值为17.89大于WMF的性能值14.16.判断出SMF性能优于WMF.判断结果前后一致.

3）在相同噪声密度下，取两种滤波算法对其峰值信噪比和滤波时间进行比较.要求，其中一种算法的滤波时间优于另一种，峰值信噪比两者接近.

噪声密度在50%时，EMF的峰值信噪比为24.21、滤波时间为0.140 8.SMF的峰值信噪比为24.12、滤波时间为0.105 0.对比数据，在峰值信噪比接近的情况下，滤波时间短的性能较优，则SMF的性能优于EMF.利用综合评价公式求得SMF的性能值为13.84大于EMF的性能值12.94.判断出SMF性能优于EMF.判断结果前后一致.

滤波后的峰值信噪比Wn减去噪声图的峰值信噪比WZ，当两者之差大于0时，证明该滤波算法有去噪效果.当两者之差等于0时，证明该滤波算法没有滤波效果.当两者之差小于0时，表明该滤波算法没有滤波效果，并对原图细节造成二次污染.

在有滤波效果的情况下，时间参数t，其权值由表示，由图1可知，在综合评价公式中，滤波算法处理噪声时间的长短，直接影响性能的优劣.因为，目前的滤波算法，滤波后峰值信噪比的值相差并不明显，为了拉开评价数值的距离，只能利用时间参数得到的权值来综合评价，当无法区别滤波效果的优劣时，在时间权值的作用下，时间相差微毫，能将滤波算法性能的优劣明显区分开.

图1 时间参数在综合评价公式中权值的对应取值函数图Fig.1 The corresponding value function diagram of the weights of time parameters in the comprehensive evaluation formula

由（2）式和图1可知，该综合评价公式，适用于滤波算法对每幅图像的滤波时间小于1 s的情况，如果滤波时间超过1 s，则在实际工程应用中无研究价值.本文采用该公式得出性能值，能客观的筛选出不同密度下的最优滤波算法.

本文仅利用该原理，达到方便快捷的对滤波算法进行筛选的目的.在未来的研究中，重点研究该综合评价公式的合理性.

1.3 不同密度下最优滤波算法的确定规定不同噪声密度下，加权中值滤波性能系数为S1、极值中值滤波性能系数为S2、开关中值滤波的性能系数为S3、自适应中值滤波性能系数为S4.几种滤波的性能系数如表2所示.

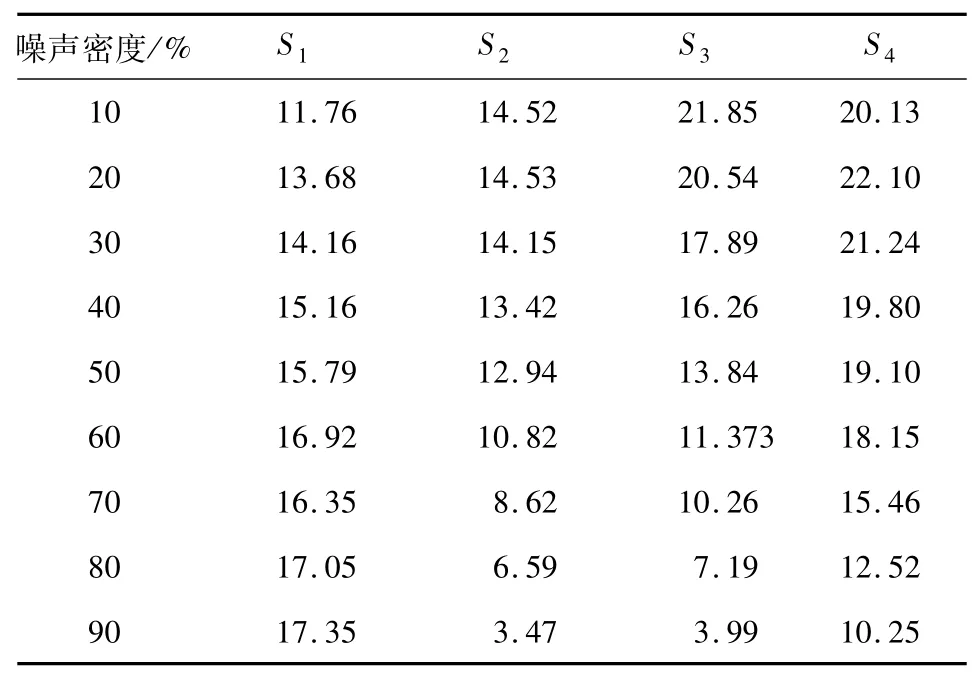
表2 几种滤波算法性能系数比较Tab.2 Comparison of performance coefficients of several filtering algorithms

由表1、表2分析可得，在椒盐噪声密度为10%时，自适应中值滤波峰值信噪比最大，开关中值滤波的峰值信噪比略小于前者，考虑了滤波处理时间t的因素，自适应中值滤波滤波处理时间是开关中值滤波的3倍左右，利用滤波性能评价公式，开关中值滤波在椒盐噪声密度为10%的滤波性能好于自适应中值滤波.为了直观的观察不同椒盐噪声密度下处理性能最优的滤波算法，将表2绘制成折线图，如图2所示.

图2 几种滤波算法的性能系数比较Fig.2 Comparison of performance coefficients of several filtering algorithms

对几种滤波算法去噪研究后，建立不同椒盐噪声密度下，对应的最优性能滤波算法函数的表达式为

2 本文算法

椒盐噪声是图像传输过程中常见的噪声，原理是随机在图像上产生亮（像素值255）暗（像素值0）污染，未被污染的细节像素与原图保持一致.一幅8 bit灰度图被椒盐噪声污染后，图像可分为噪声像素f（i+u，j+u）、细节像素f（i，j），得到噪声图像表达式

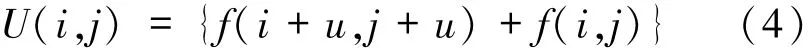
对椒盐噪声图像进行滤波，处理算法可以用现有的任何滤波算法，目的是得到一幅接近于原图的图像，本文采用中值滤波算法，对其预处理得到滤波后图像g（i，j），

利用噪声图像U（i，j）减去滤波处理后的图像g（i，j）得到噪声f（i+u，j+u），其原理是，两图相比，滤波后图像滤除了椒盐噪声，细节像素与原图非常接近，噪声像素值远大于滤波后的像素，这样便分离出噪声f（i+u，j+u）.但原图与滤波后的图像还是有一定的误差，为了避免这样的误差干扰.在处理阶段设立阈值k，因为在滤波过程中，滤波算法会对细节像素造成二次污染，经过大量试验阈值k为25可以减少这样的误差干扰.当

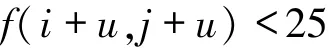
时，令

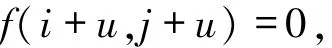
当

时，令

表达式为

利用椒盐噪声特性，求出细节像素f（i，j），表达式为

求出图像所有像素点个数S，再求所有出噪声像素个数S1，根据椒盐噪声特点，利用非噪声像素个数S2间接获得噪声像素个数S1，即求出非噪声像素个数，表达式为

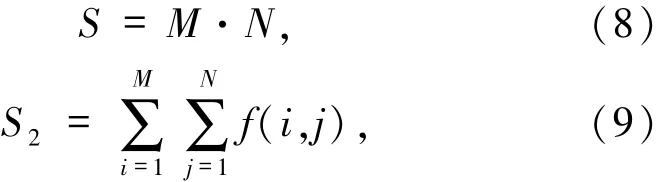
（9）式中，当f（i，j）＞0则f（i，j）＝1，则椒盐噪声密度P估计表达式为

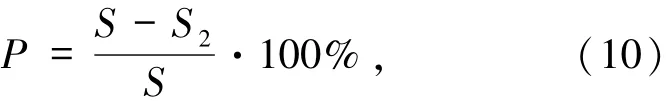
估计出噪声图像密度后，调用已建立的滤波算法与密度的函数式（3），有针对性的对批量噪声图像自适应选取最优性能的滤波算法，进行滤波处理.

利用细节像素f（i，j）与噪声位置像素被滤波后，得到的新像素L（i，j），两者镶嵌融合，使图像细节部分保护的更完整［14-15］，相当于只对噪声像素滤波处理，提高了信噪比（PSNR）和视觉效果，表达式为

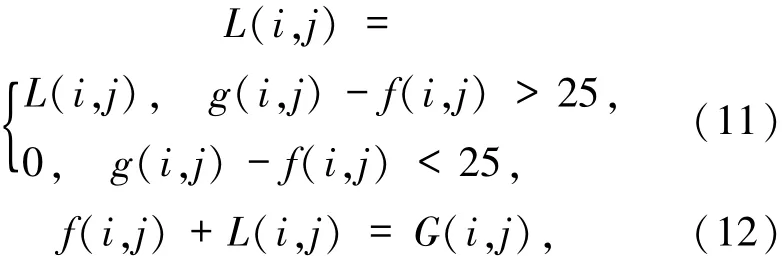
（12）式为批量图像的噪声处理最终输出结果.

3 实验结果讨论

3.1 主观评价首先从图像细节上来验证算法的有效性，为了证明算法的普遍性，选取图片大小为256×263，8 bit的灰度图像，分别加30%的噪声密度和60%的噪声密度，滤波效果图如图3、图4所示.

图3 30%椒盐噪声下去噪结果Fig.3 30% salt and pepper noise denoising results

图4 60%椒盐噪声下去噪结果Fig.4 60% pepper and salt noise denoising results

分析图3和图4可得，椒盐噪声密度为30%、60%时，本文算法所得到的滤波视觉效果是几种滤波算法中最优.观察图3中Einstein实验图像滤波效果，AMF算法滤波效果图有白点，本文算法完全滤去了噪声.相比于选用的滤波算法经过本文噪声分离优化处理后效果更优

3.2 客观评价进一步验证本文算法的有效性.首先验证，本文算法估计出的椒盐噪声密度与实际椒盐密度的误差，再采用了客观的评价函数图像的峰值信噪比与图像的结构相似度（SSIM），对本文算法进行客观评价.其中峰值信噪比的评价原理在前文有详细介绍，对于结构相似度的图像评价原理介绍如下，其表达式：

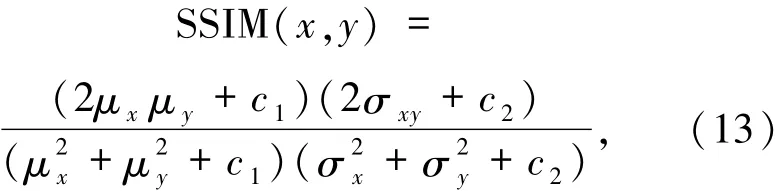
其中，μx是x的平均值，μy是y的平均值是x的方差是y的方差，σxy是x和y的协方差.c1＝（k1L）2，c2＝（k2L）2是用来维持稳定的常数.L是像素值的动态范围.k1＝0.01、k2＝0.03.由（15）式可得，在0到1之间SSIM值越接近1，两张图片结构越相似，当值为1时表示两图完全一致.

本文分别对265×265大小8 bit的灰度图Lena、cameraman、Einstein、woman、baboon加10%到90%的椒盐噪声，用加权中值滤波、极值中滤波、开关中值滤波、自适应中值滤波［15］、和本文算法对图像进行滤波处理，多次试验后取客观评价值的平均值，其中，峰值信噪比用W表示，结构相似度用G表示，如表3所示.

表3中分析可得，本文算法对噪声密度估计准确率非常高，误差在0.1%以内.

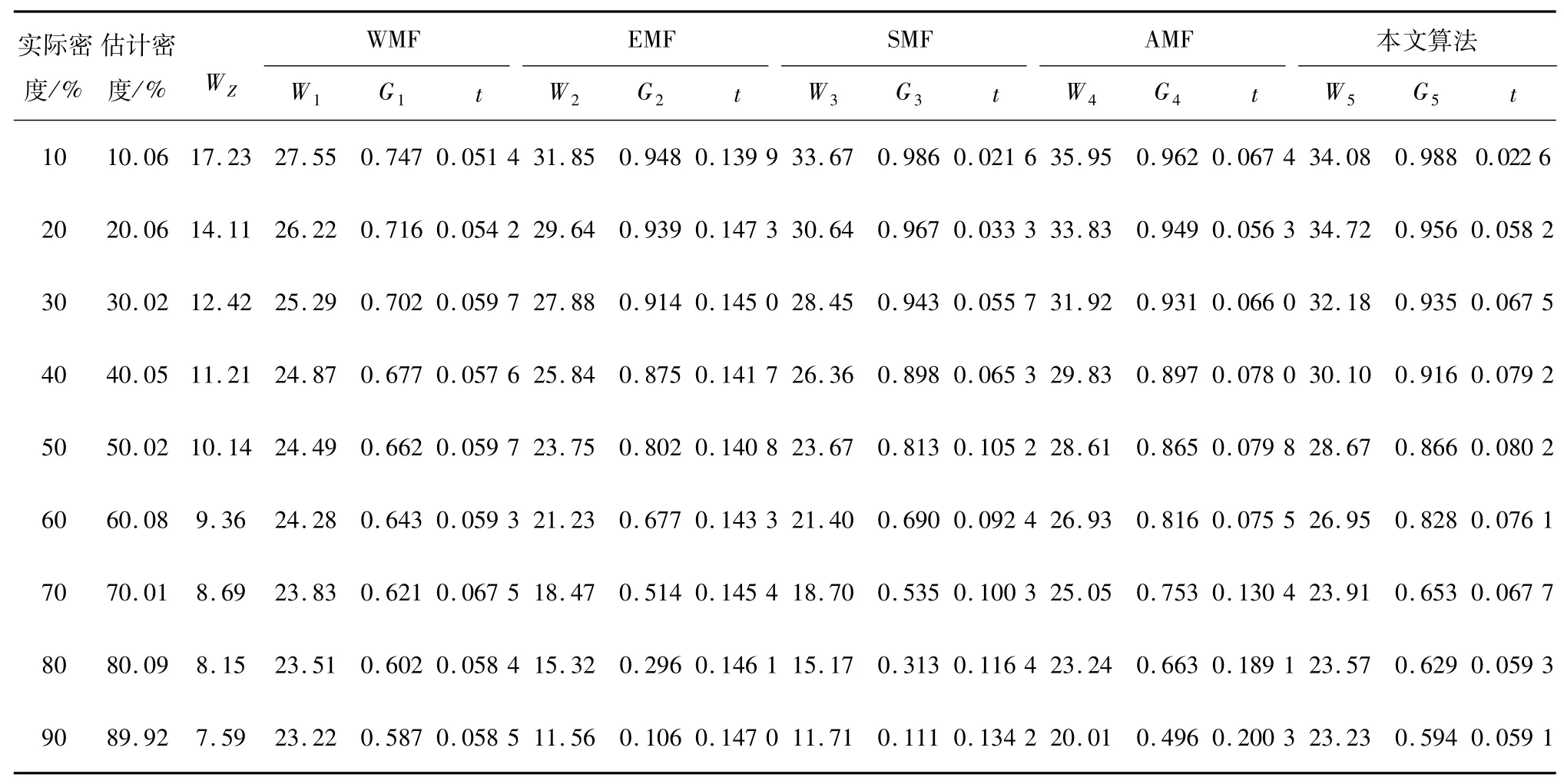
表3 几种滤波算法处理的平均客观评价Tab.3 Average objective evaluation of several filtering algorithms

峰值信噪比和图像相似度值上分析可得，本文算法在椒盐噪声密度为10%、70%时峰值信噪比和结构相似度的值不是最大的，原因有两个，第一本文自适应选用的最优滤波算法是从滤波效果和滤波处理时间综合考虑选取的，因此，在峰值信噪比和结构相似度值相差不大的情况下，选取时间最短的滤波方法，第二本文因篇幅的限制在实验中选取的滤波算法种类过少造成的，但不影响本文思想的表达.将表绘制成折线图，如图6所示.

利用本文提出的滤波性能系数公式，进一步阐述了滤波算法的性能优劣不仅仅是看客观评价值，还要结合滤波处理时间，如表4所示.

图5 几种滤波算法对图像去噪平均PSNR性能比较Fig.5 Comparison of average PSNR performance of several filtering algorithms for image denoising

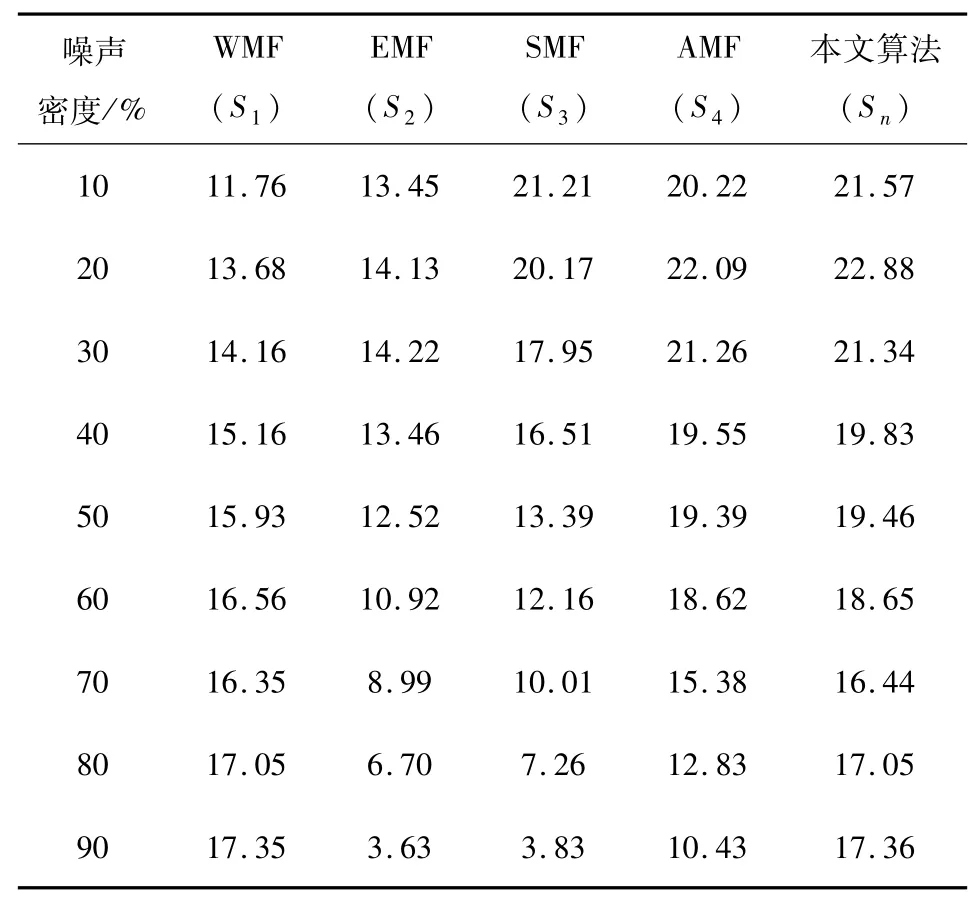
表4 几种滤波算法与本文算法性能系数比较Tab.4 Comparison of performance coefficients of several filtering algorithms and this algorithm

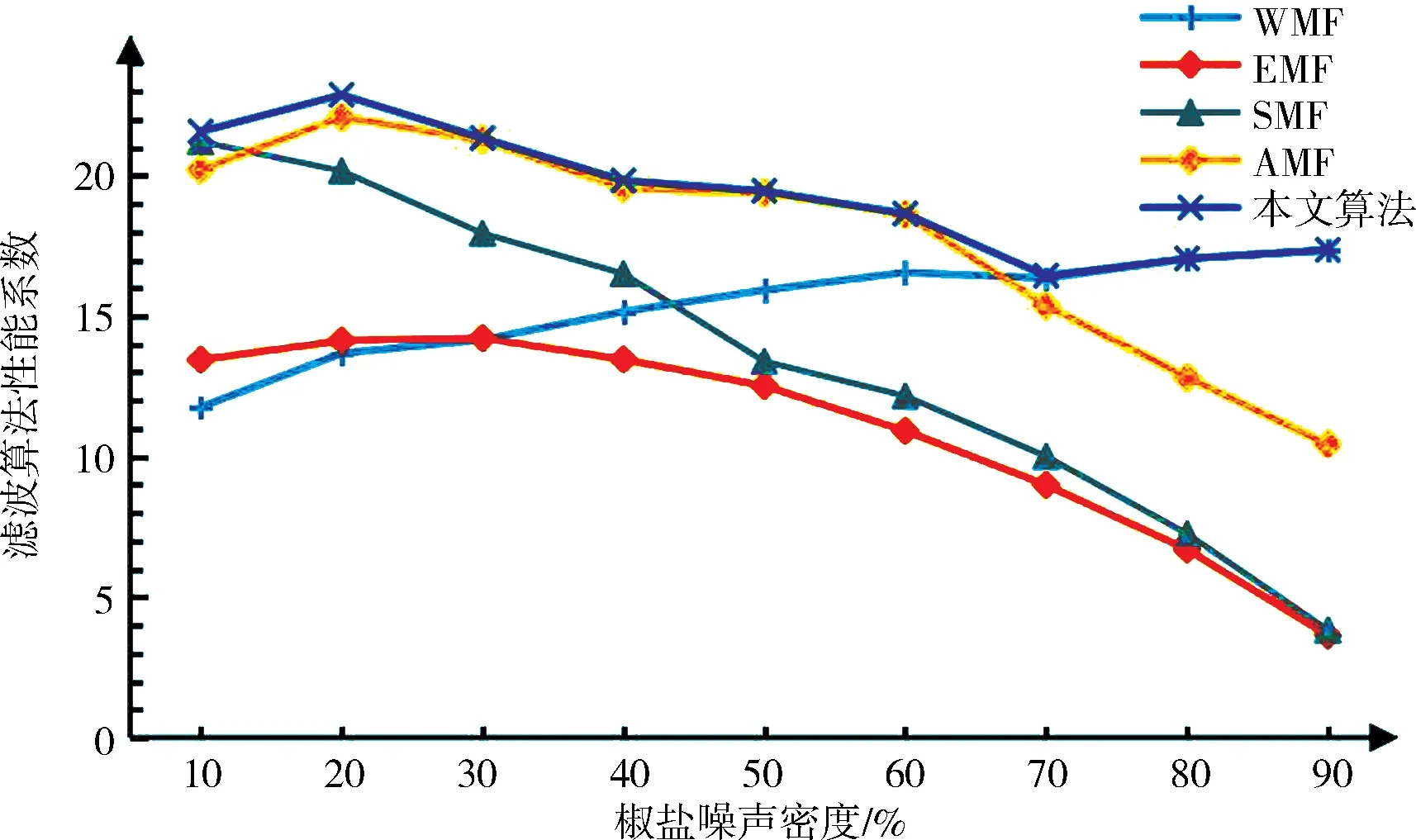
图6 几种滤波算法与本文算法性能系数比较Fig.6 Comparison of performance coefficients of several filtering algorithms and this algorithm

将表4绘制成折线图如图6所示，分析可得，本文算法性能最优，在椒盐噪声密度为10%时，滤波库选取的是开关自适应中值滤波（SMF）性能值为21.12，经过本文的噪声分离处理后性能值提升到21.57，当椒盐噪声密度高达90%时，本文对的噪声分离处理后性能提升只有0.01，随着噪声密度的增加这样的性能提升就会有所降低，后续将重点研究高密度噪声下的优化效果.

4 结论

对批量椒盐噪声图像的去噪过程分析后可知现有的处理技术不能自适应的选取在不同噪声密度时对应的最优滤波算法，造成了滤波效果与滤波时间不能兼顾的矛盾问题，本文提出了基于不同噪声密度下自适应选取性能最优的滤波算法对其滤波处理.实验结果表明，本文算法在噪声密度估计过程中所耗时间非常短，并且噪声估计精度较高，同时利用噪声分离技术保护了图像细节，实际工程意义较大.

致谢四川理工学院科研项目（2015RCA9）对本文给予了资助，谨致谢意.