交换半环上半模的标准基
周艺璇, 王学平
(1.四川民族学院理工学院,四川 康定626001; 2.四川师范大学数学科学学院,四川 成都610066)
半环上半模理论的研究历史悠久.1966年,Yusuf[1]提出半环上可逆半模的概念,并得到类似于模理论的定理.于是,很多学者以此为起点展开对半模理论的研究[2-4].如:文献[2]广泛地描述半环以及半环上的半模,并介绍半模理论在数学的其他分支、密码学及理论计算机科学等上的应用;文献[5-6]讨论零和自由半环上可逆矩阵的性质,完善了半可逆矩阵的性质,扩展了矩阵的应用范围;文献[7]描述了有极小理想的半环的结构.
基是半模中最重要的概念,由此国内外学者关于基的研究工作很多,如:文献[3]在MV代数上建立了半线性空间,引入基的概念,并提出在半线性空间中不同基的势是否相等的开问题;文献[8]在join-半环中给出不同基的势相等的充要条件;文献[9]给出Zerosumfree半环上n维半线性空间Vn中每组基有相同势的充要条件;文献[10]探讨了交换的Zerosumfree半环上n维半线性空间Vn的标准正交向量,并给出向量集成为正交向量组生成的半线性空间的基的充要条件;文献[11-12]对交换半环的基和基数展开了深入的讨论;文献[13]引入自由基的概念,探讨交换半环上半模的基的基本性质及其特征,并给出了交换半环上有限生成自由半模的基为自由基的充要条件;文献[4]研究了交换半环上半模的自由集和自由半模.从已有的研究工作不难发现,按现有半模上基的概念,不同基的势要相等需要条件,文献[13]引入的自由基也是有条件的,这就限制了很多半模.为此,本文提出了标准基的概念,并以此为基础,将标准基与自由基做对比,讨论标准基的基本性质.
1 预备知识
下面回忆一些基本概念及已有结论.
定义1.1[2,14]设L是非空集合,若代数结构L=〈L,+,·,0,1〉满足:
1)(L,+,0)是交换幺半群;
2)(L,·,1)是幺半群;
3)∀r,s,t∈L,r·(s+t)=r·s+r·t与(s+t)·r=s·r+t·r成立;
4)∀r∈L,0·r=r·0=0成立;
5)0≠1;则称L为半环.
特别地,若对∀r,r′∈L,都有r·r′=r′·r,则称L为交换半环.
定义1.2[2,14]设L=〈L,+,·,0,1〉为半环,A=〈A,+A,0A〉为交换幺半群.若外积*:L×A→A满足:∀r,r′∈L,a,a′∈A,
1)(r·r′)*a=r*(r′*a),
2)r*(a+Aa′)=r*a+Ar*a′,
3)(r+r′)*a=r*a+Ar′*a,
4)1*a=a,
5)0*a=r*0A=0A,则称〈L,+,·,0,1;*;A,+A,0A〉为左L-半模.类似可给出右L-半模的定义.
也称半环L上的半模为L-半线性空间[13],这里的半模或是左L-半模,或是右L-半模.
例1.1设L=〈L,+,·,0,1〉是半环.对n≥1,令

其中(a1,a2,…,an)T表示(a1,a2,…,an)的转置.对任意的x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T∈Vn(L)和r∈L,定义

则

是L-半线性空间,其中

设

类似地,按照以上方法定义运算“+”和“*”,则
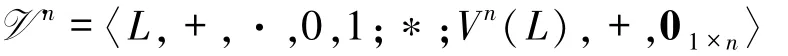
是L-半模,其中

在不会引起混淆的情况下,在L-半模〈L,+,·,0,1;*;A,+A,0A〉中,对任意的r∈L,α∈A,将用rα代替r*α.
设N为L-半模M的非空子集,若N在加法和数乘运算下封闭,则称N为M的子半模.显然,若是M的一族子半模,则也是M的子半模.
令S为L-半模M的非空子集,则所有包含S的M的子半模的交是M的子半模,称其为由S生成的子半模,并用符号LS表示.容易验证
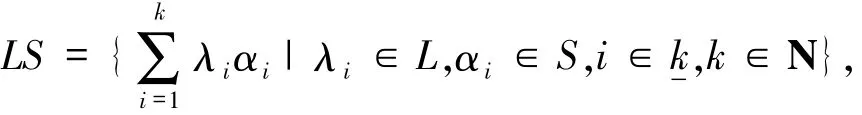

则
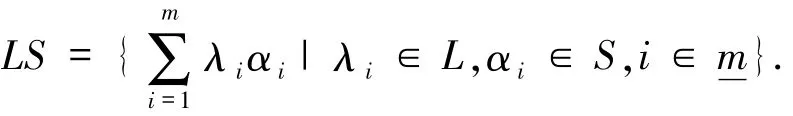
特别地,若S={α},则用Lα定义LS,即

若LS=M,则称S为M的生成集.进一步,若S为有限集,则称该半模为有限生成的.定义L-半模M的最小的生成集的势为L-半模M的秩,并用符号r(M)表示.显然,任何有限生成的L-半模M的秩r(M)都存在.
定义1.3[2,13]设S是L-半模M的非空子集,若对任意的α∈S,α∉L(S\{α}),则称S是线性无关的.否则,称S线性相关.如果L-半模M的元至多能被非空子集S中元以一种方式表出,则称S是自由的.
显然,自由集一定是线性无关的.
定义1.4[2,13]称L-半模M中线性无关的生成集为M的基.特别地,称L-半模M的自由生成集为自由基.称有自由基的L-半模M为自由的.
例1.2例1.1中的L-半模Vn是有限生成的自由的L-半模.{e1,e2,…,en}是Vn的自由基,其中,e1=(1,0,…,0)T,e2=(0,1,…,0)T,…,en=(0,0,…,1)T.显然,r(Vn)=n.易见,Vn也是有限生成的自由的L-半模,且r(Vn)=n.
设下文中的M均为交换半环上有限生成的L-半模.
2 自由基的性质
设T1,T2,…,Tn是L-半模M的n个L-子半模.定义T1,T2,…,Tn的和如下:
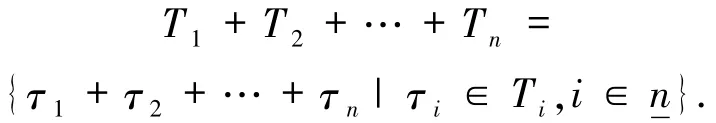
显然,T1+T2+…+Tn是L-半模M的L-子半模.设T=T1+T2+…+Tn,若对任意向量ν∈T,都存在唯一的使得

则称M的L-半模T为T1,T2,…,Tn的直和,记作

定理2.1设V1与V2是M的2个L-子半模,{γ1,γ2,…,γs}和{η1,η2,…,ηp}分别是V1和V2的自由基,则V1+V2=V1⊕V2当且仅当任意α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示.
证明充分性 对任意α∈V1+V2,设

其中,α1,β1∈V1,α2,β2∈V2.于是存在ki,k′i,lj,使得

因此

由于α∈V1+V2可唯一的由γ1,γ2,…,γs,η1,η2,…,ηp线性表示,因此

从而

也就是说

必要性 对任意α∈V1+V2,设

其中,ki,k′i,lj,lj′∈L.因为

所以
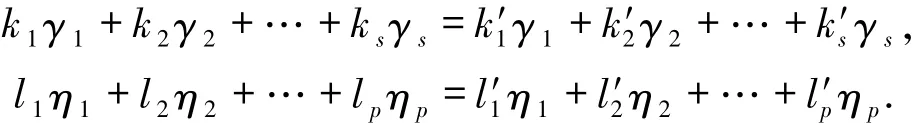
又{γ1,γ2,…,γs}和{η1,η2,…,ηp}分别是V1和V2的自由基,因此ki=k′i,lj=l′j.即,任意α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示.
注2.1定理2.1推广了文献[15]中定理3.1.
为了说明注2.1,首先回忆标准正交的概念[16].
设M为L-半模,若对任意的α,β,γ∈M,λ,μ∈L,满足:
1)〈α,β〉=〈β,α〉;
2)〈λα+μβ,γ〉=λ〈α,γ〉+μ〈β,γ〉;
则称M×M→L的二元运算〈,〉为M上的内积运算.
设U(L)={a∈L|存在b∈L使得ab=ba=1}.再设A是L-半模M的非空子集,若对任意α,β∈A,α≠β,有
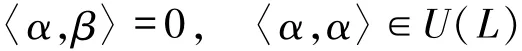
成立,则称A是标准正交的.
引理2.1[16]设A={α1,α2,…,αn}是M的标准正交集,则A自由.
由引理2.1即知L-半模M的标准正交集一定是自由的,但自由的向量集不一定是标准正交的.
例2.1设α=(a1,a2,…,an)T,β=(b1,b2,…,bn)T∈Vn,定义
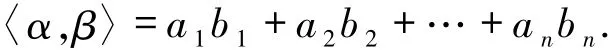
易见〈,〉为半模Vn的内积,又称为Vn上的标准内积.
例2.2考虑模8的剩余类环

易见(0,0,1)T、(0,1,1)T、(1,1,1)T是V3的自由基,但按标准内积显然不是标准正交的.
由定理2.1及其证明易见下面定理成立.
定理2.2设V1与V2是M的2个L-子半模,{γ1,γ2,…,γs}和{η1,η2,…,ηp}分别是V1和V2的自由基,则V1+V2=V1⊕V2当且仅当{γ1,γ2,…,γs,η1,η2,…,ηp}是V1+V2的自由基.
定义2.1定义半模的秩为半模的维数.半模M的维数用符号dim M表示.
注2.2上面维数的定义与经典线性代数中维数的定义是一致的,但与文献[9]中维数的定义不同.
例2.3设L是非负整数连同运算
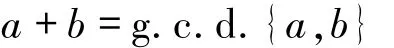
和

构成的半环,其中g.c.d.{a,b}表示a与b的最大公因数,l.c.m.{a,b}表示a与b的最小公倍数.在L-半模V2中,向量组{(0,1)T,(1,0)T}、{(2,0)T,(3,0)T,(0,2)T,(0,3)T}都是V2的基.在定义2.1下,dim V2=2.但在文献[9]的定义下,维数是不存在的.
引理2.2[13]设M是有限生成的自由的R-半模,则对其任意基S和任意自由基T都有

推论2.1设V1与V2是M的2个L-子半模,{γ1,γ2,…,γs}和{η1,η2,…,ηp}分别是V1和V2的自由基.若

则
1)dimV1+dimV2=dim(V1+V2);
2)V1∩V2={0}.
证明1)由定理2.2及引理2.2易知结论成立.
2)设α∈V1∩V2,于是存在ki,k′i,lj,lj′∈L,使得

因此

而由定理2.2可知{γ1,γ2,…,γs,η1,η2,…,ηp}是V1+V2的自由基,于是

从而α=0.
推论2.2设V1与V2是M的2个L-子半模,{γ1,γ2,…,γs}和{η1,η2,…,ηp}分别是V1和V2的自由基.若α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示,则V1∩V2={0}.
证明由定理2.1及引理2.1易知结论成立.
定理2.1、定理2.2、推论2.1以及推论2.2都只讨论了2个子半模的情况.事实上,在n个子半模上也有类似的结论,并且其证明过程也是类似的.
定理2.3若{γ1,γ2,…,γs}是L-半模V的自由基,则
〈γ1〉+〈γ2〉+…+〈γs〉=〈γ1〉⊕〈γ2〉⊕…⊕〈γs〉.
证明假设存在使得
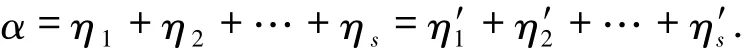
不妨设


由{γ1,γ2,…,γs}自由可知ki=k′i,从而ηi=η′i,即

3 L-半模的标准基
定义3.1称L-半模M中向量个数最少的基为标准基.
显然,任意有限生成的L-半模M都有标准基.
注3.1秩为r(M)的L-半模M中任意r(M)个线性无关的向量不一定为M的基,更不一定为标准基.
例3.1已知布尔格B2={0,σ1,σ2,1},其中σ1、σ2为B2的原子.0、1分别为B2的最小元和最大元.显然〈B2,+,·〉是交换环,其中“+”=∨,“·”=∧.考虑B2-半模V3.设
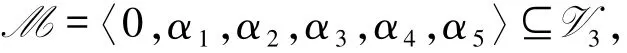
其中

则M是有限生成的B2-半模,它的基分别为:

显然,一个向量不能成为M的基.因此,r(M)=2.显然α1与α3线性无关,但{α1,α3}不是基,更不是标准基.
由引理2.2即知L-半模M的自由基一定是标准基,但标准基不一定是自由基.
例3.2例3.1中M的所有基都不是自由的,从而M无自由基,但T1、T2、T3为M的标准基.
设L是半环,定义Mm×n是L上的m×n阶矩阵的集合.特别地,令
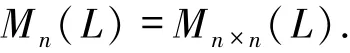
对任意的定义


容易验证,〈Mn(L),+,·,0,In〉是半环,其中0为n×n零矩阵,In为n×n单位矩阵.
以下先回忆可逆矩阵的概念[17].
设A∈Mn(L),如果存在矩阵B∈Mn(L)使得AB=In,则称矩阵A是右可逆的;类似地,可定义左可逆矩阵.如果矩阵A既是左可逆的又是右可逆的,则称A是可逆矩阵.
引理3.1[17]设L是交换半环,A,B∈Mn(L).若AB=In,则BA=In.
定理3.1若M是有限生成的自由的L-半模,A={α1,α2,…,αn}为M的标准基,则A也是M的自由基.
证明由引理2.2与定义3.1可设B={β1,β2,…βn}为M的自由基,于是存在A∈Mn×n(L)与B∈Mn×n(L)使得
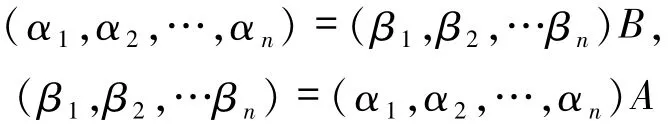
成立,从而有

因为B是自由的,所以BA=In.由引理3.1可知B可逆.现设

其中ki,λi∈L,且则

于是

因为B是自由的,所以

又因为B可逆,所以
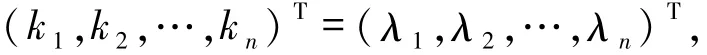
从而A自由.
注3.2定理3.2中L-半模M是自由的条件一般不能去掉.
例3.3在例3.1中,L-半模M是有限生成的,M不是自由的.T1、T2、T3为M的标准基,但不是自由基.
推论3.1若M是有限生成的自由的L-半模,则A={α1,α2,…,αn}是M的标准基的充要条件是A是M的自由基.
定理3.2设M是有限生成的L-半模,{α1,α2,…,αn}是M的一组标准基.若存在可逆矩阵

使
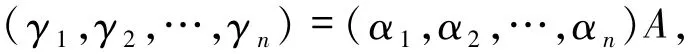
则{γ1,γ2,…,γn}是M的标准基.
证明设B是A的逆矩阵,则
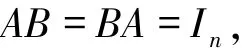
从而有
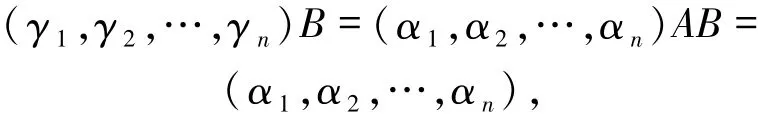
于是{γ1,γ2,…,γn}与{α1,α2,…,αn}可相互线性表出,也就是说{γ1,γ2,…,γn}也是M的生成集.显然{γ1,γ2,…,γn}线性无关,否则与标准基的向量个数为n相矛盾,即是说{γ1,γ2,…,γn}是基.于是,{γ1,γ2,…,γn}是标准基.
注3.3定理3.2的逆命题不一定成立.
例3.4在例3.2中,T1={α1,α4},T2={α2,α3}均为M的标准基.容易得到但均不可逆.
4 标准基的性质
设M和N是L-半模,若映射φ:M→N满足以下条件:
1)对任意的α,β∈M,

2)对任意的α∈M,λ∈L,φ(λα)=λφ(α);则称φ为L-同态映射.若φ是满射,则称φ为满同态映射;若φ是双射,则称φ为同构映射[2],并记为M≅N.
定理4.1设M与M′是2个有限生成的L-半模,φ:M→M′是同构映射,则{α1,α2,…,αn}是M的标准基当且仅当{φ(α1),φ(α2),…,φ(αn)}是M′的标准基.
证明设{α1,α2,…,αn}是M的标准基,α′∈M′,则由φ是满射知存在α∈M使φ(α)=α′.因此存在使得

由于φ同构,于是
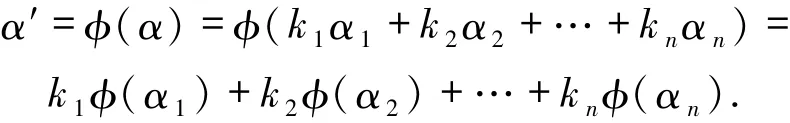
于是{φ(α1),φ(α2),…,φ(αn)}是M′的生成集.再由φ同构容易证明{φ(α1),φ(α2),…,φ(αn)}是M′的标准基.
反之,设{φ(α1),φ(α2),…,φ(αn)}是M′的标准基,α∈M,于是φ(α)∈M′.因此存在

使得有
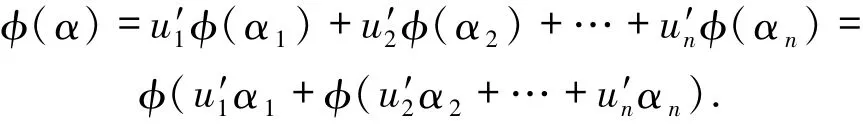
于是

所以{α1,α2,…,αn}是M的生成集.再由φ同构容易证明{α1,α2,…,αn}是M的标准基.
由定理4.1及秩的定义易见下面推论成立.
推论4.1设M、N是2个有限生成的L-半模,若M≅N,则r(M)=r(N).
注4.1推论4.1的逆命题不一定成立.
例4.1在例3.1中,令
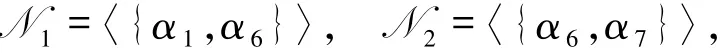
其中

则r(N1)=2=r(N2).显然有N1与N2不是同构的.
但我们有下面定理.
定理4.2设M、N是2个有限生成的L-半模,若r(M)=r(N)且N是自由的,则M≅N.
证明设A={α1,α2,…,αn}是M的标准基,A′={α′1,α′2,…,α′n}是N的自由基.定义φ:M→N满足任意

由A′是N的自由基,易见φ是M到N的映射.设
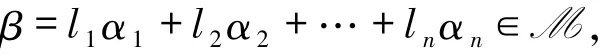
其中li∈L,则

从而φ是同态映射.对任意
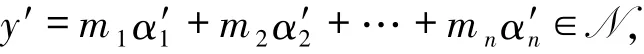
令=

则有φ(y)y′,从而φ是满射.设
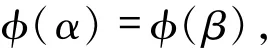
则
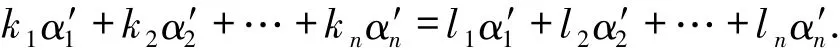
由于{α′1,α′2,…,α′n}自由,所以ki=li,于是α=β,从而φ是单射.综上,M≅N.
定理4.3设V1、V2是M的2个L-子半模,{γ1,γ2,…,γs}、{η1,η2,…,ηp}分别是V1、V2的标准基.如果任意α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示,则:
1){γ1,γ2,…,γs,η1,η2,…,ηp}是V1+V2的标准基;
2)V1+V2=V1⊕V2;
3)dimV1+dimV2=dim(V1+V2);
4)V1∩V2={0}.
证明1)由任意α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示可知{γ1,γ2,…,γs,η1,η2,…,ηp}是V1+V2的自由基,从而{γ1,γ2,…,γs,η1,η2,…,ηp}是V1+V2的标准基.
2)由定理2.1充分性的证明过程易知结论成立.
3)由于{γ1,γ2,…,γs}是V1的标准基,于是dimV1=s.同理,dimV2=p.又由1)的结论,于是dim(V1+V2)=s+p.从而结论成立.
4)设α∈V1∩V2,于是存在ki,k′i,lj,l′j∈L,i∈s,j∈p,使得

因此


由于α∈V1+V2可唯一地由γ1,γ2,…,γs,η1,η2,…,ηp线性表示,所以

从而α=0.

