HPM视角下“无穷级数概念引入”的教学

◇上海立信会计金融学院统计与数学学院 李 玲

上海海洋大学工程学院 成国庆

无穷级数是微积分中的一个重要概念，它体现了无限与有限的辨证统一，在自然科学、工程技术等领域发挥着重要的作用。本文主要从数学史与数学教育（History & Pedagogy of Mathematics，HPM）的视角，以发生教学法为基础，设计了“无穷级数概念引入”的教学，整个过程环环相扣，不断激发学生的求知欲望。实践表明，HPM视角下的无穷级数教学有助于学生对其概念的理解和敛散性判别方法的掌握。

无穷级数是《高等数学》的一个重要组成部分，它可以用来表示函数、研究函数的性质及进行数值计算。无穷级数在自然科学、工程技术等领域发挥着重要的作用，它的一个重要应用—近似求值，正是贯穿于整个高等数学内容的极限思想方法的充分体现。然而，在“重应用”的背后却隐藏着“轻概念”的忧患。级数概念涉及极限思想，“无穷”、“极限”这些曾经让古希腊人惧怕的概念，在当今的高等数学教学中也很容易被教师忽视。然而，“无穷级数”的概念在微积分中的作用不容忽视，它体现了无限与有限的辨证统一，有助于学生理解极限思想，为学生更好地学习微积分打下良好的基础。

基于此，笔者研究了如何将数学史[1]融入到级数概念的教学中，并主要围绕以下3个研究问题展开：①在教学过程中融入数学史，是否有助于学生更好地理解级数中的极限思想？②学生是否乐于接受这种融入数学史的教学方式？③在教学过程中融入数学史与直接使用数学史的主要区别是什么？

1 历史与认知

1.1 无穷级数概念的历史分析

无穷级数曾在希腊数学里出现过，尽管希腊人很惧怕无穷，并且试图用有限和来代替无穷和，但这些只是潜无穷与实无穷的差别。芝诺[2]（Zeno of Elea，约公元前490～约公元前425）的二分法涉及把1分解成这样一个无穷级数：亚里士多德（Aristotle）也认为这种公比小于1的等比级数有和。阿基米德[3]（Archimedes，公元前287一公元前212）在其《抛物线图形求积法》一书中，使用了等比级数求抛物线弓形面积，并给出了它的和。中国古代《庄子·天下》一书中的“一尺之棰，日取其半，万世不竭”也含有极限的思想，其用数学形式表达出来也是无穷级数。

在中世纪，无穷级数一度使那时的哲学家与数学家着迷，一方面引起了他们对“无穷”的兴趣，另一方面又使他们围绕一些明显的悖论展开激烈的争论。例如，休塞特[4]（Richard Suiseth或Swineshead）曾解决了这样一个问题，它可以借助于运动这样描述：

若一质点在某段时间的前一半以不变的初始速度开始运动，在接下来的四分之一时间中以二倍的初始速度运动，而在随后的八分之一时间中以三倍的初始速度运动，……，就这样无限继续下去，则这个质点在整个这段时间的平均速度等于其初始速度的二倍。如果把这段时间的长度和初始速度都取作一个单位，则该问题等价于这样一个级数求和

奥雷姆[5]是这方面最杰出的代表人物。他有着许多天才的思想，尤其是“无穷”的思想。他明确了等比级数有两种可能性，当其公比大于或等于1时，无穷等比级数有无穷和；而当公比小于1时有有限和。在《欧几里德几何问题》（1350）一书中，他用严格的方式证明了当无穷级数项的值不是按比例减少时，其和也能是无穷，并在书中用调和级数作为例子进行了探讨。

此后，无穷级数的研究在十五、十六世纪继续以休塞特和奥雷姆的方式前行，但由于其方式仅限于文字叙述和几何方法，因此没有取得重大的进步。无穷级数早期研究工作的主要贡献不在于所得到的具体结果，而在于它能促使人们接受一种新的观点，那就是在数学中可以自由承认无限过程。因此，中世纪更有力的算术和代数方法为十七世纪关于无穷级数以及无限过程的重要工作开辟了新的道路。

1.2 学生的认知起点

为了把握学生的认知水平，了解大一学生对于无穷多个数相加的概念的了解程度，我们对学习《高等数学》的部分学生作了此概念的问卷调查，问卷中主要涉及以下几个问题：

问题二：根据问题一中计算的结果，请回答无穷多个数相加是否一定会得到一个数，即无穷多个数相加是否存在和；如果有和，这个和是否一定唯一？

对于问题一，参与调查的326名学生给出了以下几种不同的答案，为了更清晰地看出这一调查结果现将其列入表1。

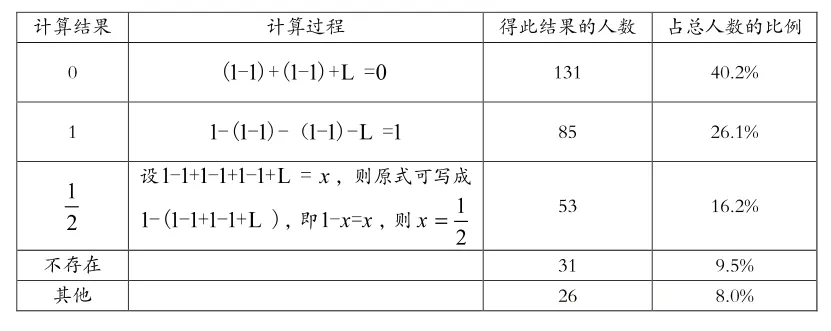
表1 问题一的调查结果

对于问题二，有184名学生认为答案是肯定的，这一数字超过了参与调查人数的一半；而且由于问题一的计算结果，导致认为有和的大部分学生都觉得这个和不一定是唯一的。在参与调查的326人中，只有10人给出了该问题的正确答案。

由以上结果可以看出，学生对于无穷多个数相加是否存在和这一问题概念模糊。在问题一的解答过程中，大部分学生犯了这样几个错误：

（1）将有限个数相加满足的结合律（相加过程中任意添加括号）直接照搬到无限个数相加，这就导致了计算结果0和1的产生；

（2）将有限个数相加一定存在和这一结论直接照搬到无限个数相加，第三种计算过程中，实际已经承认为一个数，进而把它设为x，然后列方程进行求解。

以上两种错误都体现了学生对于从有限个数相加到无限个数相加这一过渡的认知存在误差，这一认知误差也为我们更好地设计教学过程提供了理论基础。

1.3 教学设计意图

（1）以历史上著名的芝诺悖论作为此次教学的序幕，可将学生带入一个熟悉而又陌生的领域，让学生对于即将讲解的数学概念产生兴趣。

（2）在学生充满求知欲的氛围中恰到好处地给出无穷级数的概念，让学生的一部分好奇心得到满足，并由此产生新的疑问：无穷级数何时存在和？

（3）无穷级数敛散性的判别方法呼之欲出，学生终于明白无限多个数相加不一定有和，因此对相关概念以及判别方法理解得更加透彻。

（4）趁热打铁，利用几个典型的例题让学生巩固无穷级数的概念和敛散性的判别方法，并由此解释之前产生的疑问，真正做到举一反三。

（5）当学生感到一切问题都迎刃而解时，提出新的思考，使学生再次产生求知的热情，对后续的教学内容充满期待。

2 教学设计

2.1 一个有意思的悖论

（1）向学生讲述一个历史上著名的芝诺悖论（Zeno's paradox）。

阿基里斯是古希腊神话中一位善跑的英雄。在他和乌龟的竞赛中，他的速度是乌龟的十倍，乌龟在其前面100米跑，他在后面追，但他却不可能追上乌龟。因为在竞赛过程中，追者必须首先到达被追者的出发点，当阿基里斯追到100米时，乌龟又向前爬了10米，这样，一个新的起点就产生了；于是阿基里斯必须继续追，而当他追上这10米时，乌龟又向前爬了1米，阿基里斯只能再追那个1米。一直这样下去，乌龟就会制造出无穷个起点，并且它总能在新的起点与自己之间制造出一个距离，不管这个距离有多么小，只要乌龟不停地奋力向前爬，阿基里斯就永远追不上乌龟。

如图所示，开始时阿基里斯位于A点，乌龟位于B点，阿基里斯速度是10m/s，乌龟速度是1m/s，乌龟在前面100m。当阿基里斯到达B点时，乌龟又向前爬行了10m，到达C点；当阿基里斯到达C点时，乌龟又向前爬行了1m，到达D点……

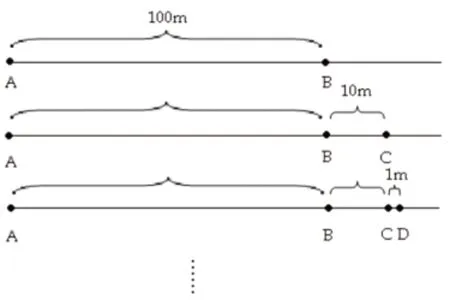
图1 阿基里斯追乌龟的图示

（2）向学生提问并与学生进行互动。

问题：你认为阿基里斯最终能不能追上乌龟？为什么？

问题提出后，学生们都表现得很活跃，觉得这是一个显而易见问题，都认为阿基里斯最终能追上乌龟，但问其原因时，答案却不是那么显而易见了：

学生一的回答：若慢跑者在快跑者前一段，则快跑者一定会追上慢跑者，这是常识；

老师的反问：我认为快跑者永远赶不上慢跑者：因为追赶者必须首先跑到被追者的出发点，而当他到达被追者的出发点，慢跑者又向前了一段，又有新的出发点在等着它，有无限个这样的出发点。

学生二的回答：阿基里斯一定能追上乌龟，因为我可以算出他追乌龟所用的时间，这就是我们小学做过的追及问题：设他追上乌龟用的时间为x，则可列方程：

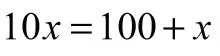
老师的反问：你在假设他追上乌龟用的时间为x时，已经认为他追上了乌龟，因为只有当x是一个有限数（追及时间有限，即表示能追上）时，列的方程才有意义，才能进行求解。而现在的问题是，为什么他追及的时间是个有限值？

经过两轮的互动，学生们对这个看似简单又充满迷惑的问题产生了浓厚的兴趣，阿基里斯到底能否追上乌龟呢？

2.2 无穷级数概念的引入

在这个悖论中，最关键的就是阿基里斯追乌龟所用的时间，而这个时间可以表示为：

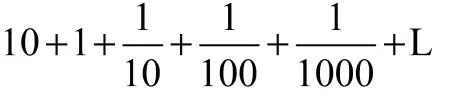
这是无限多个数相加，如果相加得一个有限数（存在和），则他追乌龟所用的时间是有限的，表示他能追上乌龟；反之，如果相加不是一个有限数（不存在和），则表示他不能追上乌龟。

这时，学生对于无穷多个数相加以及是否存在和产生了想继续了解的动机，此时可以给出无穷级数的概念。给出无穷级数的准确定义之后，学生明白了就是一个无穷级数，但这个无穷级数有没有和呢？

2.3 无穷级数的敛散性

有了无穷级数的定义，学生们现在关心是它何时存在和（收敛）。此时可以给出无穷级数敛散性的概念以及判别敛散性的方法。紧接着用两个例题来巩固此判别方法。

2.5 后续的思考

学生们会发现对于这个形式简单的级数，要用常规的方法（部分和数列的敛散性）来判别敛散性并不是那么容易，在下节课可以给学生介绍一种更巧妙的方法判断其敛散性。

3 学生反馈

此次教学后，我们对所教六个班中的18名学生进行了访谈，其中涉及的问题有：①通过这次教学，你能更好地理解无穷级数的概念吗？②你能说出几个常见的无穷级数吗？③你知道如何判别无穷级数的敛散性吗？④你觉得这节课有趣吗？

在整章教学完成后，我们又对这六个班级326人进行了关于这次教学的问卷调查，其中涉及的问题有：①此次教学对于你理解无穷级数的概念作用大吗？②此次教学对于你整章内容的学习作用大吗？③你能否接受这种将数学史融入数学教学的方法？④你是否希望在今后的教学过程中，老师经常使用这种方法？

3.1 访谈结果

接受访谈的学生一致认为此次教学很有趣、很生动，已经能很好地理解无穷级数的概念，并且知道了无限个数相加与有限个数相加的本质区别：无限个数相加不一定有和。另外，大部分受访学生都能说出几个常见的级数，如等比级数，调和级数等。他们普遍认为这节课的精彩之处在于阿基里斯追乌龟这个悖论的出现，让他们至始至终对无穷级数的概念及其敛散性充满了好奇和求知的欲望，因此对整个教学过程印象深刻。

3.2 问卷调查结果

表2给出了学生对于以上几个问题的回答情况。

表2 学生对此次教学的反馈结果

从表2可以看出，学生对于此次的教学结果是比较满意的，基本认为此次教学对后续学习的帮助很大，而且大部分乐于接受这种将数学史融入数学教学的新方法，希望老师在今后的教学中经常使用该方法。由此可见，此次教学是成功的。

4 总结与反思

此次“无穷级数概念引入”的教学是运用发生方法，在HPM视角下实施的一次教学活动。教学后所实施的学生访谈与问卷调查数据显示，在教学过程中融入数学史有助于学生更好地理解无穷级数的概念以及其敛散性的判别。数学史中生动而有趣的故事激发了学生对于相关概念的浓厚兴趣，进而产生求知的强烈欲望，使得整个教与学的过程环环相扣。