高三数学教学中的“情境脉络一体化”法——以“直线与圆的位置关系(相交)”复习教学设计为例

李太敏 (江苏省灌南县教师发展中心 222500)

数学教学中，利用各种情境进行教学已形成共识.事实上，我们需要的不仅仅是现实的生活情境，更需要知识性问题情境.尤其在高三复习教学中，常见大容量、高密度的习题教学，教师讲得头头是道，学生听得津津有味，但效果有时却大打折扣，甚至学生仍做不出讲过的原题(尤其是难一些的题目).因何如此？其中一个重要的原因就在于教师所讲的问题没有形成问题情境，难以让学生真正内化和同化，特别是题与题之间缺乏情境脉络，无法形成一体化.

本文尝试通过一体化情境的设计，力争说明如何沟通问题与问题之间的联系，从而达到一题带动多题、一法带动多题、个体带动整体的目的．下面以省中小学教学研究第七期课题“新课程背景下中学数学课堂情境有效化实验研究”活动研讨会中，本人所执教的高三研讨课“直线与圆的位置关系(相交)”复习教学设计来加以说明．

1 基本情况

本节的课题为“直线与圆的位置关系(相交)”复习．授课对象为四星级学校高三学生．听课教师来自省教学研究第七期课题“新课程背景下中学数学课堂情境有效化实验研究”的课题组成员，以及市、县部分高三数学教师．

学情分析 活动所在学校虽然是一所四星级学校，但优质生源外流较多，学生基础一般，尤其是计算能力薄弱、解析几何水平一般．

2 教学过程

2.1 引出源问题

源问题情境是一体化设计之本，通过它产生的情境脉络，或串或并，从而形成各种派生问题，可以联通到各个方面．

师：同学们，大家都知道这样一首古诗：

半亩方塘一鉴开，天光云影共徘徊．

问渠那得清如许，为有源头活水来．

这是朱熹的《观书有感》，那么请问，在高三的数学复习课中，教学的源头在哪里？

生：源头是老师．

生：源头是高考题．

生：源头是复习资料．

师：同学们说得都有道理，这是一个仁者见仁的问题，但老师认为高三复习教学的源头在课本教材.这节课我们就通过一道课本习题的演变，来复习“直线与圆的位置关系(相交)”(板书课题)．下面请看苏教版教材必修2第107页的第1题：

源问题过点P(-3,-4)作直线l，当l的斜率为何值时，直线l与圆(x-1)2+(y+2)2=4相交，且所截得弦长为2？

师：下面请同学们用2分钟时间做一下并自行联想、整理、复习直线与圆位置关系的相关知识．

师：哪位同学做好了？请把思路说一下．

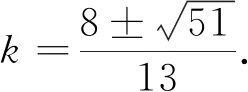
师：说得挺有道理又简洁明了．

生：我要补充，应说明一下斜率不存在时的情况．

生：不需要，因为题中问“当l的斜率为何值时”，说明斜率已肯定存在．

2.2 引出派生题

·类比高考题

师：刚才两位同学的回答合在一起已经很完善了，本题虽不需要讨论，但其他题目的确需要防止遗漏对斜率的讨论，这也需要像这位同学那样做到警钟长鸣．对于这个题目，也许有同学认为小菜一碟，但是2009年江苏高考数学试题解答题第4题就是由这道题发展而来的，其中第(1)问是这样的：

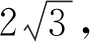
师：在高考中，数学解答题第4题的位置历来具有举足轻重的地位，做得顺利，对考试就有了充分信心，有冲击高分的希望；反之，则会有低分的后果．大家看看这题目，有信心了吧？

生(笑)：有信心．和刚才这道课本题实质一样．

·引出逆命题

师：好的，现在大条件不变，把上面的第(1)问改成：

求证：若直线l1:13x-y+26=0和l2:x+13y-83=0，则直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等．

师：请大家思考一下，然后看谁能说明思路.

生(思考后)：和刚才的课本的那道题方法差不多，只要利用勾股定理，分别求出弦长即可．

师：抓住了问题的本质，能发现这两条直线的位置关系吗？

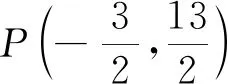
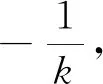
师：说得相当好，也就是说这里的k相当于常数.有谁还要补充的吗？

生：这里应考虑斜率不存在的情况(恍然 大悟)．

说明由于所在学校的学生成绩一般，因此没有直接抛出高考题，而是设立一个梯度进行过渡，先解决高考题的逆命题．

2.3 引出主问题

解析几何中，尤其是关于圆的问题中，常常是以平面几何作为背景，因此利用平几知识来解题有时会比较简单，也体现了方法的优化，同时它也能成为这类问题中的一个共性情境脉胳，也可成为主问题．

·方法的优化

师(提出主问题)：刚才的问题是一个关于圆的问题，除了上述方法外，能用平面几何方法试试吗？在平面几何中，常用什么方法来证明两线段相等呢？(学生思考)

生(思考后)：常用对应的两个三角形全等．分别作出弦心距C1Q1,C2Q2，只要证△Q1PC1≌△Q2PC2．

生(感叹)：这方法简单．

师：解析几何的有些题目本身就是由平面几何演变而来的.刚才这个题目大家已会做了，那么本问题的逆命题，大家能试试吗？

·再现高考题

(2009年江苏卷第18题第(2)问)在平面直角坐标系xOy中，已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4．设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，试求所有满足条件的点P的坐标．

师：能用平面几何方法试试吗？由刚才那个题目,我们能得到什么启示呢？

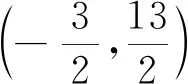
师：在高考中，绝大部分同学所采用的是第一种纯解析几何方法，有些同学虽得出了正确答案，但并不知道问题的来龙去脉；而如若用平面几何方法，则可清楚地看到本题的本质是什么．无独有偶，2008年的江苏卷解几题也同样如此，请同学回去后自已尝试看看．

·类比模拟题

为提高教学的针对性，需把握好例题与练习的问题间的情境脉络，使练习与例题能形成一个整体，形成解题能力突破的组合拳．

师：高考试题如此，而平时的模拟试题又是怎么样的呢？下面请同学们做一个模拟试题：

已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P,Q两点，M是PQ中点，l与直线m:x+3y+6=0相交于N．试探索AM·AN是否与直线l的倾斜角有关.若无关，请求出其值；若有关，请说明理由．

师：本题也可用平面几何解法，能发现吗？能发现直线CA与直线m之间的关系吗？

生(口算后)：垂直．

师：现在再试试．

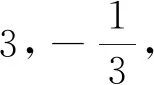
师(小结)：做得好，你发现了本题的本质，也发现了这道题是如何编制的．

一节课很快就要结束了，这节课给同学们留下的最深的一个印象是什么？

生：两种不同方法的比较，尤其是关于圆的问题中，常常是用平面几何的知识来解答更简捷．

师(最后小结)：说得好，的确有些问题的命制就是从平面几何而来的，但我们也不能形成思维定势.吴文俊先生也说：“尽快结束平面几何的教学，尽快引入解析几何的教学.”毕竟考查目的还应是解析几何，在以后的学习中我们会进一步体会到解析几何的作用．今天的课就上到这里，请课后完成有关作业(具体作业略)．

说明通过几道作业题，与教学内容相呼应，进一步强调了本节课所体现的主要理念，尝试比较用平几方法与坐标方法来解决解析几何中的圆问题，从而进一步厘清本节课的情境脉络，形成一体化观念．

3 回顾与反思

3.1 设计立意

由于近年高考数学命题中，很多试题是由课本题引申变化而来，为了使重视课本复习的精神落到实处，这节课的设计立意就是从寻找高三数学教学的源头做起，由课本的原问题，通过它的情境脉络，联想到近年的高考数学试题及其逆命题，再回归到具有共性的平面几何情境的模拟试题.通过一道课本习题的情境脉络及其演变，努力践行一题多解、多解归一、多题归一的高三复习一体化情境教学理念．

美国著名教育心理学家奥苏伯尔曾说：“假如让我把全部教育心理学仅仅归纳为一条原理的话，那么，我将一言以蔽之：影响学习的唯一重要的因素就是学生已经知道了什么；要探明这一点，并应据此进行教学.”考虑到所教的学生基础相对薄弱，因此这节课没有直接抛出较难的高考题，而是进行了多次铺垫，分别将动直线改为定直线、原命题改为逆命题，通过螺旋式上升的设计来贴合学生的最近发展区，让学生既不是很轻松地解决，又能跳一跳够得着．

3.2 设计的原则

(1)遵循了教学背景熟悉化原则

从问题的源头——教材题入手，整个一节课均是对该题进行改编、追问，这样的背景让学生感到很亲切，也乐于学习．

(2)遵循了教学过程活动化原则

课堂教学尽可能让学生处于活动中，力争每一道题都让学生进行尝试，在活动中解决问题.板演的是学生，而多媒体展示的也是学生的成果．

(3)遵循了教学内容思考化原则

思考是数学之魂.在整个的课堂教学中，力争让学生在不停地思考着、体会着．

3.3 设计的关注点

(1)关注题目答案从哪来、到哪去

原始命题的预设解法；教师研讨的多种解答；学生作业中的典型错解与正解．

(2)关注知识点的提取从哪来、到哪去

知识的结构化理解：意在问题解决时提取“连续”.模型的完整构建与再构：意在问题解决时组合“有效”、发展学生模型能力．

(3)关注学生的运算能力从哪来、到哪去

在“慢”中求得运算的正确性：运算能力的强弱体现在正确与迅速上，正确是运算的第一要素，是迅速的基础与前提，要慢慢体会算法、算理、算律.在“快”中提高运算质量：熟能生巧，求“简”中提高运算速度， 求“理”中体会运算规律(为什么这样算，还可怎样算)．

3.4 困惑与思考

如何处理好主问题与次问题的关系：是否需要每个问题都让每个学生的学习“真发生”，是否需要防止过分纠缠于“次问题”中？

如何处理好常规方法与简便方法的关系：是否需要让每个学生都掌握简便的方法，是否需要每题都寻求创新的简便方法？

如何处理好问题简化与深化的关系：是否需要让每个学生都学会将简单问题深化成复杂问题，是否需要每个问题都简化成模型或分解成简单问题？