基于均匀设计及BP神经网络的大体积混凝土热学参数反分析

张玉平，马超，李传习，高树威

(长沙理工大学 土木工程学院，长沙 410114)

大体积混凝土作为现代桥梁的重要组成部分，其开裂问题一直是工程技术人员最为关注的问题之一。为了指导大体积混凝土施工，最大限度降低施工阶段大体积混凝土的开裂风险，可根据现场实际施工状况和现有的温度场理论对其进行有限元分析。但是，在对大体积混凝土温度场和应力场进行有限元分析时，所采用的热学参数主要通过经验公式或试验得到，由于经验公式难免有误差，而试验方法花费高、耗时长而较少使用，并且这些参数在施工期受气象条件、时空、荷载、施工条件等多种因素影响，往往使得所采用的热学参数失真，大体积温控计算偏离甚至严重偏离实际情况，导致一些大体积混凝土结构出现或多或少的裂缝[1-2]，轻则影响结构的耐久性，重则产生工程质量事故，危及人民生命财产安全。因此，准确确定热学参数是大体积混凝土温控能否成功的基础和前提，除试验确定外，通过反演分析确定大体积混凝土的热学参数也是行之有效的方法之一[3]。

目前，对大体积混凝土热学参数的反演分析研究不多。王振红等[4]基于施工现场的混凝土立方体非绝热温升试验，对混凝土热学参数进行了反分析。Amirfakhrian等[5]利用径向基函数来获得内热源反分析的数值解。李守巨等[6]基于模糊理论建立了目标函数，将热传导反问题作为非线性优化问题处理。还有许多学者基于蚁群算法、粒子群算法、遗传算法等优化算法提出热学参数反演方法。但是，其中大部分研究还集中在坝体等水利工程中[7-9]，对桥梁工程中大体积混凝土热学参数反分析较少[10-11]。喻正富等[10]基于施工现场测得的温度数据，采用遗传算法对大体积混凝土的热力学参数进行了反演分析，但在反演过程中采取的是分步反演，而非同步反演。文豪等[11]对遗传算法进行优化改进，提出在MATLAB中调用ANSYS温度场数据，反演得到真实的热学参数，但运用MATLAB调用数据，需另写程序代码，比较繁琐。

为获得混凝土真实的热学参数，笔者将BP神经网络引入到温度场热学参数反分析中，BP神经网络特有的强大非线性映射能力可准确映射各热学参数与温度场之间的复杂非线性关系，结合实测数据即可快速、准确地反演混凝土热学参数。此方法有效避免了采用经验公式求解热学参数时产生的误差，还解决了因试验设备昂贵或试验过程漫长而未及时获取热学参数的问题。并且，在建立神经网络的训练样本时引入均匀设计理论，可在一定程度上减少训练样本，提高效率。研究表明：基于均匀设计及BP神经网络的反分析，得到了能反映大体积混凝土真实性能的多种热学参数，使有限元仿真分析结果能准确地反映实际工程情况，及时采取的相应温控措施避免了温度裂缝的产生。

1 均匀设计与BP神经网络的基本原理

1.1 均匀设计理论

均匀设计又称均匀设计试验法，是基于试验点在整个试验范围内均匀散布的，从均匀性角度出发提出的一种试验设计方法[12]，由方开泰教授和数学家王元在1978年共同提出。均匀设计表一般用符号Un(qs)表示，其中U表示均匀表，n表示试验次数，q表示因素水平数，s表示最多可安排的因素数。其中，n=q，s=q-1，即均匀设计表的试验次数n等于水平数q，最多可安排的因素数比水平数少1，而正交设计表中试验次数n等于水平数q的平方，相比于正交设计试验，均匀设计试验可大大减少试验次数。例如，某试验有6个因素，每个因素取31个水平，其全部组合有316=887 503 681，若用正交设计至少需要312=961次试验，而用均匀设计只需31次试验，由此可见，均匀设计较正交设计更适用于多因素多水平试验。

均匀试验设计还具有一个鲜明的特点，即能从全面试验点中挑选出部分代表性的试验点，保证每个因素的每个水平做且仅做一次试验。例如，做2因素11水平的试验，应选用U11(1110)表，表中共有10列，最多可安排10个因素，现在有2个因素，根据U11(1110)的使用表，应取1、7列安排试验，如图1所示。当有4个因素时，应取1、2、5、7列安排试验。笔者采用均匀设计理论确定热学参数样本，在保持样本均匀性不变的前提下，可大幅提高计算效率。

图1 两因素均匀设计布点图Fig.1 Two-factor uniform design

1.2 BP神经网络的基本原理

BP(Back Propagation)神经网络[13]是目前应用最广泛的一种前馈型神经网络模型。在函数逼近、模式识别、分类问题、数据压缩等领域均有广泛应用。BP神经网络由信息的正向传播和误差的反向传播两个过程组成。正向传播中，输入层接收外界信息并向隐含层传播，隐含层负责信息变换，最终传至输出层。当实际输出与期望输出不符时，进入误差的反向传播阶段。反向传递中，按误差梯度下降的方式逐层反传至隐含层、输入层，直到预测输出无限逼近期望输出。BP神经网络结构一般由输入层、一个以上的隐含层、输出层组成。理论证明，3层的BP神经网络(单隐含层)可以实现从输入到输出的任意非线性映射。由图2可见，若输入层有m个神经元，输出层有n个神经元，则可实现m维至n维的映射。

图2 单隐含层BP神经网络映射结构图Fig.2 Single hidden layer BP neural network mapping

BP神经网络最大的优点就是可以避免函数的具体形式，不必像显式函数那样需要提前确定定义域和值域，所以，在工程领域多应用于岩石力学中的岩石行为预测[14]、边坡位移反分析[15]等问题中。混凝土热学参数反分析同边坡位移反分析一样，均是复杂的非线性问题，难以用显式的函数来描述，而这种复杂的非线性问题可以通过BP神经网络得到较好的映射。

2 BP神经网络反演分析方法

2.1 概述

反分析问题的求解方式一般分为解析反分析法和数值反分析法[16]。解析反分析法主要是通过找出现场监测值与待反演参数之间的显式关系，建立数学模型，进而求得待反演参数。但是，由于实际工程问题的复杂多变性，一般难以确定其数学模型，显式函数关系亦很难建立。因此，针对上述问题，有研究人员提出，建立反分析问题的目标函数，将参数求解问题转化为目标函数最优解问题[17]，采用有限元法等数值方法进行迭代计算，并逐步修正待反参数，直至函数寻到最优解。但当反演参数比较多时操作起来将非常费时，因为寻优过程需要反复迭代，且对复杂问题搜索到最优解的概率较低。BP神经网络为反分析问题提供了一条有效的途径。其一，BP神经网络由其特有的拓扑结构来表述反分析中的复杂非线性问题，无需建立数学模型；其二，BP神经网络解决问题时，只需事先提供训练样本，完成训练即可，无需反复迭代。

2.2 大体积混凝土温度场影响因素分析

在温度场分析中，主要热学参数包括：混凝土的比热c、密度ρ、导温系数α、导热系数λ、绝热温升θ0以及常数m。上述参数中混凝土的比热c、密度ρ可直接测得，计算精度可满足计算要求。绝热温升θ0受到水泥品种、用量、骨料粒径以及实验室环境与施工环境差异等多种因素的影响，如果不通过试验确定就应进行反分析；导热系数λ受混凝土密实性、材料特性以及骨料岩性的影响，难以确定，应予以反演。导热系数λ=αcρ，因此，只需反演λ、α任意一个参数即可；水泥水化热计算表达式主要有指数式、双曲线式、复合指数式3种[1]。计算所用的水化热表达式采用指数式函数θ(t)=θ0(1-e-mt)，其常数m随水泥品种、比表面及浇筑温度不同而不同，更能体现施工现场实际浇筑环境，也确保所选表达式与有限元分析软件热源函数的定义保持一致。除绝热温升θ0外，还应对常数m进行反演。因此，选取绝热温升θ0、常数m、导热系数λ作为反演参数，根据相关文献，确定取值范围见表1。

表1 待反演热学参数及取值范围Table 1 Inversion of thermal parameters and the range of their values

2.3 反分析步骤

基于均匀设计及BP神经网络热学参数反分析步骤如图3所示。

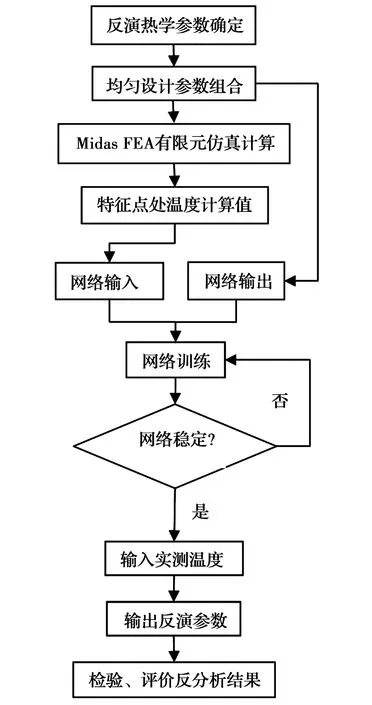
图3 反分析流程图

3 算例分析

3.1 工程概况

太洪长江大桥是主跨为808 m的钢箱梁悬索桥，桥梁全长为1 436 m，为重庆南川至两江新区高速公路NL5标段控制性工程。大桥南岸锚碇为隧道式锚碇，隧道锚混凝土施工包括后锚室、锚塞体、前锚室以及散索鞍支墩承台，隧道锚立面布置见图4。散索鞍支墩承台分左右两幅，每幅尺寸为15 m(长) ×13 m(宽)×6 m(高)，混凝土浇筑总量约2 340 m3，是典型的大体积混凝土结构。支墩承台分3层浇筑，每层浇筑厚度均为2 m，见图5。采用C40混凝土，混凝土设计配合比的材料用量如表2所示。

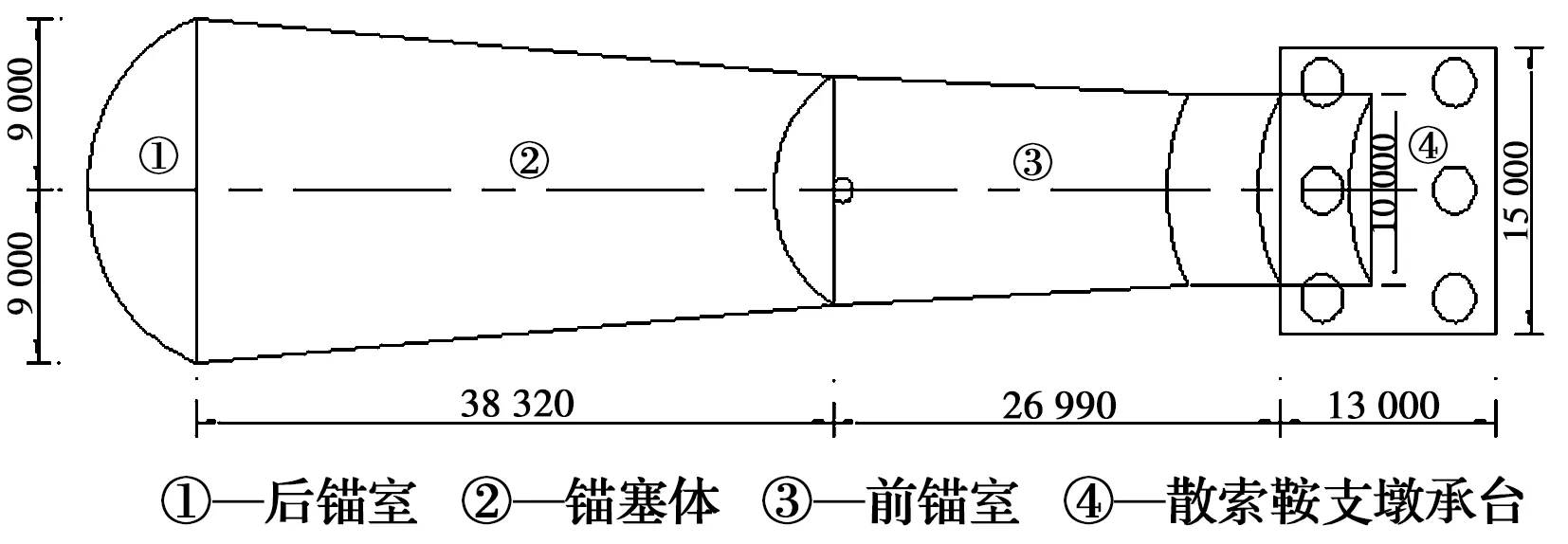
图4 隧道锚结构分布图(单位：mm)Fig.4 The structure distribution of tunnel

图5 散索鞍支墩承台分层示意图(单位：mm)Fig.5 Layered schematic diagram of splay saddle pier

表2 每m3混凝土设计配合比材料用量

3.2 温度测点布置及监测方法

考虑到结构的对称性和温度的变化规律，选取1/4结构进行温度测点布置，测点布置如图6所示[18]。采用实时无线温度综合测试系统进行监测，可根据需要设置温度采集频率，温度监测频率为2 h采集一次。太洪长江大桥南岸散索鞍支墩承台于2019年3月18日21：00开始浇筑，3月19日19：00浇筑完成，浇筑历时22 h，测得混凝土入模温度为16.9 ℃。为获得真实的桥址环境，环境温度从混凝土开盘前一星期开始监测，在施工现场的背阴处布置测点，把实测环境温度输入有限元模型，排除昼夜温差干扰。温度曲线如图7所示。

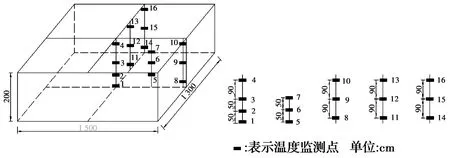
图6 支墩承台每层温度监测点布置图Fig.6 Arrangement diagram of temperature monitoring points of each layer of pier

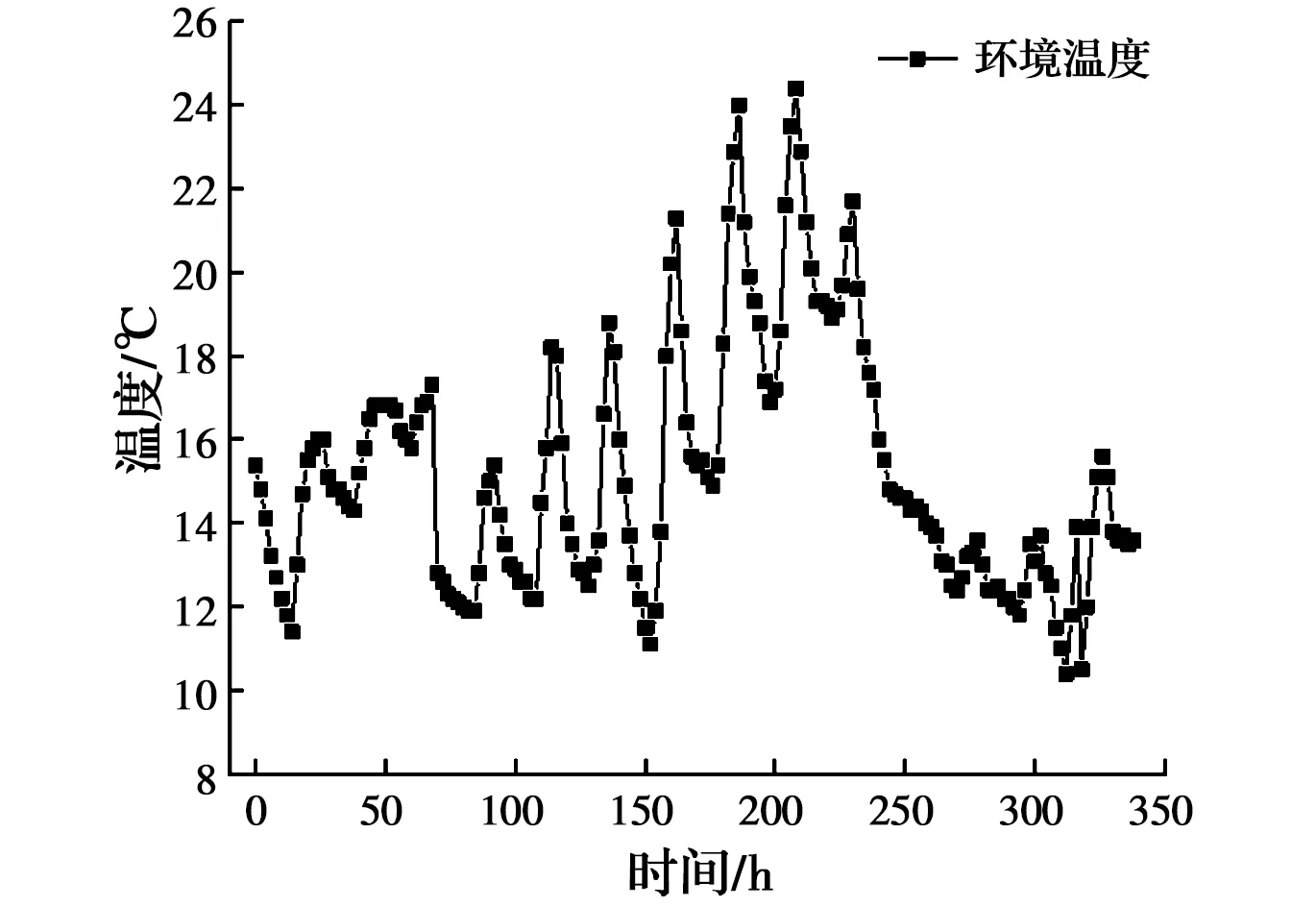
图7 2019年3月11日—26日环境温度曲线图Fig.7 Environmental temperature curve from March 11-26,

3.3 有限元模型

采用通用有限元软件 Midas FEA 建立有限元模型，共有87 035个单元，16 848个节点。如图8所示。模型考虑基岩对混凝土水化热的吸收作用，建立地基扩大模型，固定温度取为20 ℃，基岩侧面和底面给予固定约束。根据现场实际的施工过程，分为3个施工阶段，即2 m一层。混凝土抗压强度通过试验确定，根据对试拌混凝土的各项技术指标检测及抗压强度试验,得到7、28 d抗压强度分别为44.2、49.7 MPa。

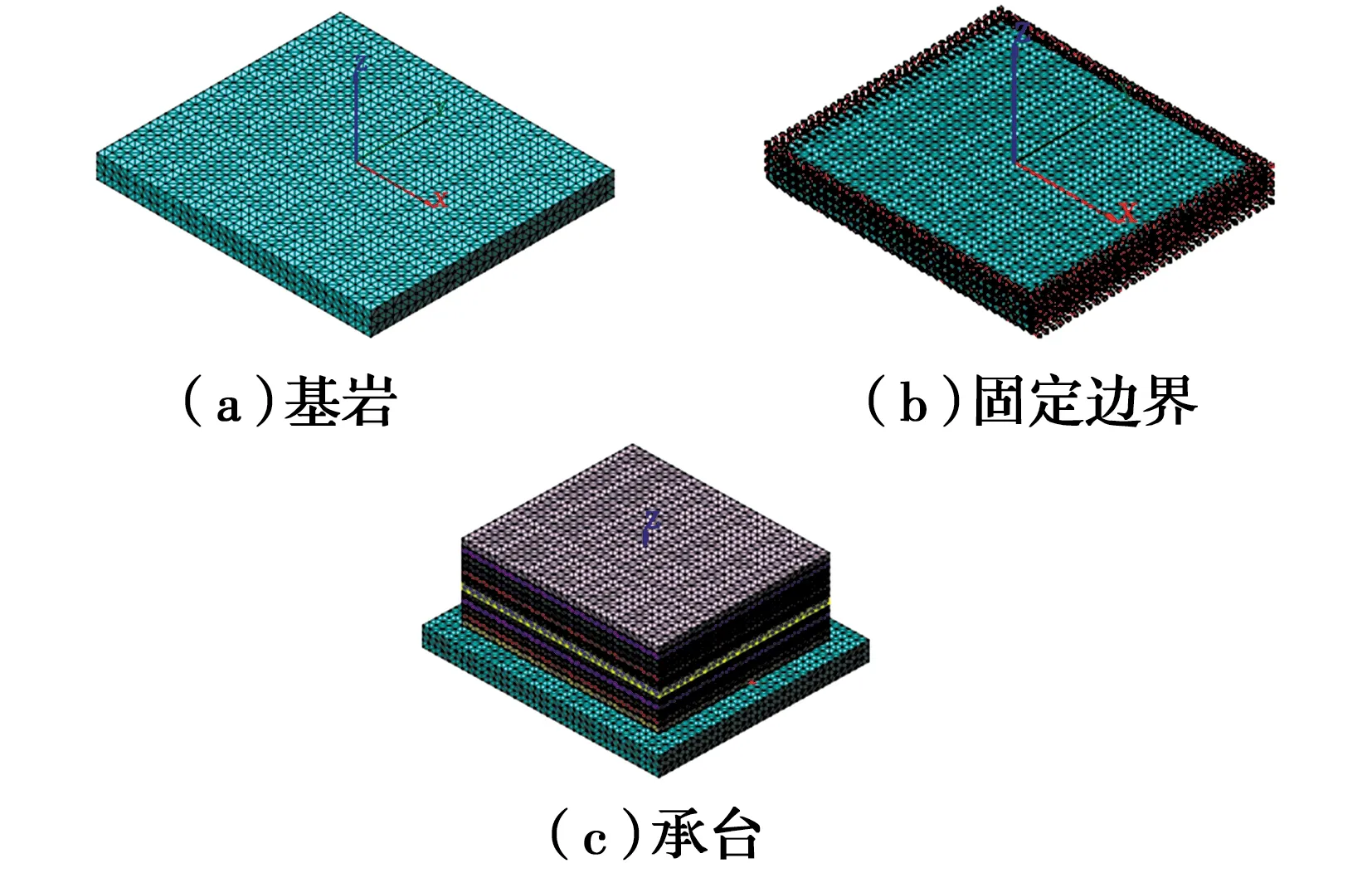
图8 支墩承台有限元模型Fig.8 Finite element model of pier bearing

3.4 BP神经网络的建立

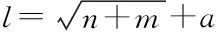
3.4.2 样本设计及数据归一化处理 采用均匀设计方法确定参数样本，参数的水平数取为31，选取均匀设计表为U31(3110)，样本值见表3。将表3的参数样本数据输入有限元计算模型，得到支墩承台特征点的温度计算值，见表4。

表3 参数设计样本值表Table 3 The samples of thermal parameters design

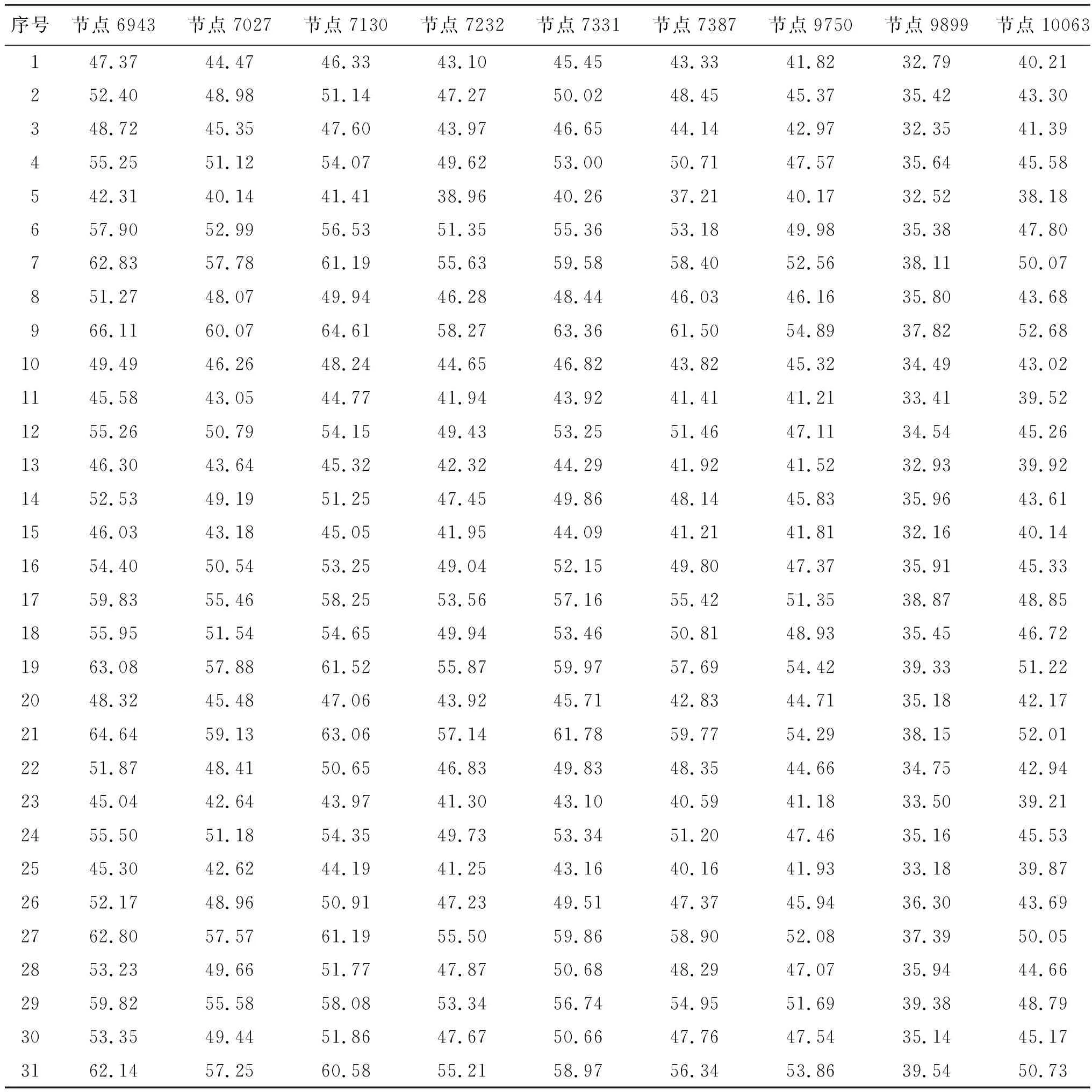
表4 特征点温度计算值

考虑到各参数之间的量纲影响以及小数值信息被大数值信息淹没现象的发生，在处理输入与输出数据时，要用到归一化方法。神经网络模型采用tan-sigmod型传递函数，该函数的值域为[-1, 1]，因此，在计算过程中用式(1)预处理数据，通过实际样本试算，使其全部归一化到[-1, 1]区间内，归一化公式为

(1)

以导热系数λ为例计算该组数据归一化后的值。

(2)

以此类推，求得导热系数归一化后的值为

λ=[-0.332 -0.4 … 0.4 0.332]

(3)

归一化用MATLAB语言实现。

[input_train,inputps]=mapminmax(P1)；

[output_train,outputps]=mapminmax(T1)；

其中:input_train和output_train为归一化返回的值，结构体inputps和outputps是进行归一化时所用的参数。

3.4.3 网络训练及效果评估 为了提高网络训练速度，使学习时间更短，同时保证训练过程的稳定性，采用附加动量法对神经网络进行优化，附加动量法是在每个加权调节量上加上一项正比例于前次加权变化量的值，使网络在修正其权值时不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响，在没有附加动量的作用下，网络可能陷入浅的局部极小值，利用附加动量可以带动梯度下降过程，冲过狭窄的局部极小值，从而提高训练速度。具体表达为

(4)

式中：Δω(t)=ω(t)-ω(t-1)；α为动量因子，一般取值0.95。

在网络训练前还需对一部分参数期望值先进行设置。网络最大训练次数设置为1 000次，训练期望精度设置为1×10-4。网络误差梯度目标值设为默认值0，网络训练过程中，误差梯度实际值约为0.004 76，与目标值0接近，认为误差梯度符合要求。神经网络训练过程中，为了防止网络的过度训练而使泛化能力降低，设置有终止训练功能的有效性检查步数，即确认样本的误差曲线不再下降的连续迭代次数，在网络训练之前，对有效性检查步数的值进行不同设定后分别进行试验，最终确定为6。训练过程误差曲线见图9，可以看出，优化后的训练过程随着训练次数的递增稳定收敛，比优化前更快、更早收敛。BP神经网络训练过程结果具有随机性，为评估网络训练效果是否达到预期，用12组归一化后的数据多次反演来检验测试样本训练效果，以平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为误差评价指标。

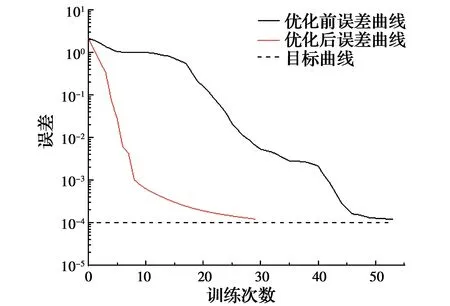
图9 训练过程优化前后误差曲线对比图Fig.9 Comparison of error curves before and after

(5)

(6)

式中：observes为预测值；predicted为设计值；亦称真实值；N是样本数。平均绝对百分比误差又可称为相对误差的绝对值平均值，由于离差被绝对值化，不会出现正负相抵消的情况，因此，更能反映训练效果的可信程度。与相对误差类似，它是一个百分比值，即如果MAPE值为5，则表示预测值较真实值平均偏离5%。均方根误差是用来衡量观测值同真实值之间的偏差，RMSE值越小，表示精度越高。每次训练的平均绝对百分比误差、均方根误差见表5，第1次训练的热学参数设计值与预测值的趋势见图10，可以看出：平均绝对百分比误差均小于10%，均方根误差值均小于1.2，预测值与设计值拟合度较高，说明神经网络模型对大体积混凝土预测精度较高，可以用来反演大体积混凝土热学参数。

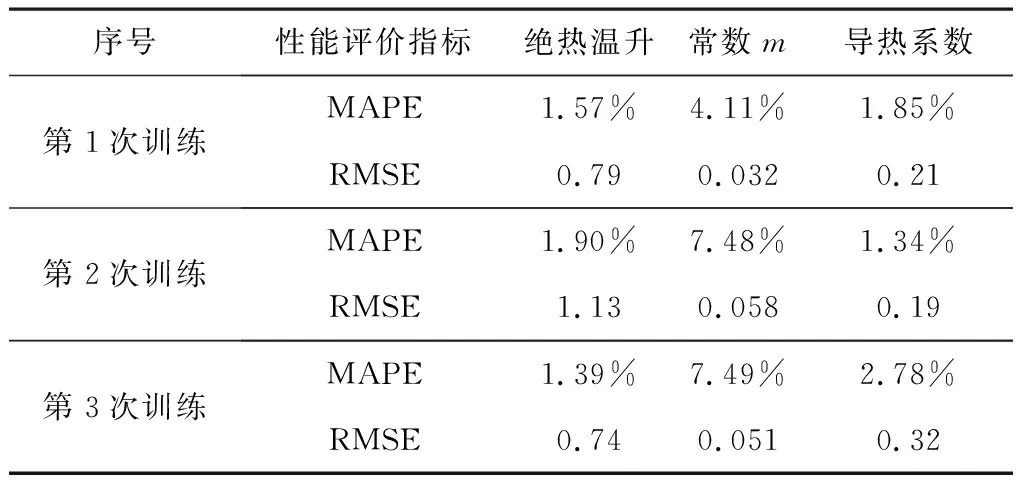
表5 各热学参数平均绝对百分比误差与均方根误差Table 5 MAPE and RMSE of each thermal parameter

3.5 反演分析结果与检验

将特征点实测温度值输入网络，输出即为3个热学参数的反演值，见表6。反分析完成后，还需对热学参数反演值进行检验，具体方法是，将反演值输入有限元模型，计算出第2个施工阶段特征点处温度计算值，并与该施工阶段测得的实际温度值进行比较，检验二者的拟合程度，计算温度值与实测温度值拟合曲线如图11～图14所示。由图可知，温度计算值与实测值之间的误差较小，变化规律基本一致，表明基于BP神经网络反演得到的热学参数符合混凝土的实际施工环境，该组反演值真实可靠。

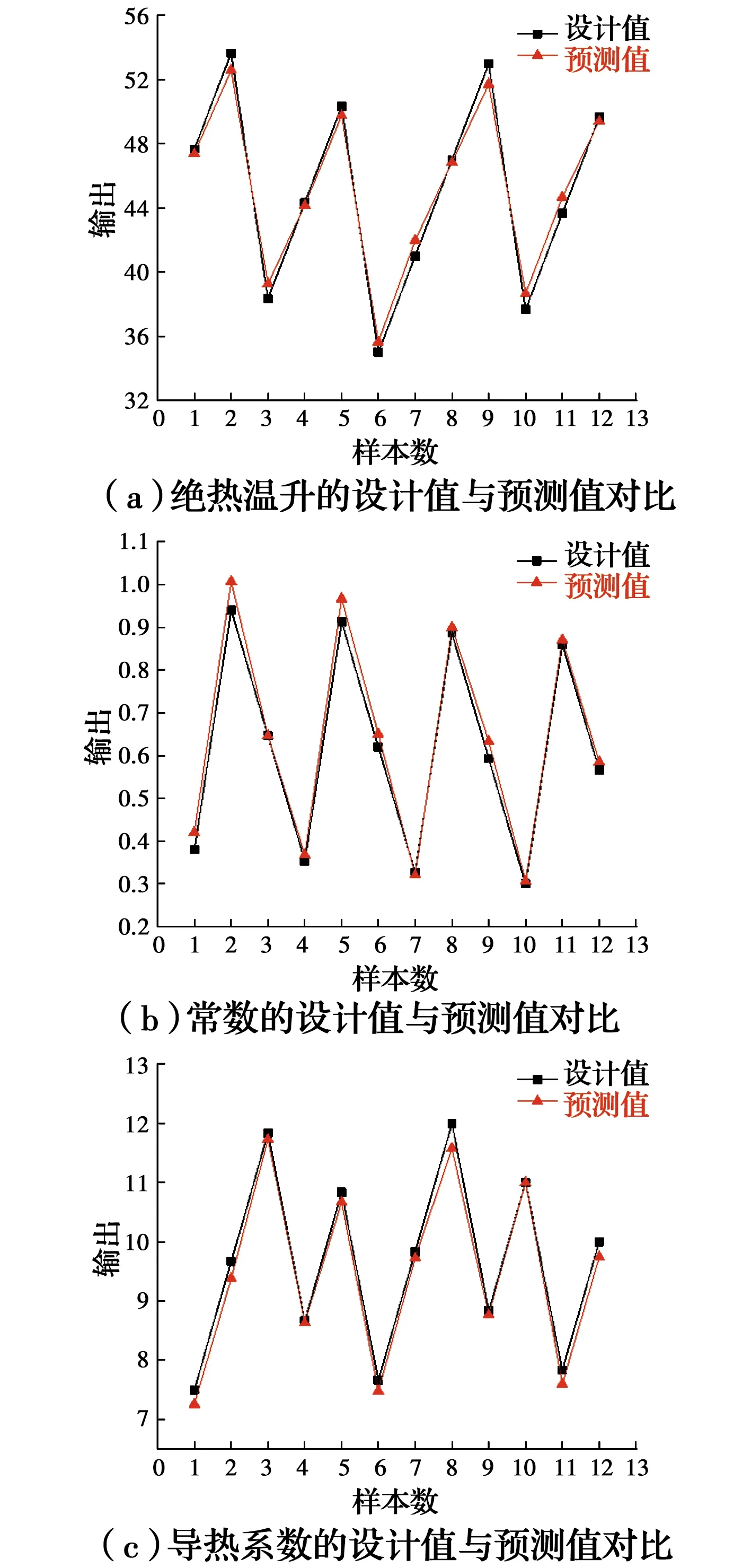
图10 12组测试样本各参数设计值与预测值对比Fig.10 Comparison of design values and predicted values of each parameter in 12 test

表6 参数反演分析结果Table 6 The result of back analysis

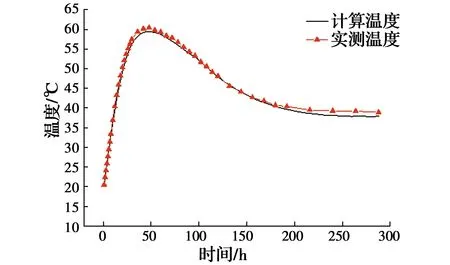
图11 C2-2温度计算值与实测值对比曲线Fig.11 Comparison curve of calculated values and measured

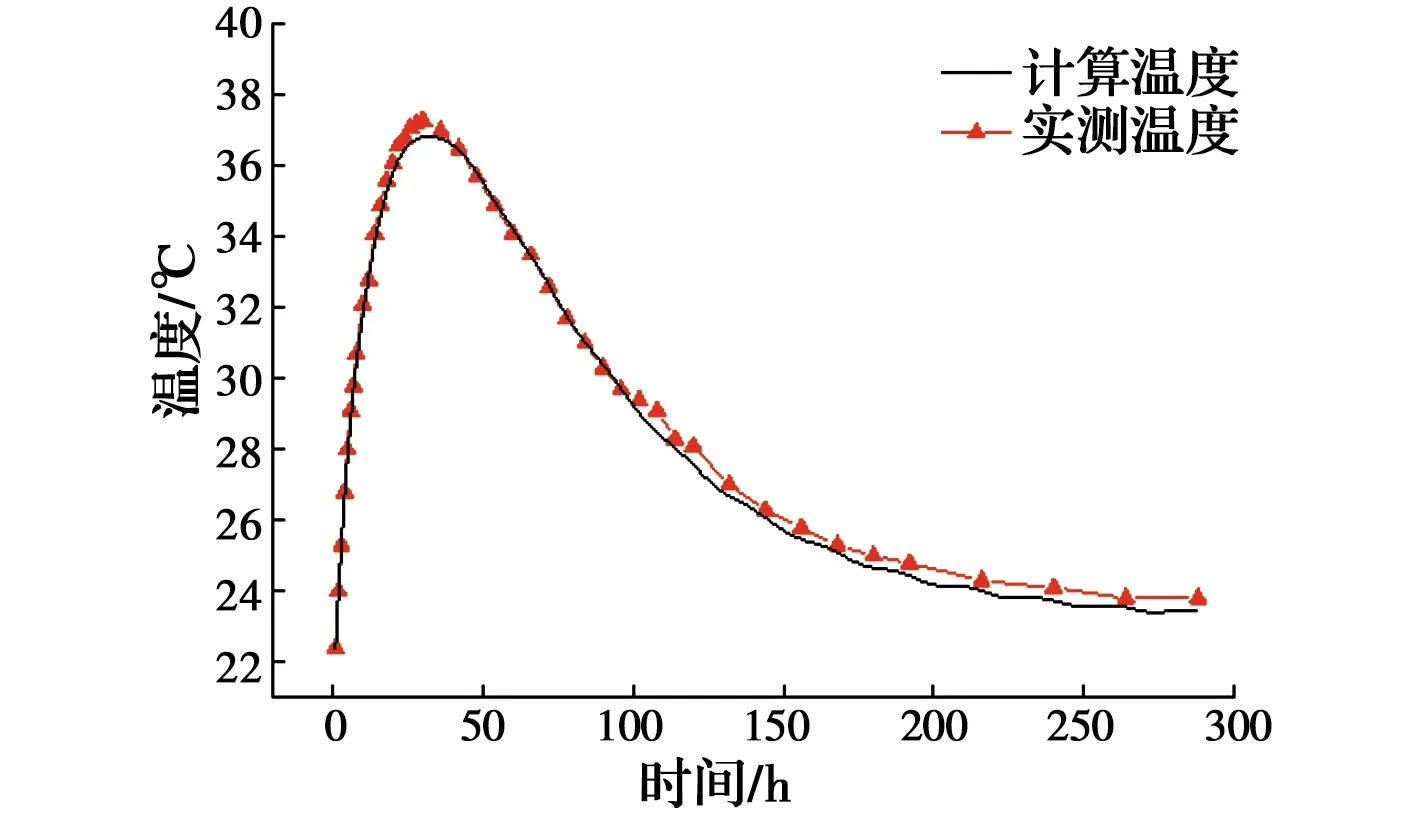
图12 C2-4温度计算值与实测值对比曲线Fig.12 Comparison curve of calculated values and measured

图13 C2-7温度计算值与实测值对比曲线Fig.13 Comparison curve of calculated values and measured

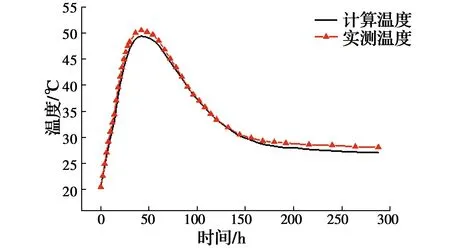
图14 C2-9温度计算值与实测值对比曲线Fig.14 Comparison curve of calculated values and measured

4 结论

以太洪长江大桥散索鞍支墩承台为工程背景，为得到混凝土真实的热学参数，基于均匀设计和 BP神经网络对大体积混凝土绝热温升、反应速率、导热系数等热学参数进行反演，揭示了温度场与热学参数之间的内在联系和规律，得到如下结论：

1)施工期大体积混凝土的温度峰值与混凝土热学参数之间的复杂非线性关系可由BP神经网络表述完成，运用BP神经网络可避免主观调整热学参数所造成的误差，有较强的实用性。

2)在BP神经网络训练阶段，采用附加动量法优化网络结构能明显减少网络训练时间，提高训练效率。

3)利用均匀设计和BP神经网络相结合的反分析方法，可以大大减少网络学习的样本数量。同时，可使有限元正分析与反分析过程分离，大大减少了反分析时间，提高了反分析效率和准确性。

4)通过BP神经网络反分析得到的大体积混凝土热学参数分别为：绝热温升θ0=46.834 2 ℃，常数m=0.979 504，导热系数λ=9.742 07 kJ/(m·h·℃)，结合有限元正分析对后续施工的混凝土温度场进行预测，得到的特征点温度计算值与温度实测值较为接近，在变化规律上基本吻合，温度峰值最大误差仅为1.1 ℃，表明基于均匀设计及BP神经网络方法可较准确地反演大体积混凝土热学参数。