隧道开挖引起水平向位移被动桩的简化计算方法
冯国辉,窦炳珺,张高锋,丁士龙,徐长节,4
(1.浙江大学 滨海和城市岩土工程研究中心,杭州 310058;2.浙江省大成建设集团有限公司,杭州 310012;3.浙江杭海城际铁路有限公司,浙江 嘉兴 310020;4.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室;江西省地下空间技术开发工程研究中心,南昌 330013)
盾构隧道开挖过程中会造成周边地层的变形,这极有可能威胁到邻近桩基的正常工作。准确预测盾构隧道开挖对邻近桩基的影响已成为目前地下工程领域的一大研究热点。
目前,已有很多学者对盾构隧道开挖引起邻近桩基的影响进行了深入研究。分析方法主要分为3类:第1类室内试验方法,Xiang等[1]利用透明土和PIV技术研究了隧道施工对周边土体的影响,并得到土体位移的实测数据;周东等[2]利用透明土和PIV技术和光学测量系统设计了被动桩在侧向位移作用下桩周土体测量的试验方法,得到了桩基在不同埋置深度下桩周土体的位移场。第2类是利用大型商业有限元软件来模拟盾构开挖对邻近桩基的影响,有限元适用范围广,但使用较为复杂,需要准确地确定土层参数及边界条件才能获得较满意的结果[3-4]。第3类是理论解析法,理论解析是基于经典弹性力学,在考虑桩端边界条件基础上进行严格的理论推导。目前最主要的方法都是采用两阶段分析法:第1阶段分析盾构隧道开挖引起桩基所在轴线处土体位移;第2阶段将轴线处土体位移直接加到桩基上,再采用合理的模型模拟桩-土相互作用,求解出桩基变形的解析解。理论分析法相比于实验和有限元法物理意义明确,能够精准地计算盾构隧道开挖引起的邻近桩基变形。第1阶段中, Loganathan等[5]提出了能够准确预测盾构开挖引起地层位移的三维计算公式,因具其有良好的计算精度而被广泛应用。李早等[6]、熊巨华等[7]基于Winkler地基梁模型并结合桩基两端约束情况,采用有限差分法研究了盾构隧道开挖引起的邻近桩基竖向位移及内力;梁发云等[8]基于Winkler地基模型,利用最小势能原理建立被动桩变分控制方程,随后解得被动桩位移及其内力;上官士青等[9]在研究邻近堆载时,考虑到桩土水平位移不一致的情况,提出水平方向双位移刚度矩阵,并通过多个算例验证了其正确性。由于Winkler地基模型计算简单,在工程领域得到广泛的应用,但其表达式中忽略了土体的剪切变形,使得计算值与实际结果存在较大的误差,为了克服这一缺点,Pasternak等[10]提出了具有考虑土体剪切变形的Pasternak地基模型,由于Pasternak地基模型的精确度较高而被广泛地应用于地下工程研究中[11-12]。梁发云等[13]基于Pasternak地基模型分析得到水平受荷被动桩的位移和内力;Zhang等[14]将桩基简化成Pasternak地基模型且考虑到桩土三维空间情况下盾构隧道开挖引起邻近桩基的变形响应,验证了考虑桩土三维空间作用能更精确地预测桩基变形。为了更加准确预测桩土相互作用的内力和变形,Kerr等[15]提出三参数Kerr地基模型,相比于Winkler地基模型和Pasternak地基模型,Kerr地基模型更具优越性,也有少数学者将其用于地下工程研究中[16-17]。
笔者在前人研究的基础上,采用两阶段分析法,分析在盾构开挖作用下邻近桩基的受力变形规律。基于Loganathan等(1998年)的修正后解析公式得到盾构开挖作用下桩基水平附加应力;采用Kerr三参数地基模型建立被动桩的水平位移控制微分方程,合理地提出了剪切层弯矩的假设,利用有限差分数值计算方法得到桩基水平位移控制方程的数学解析矩阵表达式,通过与实例分析对比验证所提计算方法的有效性,并通过不同地基模型所得结果的比对说明三参数地基模型的优越性;最后,深入分析了隧道直径、桩基直径、桩隧中心线水平和竖向间距对桩基水平位移的影响。
1 Kerr地基模型下桩基简化计算方法
1.1 单桩水平反应分析
Kerr地基模型相比Pasternak地基模型增加了一个可变的弹性变形参数,能更准确地预测地基变形,如图1所示。基于Kerr地基模型,做出以下假设:
1)假设桩基为一根直径为d,刚度为EI的纵向圆形截面Euler-Bernoulli梁。
2)地基模型由k、G、c这3个参数组成,其中,剪切层不产生压缩变形。
3)桩基与土体紧密接触,其变形和土体变形协调一致。
4)不考虑桩基与土体之间的摩擦。

图1 Kerr地基下桩土相互作用模型Fig.1 Pile-soil interaction in Kerr foundation
假设作用在桩基上的荷载为p,在该荷载作用下,桩基挠度w为
w(z)=w1(z)+w2(z)
(1)
式中:w1为左侧弹簧的变形量;w2为剪切层变形量,假设桩基以及剪切层左侧的应力分别为
q1(z)=cw1=c(w-w2)
(2)
q2(z)=kw2
(3)
对于剪切层,有
(4)
通过式(2)和(4),可得
(5)
桩基平衡方程为
(6)
将式(4)、式(5)带入式(6),可得Kerr地基模型下不考虑桩土相互作用的控制方程
(7)
式中:w2代表下层弹簧的水平位移;p代表作用在桩基上的附加应力;d和EI分别代表桩基圆形截面的半径和抗弯刚度;k、c分别代表上层弹簧和下层弹簧的地基反力, 参照简化弹性空间法[18]取c=3k;G为剪切层刚度,且k、G满足
(8)
式中:ES为土体弹性模量;t为土体剪切层厚度,根据相关文献[19],取t=11d。如图2,利用差分法可将式(7)差分为
A(w2)i+B(w2)i-3+C(w2)i-1+D(w2)i+
C(w2)i+1+B(w2)i+3+A(w2)i+3=-pi
(9)
式中:i=0,1,2,…,(n-1),n。由差分法知
(10)
(11)
(12)
(13)
(14)
(15)
(16)
式中:W=c+k;l=L/n,L为桩基竖向长度;pi为桩基附加应力,可表示为
(17)
式中:z为地表以下深度,Ux(z)为盾构施工引起的土体水平自由位移场,可以用Loganathan等给出的公式进行计算
(18)
式中:ν为土体泊松比;R为隧道半径;H为隧道轴线深度;x0为桩基到隧道中心线的水平距离;ε0为等效地层损失比。
结合桩基边界条件,得到单桩位移方程为
{w2}=[K]-1·{-pi}
(19)
式中:
(20)

图2 桩体差分示意图Fig.2 Differential diagram of
当桩基两端为自由的摩擦桩时,单桩两端的剪力和弯矩均为0,且满足剪切层弯矩也为0,即
(21)
式中:MS0和MSn分别为桩基两端剪切层的弯矩;M0和Mn分别为桩基两端弯矩;Q0和Qn分别为桩基两端剪力。那么[K]为
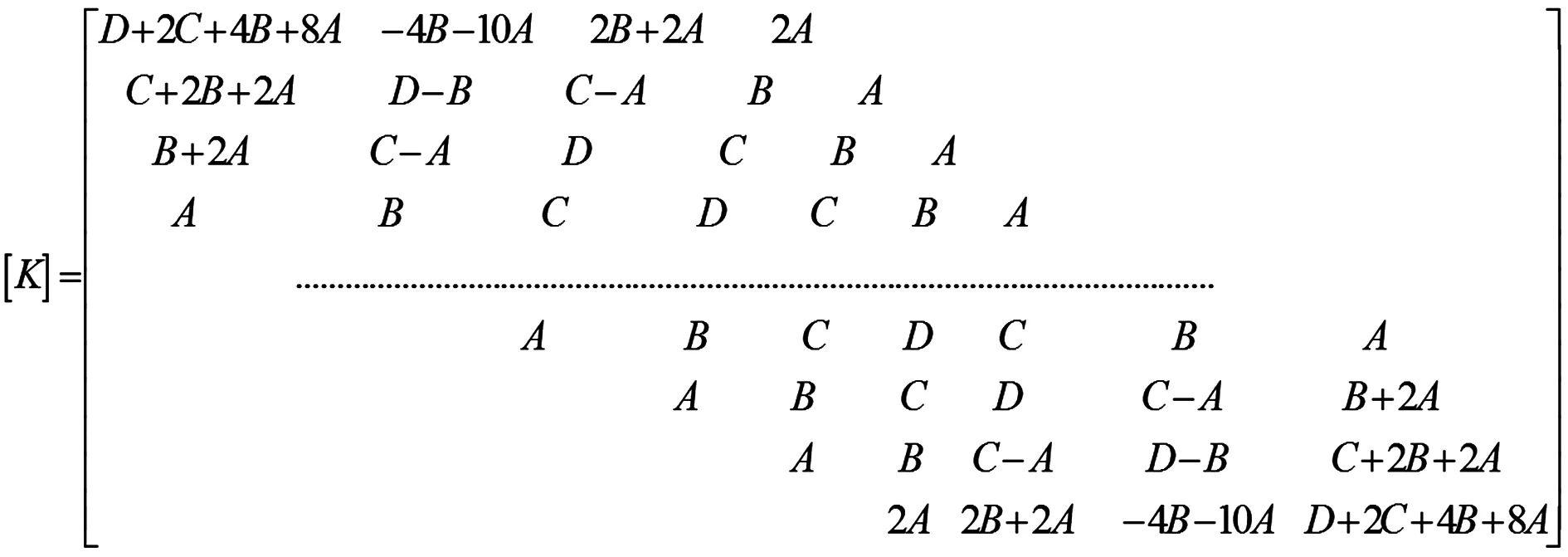
(22)
1.2 群桩水平位移分析
考虑到群桩中桩基对邻近桩基的遮蔽效应使得桩基实际位移相对于其单桩时有所减少。在群桩基础中,单个桩基的实际位移应该等于单桩位移和群桩遮蔽位移之和,其中,遮蔽位移与单桩自由位移方向相反。
邻近群桩简化模型如图3所示。假设桩1土体自由位移为Ux1(z),桩1水平实际位移为δ11,那么由于遮蔽效应在桩1处产生的遮蔽位移为
Δδ1(z)=δ11(z)-Ux1(z)
(23)
式中:Ux1(z)为隧道施工在桩1位置处产生的土体自由位移。
那么简化计算桩1的遮蔽效应引起的桩2的遮蔽位移Ux21(z)为
Ux21(z)=λ(s,z)·Δδ1(z)=λ(s,z)·{δ11(z)-Ux(z)}
(24)
式中:λ(s,z)为水平向土体传递系数。
(25)
式中:Ux2(z)为隧道施工在桩2位置处产生的土体自由位移。
Kerr地基模型下,在桩1影响下,桩2的水平位移控制方程为
(26)
式中:δ21为桩1的遮拦作用引起桩2的水平遮拦位移;Ux21为由于桩1的遮拦效应在桩2处产生的土体水平遮蔽位移。因此,在图3中,桩2的实际水平位移一方面是由于隧道开挖引起土体位移产生的桩2附加水平位移,此过程可通过控制方程(7)得出δ22,另一方面是桩1引起的遮蔽位移,此过程可通过控制方程(26)得出δ21,即
(27)
1.3 不同地基模型比较
将本文方法与常用的单参数和双参数地基梁模型进行比对,即分别选取Winkler、Pasternak地基上桩基受荷平衡微分方程
(28)
(29)
参数选取原则同Kerr地基梁模型,具体计算见式(8)。3种不同地基模型计算所得的桩基挠曲变形曲线与实测数据对比见下节的算例分析。
2 算例分析
2.1 单桩实测验证
以杭州在建地铁侧穿既有桥梁桩基工程为例,设计组根据实际情况,选择隧道下穿邻近既有桩基,具体设计如图4所示。

图4 盾构开挖与桥梁桩基的位置示意图Fig.4 Location diagram of shield excavation and
取最靠近隧道中心线的桩1进行分析,桩长15 m,钻孔灌注桩模量EP=30 GPa,桩截面为圆形,直径1 m;隧道直径7.7 m,隧道中心线距离地面H=20.18 m,隧道中心线到桩1最近水平距离x=4.96 m,竖向距离y=5.18 m,地层损失为ε0=1%,根据勘测数据可知,土体泊松比v=0.27。地层分布由上到下依次为杂填土、素填土、卵石、全风化粉砂岩、强风化粉砂岩、中风化粉砂岩,层状分布,对于不同土层的土体模量采取加权平均法进行计算,得到土体模量ES=22 MPa。将桥梁桩基视为Euler-Bernoulli梁搁置在不同的地基模型上,分别得到不同地基模型下桩基的水平位移与实测数据的对比,如图5所示。
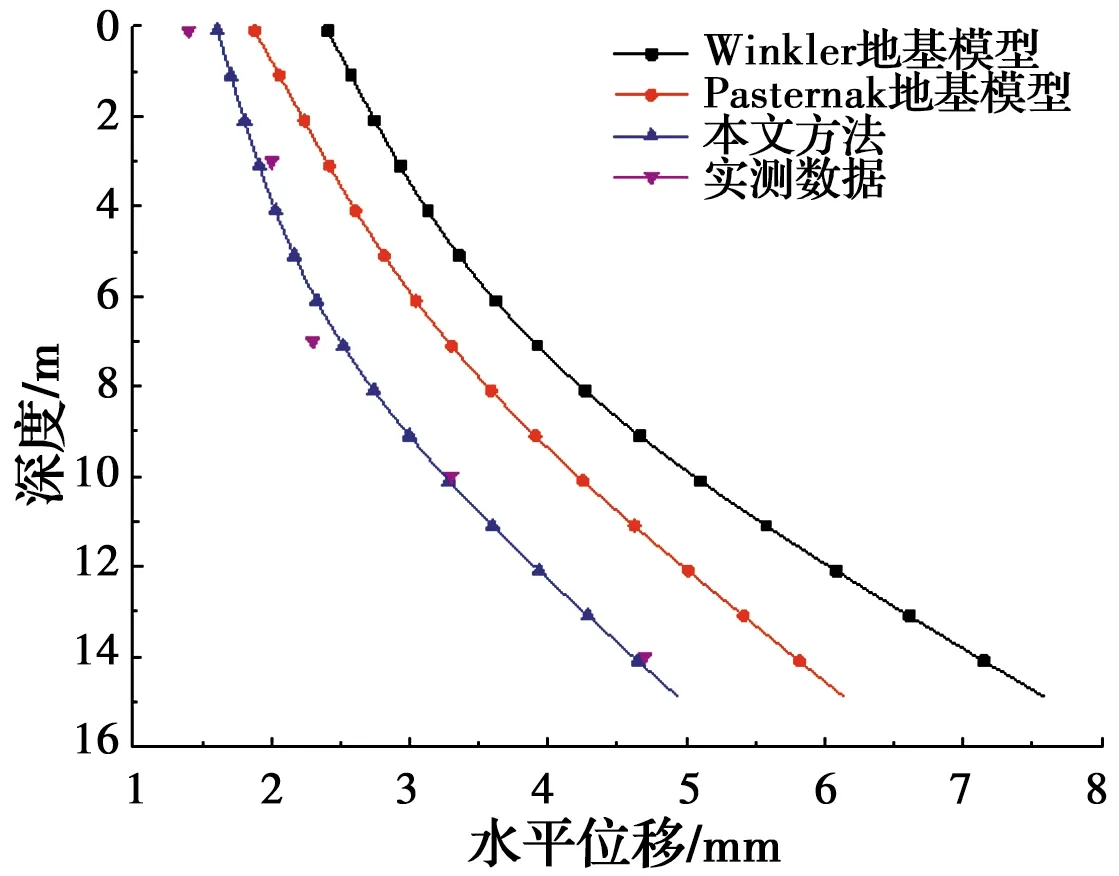
图5 桥梁桩基水平位移计算及实测数据曲线Fig.5 Horizontal displacement calculation and measured data curve of bridge pile
由图5可以看出,相比于Pasternak地基模型和Winkler地基模型,本文模型更加接近于实测数据,这是由于Winkler地基由于没有考虑剪切层的影响,其结果与Kerr地基的结果差别较大。Pasternak模型较Winkler模型更为接近Kerr模型,但结果差别仍较大,说明第3个参数c的加入使得Kerr模型的结果更加准确。
2.2 群桩实测验证
以浙江省某邻近高铁基桩的城市地铁盾构工程为例[20],设计组在盾构隧道和高铁基桩之间建立一道隔离桩来保护邻近的高铁基桩,根据本文方法假定高铁基桩和和隔离桩桩两端均自由,具体设计如图6所示。
由于中间两个基桩有互相遮蔽位移的影响,最左侧桩基受到的附加应力最大,本算例取4个邻近高铁基桩中最左侧的桩基进行研究,如图7所示。根据文献[20]可知其工程参数,见表1,其中,隔离桩与高铁基桩均为圆形截面,高铁桩桩长35 m,取高铁桩有效桩长也为15 m(高铁基桩离地面超过15 m时,其基桩水平位移较小,可不考虑)。
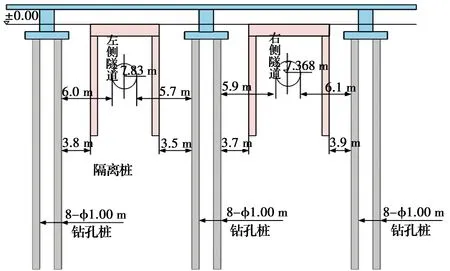
图6 盾构开挖与实际桩基位置示意图Fig.6 Location diagram of shield excavation and

表1 桩-隧平面计算参数Table 1 Calculation parameters of pile-tunnel plane

图7 隧道与群桩简化示意图Fig.7 Simplified schematic diagram of tunnel and pile
如图8所示,由文献[21]可知,当桩中心距小于3倍桩径时,堆卸载导致的土体侧向位移在被动桩附近产生的侧压力90%以上的份额均由被动桩承担,由此可知,本文中的隔离桩可等效成地下连续墙[22],等效公式为
(30)
式中:D为桩的直径;t1为两桩的净距;h为等效厚度。经计算,隔离桩等效厚度为0.62 m。

图8 隔离桩平面布置示意图Fig.8 Layout diagram of isolation
将隔离桩和高铁基桩视为Euler-bernoulli梁搁置在不同的地基模型上,分别得到不同地基模型下高铁基桩的水平位移与实测数据的对比,如图9所示。

图9 高铁基桩水平位移计算及实测数据曲线Fig.9 Horizontal displacement calculation and measured data curve of pile under high-speed
由图9可以看出,相比于Pasternak地基模型和Winkler地基模型,本文模型更加接近于实测数据,3条曲线的发展趋势一致,但Winkler地基模型仅考虑了土体之间的弹簧作用,计算得到的数据偏大,Pasternak在Winkler地基模型上考虑了土体的剪切作用,使得计算结果得到进一步优化,本文方法在Pasternak地基模型基础上增加了可调节的弹簧系数c,使得计算结果更加精确,更加满足实际工程数据。
3 参数分析
为了研究桩基直径、隧道直径、桩隧相对位置对桩基受力变形的影响,以杭州在建地铁侧穿既有桥梁桩基工程为例,其中x=y=5 m,其余参数不变。在研究某一参数对桩土相互作用的影响时,其余参数不变。
3.1 不同桩径对桩基水平位移的影响
为了研究桩基受力变形与桩基直径之间的关系,取5组不同的桩基直径进行分析,分别为d=0.8、1.0、1.2、1.4、1.6 m,并采用本文方法计算桩基水平位移。
由图10可以看出,随着桩基深度的增加,桩身位移增加的趋势没有发生改变,但随着桩基桩径的增大,桩身水平位移增加的速率在逐渐减小,这是由于随着桩径的增大,桩基的刚度EI也逐渐增大,桩基的抗变形能力增强,造成桩身水平位移增速减小,故在工程实践中,适度增大桩径可以有效地控制开挖对邻近桩基水平位移的影响。
3.2 不同隧道直径对桩基水平位移的影响
为了研究桩基受力变形与隧道直径之间的关系,取5组不同的隧道直径进行分析,分别为R=0.8、1.0、1.2、1.4、1.6 m,并采用本文方法计算桩基水平位移。
由图11可以看出,随着隧道半径的增大,桩基的水平位移也逐渐增大,且增大的速率也越来越明显,这是由于隧道直径的增大直接导致开挖隧道过程中地层应力产生较大改变,桩周土的附加应力快速变化,使得桩基水平位移增大且增速有加快的趋势,故在工程实践中要尽可能地减小隧道开挖直径。

图10 不同桩径下桩基水平位移变化图Fig.10 Variation diagram of horizontal displacement of pile foundation under different pile
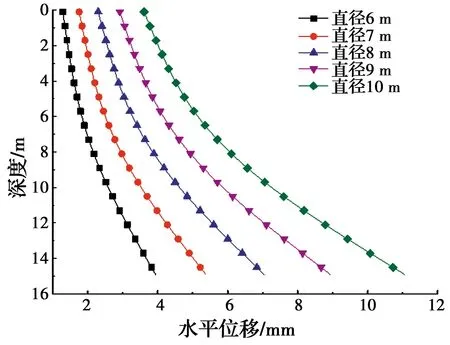
图11 不同隧道直径下桩基水平位移变化图Fig.11 Variation diagram of horizontal displacement of pile foundation under different diameters of the
3.3 不同桩隧间距对桩基水平位移的影响
为了研究桩基受力变形与桩基和盾构开挖的水平距离和竖向净距之间的关系,取多组不同的数据进行分析,令水平距离x=5 m不变,y/x=1、1.2、1.4、1.6、1.8,令y=5 m,x/y=1、1.2、1.4、1.6、1.8,采用本文方法计算这两种情况下桩基水平位移并比较两种不同情况对桩基水平位移的影响,如图12所示。
由图12可以看出,随着x或者y的增大,桩基水平位移均会减小。这是由于随着隧道中心线远离桩基位置,隧道开挖在桩周产生的附加应力也会相应地减小,但对于桩底以下的隧道开挖过程,x、y增大相同的比例时,增大竖向距离y更能减小桩基的水平位移,这也符合实际工程中土体是成层分布的情况。一般来说,增大竖向位移会使隧道穿越更下层弹性模量更大的土层,隧道开挖产生的卸载应力在土体传递的过程中能够充分消减,从而起到保护邻近桩基的作用,此种工况下,应尽可能地增大隧道埋深以减小对邻近桩基的影响。
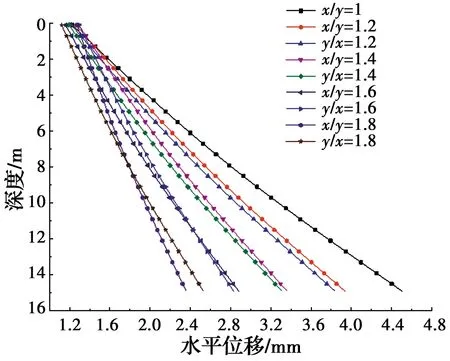
图12 不同x、y比值下桩基水平位移变化Fig.12 Variation diagram of horizontal displacement of pile foundation under different ratio of x to
4 结论
1)采用两阶段分析法,基于Loganathan求得隧道开挖卸荷作用下桩基水平附加应力;采用Kerr三参数地基模型建立被动桩的挠曲微分方程,提出了剪切层弯矩的假设,并利用有限差分数值计算方法推导出其数学解析矩阵表达式。
2)将本文结果与两个工程实例及不同地基模型进行对比。分析结果表明,Winkler地基由于没有考虑剪切层的影响,故其结果与Kerr模型结果差别较大。Pasternak模型较Winkler模型更为接近Kerr模型,但计算结果仍然没有Kerr模型接近实测数据,两个案例均说明Kerr地基模型相较其他模型更为准确。
3)在单桩分析过程中,增大桩基的直径能减小桩基水平位移,但效果不明显;增大隧道直径会增大邻近桩基的水平位移,且增大速率随着隧道直径增大有加速的趋势。
4)对于隧道开挖在桩底以下的情况,相对于增大隧道中心线与桩基的水平距离,增大隧道的埋深更能减小邻近桩基的水平位移。

